【深度学习】S2 数学基础 P4 概率论
目录
- 基本概率论
- 概率论公理
- 随机变量
- 多个随机变量
- 联合概率
- 条件概率
- 贝叶斯定理
- 求和法则
- 独立性
- 期望与方差
- 小结
基本概率论
机器学习本质上,就是做出预测。而概率论提供了一种量化和表达不确定性水平的方法,可以帮助我们量化对某个结果的确定性程度。
在一个简单的图像分类任务中;
- 如果我们非常确定图像中的对象是一只猫,那么我们可以说标签为 “猫” 的概率是 1,即 P ( y = “猫” ) = 1 P(y =“猫”) = 1 P(y=“猫”)=1;
- 如果我们无法区分图像是猫还是狗,那么我们可以说两者出现的概率相等,即 P ( y = “猫” ) = P ( y = “狗” ) = 0.5 P(y =“猫”) = P(y =“狗”) = 0.5 P(y=“猫”)=P(y=“狗”)=0.5;
- 如果我们对图像是否为猫不太确定,我们可以将概率设置在一个介于 0.5 和 1 之间的值,表示我们对其为猫的确定性程度不是完全的,但比完全不确定要高。
这种概率的量化和比较使得我们可以更加客观和量化地评估和处理不确定性。
概率论公理
概率论名词:
- 样本空间:所有可能结果的集合;
- 事件:给定样本空间的一个子集;
- 概率:将集合映射到真实值的函数,反映了事件发生的可能性;
概率论公理:
- 对于任意事件,其概率从不会是负数;
- 整个样本空间的概率为 1;
- 对于互斥事件(A、B、C互斥),有 P ( A ∪ B ∪ C ) = P ( A ) + P ( B ) + P ( C ) P(A∪B∪C)=P(A) + P(B) + P(C) P(A∪B∪C)=P(A)+P(B)+P(C);
随机变量
随机变量是将样本空间中的每个结果映射到一个实数集上的函数;
e . g . e.g. e.g. 以掷一个六面的骰子为例,其样本空间 S S S 包含所有可能的结果,即 S = { 1 , 2 , 3 , 4 , 5 , 6 } S = \{1, 2, 3, 4, 5, 6\} S={1,2,3,4,5,6}。我们定义一个随机变量 X X X,它将每个结果映射到一个实数。这里假设我们设定 X = x 2 + 1 X = x^2+1 X=x2+1,其中 x x x 为骰子的结果。
那么我们可以计算出每个结果对应的 X X X 值:
- 当 x = 1 x=1 x=1 时, X = x 2 + 1 = 2 X = x^2+1=2 X=x2+1=2;
- 当 x = 2 x=2 x=2 时, X = x 2 + 1 = 5 X = x^2+1=5 X=x2+1=5;
- 当 x = 3 x=3 x=3 时, X = x 2 + 1 = 10 X = x^2+1=10 X=x2+1=10;
- 当 x = 4 x=4 x=4 时, X = x 2 + 1 = 17 X = x^2+1=17 X=x2+1=17;
- 当 x = 5 x=5 x=5 时, X = x 2 + 1 = 26 X = x^2+1=26 X=x2+1=26;
- 当 x = 6 x=6 x=6 时, X = x 2 + 1 = 37 X = x^2+1=37 X=x2+1=37;
因此,离散随机变量 X X X 的可能取值为 {2, 5, 10, 17, 26, 37};在公平骰子的情况下,每个结果出现的概率是相等的,出现的概率都为 1 6 \frac 1 6 61。
多个随机变量
联合概率
联合概率 P ( A = a , B = b ) P(A=a, B=b) P(A=a,B=b) 描述的是事件 A A A 发生且事件 B B B 也发生的概率。具体来说,它表示在所有可能的情况中,事件 A A A 结果为 a a a 且事件 B B B 结果为 b b b 的这种情况出现的概率是多少。
隐含在这个概念中的概率定律是,事件 A A A 和事件 B B B 同时发生的概率不会超过事件 A A A 或者事件 B B B 单独发生的概率。即 P ( A = a , B = b ) ≤ P ( A = a ) P(A=a, B=b) ≤ P(A=a) P(A=a,B=b)≤P(A=a)。
条件概率
而联合概率不等式的变形:
0 ≤ P ( A = a , B = b ) P ( A = a ) ≤ 1 0 ≤ \frac {P(A=a, B=b)} {P(A=a)} ≤ 1 0≤P(A=a)P(A=a,B=b)≤1
这个比率称为条件概率,并用 P ( B = b ∣ A = a ) P(B=b|A=a) P(B=b∣A=a) 来表示。他是 B = b B=b B=b 的概率,前提是 A = a A=a A=a 已发生。
完整公式为: P ( B ∣ A ) = P ( A B ) P ( A ) P(B|A)=\frac {P(AB)} {P(A)} P(B∣A)=P(A)P(AB)
贝叶斯定理
根据条件概率的定义,我们可以得出统计学最有用的方程之一:Bayes 贝叶斯定理。
P ( A ∣ B ) = P ( B ∣ A ) ⋅ P ( A ) P ( B ) P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)⋅P(A)
贝叶斯定理的直观含义是,当我们观察到事件 B B B 发生时,事件 A A A 发生的概率会根据事件 B B B 发生的概率和对事件 A A A 和 B B B 相关性的了解而改变。贝叶斯定理是一种强大的工具,可以帮助我们在有新的证据出现时更新我们对某个假设的信念。
求和法则
根据求和法则, P ( B ) = ∑ A P ( A , B ) P(B)=\sum_{A}P(A,B) P(B)=A∑P(A,B)
B B B 的概率相当于计算 A A A 的所有可能选择,并将所有选择联合概率聚合在一起。
独立性
如果两个随机变量 A A A 和 B B B 是独立的,意味着事件 A A A 的发生跟事件 B B B 的发生无关。根据贝叶斯定理,马上就能得到 P ( A ∣ B ) = P ( A ) P(A|B)=P(A) P(A∣B)=P(A);
独立性的一个常见例子是抛硬币。抛掷一枚公平的硬币,事件 A A A 是出现正面,事件 B B B 是出现反面。因为硬币的每一面出现都是相互独立的,所以事件 A A A 发生不影响事件 B B B 发生的概率,反之亦然。因此,事件 A 和事件 B 是独立的。
独立性在统计学和概率论中非常有用,它简化了我们对事件之间关系的理解。如果我们知道两个事件是独立的,那么我们就可以将它们的概率分开来考虑,而不需要考虑它们之间的任何关系。
期望与方差
期望描述了一个随机变量在多次重复实验中平均可能取得的值。
E x P [ f ( x ) ] = ∑ x f ( x ) P ( x ) E_{x~P}[f(x)]=\sum _x f(x)P(x) Ex P[f(x)]=x∑f(x)P(x)
方差衡量的是随机变量分布中采样不同的 x x x 值时,函数值偏离该函数的期望的程度。
V a r [ f ( x ) ] = E [ ( f ( x ) − E [ f ( x ) ] ) 2 ] Var[f(x)]=E[(f(x)-E[f(x)])^2] Var[f(x)]=E[(f(x)−E[f(x)])2]
小结
- 我们可以从概率分布中采样;
- 我们可以使用联合分布、条件分布、Bayes 定理、边缘化和独立性假设等来分析多个随机变量;
- 期望和方差为概率分布的关键特征的概括提供了实用的度量形式。
以上
本节概率论内容全部为理论知识。实践部分将在后续博文中逐步展现。
2024.2.15
相关文章:

【深度学习】S2 数学基础 P4 概率论
目录 基本概率论概率论公理随机变量 多个随机变量联合概率条件概率贝叶斯定理求和法则独立性 期望与方差小结 基本概率论 机器学习本质上,就是做出预测。而概率论提供了一种量化和表达不确定性水平的方法,可以帮助我们量化对某个结果的确定性程度。 在…...

跟我学c++中级篇——静态多态
一、多态 Polymorphism,多态。学习过c的人如果不知道多态,基本上就是打入c内部的C程序员了。在前边曾经对多态进行过分析,对其中的虚函数(虚表等)也进行过较为详细的说明。 多态其实非常好理解,不要硬扣书…...
)
设计模式--桥接模式(Bridge Pattern)
桥接模式(Bridge Pattern)是一种结构型设计模式,它主要是用于将抽象部分与实现部分分离,使它们可以独立地变化。 桥接模式主要包含以下几个角色: Abstraction(抽象类):定义抽象类的…...
统计图饼图绘制方法(C语言)
统计图饼图绘制方法(C语言) 常用的统计图有条形图、柱形图、折线图、曲线图、饼图、环形图、扇形图。 前几类图比较容易绘制,饼图绘制较难。今值此介绍饼图的绘制方法。 本方法采用C语言的最基本功能: ( 1.)…...

洛谷C++简单题小练习day12—寻找最小值小程序
day12--寻找最小值--2.16 习题概述 题目描述 给出 n 和 n 个整数 ai,求这 n 个整数中最小值是什么。 输入格式 第一行输入一个正整数 n,表示数字个数。 第二行输入 n 个非负整数,表示 1,2…a1,a2…an,以空格隔开。 …...

相机图像质量研究(13)常见问题总结:光学结构对成像的影响--鬼影
系列文章目录 相机图像质量研究(1)Camera成像流程介绍 相机图像质量研究(2)ISP专用平台调优介绍 相机图像质量研究(3)图像质量测试介绍 相机图像质量研究(4)常见问题总结:光学结构对成像的影响--焦距 相机图像质量研究(5)常见问题总结:光学结构对成…...
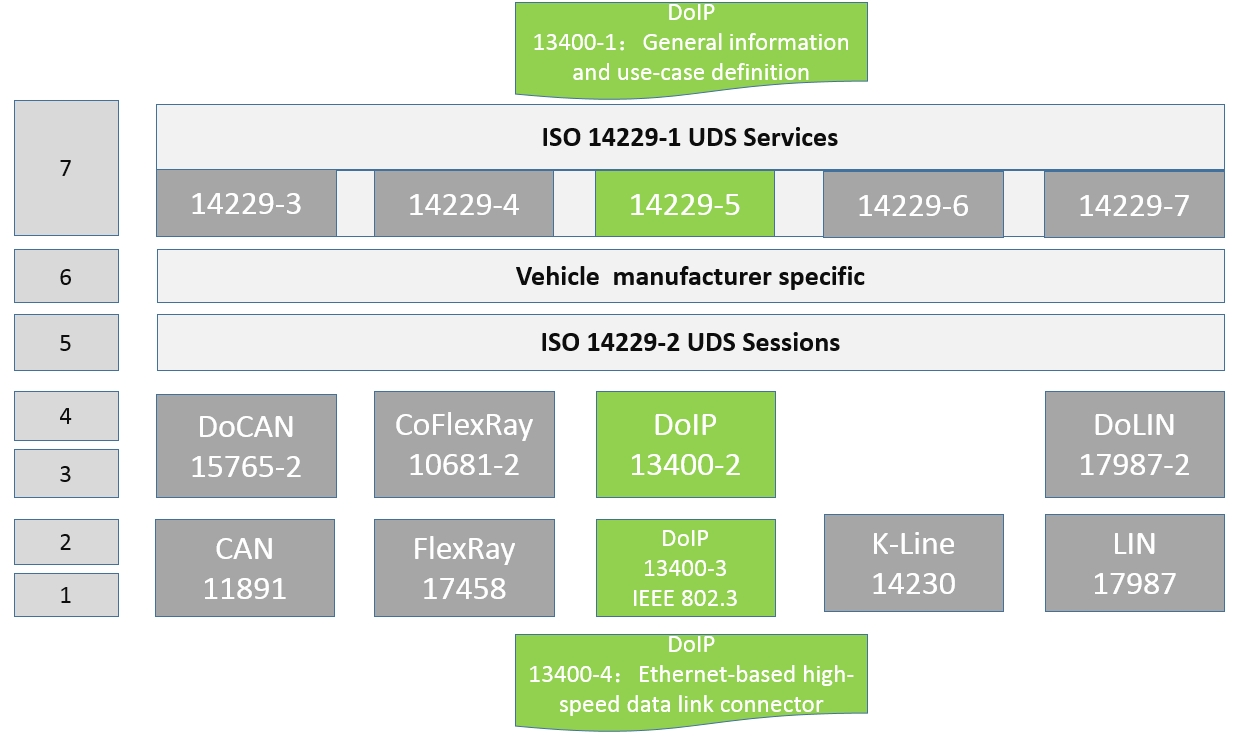
车载诊断协议DoIP系列 —— 车辆以太网节点需求汇总
车载诊断协议DoIP系列 —— 车辆以太网节点需求汇总 我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师(Wechat:gongkenan2013)。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 本就是小人物,输了就是输了,不要在意别人怎么看自己。江湖一碗茶,…...

掘根宝典之C++包含对象的类,私有继承,保护继承,三大继承方式总结
包含对象成员的类 包含,组合和层次化:一个类里面的类成员之一是个类对象 我们来看个例子 #include<iostream> using namespace std; class AA { private:int a_; public:AA(int a):a_(a){}void A(){cout << a_ << endl;} }; class …...

第六篇:MySQL图形化管理工具
经过前五篇的学习,对于数据库这门技术的理解,我们已经在心中建立了一个城堡大致的雏形,通过命令行窗口(cmd)快速上手了【SQL语法-DDL-数据定义语言】等相关命令 道阻且长,数据库技术这一宝藏中还有数不清的…...

计算机网络——12DNS
DNS DNS的必要性 IP地址标识主机、路由器但IP地址不好记忆,不便于人类用使用(没有意义)人类一般倾向于使用一些有意义的字符串来标识Internet上的设备存在着“字符串”——IP地址的转换的必要性人类用户提供要访问机器的“字符串”名称由DN…...
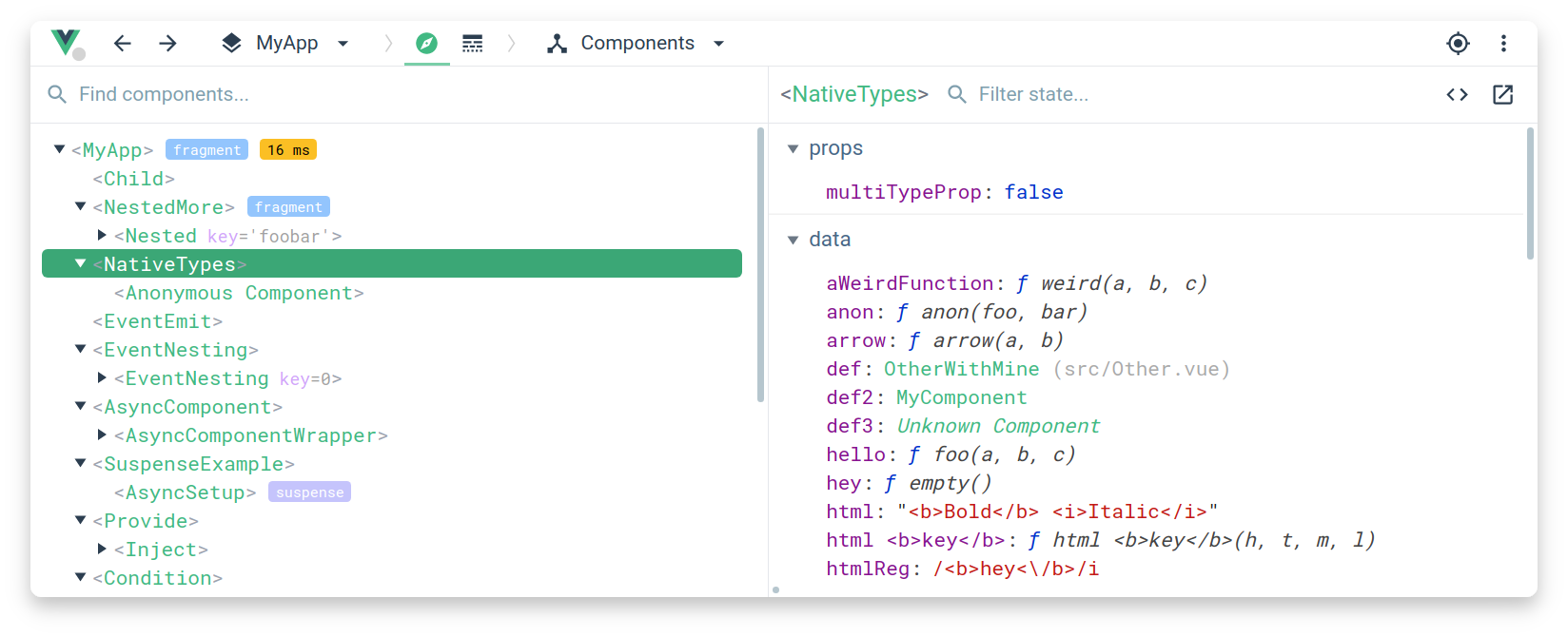
vue3-应用规模化-工具链
工具链 项目脚手架 Vite Vite 是一个轻量级的、速度极快的构建工具,对 Vue SFC 提供第一优先级支持。作者是尤雨溪,同时也是 Vue 的作者! 要使用 Vite 来创建一个 Vue 项目,非常简单: (推荐)…...
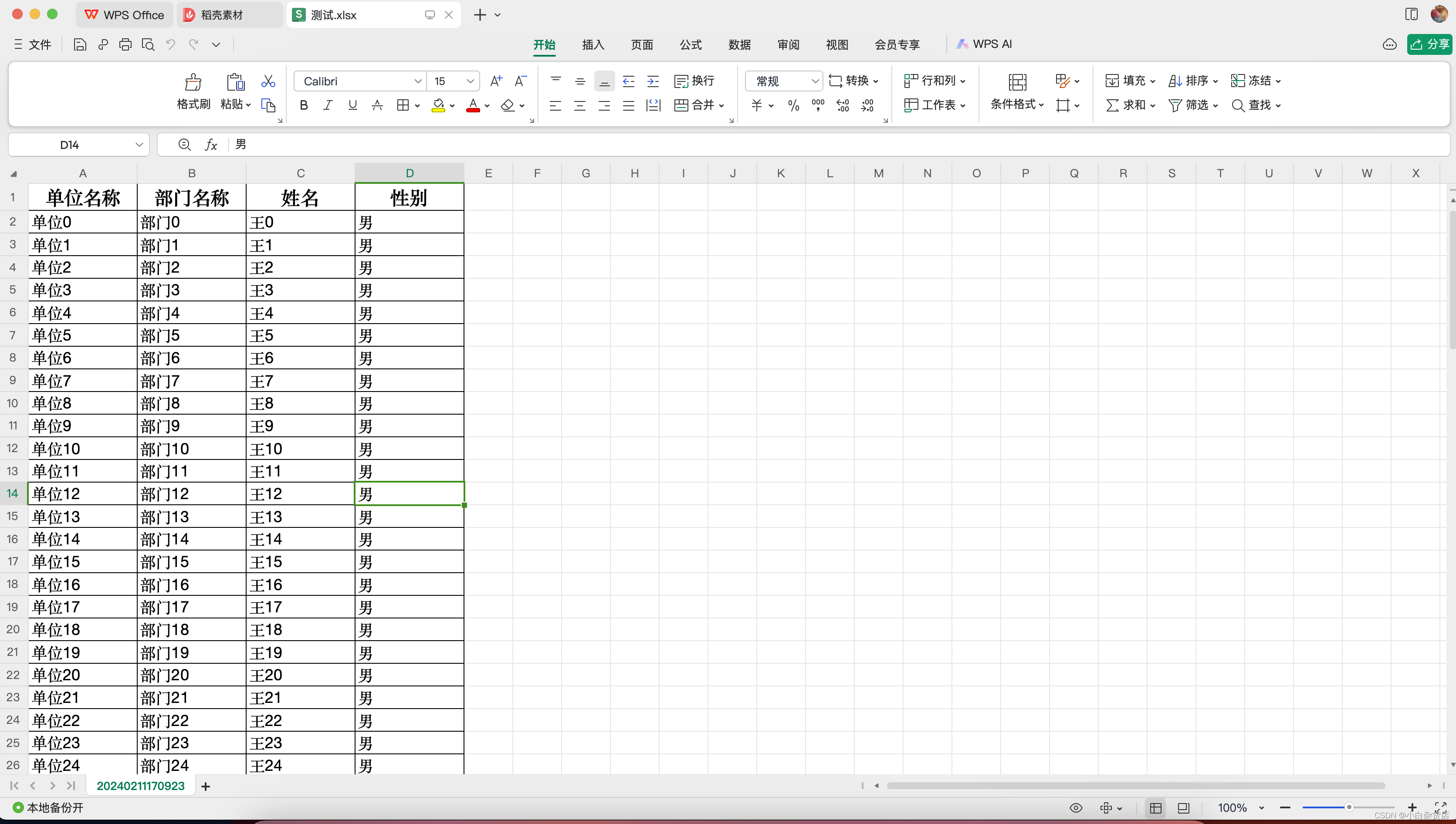
EasyExcel动态列导出
测试代码地址:https://gitee.com/wangtianwen1996/cento-practice/tree/master/src/test/java/com/xiaobai/easyexcel/dynamiccolumn 官方文档:https://easyexcel.opensource.alibaba.com/docs/2.x/quickstart/write 一、实现方式 1、根据需要导出的列…...

JAVA面试题11
什么是Java的访问修饰符,并列出它们的作用。 Java的访问修饰符包括public、private、protected和默认。它们的作用如下: public: 可以被任何其他类访问。 private: 只能被所在类访问,其他类无法访问。 protected: 可以被所在类和同一个包中的…...
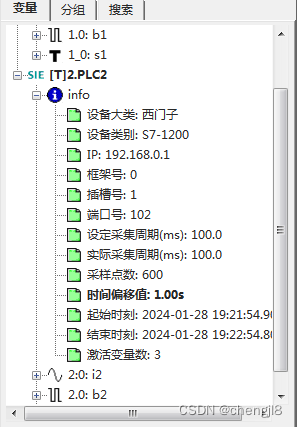
工业数据采集的时间不确定性及PLC-Recorder的通道偏移功能
目录 一、缘起 二、效果展示 三、设置方法 四、小结 一、缘起 大家都知道采集软件首先要尽可能还原数据原来的状态,给用户提供一个可以信赖的参考。但是,数据采集又有很多随机因素:Windows是一个周期不严格的系统、以太网通讯有时间波动、…...
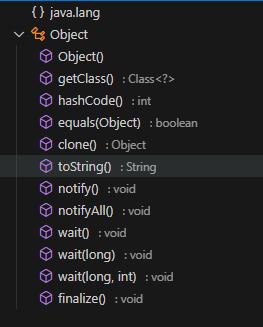
十五、Object 类
文章目录 Object 类6.1 public Object()6.2 toString方法6.3 hashCode和equals(Object)6.4 getClass方法6.5 clone方法6.6 finalize方法 Object 类 本文为书籍《Java编程的逻辑》1和《剑指Java:核心原理与应用实践》2阅读笔记 java.lang.Object类是类层次结构的根…...
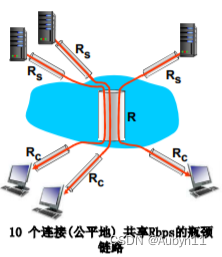
计算机网络——06分组延时、丢失和吞吐量
分组延时、丢失和吞吐量 分组丢失和延时是怎样发生的 在路由器缓冲区的分组队列 分组到达链路的速率超过了链路输出的能力分组等待排到队头、被传输 延时原因: 当当前链路有别的分组进行传输,分组没有到达队首,就会进行排队,从…...
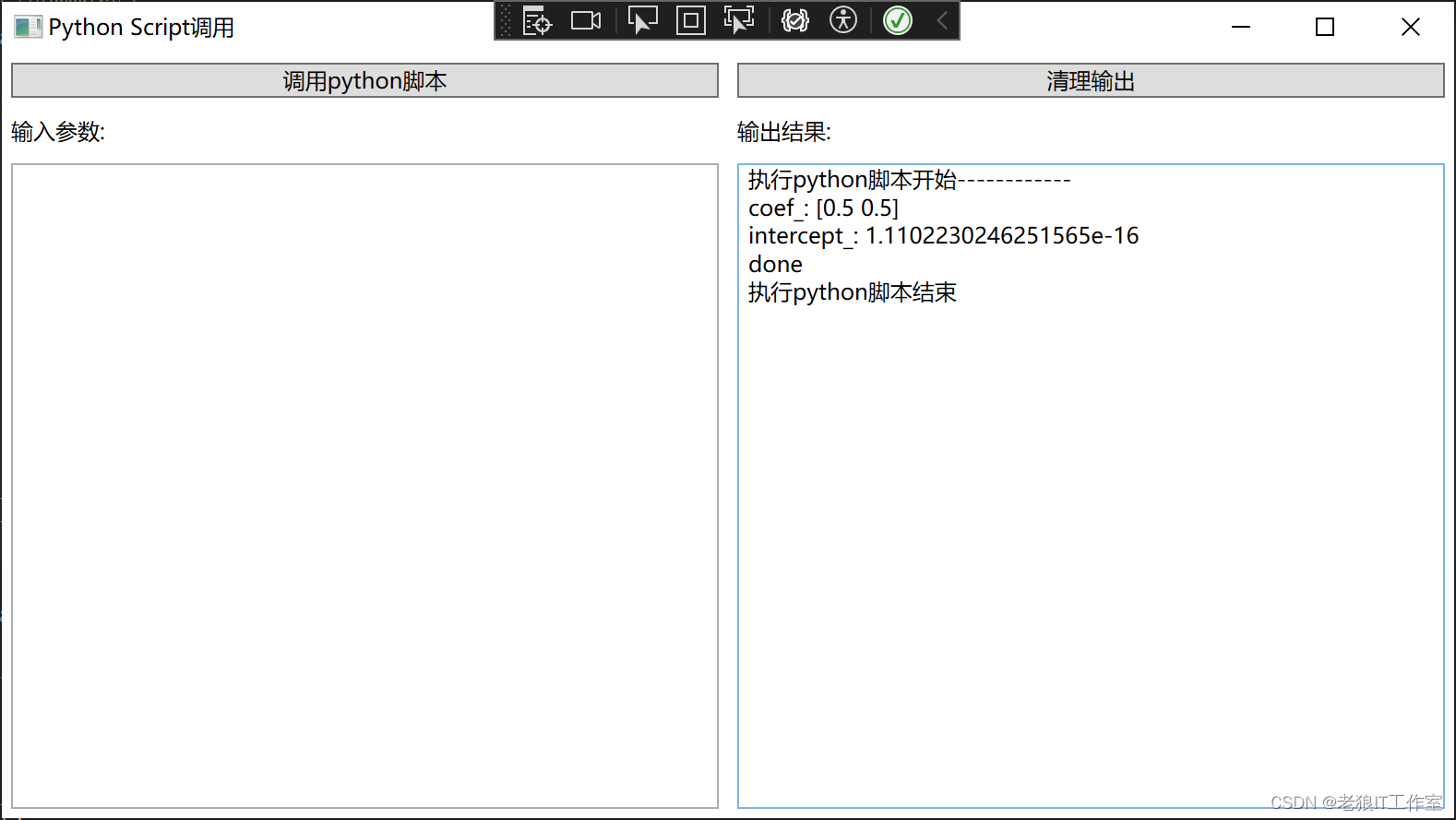
[C#] 如何调用Python脚本程序
为什么需要C#调用python? 有以下几个原因需要C#调用Python: Python拥有丰富的生态系统:Python有很多强大的第三方库和工具,可以用于数据科学、机器学习、自然语言处理等领域。通过C#调用Python,可以利用Python的生态系…...

AlmaLinux更换鼠标样式为Windows样式
文章目录 前言先看看条件与依赖第一步:测试最终效果第二步:使用CursorXP修改鼠标样式CurosrXP安装CursorXP使用 第三步:Linux端环境搭建与命令执行UbuntuFedora其他系统均失败 第四步:应用主题 前言 只不过是突发奇想,…...
BUGKU-WEB 留言板
题目描述 题目无需登录后台!需要xss平台接收flag, http协议需要http协议的xss平台打开场景后界面如下: 解题思路 看到此类的题目,应该和存储型xss有关,也就是将恶意代码保存到服务器端即然在服务器端,那就…...
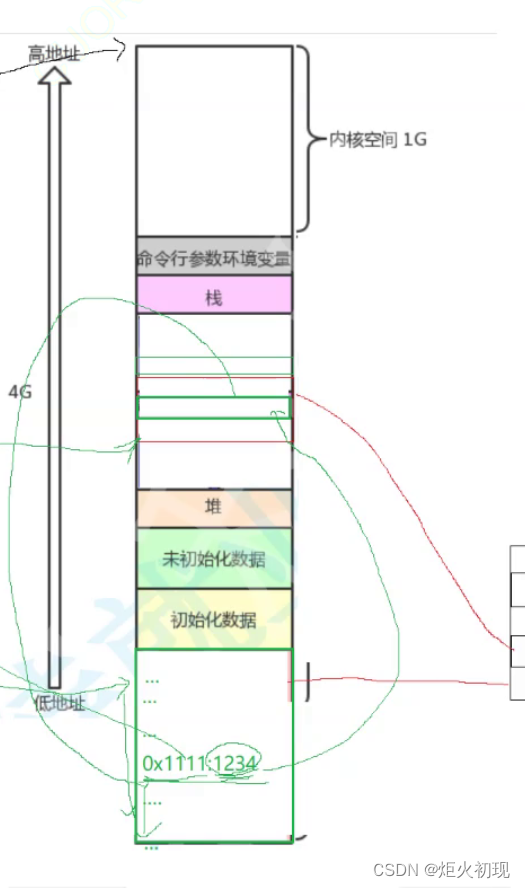
Linux之动静态库
今天我们来讲动静态库! 首先我们来粗粒度的划分一下动态库和静态库。 动态库就是只有一份库文件,所有想用该库的文件与改库文件建立链接,然后使用。这样可以提高代码复用率,避免重复拷贝产生没必要的内存消耗。 静态库…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...
