CF1845 D. Rating System [思维题+数形结合]
传送门:CF
[前题提要]:自己在做这道题的时候思路完全想错方向,导致怎么做都做不出来,看了题解之后感觉数形结合的思考方式挺好的(或者这种做法挺典的),故写篇题解记录一下
题目很简单,不再解释.先不考虑 k k k,想想是一种什么情况?很显然应该是跟下图一样是一个折线图的变化.
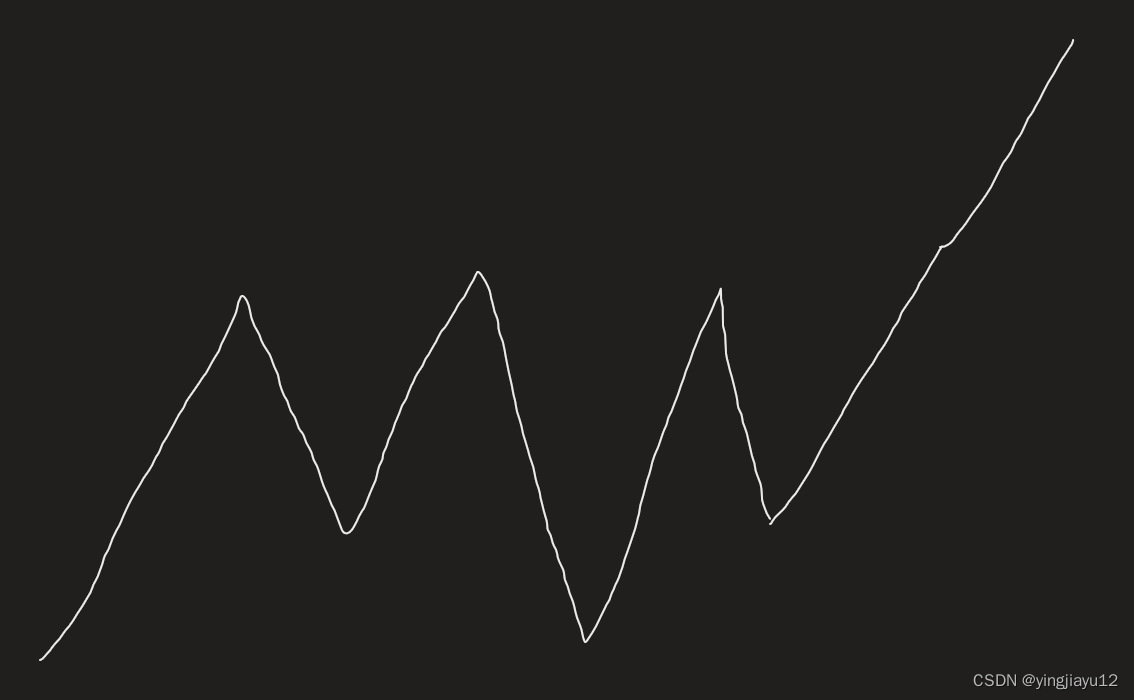
然后是一个很简单的事实:我们选取的K一定是前缀和的某一个值,更为准确的来说,应该是一个即将减少的一个前缀和值.这个结论自己把玩一下应该是不难发现的,简单的讲一下为什么是这样.因为对于一个即将减少的值来说,我们不妨选取这个值,因为这个值肯定比即将减少的那个值大,那为啥不选这个更大的值呢.而对于中间段的数来说,那些数只是中间值,两端点必然有一个点比它更为优秀.
那么现在随便选取一个端点作为我们的K,看看原图会发生什么情况
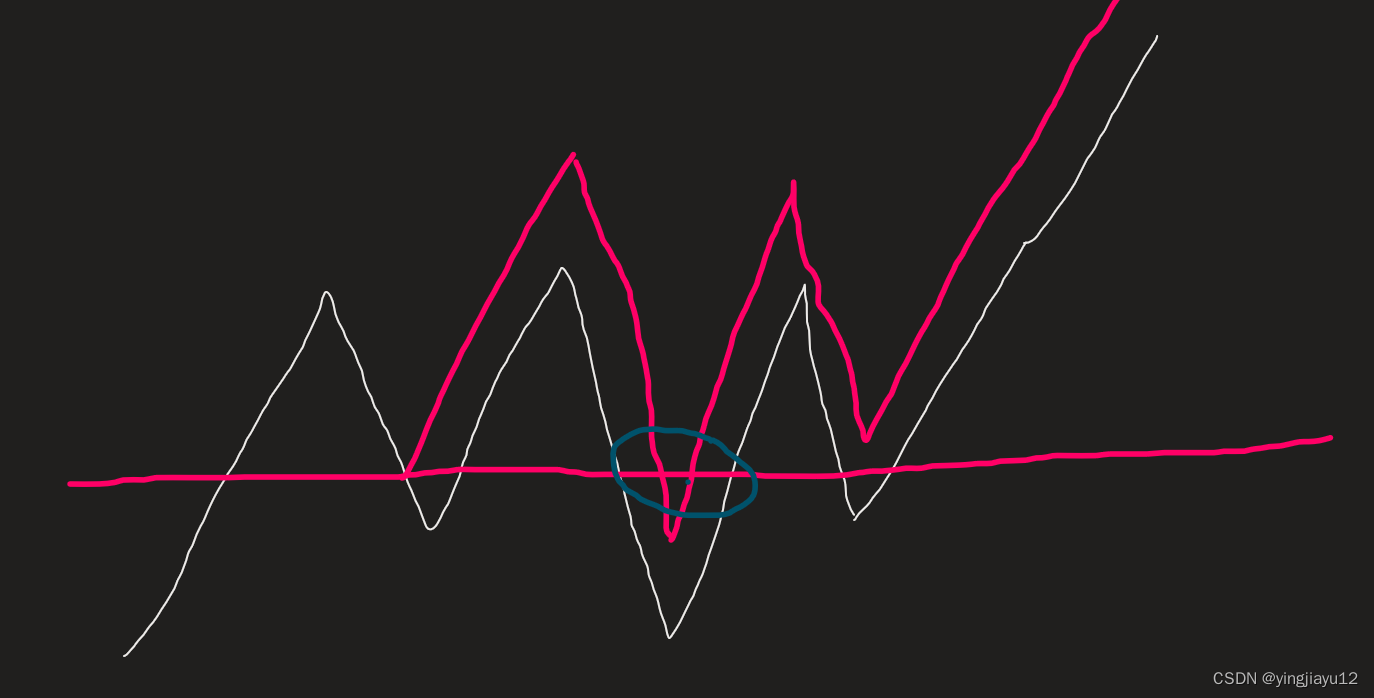
考虑选择的K的值为红横线.不难发现原本白色的折线因为现在K的出现需要往左上进行一个平移.
继续看蓝色的圈,我们会发现原本的平移还不够,我们需要将整个部分进行再一次平移.(因为懒所以没有进一步画出).
上面这段操作很重要,是这一道题的关键.仔细品一下上面的操作,我们就会发现后面那部分的贡献其实就是后缀最大后缀和(两个前缀和差其实就是后缀和啦),也就是当前位置开始的所有的后缀和的最大值.直接讲可能有点抽象,建议仔细看看上面的图的平移操作.数形结合一下很好理解.
PS:出现蓝圈的原因就是因为该后缀和更大.
那么这道题的解法也就呼之欲出了.考虑枚举每一个前缀和作为我们的K,然后计算一下贡献即可.
但是还存在一种特殊情况需要再仔细考虑一下:
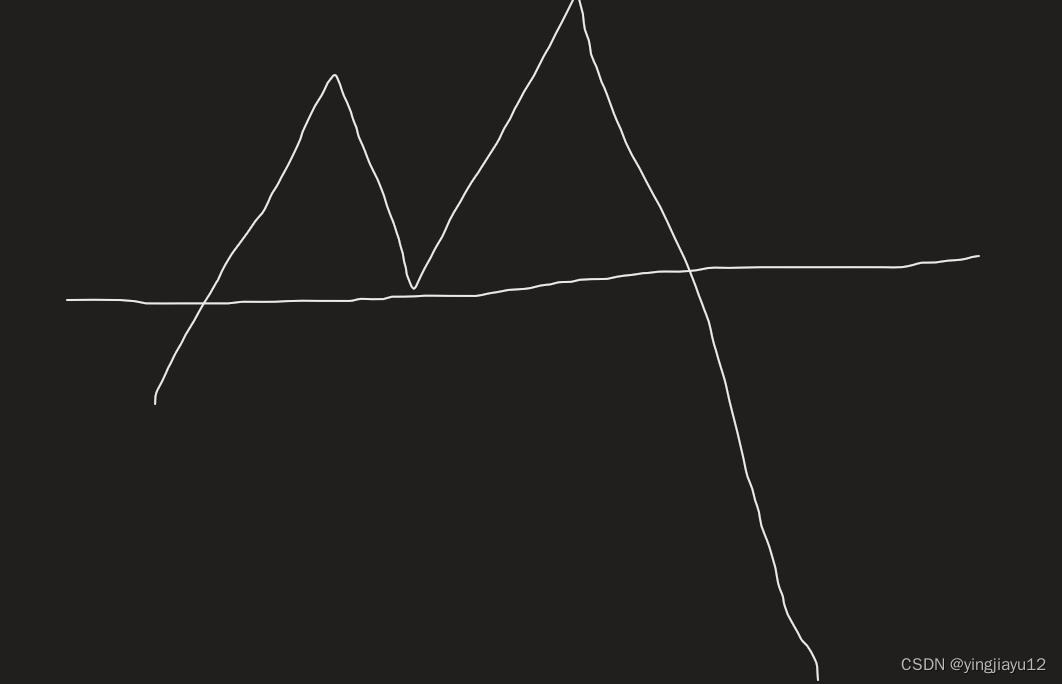
对于上图的情况,我们会发现最后一段的后缀和贡献是负的,并且此时没办法进行平移.怎么解决?想一下平移的实际意义,不难发现应该令该贡献为0,也就是后缀最大值的初始值应该定义0
下面是具体的代码部分:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls (rt<<1)
#define rs (rt<<1|1)
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
inline void print(__int128 x){if(x<0) {putchar('-');x=-x;}if(x>9) print(x/10);putchar(x%10+'0');
}
#define maxn 1000000
#define int long long
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
int a[maxn];int rmax[maxn],sum[maxn];
signed main() {int T=read();while(T--) {int n=read();for(int i=1;i<=n;i++) {a[i]=read();}for(int i=1;i<=n;i++) {sum[i]=sum[i-1]+a[i];}rmax[n]=0;for(int i=n-1;i>=0;i--) {rmax[i]=max(rmax[i+1],sum[n]-sum[i]);}int maxx=sum[n],ans=sum[n];for(int i=0;i<n;i++) {if(sum[i]+rmax[i]>maxx) {maxx=sum[i]+rmax[i];ans=sum[i];} }cout<<ans<<endl;}return 0;
}
相关文章:

CF1845 D. Rating System [思维题+数形结合]
传送门:CF [前题提要]:自己在做这道题的时候思路完全想错方向,导致怎么做都做不出来,看了题解之后感觉数形结合的思考方式挺好的(或者这种做法挺典的),故写篇题解记录一下 题目很简单,不再解释.先不考虑 k k k,想想是一种什么情况?很显然应该是跟下图一样是一个折线图的变化.…...
HeidiSQL安装配置(基于小皮面板(phpstudy))连接MySQL
下载资源 对于这款图形化工具,博主建议通过小皮面板(phpstudy)来下载即可,也是防止你下载到钓鱼软件,小皮面板(phpstudy)如果你不懂是什么,请看下面链接这篇博客 第二篇:…...

【蓝桥2013】错误票据
错误票据 题目描述 某涉密单位下发了某种票据,并要在年终全部收回。 每张票据有唯一的 ID 号。全年所有票据的 ID 号是连续的,但 ID 的开始数码是随机选定的。 因为工作人员疏忽,在录入 ID 号的时候发生了一处错误,造成了某个…...

nvm对node版本进行管理及疑难解决,vue项目搭建与启动
一、nvm安装与node版本管理 nvm安装 1、nvm地址:https://github.com/coreybutler/nvm-windows/releases 2、无需配置安装包,nvm-setup-v1.1.10.zip 解压后双击nvm-setup.exe,选择安装路径,一路next即可 打开dos窗口输入nvm vers…...
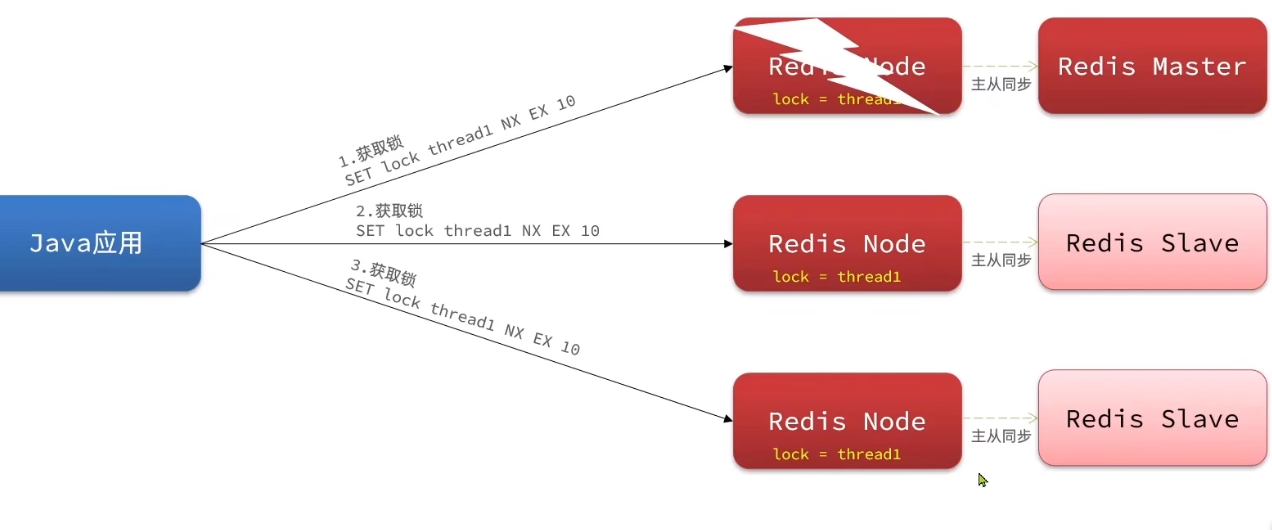
Redisson分布式锁 原理 + 运用 记录
Redisson 分布式锁 简单入门 pom <dependency><groupId>org.redisson</groupId><artifactId>redisson</artifactId><version>3.13.6</version></dependency>配置类 package com.hmdp.config;import org.redisson.Redisson;…...
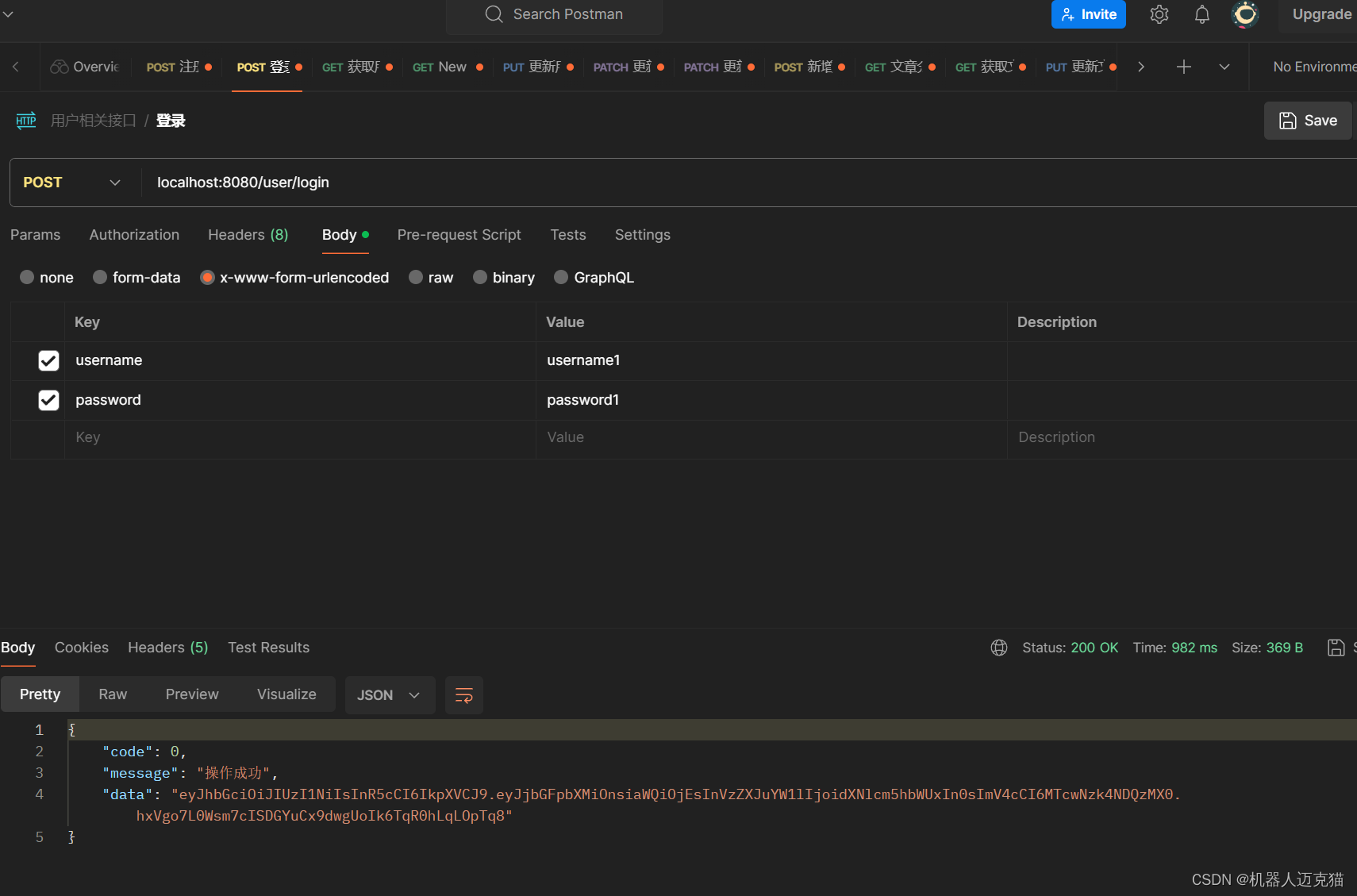
Spring Boot 笔记 021 项目部署
1.1 引入坐标,并双击package打包成jar包 1.2 在服务器上运行jar包 1.3 使用postman测试 2.1 运行配置 2.1.1 命令更改端口 java -jar big-event-1.0-SNAPSHOT.jar --server.port7777 2.1.2 环境变量更新(略) 2.1.3 外部配置文件,…...

新技术革命开始了,Sora一出,所有的视频人、电影人都下岗
Sora一出,所有的视频人、电影人都下岗! Sora直接用文本制作长达60秒的视频长镜头,也就是说,将来,只需要输入分镜脚本,电影就可以制作出来,不再需要几十人几百人声势浩大地去“拍”了,…...

【FPGA开发】Modelsim和Vivado的使用
本篇文章包含的内容 一、FPGA工程文件结构二、Modelsim的使用三、Vivado的使用3.1 建立工程3.2 分析 RTL ANALYSIS3.2.1 .xdc约束(Constraints)文件的产生 3.3 综合 SYNTHESIS3.4 执行 IMPLEMENTATION3.5 烧录程序3.6 程序固化3.6.1 SPI约束3.6.2 .bin文…...

现代浏览器对 es模块 【esm】原生支持
现代浏览器对 ES(ECMAScript)模块的原生支持是指浏览器可以直接解析和执行 JavaScript 文件中的 ES 模块语法,无需额外的工具或转换。 具体来说,当浏览器遇到 import 和 export 关键字时,会将其识别为 ES 模块语法&…...
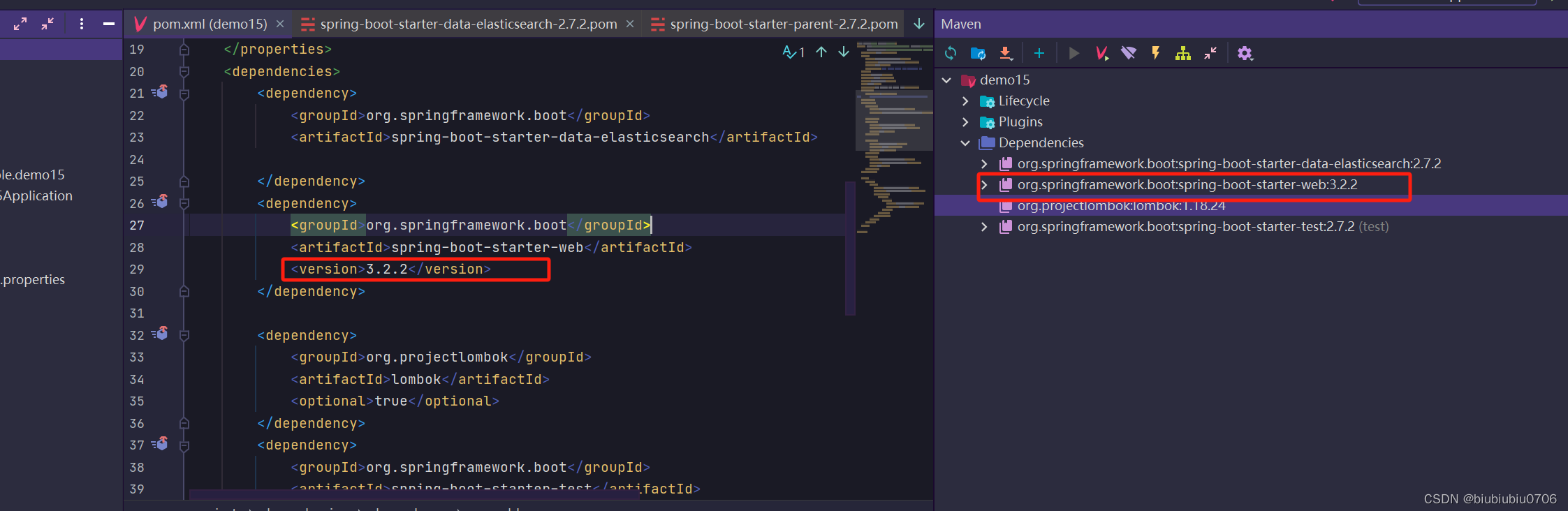
修改SpringBoot中默认依赖版本
例如SpringBoot2.7.2中ElasticSearch版本是7.17.4 我希望把它变成7.6.1...
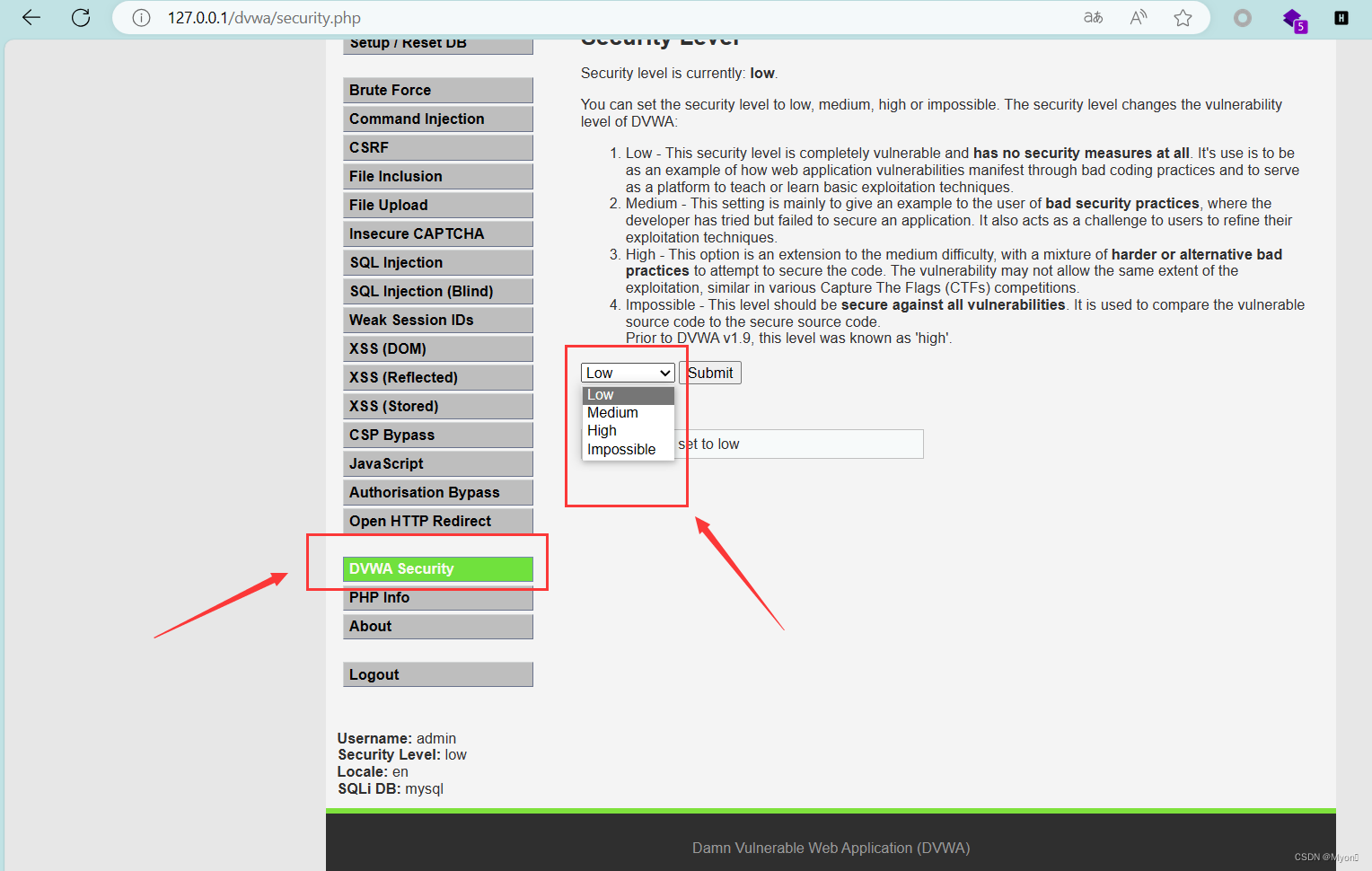
网络安全最典型基础靶场-DVWA-本地搭建与初始化
写在前面: 之前也打过这个 DVWA 靶场,但是是在虚拟机环境下的一个小块分区靶场; 本篇博客主要介绍在本地搭建 DVWA 靶场以及靶场的初始化,后续会陆续更新通关教程。 由于我们是在本地搭建,则需要基于你已经装好 phpstu…...

算法-----高精度2(高精度乘法,高精度除法,高精度斐波那锲数列)
高精度乘法 对于高精度乘法来说似乎不像高精度加减法那样简单了,我们似乎得一个一个加了,因为我们都知道 abaaaaa…a(b个a)。如果真要这要的话那1e9*1e9不得超时啊,所以不能这样,我们还是得从乘法竖式入手 这样看似乎看不出来什…...
windows vs 自己编译源码 leveldb 然后使用自己编译的文件
1 准备源码文件 1.1 第一种方法 git下载源码 vs项目中git leveldb源码和git third_party googletest-CSDN博客 1.2 第二种方法 手动下载 然后把第三方的源码下载 复制到 third_party 对应的文件夹中 没有文件夹 third_party -> powershell mkdir third_party 2 编译lev…...
基于GPT一键完成数据分析全流程的AI Agent: Streamline Analyst
大型语言模型(LLM)的兴起不仅为获取知识和解决问题开辟了新的可能性,而且催生了一些新型智能系统,例如旨在辅助用户完成特定任务的AI Copilot以及旨在自动化和自主执行复杂任务的AI Agent,使得编程、创作等任务变得高效…...

C语言-----习题
1.通过这个例题,我们可以知道*p.a是无法打印99的,因为.的优先级比解引用*高; struct S {int a;int b; }; int main() {struct S a, * p &a;//可以分为两部分理解//struct S a;//struct S *p &a;a.a 99;printf("%d\n"…...
)
Java学习笔记(五)
目录 一、控制结构 1.1 顺序控制 1.2 分支控制 (一)单分支 (二)双分支 (三)多分支 (四)嵌套分支 (五)switch分支 1.3 循环控制 (一&…...

4.【Linux】进程控制(进程终止||进程等待||程序替换)
一.进程创建fork 见上篇文章 二.进程的终止 1.进程退出场景 1.代码运行完毕,结果正确,通过main函数退出码返回一般为0。 2.代码运行完毕,结果不正确,通过不同的退出码标识不同的错误原因。 3.代码异常终止(信号&am…...

微服务设计:Spring Cloud 链路追踪概述
Spring Cloud 链路追踪是指在分布式系统中追踪请求路径的技术。它可以帮助开发者了解请求在各个微服务之间是如何流转的,以及每个微服务处理请求所花费的时间。链路追踪可以用于解决以下问题: 性能分析: 识别性能瓶颈,优化微服务性能。故障排…...
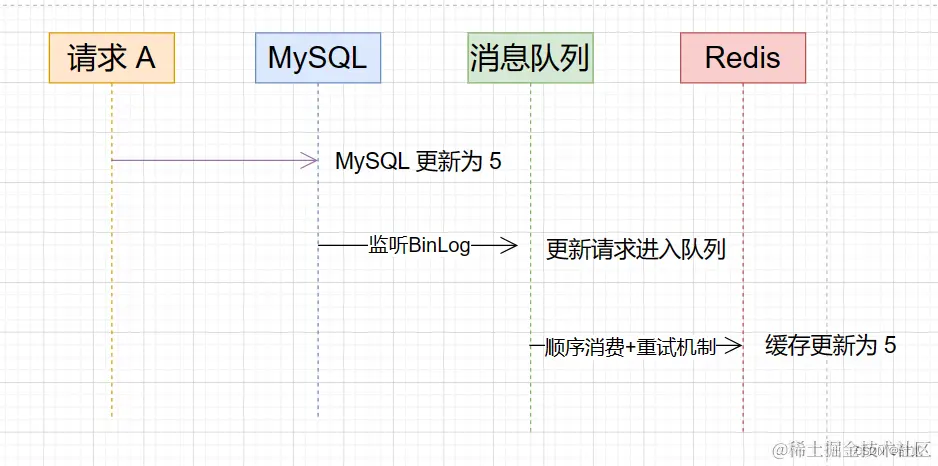
【MySQL/Redis】如何实现缓存一致
目录 不实用的方案 1. 先写 MySQL , 再写 Redis 2. 先写 Redis , 再写MySQL 3. 先删 Redis,再写 MySQL 实用的方案 1. 先删 Redis,再写 MySQL, 再删 Redis 2. 先写 MySQL , 再删 Redis 3. 先写MySQL,通过BinLog࿰…...

Socket.D 开源输传协议 v2.4.0 发布
Socket.D 协议 是基于"事件"和"语义消息""流"的网络应用层传输协议。有用户说,“Socket.D 之于 Socket,尤如 Vue 之于 Js、Mvc 之于 Http”。支持 tcp, udp, ws, kcp 传输。协议特点可参考《官网介绍》。 pyton 已开发完…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...
