算法-----高精度2(高精度乘法,高精度除法,高精度斐波那锲数列)
高精度乘法
对于高精度乘法来说似乎不像高精度加减法那样简单了,我们似乎得一个一个加了,因为我们都知道
a×b=a+a+a+a+a…+a(b个a)。如果真要这要的话那1e9*1e9不得超时啊,所以不能这样,我们还是得从乘法竖式入手

这样看似乎看不出来什么,那我们可以对其改变下模式可以进行撤位看看

这样就撤位成功了,但肯定不是 最后结果,每一位都要化成一位数。但是我们可以先等等,观察一下规律。不难发现当逆序存储后,我们做乘法竖式模拟时,c[i+j]+=a[i]*b[j](下标从零开始)。

最后我们只需进下位就行了。
所以我们的思路来了:
1.枚举a枚举b,相乘再加到c里
2.加完之后再进位
3,别忘去掉前导零
好的开始代码环节
初始化(不多说)
string s1,s2;
const int N=2050;
int a[N],b[N],c[N],len1,len2,len3;
读入
void Read(){cin>>s1>>s2;len1=s1.size(),len2=s2.size();len3=len1+len2; //c数组的长度,因为公式是c[i+j]+=a[i]*b[j],所以i+j的最大值就是c的长度for(int i=0;i<len1;i++) a[i]=(s1[len1-i-1]-'0');for(int j=0;j<len2;j++) b[j]=(s2[len2-j-1]-'0');
}
模拟竖式
void count(){for(int i=0;i<len1;i++){//枚举afor(int j=0;j<len2;j++){//枚举bc[i+j]+=a[i]*b[j];//公式}} for(int i=0;i<len3;i++){//进位if(c[i]>=10){c[i+1]+=c[i]/10;c[i]%=10;}}while(len3>0&&c[len3-1]==0) len3--; //去前导零
}
输出
void print(){for(int i=len3-1;i>=0;i--) cout<<c[i];
}
总代码
#include<bits/stdc++.h>
using namespace std;
string s1,s2;
const int N=2050;
int a[N],b[N],c[N],len1,len2,len3;
void Read(){cin>>s1>>s2;len1=s1.size(),len2=s2.size();len3=len1+len2;for(int i=0;i<len1;i++) a[i]=(s1[len1-i-1]-'0');for(int j=0;j<len2;j++) b[j]=(s2[len2-j-1]-'0');
}
void count(){for(int i=0;i<len1;i++){for(int j=0;j<len2;j++){c[i+j]+=a[i]*b[j];}} for(int i=0;i<len3;i++){if(c[i]>=10){c[i+1]+=c[i]/10;c[i]%=10;}}while(len3>0&&c[len3-1]==0) len3--;
}
void print(){for(int i=len3-1;i>=0;i--) cout<<c[i];
}
int main()
{
Read();
count();
print();return 0;
}
高精度除法
高精度除以低精度
因为除数是低精度,所以我们不用竖式就能解,用逐位相除法。

初始化+读入(因为是除法所以不用逆序存储,正着就行)
string s;
const int N=1050;
int a[N],c[N],b,len,lenc=1,x;
void Read(){cin>>s>>b;len=s.size();for(int i=1;i<=len;i++) a[i]=s[i-1]-'0';//顺着存
}
运算
因为除法如果不够除的话是填零(或是有余),我们可以将不够除(或除完的余数)的放入后面让他和后面的数一起除,不过要注意*10因为他们的单位不同,当然有时候我们会求余数,所以我们可以带入余数让计算的更简单些。
void count(){for(int i=1;i<=len;i++){c[i]=(x*10+a[i])/b;//带着余数除当除到最后一位时%后就是余数x=(x*10+a[i])%b;}while(lenc<len&&c[lenc]==0) lenc++;
}
输出
void print(){while(lenc<=len) cout<<c[lenc++];cout<<"\n";cout<<x;
}
总代码
#include<bits/stdc++.h>
using namespace std;
string s;
const int N=1050;
int a[N],c[N],b,len,lenc=1,x;
void Read(){cin>>s>>b;len=s.size();for(int i=1;i<=len;i++) a[i]=s[i-1]-'0';
}
void count(){for(int i=1;i<=len;i++){c[i]=(x*10+a[i])/b;x=(x*10+a[i])%b;}while(lenc<len&&c[lenc]==0) lenc++;
}
void print(){while(lenc<=len) cout<<c[lenc++];cout<<"\n";cout<<x;
}
int main()
{
Read();
count();
print();return 0;
}
高精度除以高精度
高精度除以高精度,第一眼肯定是竖式,但你用竖式算过后会发现,似乎难找到怎么做。所以我们得从其他方面入手,先看看除法算式a/b,平平无奇,写下结果后呢?a/b=c…d,看到这个算式大家应该有点印象了,二三年级时我们学习的除法各个元素之间的关系:
1.a=b×c+d
2.b=(a-d)/c
3.c=(a-d)/b
4.d=a-b×c
随后我们再回顾下除法的定义:把一个数平均分成几份。根据这几条不难发现,a/b,不就是a-c个b吗
所以我们便能开始写代码了
初始化+读入(注意这里出现减法了得倒序)
#define N 1050
int a[N],b[N],c[N],d,i;
void init(int a[]){string s;cin>>s;a[0]=s.size();for(int i=1;i<=a[0];i++) a[i]=s[a[0]-i]-'0';
}
判断大小函数(因为是减法替除法,要判断下,如果a<b就要终止)
int compare(int a[],int b[]){ int i;if(a[0]>b[0]) return 1;if(a[0]<b[0]) return -1;for(i=a[0];i>0;i--){if(a[i]>b[i]) return 1;if(a[i]<b[i]) return -1;}return 0;
}
移动函数,因为单位不统一,要将单位统一才能做减法
void numcpy(int p[],int q[],int det){for(int i=1;i<=p[0];i++) q[i+det-1]=p[i];q[0]=p[0]+det-1;
}
减法函数与除法函数
void jian(int a[],int b[]){int flag,i;flag=compare(a,b);if(flag==0){a[0]=0;return;}if(flag==1){for(i=1;i<=a[0];i++){if(a[i]<b[i]){a[i+1]--;a[i]+=10;}a[i]-=b[i]; }while(a[0]>0&&a[a[0]]==0) a[0]--;return; }
}
void chugao(int a[],int b[],int c[]){int i,tmp[N];c[0]=a[0]-b[0]+1;for(i=c[0];i>0;i--){memset(tmp,0,sizeof tmp);numcpy(b,tmp,i);while(compare(a,tmp)>=0){c[i]++;jian(a,tmp);}}while(c[0]>0&&c[c[0]]==0) c[0]--;return;
}
最后输出
void print(int a[]){int i;if(a[0]==0){cout<<0<<endl;return;}for(i=a[0];i>0;i--) cout<<a[i];cout<<endl;return;
}
总代码
#include<bits/stdc++.h>
using namespace std;
#define N 1050
int a[N],b[N],c[N],d,i;
void init(int a[]){string s;cin>>s;a[0]=s.length();for(int i=1;i<=a[0];i++) a[i]=s[a[0]-i]-'0';
}
void print(int a[]){int i;if(a[0]==0){cout<<0<<endl;return;}for(i=a[0];i>0;i--) cout<<a[i];cout<<endl;return;
}
int compare(int a[],int b[]){ int i;if(a[0]>b[0]) return 1;if(a[0]<b[0]) return -1;for(i=a[0];i>0;i--){if(a[i]>b[i]) return 1;if(a[i]<b[i]) return -1;}return 0;
}
void jian(int a[],int b[]){int flag,i;flag=compare(a,b);if(flag==0){a[0]=0;return;}if(flag==1){for(i=1;i<=a[0];i++){if(a[i]<b[i]){a[i+1]--;a[i]+=10;}a[i]-=b[i]; }while(a[0]>0&&a[a[0]]==0) a[0]--;return; }
}
void numcpy(int p[],int q[],int det){for(int i=1;i<=p[0];i++) q[i+det-1]=p[i];q[0]=p[0]+det-1;
}
void chugao(int a[],int b[],int c[]){int i,tmp[N];c[0]=a[0]-b[0]+1;for(i=c[0];i>0;i--){memset(tmp,0,sizeof tmp);numcpy(b,tmp,i);while(compare(a,tmp)>=0){c[i]++;jian(a,tmp);}}while(c[0]>0&&c[c[0]]==0) c[0]--;return;
}
int main()
{
init(a);
init(b);
chugao(a,b,c);
print(c);
print(a);//通过减法最后的a就是余数return 0;
}
高精度斐波那契数列
f[1]=1
f[2]=1
f[i]=f[i−1]+f[i−2]
求f[n]
输入
输入一个整数n
输出
输出一个整数
样例
输入 1
3
输出 1
2
提示
n<=200
【分析】这题目肯定要高精度的因为当n到100时都已经是354224848179261915075(别问我答案哪来的)了,long long 都存不下,所以的用高精度加法一步步加
好的高精度加法模板来了(没有读入)
const int N=1050;
int a[N],b[N],c[N],len=1,len1=1,len2=1;
void count(){int jw=0;for(int i=0;i<len;i++){c[i]=jw+a[i]+b[i];jw=c[i]/10;c[i]%=10;}if(jw==1){c[len]=1;len++;}while(len>1&&c[len-1]==0) len--;
}
void print(){
for(int i=len-1;i>=0;i--) cout<<c[i];
}
然后主函数部分是输出n,
对于这个n我们得先特判掉一些
if(n==1||n==2){cout<<1;return 0;
}
随后因为斐波那锲数列数f(n)=f(n-1)+f(n-2),我们的先存入前两项
a[0]=1;
b[0]=1;
然后就是动规的模板了
for(int i=3;i<=n;i++){
c=a+b;
a=b;
b=c;
}
简单带入下便是
for(int i=3;i<=n;i++)
{count();len1=len2;for(int i=0;i<len2;i++){//数组赋值a[i]=b[i];}len2=len;for(int i=0;i<len;i++) b[i]=c[i];
}
最后别忘记输出
总代码
#include<bits/stdc++.h>
using namespace std;
const int N=1050;
int a[N],b[N],c[N],len=1,len1=1,len2=1;
void count(){int jw=0;for(int i=0;i<len;i++){c[i]=jw+a[i]+b[i];jw=c[i]/10;c[i]%=10;}if(jw==1){c[len]=1;len++;}while(len>1&&c[len-1]==0) len--;
}
void print(){
for(int i=len-1;i>=0;i--) cout<<c[i];
}
int main(){
int n;
cin>>n;
if(n==1||n==2){cout<<1;return 0;
}
a[0]=1;
b[0]=1;
for(int i=3;i<=n;i++)
{count();len1=len2;for(int i=0;i<len2;i++){a[i]=b[i];}len2=len;for(int i=0;i<len;i++) b[i]=c[i];
}
print();
return 0;
}
完结!
相关文章:

算法-----高精度2(高精度乘法,高精度除法,高精度斐波那锲数列)
高精度乘法 对于高精度乘法来说似乎不像高精度加减法那样简单了,我们似乎得一个一个加了,因为我们都知道 abaaaaa…a(b个a)。如果真要这要的话那1e9*1e9不得超时啊,所以不能这样,我们还是得从乘法竖式入手 这样看似乎看不出来什…...
windows vs 自己编译源码 leveldb 然后使用自己编译的文件
1 准备源码文件 1.1 第一种方法 git下载源码 vs项目中git leveldb源码和git third_party googletest-CSDN博客 1.2 第二种方法 手动下载 然后把第三方的源码下载 复制到 third_party 对应的文件夹中 没有文件夹 third_party -> powershell mkdir third_party 2 编译lev…...
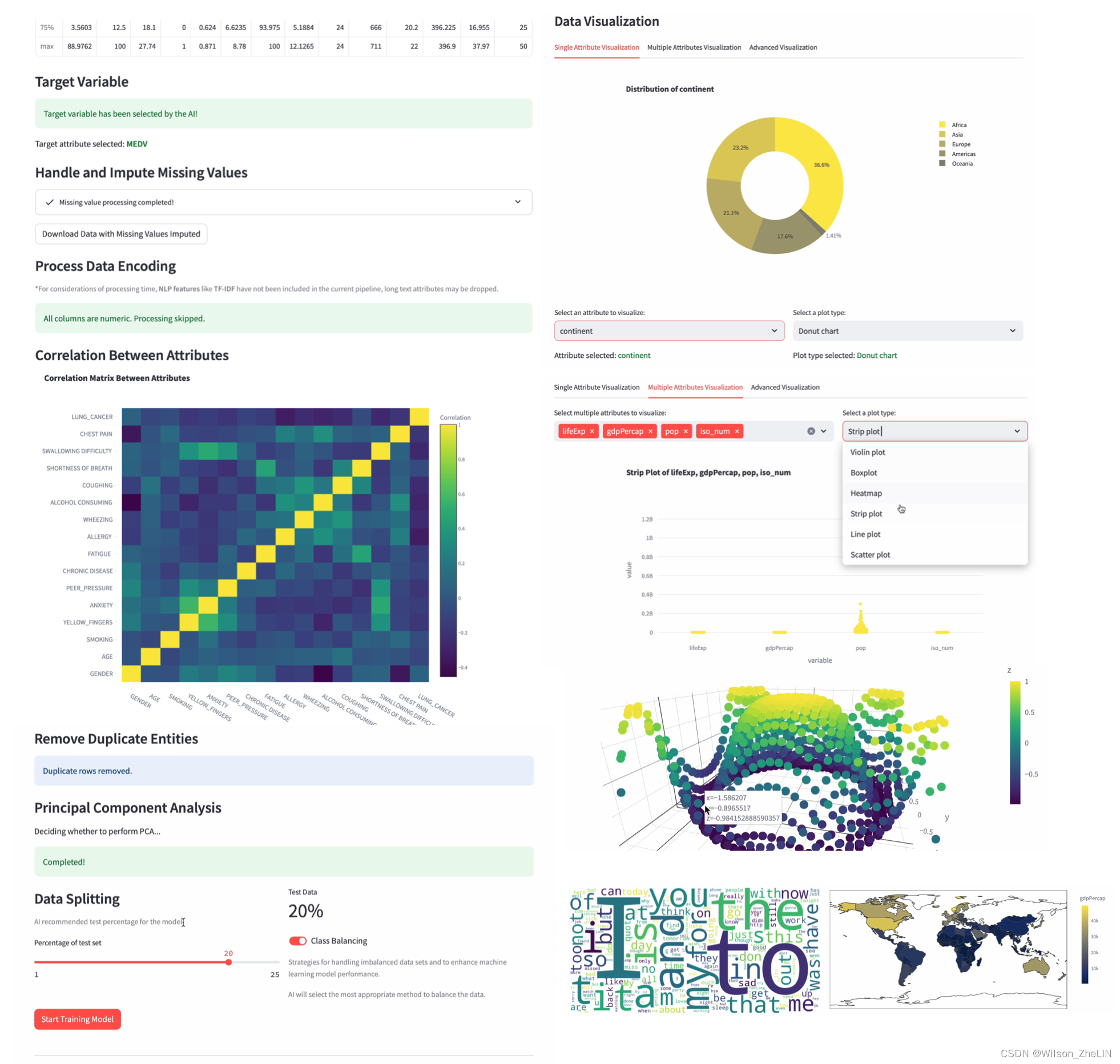
基于GPT一键完成数据分析全流程的AI Agent: Streamline Analyst
大型语言模型(LLM)的兴起不仅为获取知识和解决问题开辟了新的可能性,而且催生了一些新型智能系统,例如旨在辅助用户完成特定任务的AI Copilot以及旨在自动化和自主执行复杂任务的AI Agent,使得编程、创作等任务变得高效…...

C语言-----习题
1.通过这个例题,我们可以知道*p.a是无法打印99的,因为.的优先级比解引用*高; struct S {int a;int b; }; int main() {struct S a, * p &a;//可以分为两部分理解//struct S a;//struct S *p &a;a.a 99;printf("%d\n"…...
)
Java学习笔记(五)
目录 一、控制结构 1.1 顺序控制 1.2 分支控制 (一)单分支 (二)双分支 (三)多分支 (四)嵌套分支 (五)switch分支 1.3 循环控制 (一&…...

4.【Linux】进程控制(进程终止||进程等待||程序替换)
一.进程创建fork 见上篇文章 二.进程的终止 1.进程退出场景 1.代码运行完毕,结果正确,通过main函数退出码返回一般为0。 2.代码运行完毕,结果不正确,通过不同的退出码标识不同的错误原因。 3.代码异常终止(信号&am…...

微服务设计:Spring Cloud 链路追踪概述
Spring Cloud 链路追踪是指在分布式系统中追踪请求路径的技术。它可以帮助开发者了解请求在各个微服务之间是如何流转的,以及每个微服务处理请求所花费的时间。链路追踪可以用于解决以下问题: 性能分析: 识别性能瓶颈,优化微服务性能。故障排…...
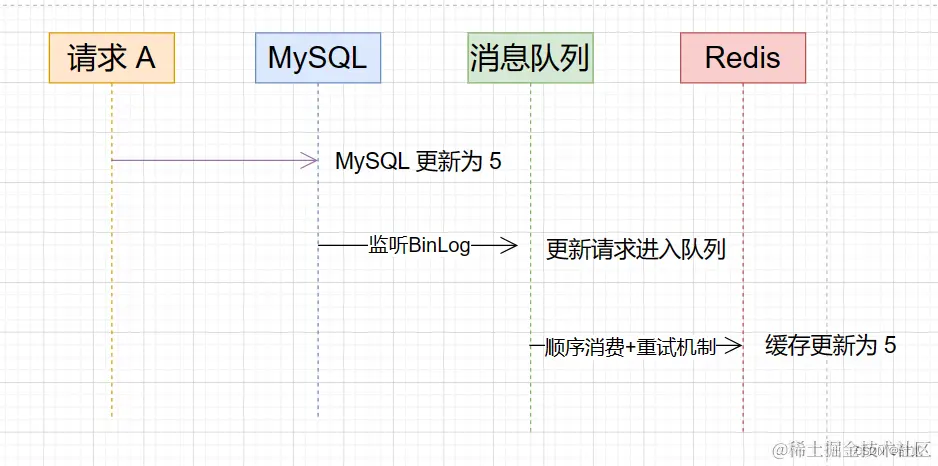
【MySQL/Redis】如何实现缓存一致
目录 不实用的方案 1. 先写 MySQL , 再写 Redis 2. 先写 Redis , 再写MySQL 3. 先删 Redis,再写 MySQL 实用的方案 1. 先删 Redis,再写 MySQL, 再删 Redis 2. 先写 MySQL , 再删 Redis 3. 先写MySQL,通过BinLog࿰…...

Socket.D 开源输传协议 v2.4.0 发布
Socket.D 协议 是基于"事件"和"语义消息""流"的网络应用层传输协议。有用户说,“Socket.D 之于 Socket,尤如 Vue 之于 Js、Mvc 之于 Http”。支持 tcp, udp, ws, kcp 传输。协议特点可参考《官网介绍》。 pyton 已开发完…...

单片机学习笔记---AT24C02数据存储
目录 AT24C02数据存储 准备工作 代码讲解 I2C.c 模拟起始位置的时序 模拟发送一个字节的时序 模拟接收应答的时序 模拟接收一个字节的时序 模拟发送应答的时序 模拟结束位置的时序 I2C.h AT24C02.c 字节写:在WORD ADDRESS(字地址ÿ…...
首次安装Mysql数据库
1、在mysql官网下载自己需要的版本 2、选择安装类型 3、 检查一下需求版本 4、 这里可能会弹出如下信息,先不用管这一步,点击Yes继续即可 5、 安装需要的环境,点击执行就可以,此过程会比较慢 如下就是全面安装完成了,点击next即可...
No.1 - No.20)
2024 前端面试题(GPT回答 + 示例代码 + 解释)No.1 - No.20
本文题目来源于全网收集,答案来源于 ChatGPT 和 博主(的小部分……) 格式:题目 h3 回答 text 参考大佬博客补充 text 示例代码 code 解释 quote 补充 quote 目录 No.1 - No.20 本文题目来源于全网收集,答案来源于…...

通过`ssh`同步`tmux`剪贴板内容
通过ssh同步tmux剪贴板内容 通过ssh连接远程服务器时,可以通过xclip同步tmux剪贴板内容。这需要在服务器上安装xclip,且需要在ssh远程连接时开启X11。 此处附tmux剪贴板调用xclip的配置: # Copy the current buffer to the system clipboa…...

HTTP 响应状态代码
HTTP 响应状态代码 HTTP 响应状态代码指示特定 HTTP 请求是否已成功完成。 响应分为五类: 信息性回复 ( 100 – 199)成功响应 ( 200 – 299)重定向消息 ( 300 – 399)客户端错误响应 ( 400 – 499)服务器错误…...

[OPEN SQL] 新增数据
INSERT语句用于数据的新增操作 本次操作使用的数据库表为SCUSTOM,其字段内容如下所示 航班用户(SCUSTOM) 该数据库表中的部分值如下所示 1.插入单条数据 语法格式 INSERT <dbtab> FROM <wa>. INSERT INTO <dbtab> VALUES <wa>. INSERT &…...
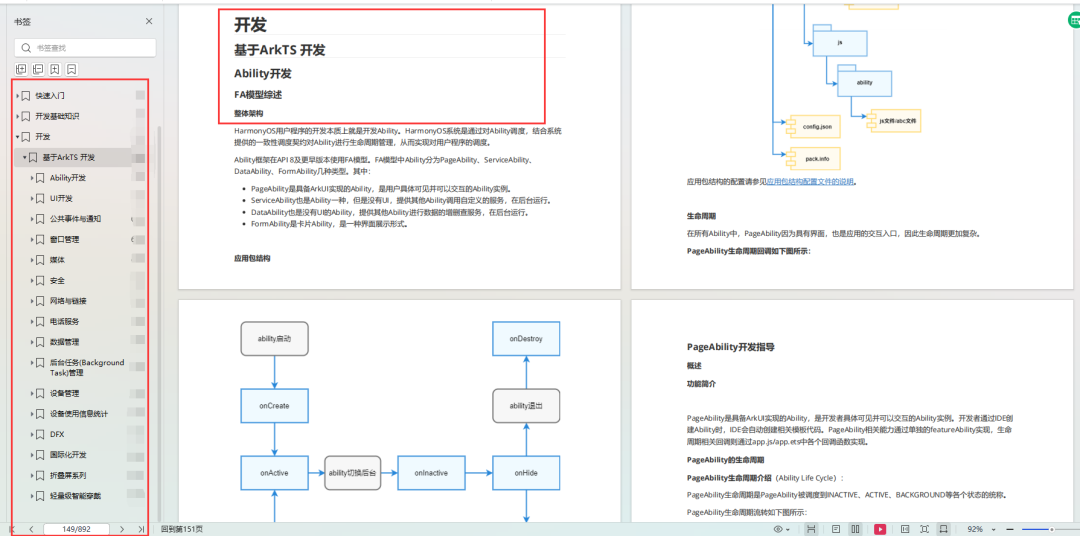
OpenHarmony—UIAbility组件生命周期
概述 当用户打开、切换和返回到对应应用时,应用中的UIAbility实例会在其生命周期的不同状态之间转换。UIAbility类提供了一系列回调,通过这些回调可以知道当前UIAbility实例的某个状态发生改变,会经过UIAbility实例的创建和销毁,…...

Mybatis的使用
MyBatis 是一个流行的 Java 持久层框架,它提供了 SQL 映射和对象关系映射的功能,让开发者能够更加便捷地操作数据库。MyBatis 通过 XML 或注解的方式配置 SQL 语句,并将 Java 对象与数据库表进行映射,以简化 JDBC 的复杂操作。以下…...

Python 播放音乐
本篇是使用Python pygame库来实现操作音乐。 安装pygame 播放音乐需要pygame库,如果没有可以进行安装。 命令如下: pip install pygame 引入类库 需要引入两个类库,即time和pygame。 示例如下: import time import pygame 播…...

[嵌入式系统-21]:RT-Thread -7- 内核组件编程接口 - 定时器
目录 一、RT-Thread定时器 1.1 概述 1.2 定时器的种类 1.2.1 周期性 1.2.2 实时性 1.2.3 功能 二、 RT-Thread 定时器的一般步骤 2.1 步骤 2.2 Flag 2.3 示例 一、RT-Thread定时器 1.1 概述 在 RT-Thread 中,定时器是一种常用的机制,用于在指…...
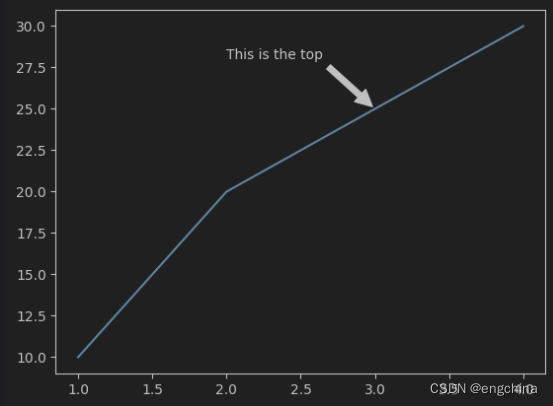
Python Matplotlib 的学习笔记
Python Matplotlib 的学习笔记 0. Python Matplotlib 简介1. 为什么要用 Matplotlib?2. Matplotlib 基础类详解2-1. Line(线)2-2. Marker(标记)2-3. Text(文本)2-4. Legend(图例&…...

从零实现富文本编辑器#5-编辑器选区模型的状态结构表达
先前我们总结了浏览器选区模型的交互策略,并且实现了基本的选区操作,还调研了自绘选区的实现。那么相对的,我们还需要设计编辑器的选区表达,也可以称为模型选区。编辑器中应用变更时的操作范围,就是以模型选区为基准来…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...
