Codeforces Round 926 (Div. 2)(A~C)
A. Sasha and the Beautiful Array

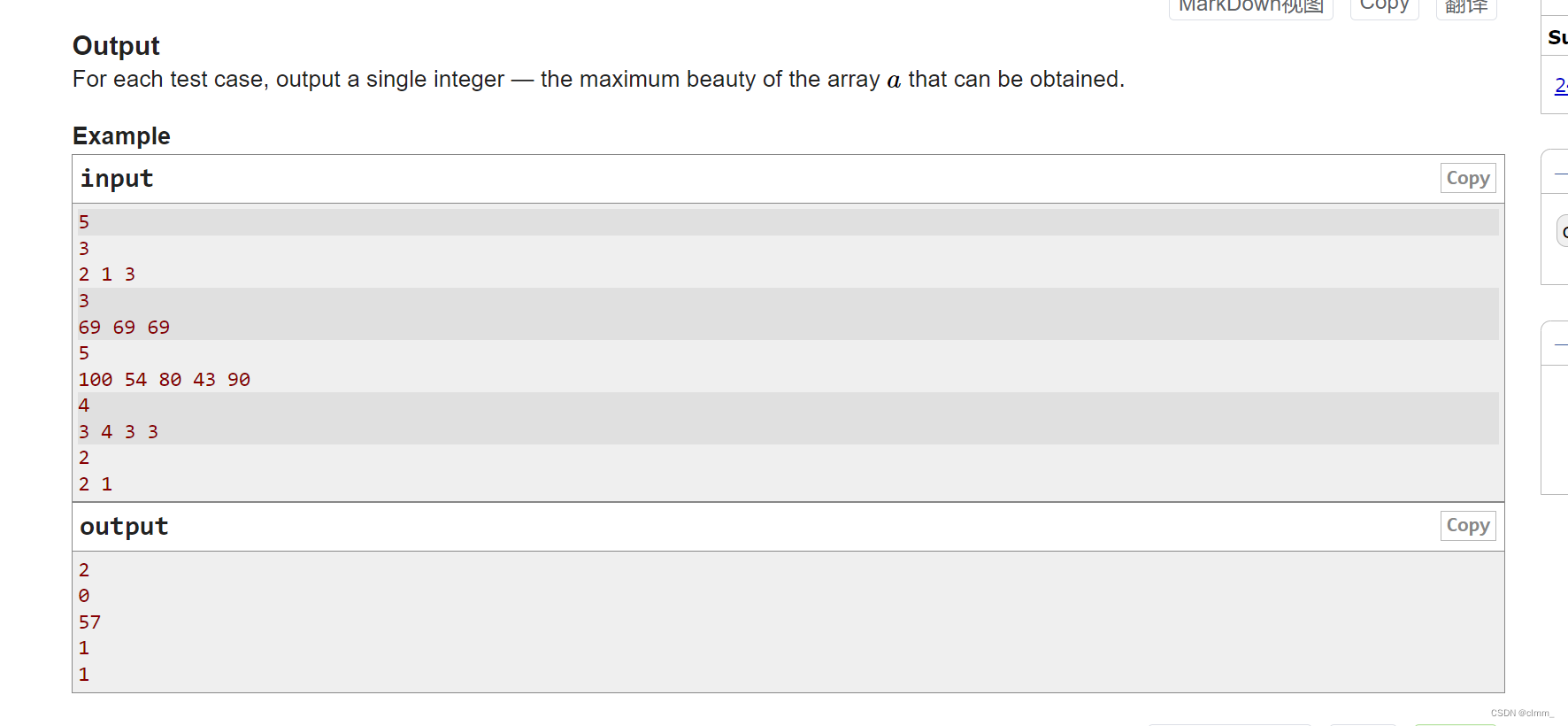
分析:说实话,打比赛的时候看到这题没多想,过了一下样例发现将数组排序一下就行,交了就过了。刚刚写题解反应过来,a2-a1+a3-a2.....an-a(n-1) = an - a1,所以最后结果只取决于最大和最小的差。
int a[N];
void solve() {int n; cin >> n;rep(i, 1, n) cin >> a[i];sort(a + 1, a + 1 + n);int ans = 0;rep(i, 2, n) {ans += a[i] - a[i - 1];}cout << ans << endl;
}B. Sasha and the Drawing


分析:同样是过了第三个样例发现,只需要涂第一排和最后一排就行了,而且(1,1)和(1,n)要放在最后涂,因为先把别的格子涂满,每涂一个格子贡献+2,最后(1,1)和(1,n)这两个格子,每格贡献+1。
void solve() {int n, k; cin >> n >> k;int cnt = 4 * n - 2 - 2;int d = k - cnt;//tans;if (d <= 0) {if (k % 2) k++;cout << k / 2 << endl;}else {cout << cnt / 2 + d << endl;}}C. Sasha and the Casino


题意:每次下注y元,输了失去y元,赢了得到y*k元(也就是增加y*(k-1)元,如果加上下注的本金就算y*k元了)。
sasha不会连续输x次,也就是说如果连输x次,第x+1次必赢。
最后问,sasha能不能依靠赌博,来无限赢钱。
反思:做题的时候陷入一个误区,我前x场都输掉,然后第x+1场把剩下的钱全下注了,那么只要本金足够,这样不是很好赢钱吗?其实不是的,因为赌场不会一直让你前x场全输的,可能会在第x-1场让你赢一下,“刷新”一下你输的场数。还有一个很需要反思的事情,明明之前一直提醒自己,做题要勤列公式,可是当时脑抽了一直在钻牛角尖没列公式。。。
分析:
我们要保证每一轮赢的钱>输的钱,这样我们才能赢到无限的钱。一轮的结尾是赢的那一把,因为我们一旦赢了,就“刷新”了我们输的场数。
上面说了,在第1~x场,赌场可能会让你赢一场,而如果1~x场全输了,第x+1场必赢。
我们可以得出一个结论:1~x+1场,我们必赢一场!这是重点
一轮中,当我们在第i场(1<=i<=x+1)赢了,说明第1 ~ i-1场是输的,因此我们在第i场赢的前要大于前i-1场输的钱。
可以得到公式
有
,yi表示第i场下注的金额
sum =
,sum表示输的金额
win = yi*(k-1),win表示在第i场赢的金额
win - sum > 0
yi > sum / (k-1)
说明,我们第i场的下注金额yi至少是 sum/(k-1)+1。
而到了第i场我们还剩下 a-sum元,
因此得到了不等式,sum/(k-1) + 1 <= a-sum
int k, x, a;void solve() {cin >> k >> x >> a;int sum = 0;int f = 1;rep(i, 1, x + 1) {int y = sum / (k - 1) + 1;if (y <= a - sum) {//有钱下注。然后我们要假设输掉这场sum += y;}else {//没钱下注,就算赢了也没用f = 0;break;}}//tans;if (!f) cout << "NO" << endl;else cout << "YES" << endl;
}相关文章:
Codeforces Round 926 (Div. 2)(A~C)
A. Sasha and the Beautiful Array 分析:说实话,打比赛的时候看到这题没多想,过了一下样例发现将数组排序一下就行,交了就过了。刚刚写题解反应过来,a2-a1a3-a2.....an-a(n-1) an - a1,所以最后结果只取决…...

Godot 游戏引擎个人评价和2024年规划(无代码)
文章目录 前言Godot C# .net core 开发简单评价Godot相关网址可行性 Godot(GDScirpt) Vs CocosGodot VS UnityUnity 的裁员Unity的股票Unity的历史遗留问题:Mono和.net core.net core的开发者,微软 个人的独立游戏Steam平台分成说明独立游戏的选题美术风…...
Win11关闭Windows Defender实时保护,暂时关闭和永久关闭方法 | Win10怎么永久关闭Windows Defender实时保护
文章目录 1. 按2. 暂时关闭Windows Defender实时保护3. 永久关闭实时保护 1. 按 开启Windows Defender实时保护有时候会导致系统变得异常卡顿,严重影响系统的流畅度,并且由于会有几率错误拦截和查杀我们的正常操作,所以还会导致我们的程序无…...

C# CAD2016 宗地生成界址点,界址点编号及排序
1 、界址点起点位置C# CAD2016 多边形顶点按方向重新排序 2、 界址点顺时针逆时针走向 C# CAD2016 判断多边形的方向正时针或逆时针旋转 3、块文件插入 //已知块文件名称 GXGLQTC //块文件需要插入的坐标点 scaledPoint// 插入块到当前图纸中的指定位置ObjectId newBlockId;B…...
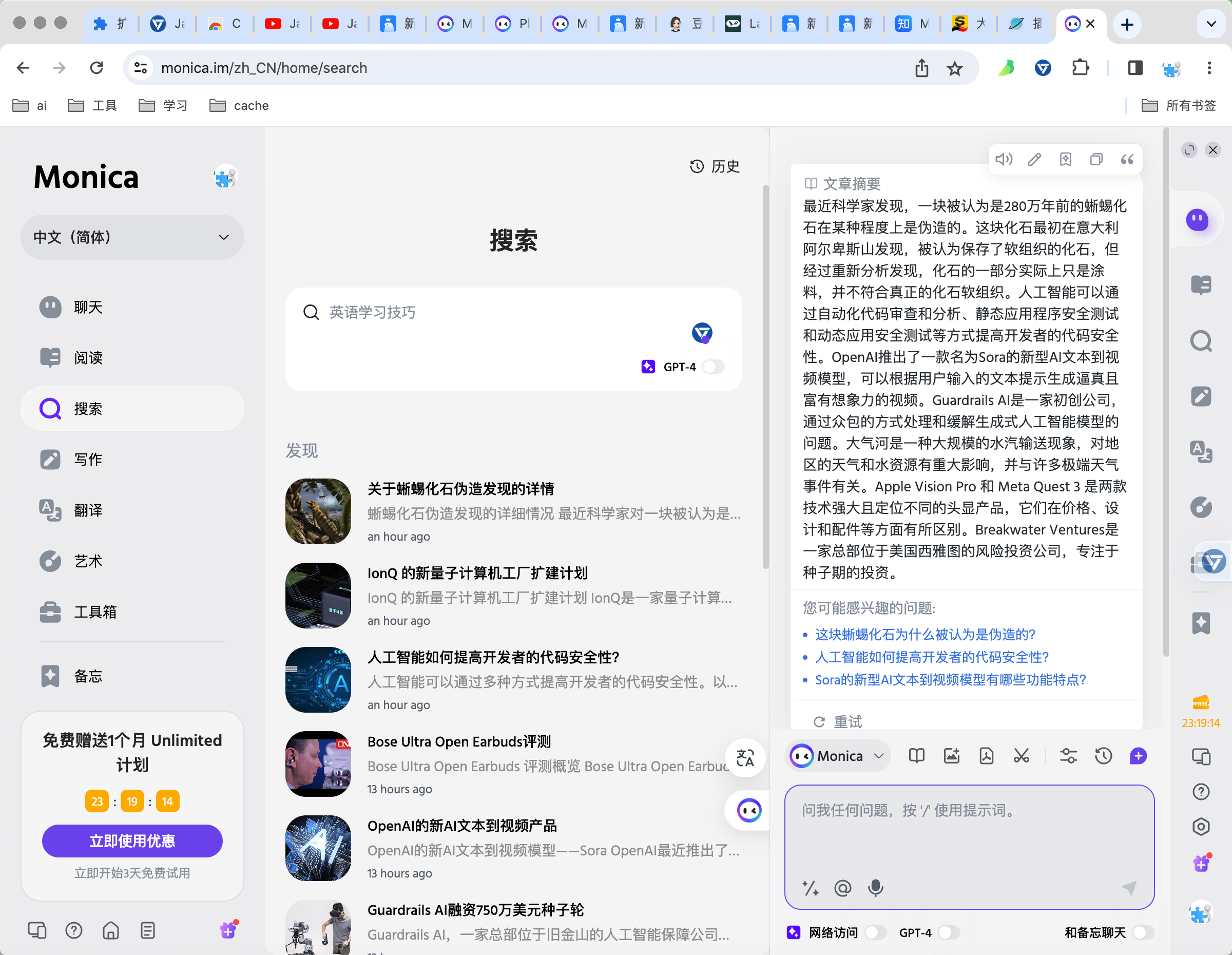
[ai笔记7] google浏览器ai学习提效定制优化+常用插件推荐
欢迎来到文思源想的ai空间,这是技术老兵重学ai以及成长思考的第7篇分享! 工欲善其事必先利其器,为了ai学习的效能提升,放假期间对google浏览器做了一次系统整改,添加了一些配置和插件,这里既有一些显示、主…...

联想thinkpad-E450双系统升级记
早期笔记本联想thinkpad-E450双系统 大约16年花4000多大洋,买了一台thinkpad-E450屏幕是16寸本,有AMD独立显卡,i5cpu,4G内存。 . 后来加了一个同型号4G内存组成双通道, . 加了一个三星固态500G, . 换了一个…...

Mysql运维篇(四) Xtarbackup--备份与恢复练习
一路走来,所有遇到的人,帮助过我的、伤害过我的都是朋友,没有一个是敌人。如有侵权,请留言,我及时删除! 前言 xtrabackup是Percona公司CTO Vadim参与开发的一款基于InnoDB的在线热备工具,具有…...

vue3 封装一个通用echarts组件
实现这个组件需要引入echarts和vue-echarts插件,使用vue-echarts是因为它帮我们封装了一些很常用的功能,比如监听页面resize后重新渲染功能,本次组件只使用到了autoresize配置,其它可以根据官方文档按需选配 https://github.com/…...

安装 Windows Server 2003
1.镜像安装 镜像安装:Windows Server 2003 2.安装过程(直接以图的形式呈现) 按Enter(继续),继续后F8继续 直接Enter安装 下一步 秘钥:GM34K-RCRKY-CRY4R-TMCMW-DMDHM 等待安装成功即可...

在STM32中使用DMA进行SD卡读写操作的实现方法
在STM32中,使用DMA进行SD卡的读写操作可以提高数据传输的速度和效率。下面是在STM32中使用DMA进行SD卡读写操作的实现方法: ✅作者简介:热爱科研的嵌入式开发者,修心和技术同步精进 ❤欢迎关注我的知乎:对error视而不见…...
)
StringBuilder/StringBuffer类(Java)
StringBuilder/StringBuffer类 当对字符串进行修改的时候,使用 StringBuffer / StringBuilder 类更方便。和 String 类不同的是,StringBuffer 和 StringBuilder 类的对象能够被多次的修改,并且不产生新的未使用对象。方法类似 public class…...

SQL的1999语法
目录 交叉连接 实现交叉连接 自然连接 实现自然连接(实际上就是内连接) ON和USING 使用自然连接时要求两张表的字段名称相同,但是如果不相同或者两张表中有两组字段是重名,这时就要利用 ON 子句指定关联条件,利用 USING 子句…...

【AIGC】Stable Diffusion安装包
Stable Diffusion 的安装教程通常分为以下几个步骤: 一、安装 Python: 确保您的系统中已经安装了 Python,并且版本符合 Stable Diffusion 的要求。通常情况下,Python 版本应为 3.6 或更高版本。您可以从 Python 官方网站下载并安…...

C++:迭代器的封装思想
C:迭代器的封装思想 list迭代器实现反向迭代器实现 本博客将通过实现list的迭代器,以及它的反向迭代器,来帮助大家理解迭代器的底层逻辑,以及封装思想。 list迭代器实现 迭代器是一个遍历容器的工具,其可以通过自增自…...

飞天使-k8s知识点17-kubernetes实操2-pod探针的使用
文章目录 探针的使用容器探针启动实验1-启动探针的使用-startupprobeLiveness Probes 和 Readiness Probes演示若存在started.html 则进行 探针的使用 kubectl edit deploy -n kube-system corednslivenessprobe 的使用 livenessProbe:failureThreshold: 5httpGet:path: /heal…...

tee漏洞学习-翻译-3:TrustZone exploit for MSM8974
原文:http://bits-please.blogspot.com/2015/08/full-trustzone-exploit-for-msm8974.html 在这篇博文中,我们将介绍利用上一篇文章中描述的 TrustZone 漏洞的完整过程。 在开发此漏洞时,我只使用了我值得信赖的(个人࿰…...

rust递归遍历磁盘目录及文件
Std库实现 //遍历dir目录,找出修改日期距离当前超过age天的文件名称,存入file_list中 fn visit_dir(dir: &Path, file_list: &mut Vec<String>, age: u64) -> io::Result<()> {if dir.is_dir() {for entry in fs::read_dir(dir)…...
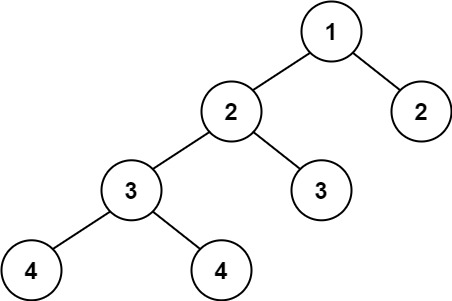
C语言每日一题(56)平衡二叉树
力扣网 110 平衡二叉树 题目描述 给定一个二叉树,判断它是否是高度平衡的二叉树。 本题中,一棵高度平衡二叉树定义为: 一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。 示例 1: 输入:root [3,9,20,…...
Flutter Android开发 梳理Google Material Design颜色体系
前言 做安卓开发(Kotlin语言),Flutter开发的人员应该都听说过谷歌一直推崇的Material Design,而Material Design Color是其推崇的颜色体系,具体来说,Material Design Color是一套旨在帮助设计师和开发者创…...

每日五道java面试题之java基础篇(六)
目录: 第一题:Java 创建对象有哪⼏种⽅式?第二题 .Integer a 127,Integer b 127;Integer c 128,Integer d 128;相等吗?第三题.Object 类的常⻅⽅法?第四题 List和Set的区别第五题 ArrayList和…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...
