蓝桥杯每日一题(python)
##斐波那契数列的应用 --- 题目斐波那契
题目:
如果数组 A = (a0, a1, · · · , an−1) 满足以下条件,就说它是一个斐波那契数组:
1. n ≥ 2;
2. a0 = a1;
3. 对于所有的 i(i ≥ 2),都满足 ai = ai−1 + ai−2。
现在,给出一个数组 A ,你可以执行任意次修改,每次修改将数组中的某个位置的元素修改为一个大于 0 的整数。请问最少修改几个元素之后,数组 A 会变成一个斐波那契数组。
输入格式
输入的第一行包含一个整数 n ,表示数组 A 中的元素个数。
第二行包含 n 个整数 a0, a1, · · · , an−1,相邻两个整数之间用一个空格分隔。
输出格式
输出一行包含一个整数表示最少需要修改数组 A 中的几个元素之后,数组 A 可以变为一个斐波那契数组。
样例输入
复制
5 1 2 2 4 8
样例输出
复制
3
提示
将原数组修改为 (1, 1, 2, 3, 5),最少修改三个元素变成了一个斐波那契数组。
对于所有评测用例,2 ≤ n ≤ 105 ,1 ≤ ai ≤ 106。
解题思路:我们枚举出前30个数的时候,发现第31个数已经超出了10的6次方,那么这后面的数全部都要修改,所以我们就不管30个以后的数了,我们的关注点就放在这30个。 然后我们发现,以下的式子都符合斐波那契数列的定义:
互相为倍数关系 1:1 1 2 3 5
2:2 2 4 6 10 3:3 3 6 9 15 则可以设计字典录入每层中有多少数,进行动态解题 循环每到一个数则对数取余看是否满足倍数关系,在对数取整存入 字典,最后利用数组长度减去倍数层最多的数,可得到需要修改的数。
注意事项: get函数的使用 --- 用在字典处
dict.get(key, default=None)
解释:
key:字典中要查找的键
default:键不存在时要返回的默认值,若不提供,则返回None
import os
import sysn = int(input()) # 接收数组长度
a = list(map(int, input().split())) # 输入的要修改的数组nums = [1, 1]
for i in range(1, 29):nums.append(nums[i - 1] + nums[i]) # 枚举出前30个斐波那契数列r = [] # 接收nums / a 的倍率
for i in range(min(len(a), len(nums))):r.append(nums[i] / a[i])res = 0 # 统计数目 符合的数
di = {} # 建立一个字典,以分层不同的倍率层
for j in r:di[j] = di.get(j, 0) + 1 # 不断增加个数res = max(di[j], res)print(len(a) - res) # 减去倍率层中数目最多的那个 就是最小要修改的数感谢你的观看。
相关文章:
)
蓝桥杯每日一题(python)
##斐波那契数列的应用 --- 题目斐波那契 题目: 如果数组 A (a0, a1, , an−1) 满足以下条件,就说它是一个斐波那契数组: 1. n ≥ 2; 2. a0 a1; 3. 对于所有的 i(i ≥ 2),都满足 ai ai−1 ai−2…...

【Vue】工程化开发脚手架Vue CLI
📝个人主页:五敷有你 🔥系列专栏:Vue⛺️稳重求进,晒太阳 工程化开发&脚手架Vue CLI 基本介绍 Vue Cli是Vue官方提供的一个全局命令工具 可以帮助我们快速创建一个开发Vue项目的标准化基础架子【集成了we…...

嵌入式培训机构四个月实训课程笔记(完整版)-Linux ARM驱动编程第三天-ARM Linux ADC和触摸屏开发 (物联技术666)
链接:https://pan.baidu.com/s/1V0E9IHSoLbpiWJsncmFgdA?pwd1688 提取码:1688 教学内容: 1、ADC S3C2440的A/D转换器包含一个8通道的模拟输入转换器,可以将模拟输入信号转换成10位数字编码。 在A/D转换时钟频率为2.5MHz时&…...
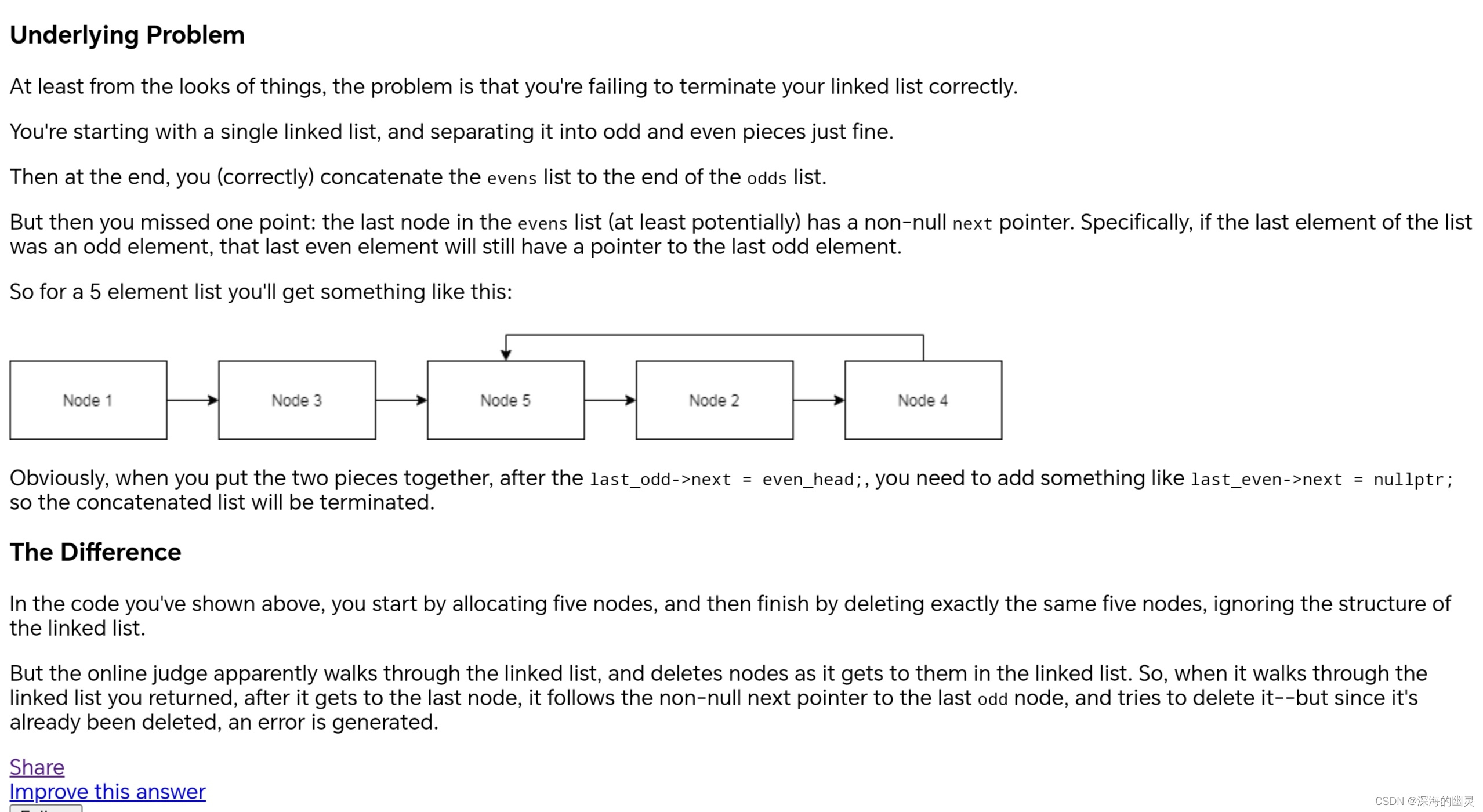
LeetCode “AddressSanitizer:heat-use-after-free on address“问题解决方法
heat-use-after-free : 访问堆上已经被释放的内存地址 现象:同样代码在LeetCode上报错,但是自己在IDE手动打印并不会报错 个人猜测,这个bug可能来源于LeetCode后台输出打印链表的代码逻辑问题。 问题描述 题目来自LeetCode的8…...

幸运彩票
L1-6 幸运彩票 分数 15 作者 陈越 单位 浙江大学 彩票的号码有 6 位数字,若一张彩票的前 3 位上的数之和等于后 3 位上的数之和,则称这张彩票是幸运的。本题就请你判断…...

搭建yum仓库服务器
安装 1.安装linux 1.1安装依赖 yum -y install gcc zlib zlib-devel pcre-devel openssl openssl-devel 1.2下载 cd /opt/nginx wget http://nginx.org/download/nginx-1.25.3.tar.gz 1.3解压 tar -xvf nginx-1.25.3.tar.gz 1.4配置 cd nginx-1.25.3 ./configure --pre…...

贪心算法练习day1
练习1--翻硬币 1)题目及要求 2)解题思路 输入的是字符串,要想将两组字符串进行一一对比,需要将字符串转换成字符数组,再使用for循环依次遍历字符数组,进行比对。 输入两行字符串,转换成两个字…...
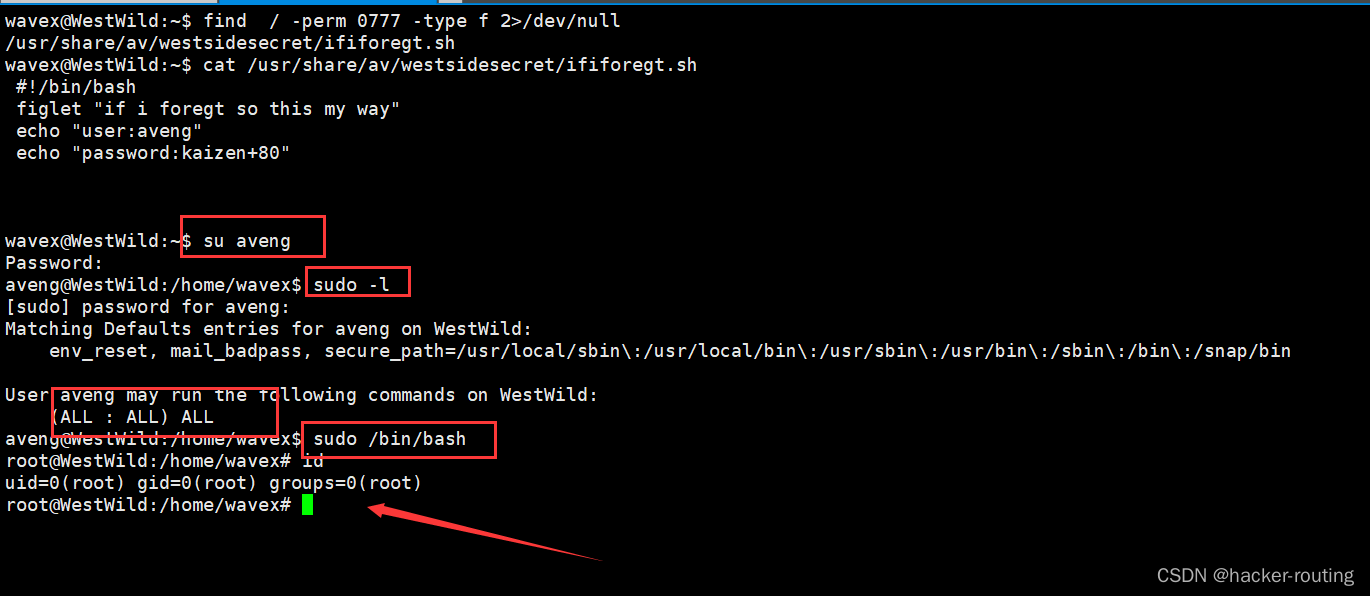
[VulnHub靶机渗透] WestWild 1.1
🍬 博主介绍👨🎓 博主介绍:大家好,我是 hacker-routing ,很高兴认识大家~ ✨主攻领域:【渗透领域】【应急响应】 【python】 【VulnHub靶场复现】【面试分析】 🎉点赞➕评论➕收藏…...

如何使用 ControlValueAccessor 在 Angular 中创建自定义表单控件
简介 在 Angular 中创建表单时,有时您希望拥有一个不是标准文本输入、选择或复选框的输入。通过实现 ControlValueAccessor 接口并将组件注册为 NG_VALUE_ACCESSOR,您可以将自定义表单控件无缝地集成到模板驱动或响应式表单中,就像它是一个原…...
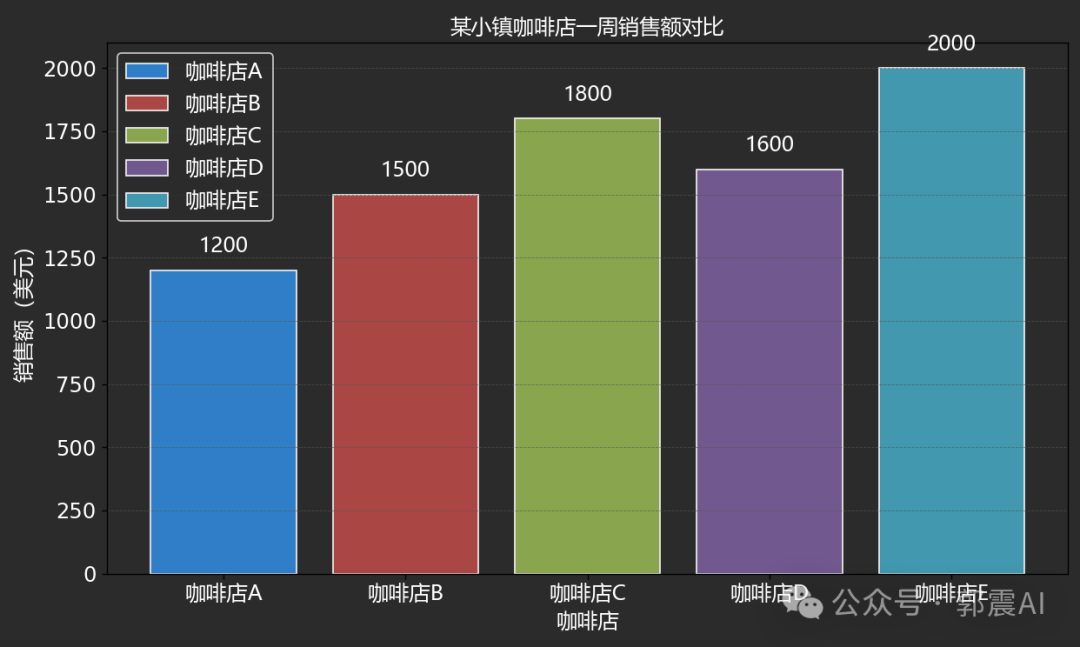
视频讲解:优化柱状图
你好,我是郭震 AI数据可视化 第三集:美化柱状图,完整视频如下所示: 美化后效果前后对比,前: 后: 附完整案例源码: util.py文件 import platformdef get_os():os_name platform.syst…...

OpenAI宣布ChatGPT新增记忆功能;谷歌AI助理Gemini应用登陆多地区
🦉 AI新闻 🚀 OpenAI宣布ChatGPT新增记忆功能,可以自由控制内存,提供个性化聊天和长期追踪服务 摘要:ChatGPT新增的记忆功能可以帮助AI模型记住用户的提问内容,并且可以自由控制其内存。这意味着用户不必…...

Solidworks:平面草图练习
继续练习平面草图,感觉基本入门了。...
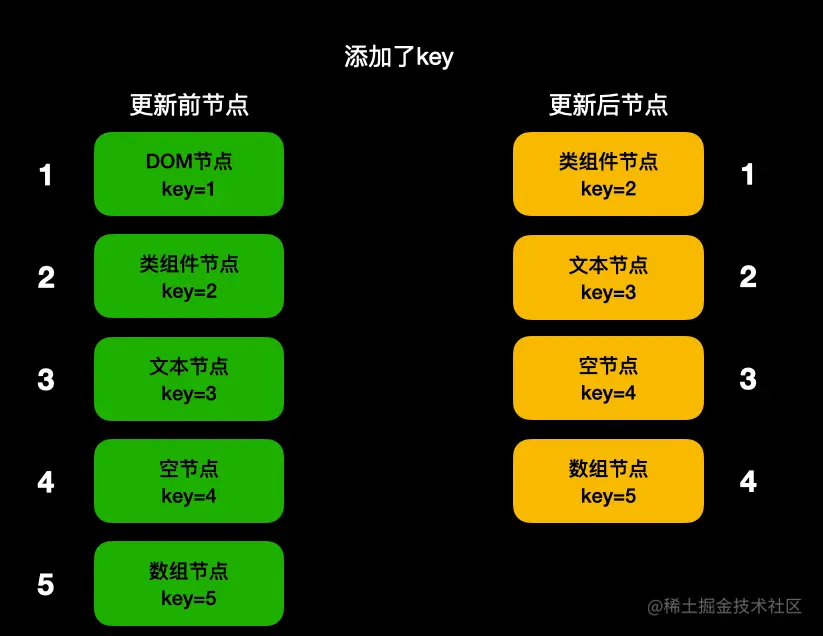
React18原理: 渲染与更新时的重点关注事项
概述 react 在渲染过程中要做很多事情,所以不可能直接通过初始元素直接渲染还需要一个东西,就是虚拟节点,暂不涉及React Fiber的概念,将vDom树和Fiber 树统称为虚拟节点有了初始元素后,React 就会根据初始元素和其他可…...
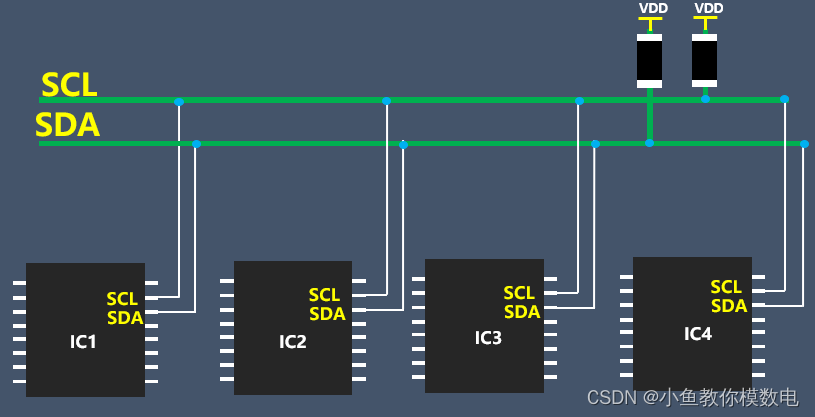
嵌入式I2C 信号线为何加上拉电阻(图文并茂)
IIC 是一个两线串行通信总线,包含一个 SCL 信号和 SDA 信号,SCL 是时钟信号,从主设备发出,SDA 是数据信号,是一个双向的,设备发送数据和接收数据都是通过 SDA 信号。 在设计 IIC 信号电路的时候我们会在 SC…...
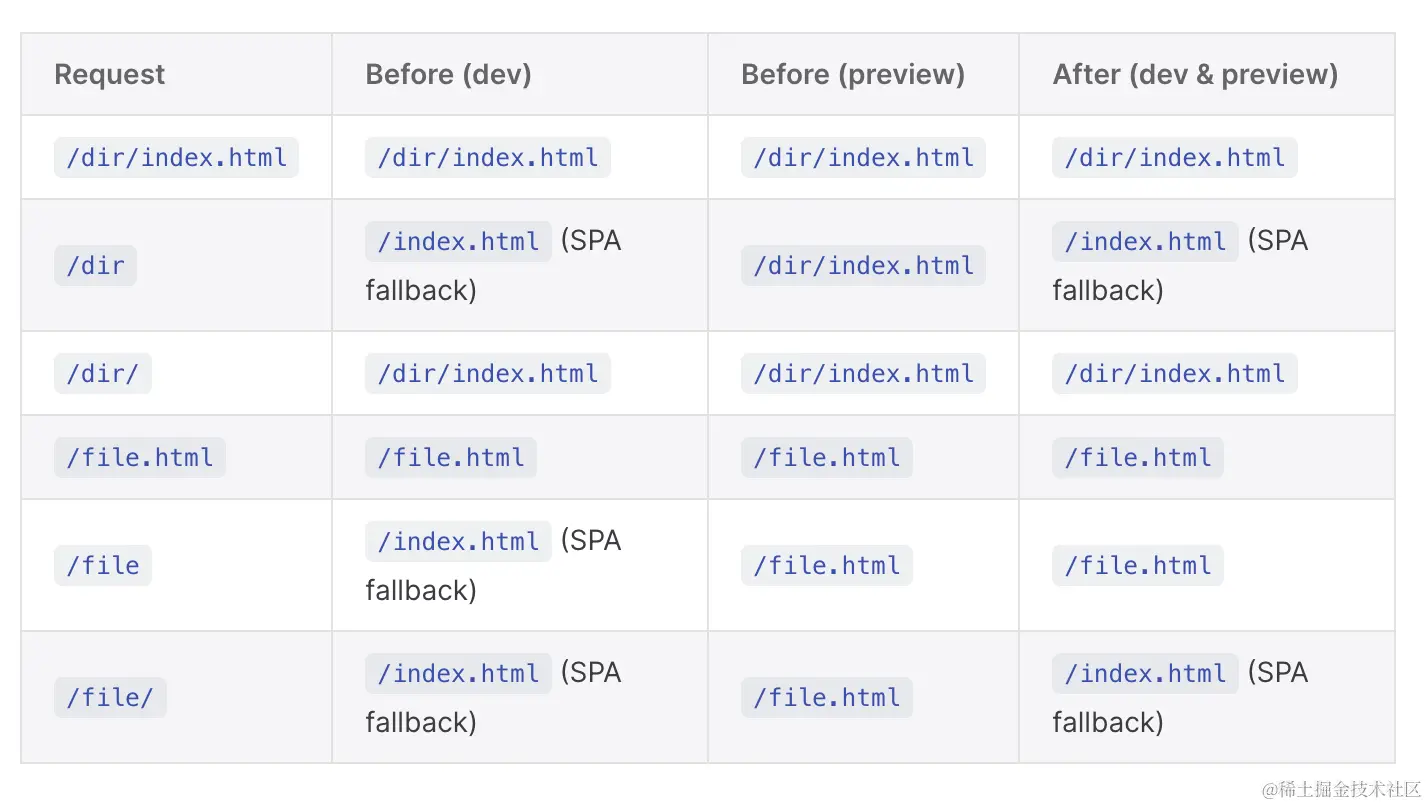
Vite 5.0 正式发布
11 月 16 日,Vite 5.0 正式发布,这是 Vite 道路上的又一个重要里程碑!Vite 现在使用 Rollup 4,这已经代表了构建性能的大幅提升。此外,还有一些新的选项可以改善开发服务器性能。 Vite 4 发布于近一年前,它…...
嵌入式STM32 单片机 GPIO 的工作原理详解
STM32的 GPIO 介绍 GPIO 是通用输入/输出端口的简称,是 STM32 可控制的引脚。GPIO 的引脚与外部硬件设备连接,可实现与外部通讯、控制外部硬件或者采集外部硬件数据的功能。 以 STM32F103ZET6 芯片为例子,该芯片共有 144 脚芯片,…...

系统调用的概念
在嵌入式开发、操作系统开发以及一般的系统编程中,系统调用是一个核心概念。它允许用户空间程序请求内核执行某些操作,如打开文件、读写数据、创建进程等。这些操作通常需要特殊的权限或访问硬件资源,因此不能直接在用户模式下执行。 系统调…...
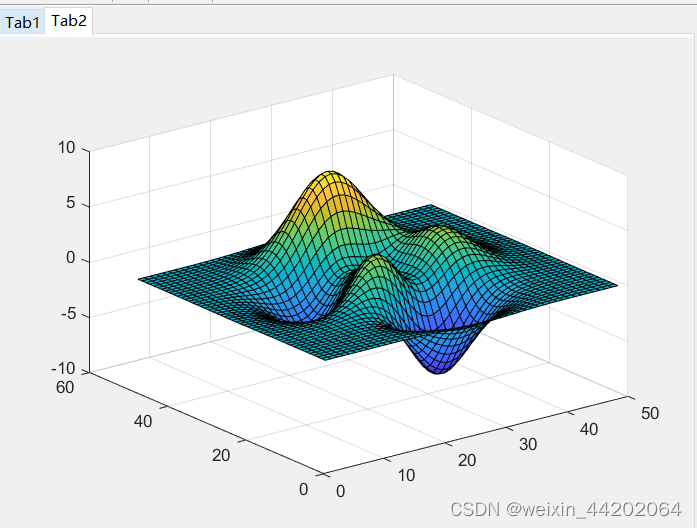
【无标题】Matlab 之axes函数——创建笛卡尔坐标区
**基本用法:**axes 在当前图窗中创建默认的笛卡尔坐标区,并将其设置为当前坐标区。 应用场景1:在图窗中放置两个 Axes 对象,并为每个对象添加一个绘图。 要求1:指定第一个 Axes 对象的位置,使其左下角位于…...

2.12:C语言测试题
1.段错误:申请堆区内存未返回,str指向NULL 2.段错误:局部变量,本函数结束,p也释放 3.越界访问,可能正常输出hello,可能报错 4.可能段错误,释放后,str未指向NULL&#x…...

【Linux】yum软件包管理器
目录 Linux 软件包管理器 yum 什么是软件包 Linux安装软件 查看软件包 关于rzsz Linux卸载软件 查看yum源 扩展yum源下载 Linux开发工具 vim编辑器 上述vim三种模式之间的切换总结: 命令模式下,一些命令: vim配置 Linux 软件包管理…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

HTTPS证书一年多少钱?
HTTPS证书作为保障网站数据传输安全的重要工具,成为众多网站运营者的必备选择。然而,面对市场上种类繁多的HTTPS证书,其一年费用究竟是多少,又受哪些因素影响呢? 首先,HTTPS证书通常在PinTrust这样的专业平…...
