数据结构:4_二叉树
二叉树
一.树概念及结构
1. 树的概念
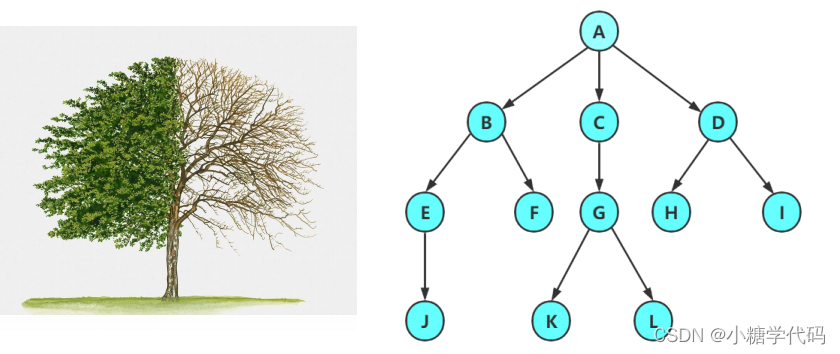
树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。
-
有一个**特殊的结点，称为根结点，**根节点没有前驱结点
-
除根节点外，其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm，其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱，可以有0个或多个后继
-
因此，树是递归定义的。
-
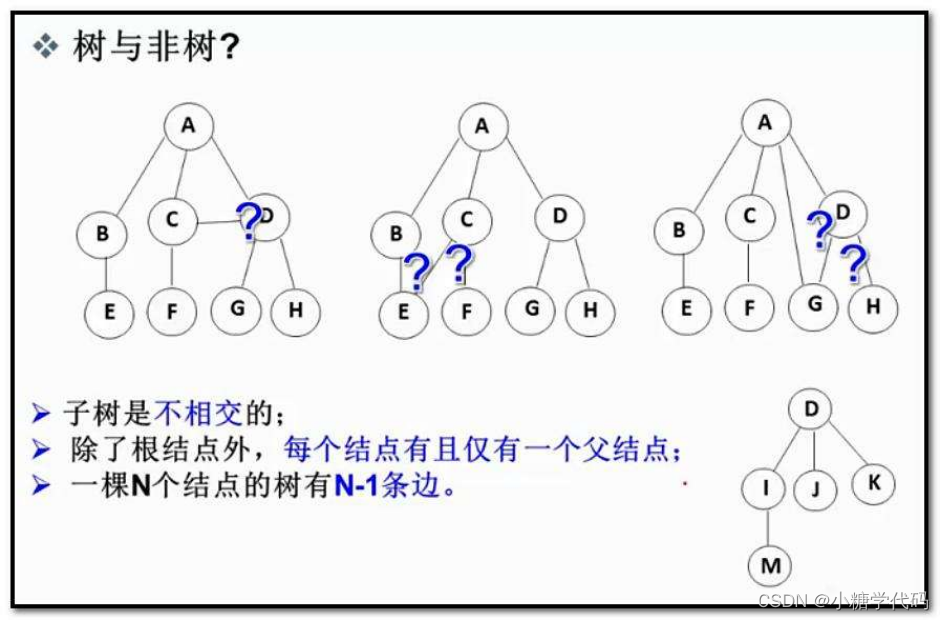
注意：树形结构中，子树之间不能有交集，否则就不是树形结构
2. 树的相关概念
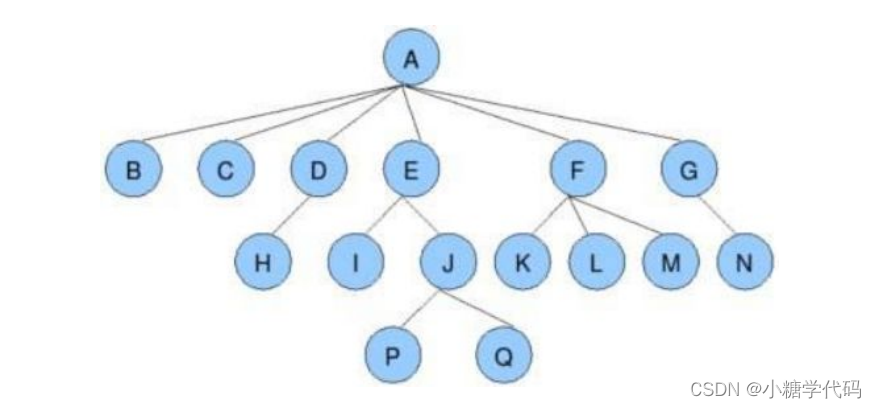
- 节点的度：一个节点含有的子树的个数称为该节点的度； 如上图：A的为6
- 叶节点或终端节点：度为0的节点称为叶节点； 如上图：B、C、H、I…等节点为叶节点
- 非终端节点或分支节点：度不为0的节点； 如上图：D、E、F、G…等节点为分支节点
- 双亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点； 如上图：A是B的父节点
- 孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点； 如上图：B是A的孩子节点
- 兄弟节点：具有相同父节点的节点互称为兄弟节点； 如上图：B、C是兄弟节点
- 树的度：一棵树中，最大的节点的度称为树的度； 如上图：树的度为6
- 节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；
- 树的高度或深度：树中节点的最大层次； 如上图：树的高度为4
- 堂兄弟节点：双亲在同一层的节点互为堂兄弟；如上图：H、I互为兄弟节点
- 节点的祖先：从根到该节点所经分支上的所有节点；如上图：A是所有节点的祖先
- 子孙：以某节点为根的子树中任一节点都称为该节点的子孙。如上图：所有节点都是A的子孙
- 森林：由m（m>0）棵互不相交的树的集合称为森林；
3. 树的表示
树结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了，既然保存值域，也要保存结点和结点之间的关系，实际中树有很多种表示方式如：双亲表示法，孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一个孩子结点struct Node* _pNextBrother; // 指向其下一个兄弟结点DataType _data; // 结点中的数据域
};
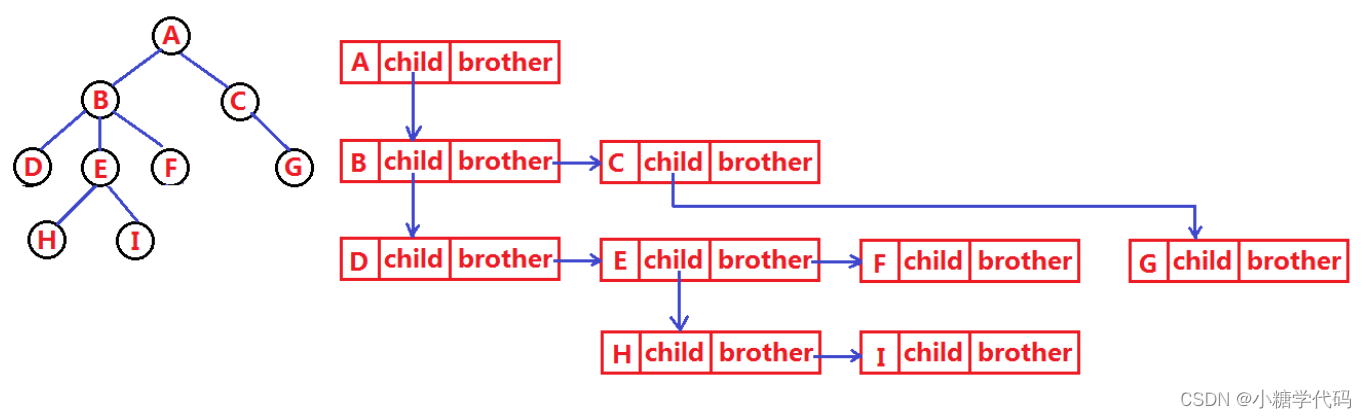
- 改方法是最优方法
- 初次之外还有两种方法表示树
4. 树在实际中的运用（表示文件系统的目录树结构）
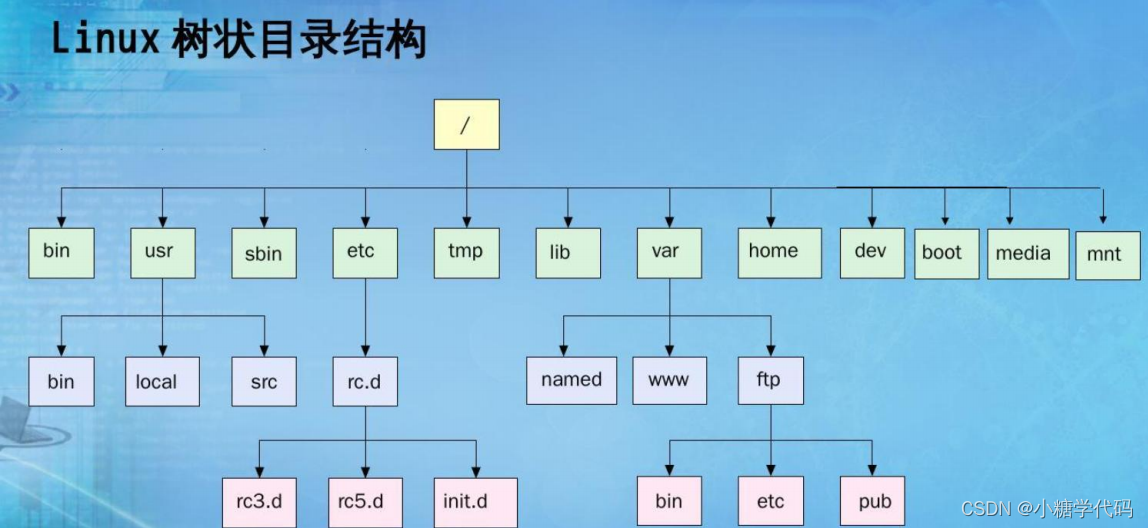
二.二叉树概念及结构
1. 概念
-
一棵二叉树是结点的一个有限集合，该集合:
- (1). 或者为空
- (2). 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
-
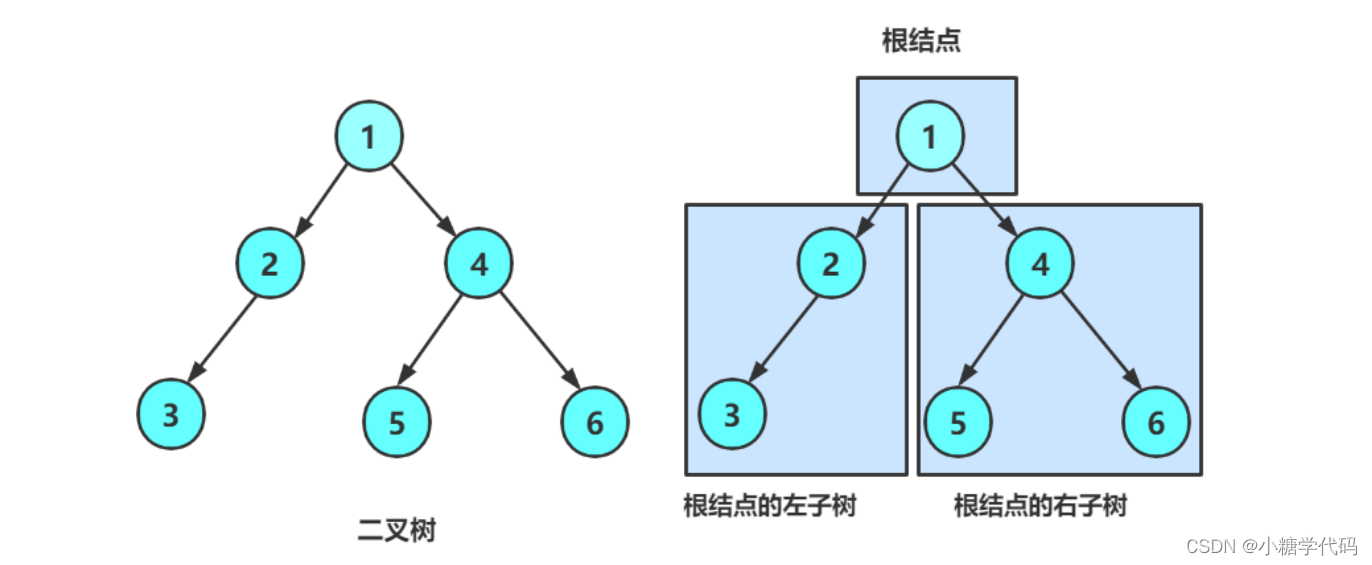
从上图可以看出：
- (1). 二叉树不存在度大于2的结点
- (2). 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树
-
注意：对于任意的二叉树都是由以下几种情况复合而成的：
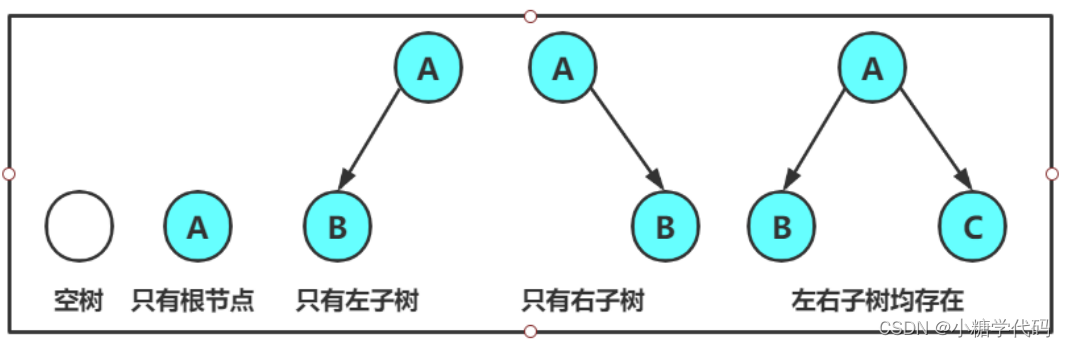
2. 特殊的二叉树：
(1). 满二叉树：
一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是2k-1 ，则它就是满二叉树。
(2). 完全二叉树：
完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。(即:前h-1层是满的，最后一层不一定满，但是从左到右必须连续)
3. 二叉树的性质
- (1). 若规定根节点的层数为1，则一棵非空二叉树的第i层上最多有2(i-1)个结点.
- (2). 若规定根节点的层数为1，则深度为h的二叉树的最大结点数是2h - 1.
- (3). 对任何一棵二叉树, 如果度为0其叶结点个数为n0, 度为2的分支结点个数为n2,则有n0＝n2＋1
- (4). 若规定根节点的层数为1，具有n个结点的满二叉树的深度，h=log2(n+1). (ps：log2(n+1)是log以2为底，n+1为对数)
- (5). 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的数组顺序对所有节点从0开始编号，则对于序号为i的结点有：
- ①. 若i>0，i位置节点的双亲序号：(i-1)/2；i=0，i为根节点编号，无双亲节点
- ②. 若2i+1<n，左孩子序号：2i+1，2i+1>=n否则无左孩子
- ③. 若2i+2<n，右孩子序号：2i+2，2i+2>=n否则无右孩子
1. 某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为（ ）
A 不存在这样的二叉树
B 200
C 198
D 199
2.下列数据结构中，不适合采用顺序存储结构的是（ ）
A 非完全二叉树
B 堆
C 队列
D 栈
3.在具有 2n 个结点的完全二叉树中，叶子结点个数为（ ）
A n
B n+1
C n-1
D n/2
4.一棵完全二叉树的节点数位为531个，那么这棵树的高度为（ ）
A 11
B 10
C 8
D 12
5.一个具有767个节点的完全二叉树，其叶子节点个数为（）
A 383
B 384
C 385
D 386
答案：
1.B
2.A
3.A
4.B
5.B
4.二叉树的存储结构
二叉树一般可以使用两种结构存储，一种顺序结构，一种链式结构。
(1).顺序存储
顺序结构存储就是使用数组来存储，一般使用数组只适合表示完全二叉树，因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储，关于堆我们后面的章节会专门讲解。二叉树顺序存储在物理上是一个数组，在逻辑上是一颗二叉树。
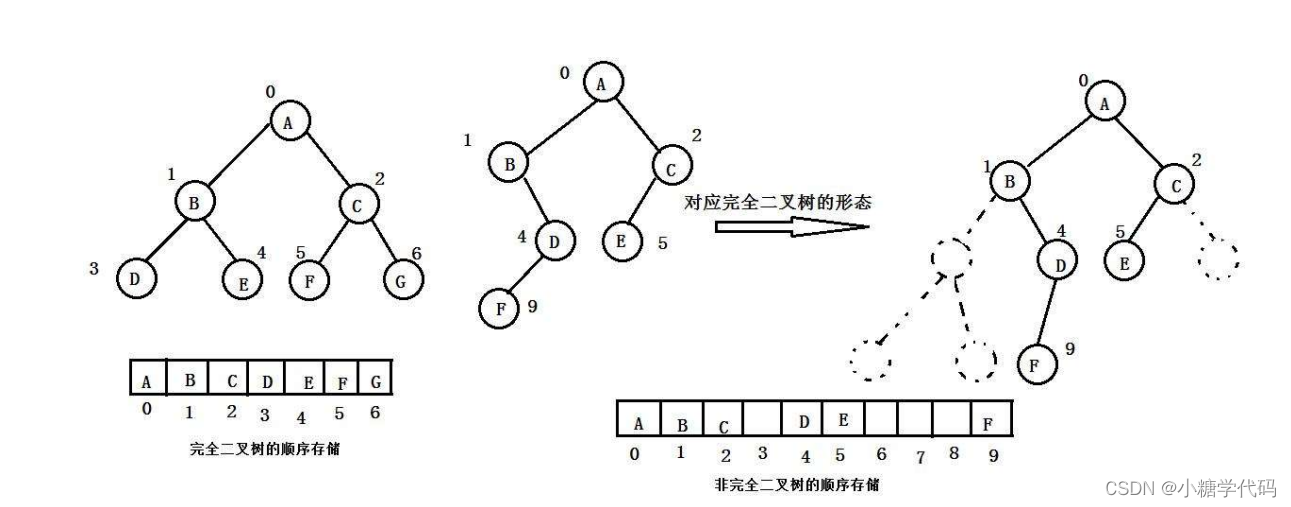
(2).链式存储
二叉树的链式存储结构是指，用链表来表示一棵二叉树，即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成，数据域和左右指针域，左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链，当前我们学习中一般都是二叉链，后面学到高阶数据结构如红黑树等会用到三叉链。
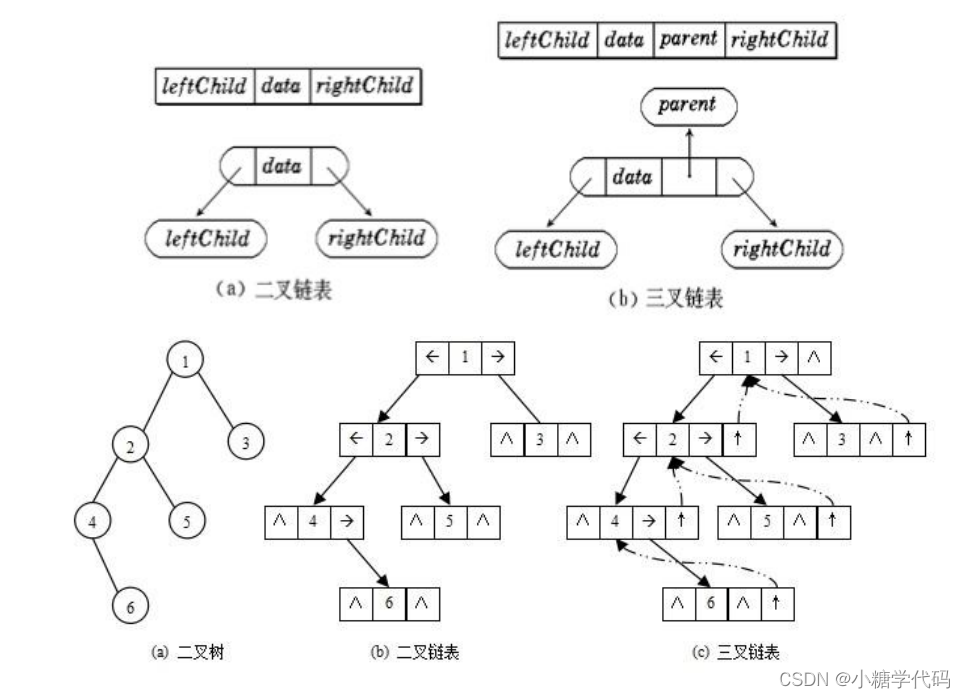
typedef int BTDataType;
// 二叉链
struct BinaryTreeNode
{struct BinTreeNode* _pLeft; // 指向当前节点左孩子struct BinTreeNode* _pRight; // 指向当前节点右孩子BTDataType _data; // 当前节点值域
}
// 三叉链
struct BinaryTreeNode
{struct BinTreeNode* _pParent; // 指向当前节点的双亲struct BinTreeNode* _pLeft; // 指向当前节点左孩子struct BinTreeNode* _pRight; // 指向当前节点右孩子BTDataType _data; // 当前节点值域
}；
三.二叉树的顺序结构及实现
1. 二叉树的顺序结构
普通的二叉树是不适合用数组来存储的，因为可能会存在大量的空间浪费。而完全二叉树更适合使用顺序结构存储。现实中我们通常把堆(一种二叉树)使用顺序结构的数组来存储，需要注意的是这里的堆和操作系统虚拟进程地址空间中的堆是两回事，一个是数据结构，一个是操作系统中管理内存的一块区域分段。
2. 堆的概念及结构
如果有一个关键码的集合K = {k0，k1，k2，…，kn-1}，把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中，并满足：Ki <= K2*i+1且 Ki <= K2*i+2( Ki >= K2*i+1且Ki >= K2*i+2 ) i = 0，1，2…，则称为小堆(或大堆)。将根节点最大的堆叫做最大堆或大根堆，根节点最小的堆叫做最小堆或小根堆。
-
堆的性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值；
- 堆总是一棵完全二叉树。
-
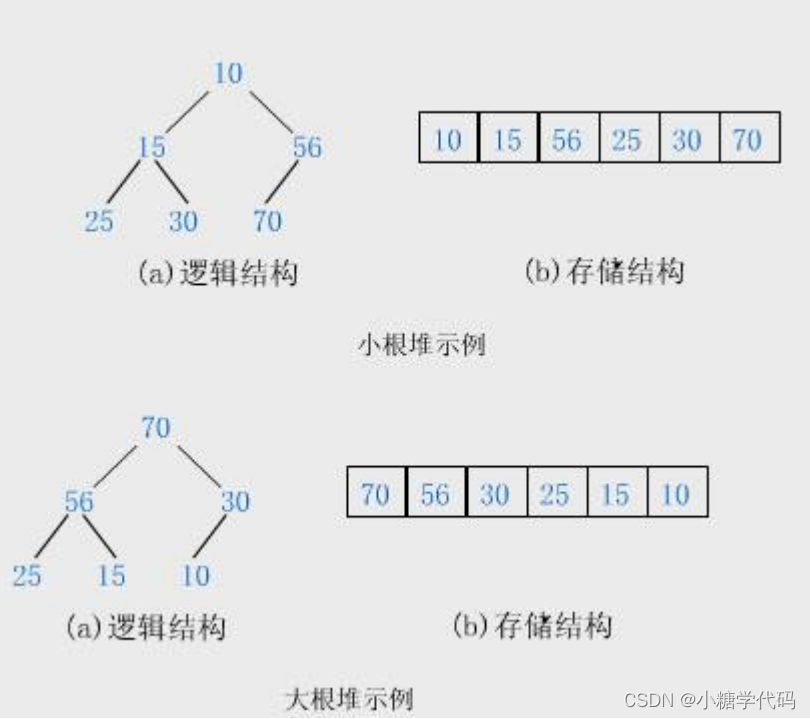
注意: 数据结构中的堆和C语言中的堆不一样
-
堆 – 数据结构 ~~~~~~~~~~ 完全二叉树
-
堆 – c语言/操作系统 ~~ 内存区域的划分
-
不同学科里面的同名名称
1.下列关键字序列为堆的是：（）
A 100,60,70,50,32,65
B 60,70,65,50,32,100
C 65,100,70,32,50,60
D 70,65,100,32,50,60
E 32,50,100,70,65,60
F 50,100,70,65,60,32
2.已知小根堆为8,15,10,21,34,16,12，删除关键字 8 之后需重建堆，在此过程中，关键字之间的比较次
数是（）。
A 1
B 2
C 3
D 4
3.一组记录排序码为(5 11 7 2 3 17),则利用堆排序方法建立的初始堆为
A(11 5 7 2 3 17)
B(11 5 7 2 17 3)
C(17 11 7 2 3 5)
D(17 11 7 5 3 2)
E(17 7 11 3 5 2)
F(17 7 11 3 2 5)
4.最小堆[0,3,2,5,7,4,6,8],在删除堆顶元素0之后，其结果是（）
A[3，2，5，7，4，6，8]
B[2，3，5，7，4，6，8]
C[2，3，4，5，7，8，6]
D[2，3，4，5，6，7，8]1.A
2.C
3.C
4.C
3. 堆的实现
(1).堆向下调整算法 前提：左右子树必须是一个堆
现在我们给出一个数组，逻辑上看做一颗完全二叉树。我们通过从根节点开始的向下调整算法可以把它调整成一个小堆。向下调整算法有一个前提：左右子树必须是一个堆，才能调整。
int array[] = {27,15,19,18,28,34,65,49,25,37};
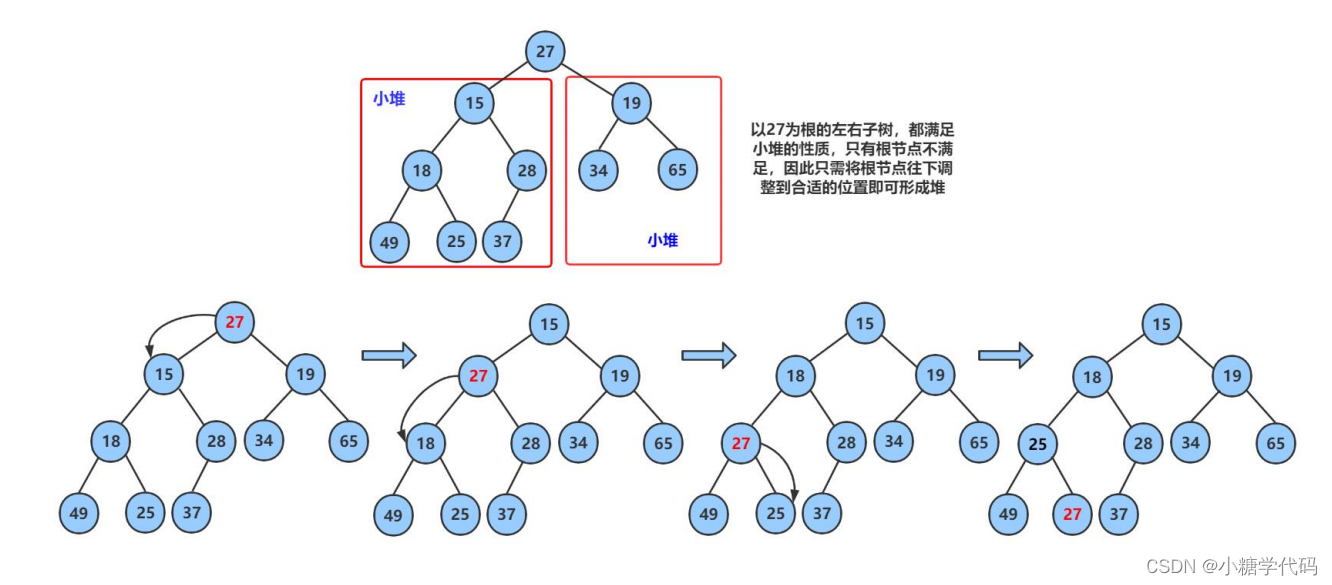
(2).堆的创建 将以有数组直接变成堆
下面我们给出一个数组，这个数组逻辑上可以看做一颗完全二叉树，但是还不是一个堆，现在我们通过算法，把它构建成一个堆。根节点左右子树不是堆，我们怎么调整呢？这里我们从倒数的第一个非叶子节点的子树开始调整，一直调整到根节点的树，就可以调整成堆。
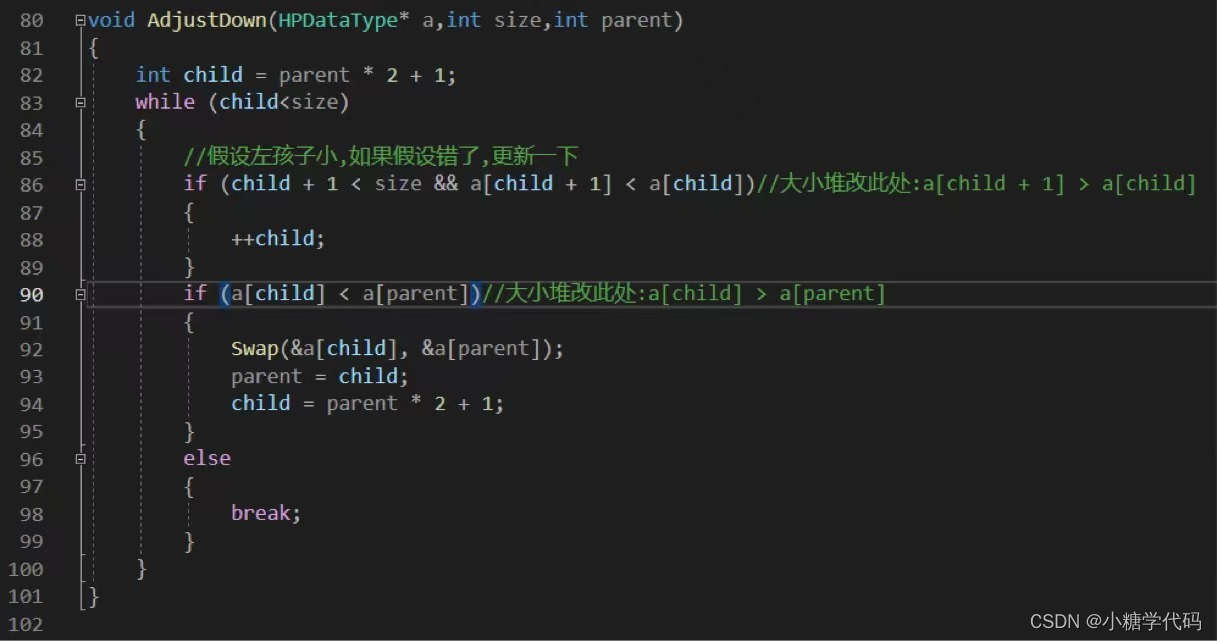
- 注意:一般建堆使用法2,其有两点优势:①时间复杂度小O(N)②只用写一个AdjustDown函数(堆排序后面一定要用)
(3).建堆时间复杂度
①向下调整建堆时间复杂度
- 因为堆是完全二叉树，而满二叉树也是完全二叉树，此处为了简化使用满二叉树来证明(时间复杂度本来看的就是近似值，多几个节点不影响最终结果)：
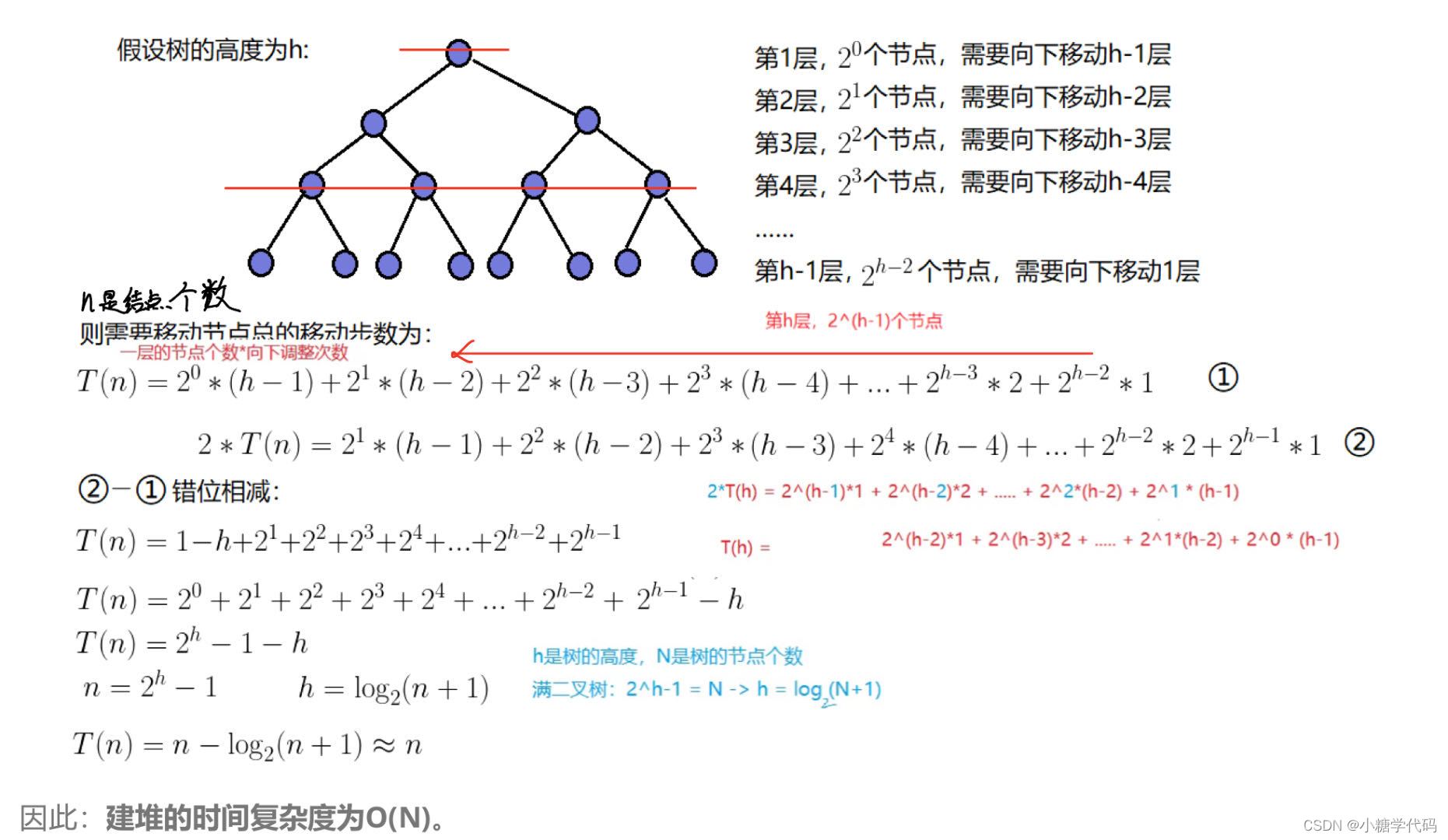
②向上调整建堆时间复杂度
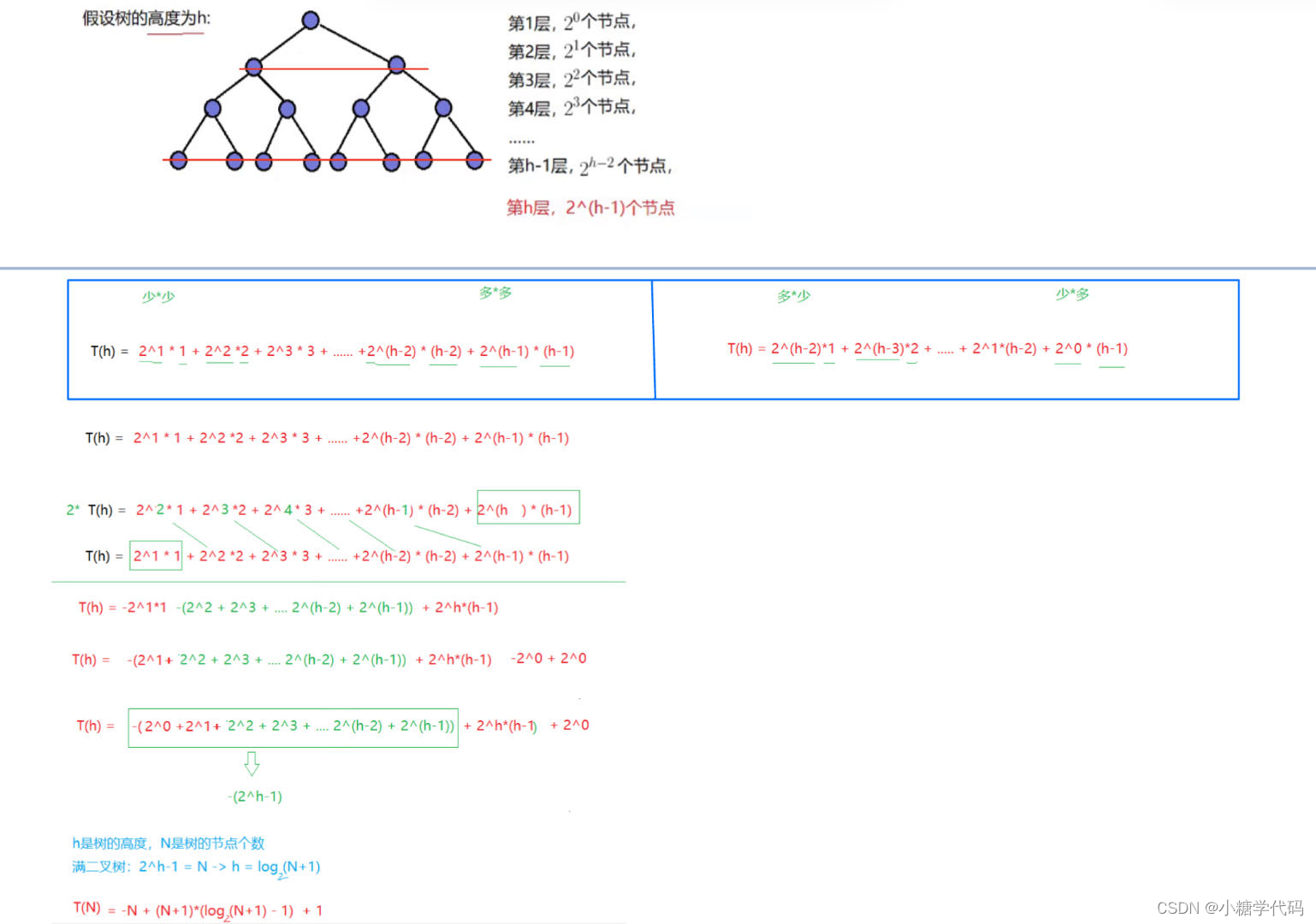
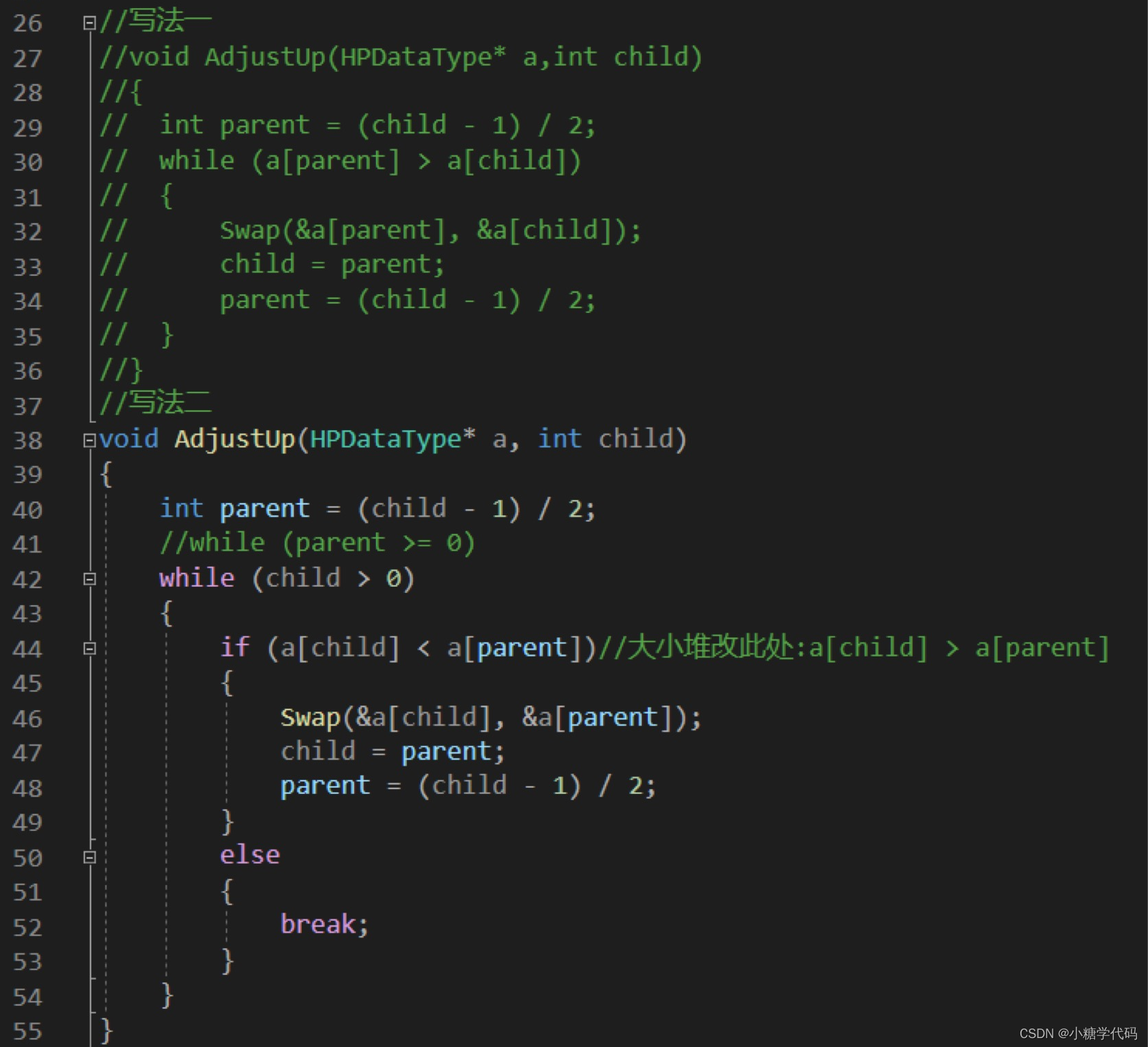
(4).堆的插入 向上调整的前提是前面的树构成堆
先插入一个10到数组的尾上，再进行向上调整算法，直到满足堆。
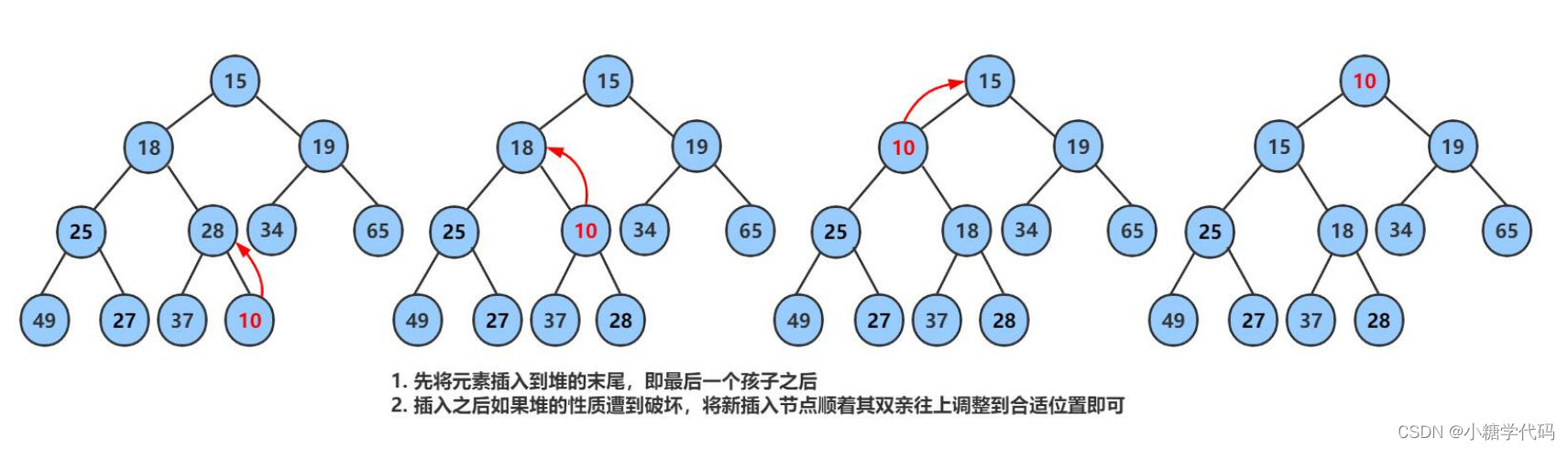
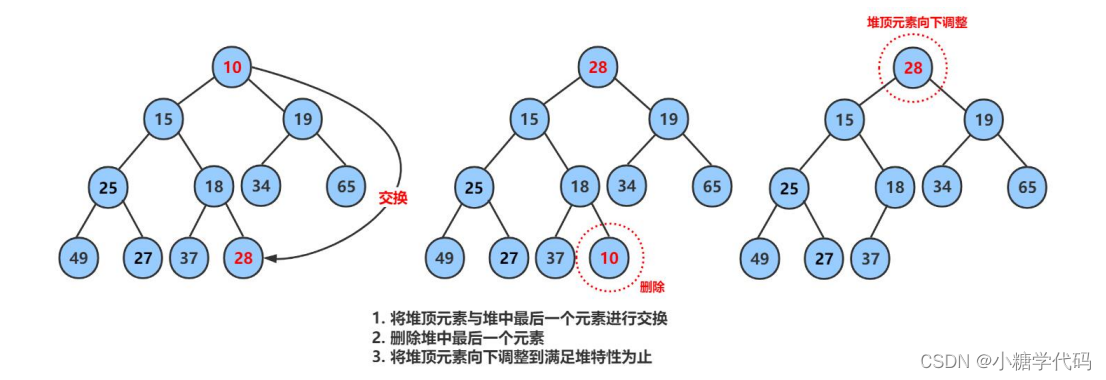
(5).堆的删除
删除堆是删除堆顶的数据，将堆顶的数据根最后一个数据一换，然后删除数组最后一个数据，再进行向下调整算法。
(6).堆的代码实现
typedef int HPDataType;
typedef struct Heap
{HPDataType* _a;int _size;int _capacity;
}Heap;
// 堆的构建
void HeapCreate(Heap* hp, HPDataType* a, int n);
// 堆的销毁
void HeapDestory(Heap* hp);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);
// 堆的删除
void HeapPop(Heap* hp);
// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
int HeapEmpty(Heap* hp);
//堆的实现
typedef int HPDataType;typedef struct Heap
{HPDataType* a;int size;int capacity;
}HP;//小堆
void HeapInit(HP* php)
{assert(php);php->a = NULL;php->capacity = 0;php->size = 0;
}void HeapDestory(HP* php)
{assert(php);free(php->a);php->a = NULL;php->capacity = php->size = 0;
}void Swap(HPDataType* p1, HPDataType* p2)
{HPDataType tmp = *p1;*p1 = *p2;*p2 = tmp;
}//写法一
//void AdjustUp(HPDataType* a,int child)
//{
// int parent = (child - 1) / 2;
// while (a[parent] > a[child])
// {
// Swap(&a[parent], &a[child]);
// child = parent;
// parent = (child - 1) / 2;
// }
//}
//写法二
void AdjustUp(HPDataType* a, int child)
{int parent = (child - 1) / 2;//while (parent >= 0)while (child > 0){if (a[child] < a[parent])//大小堆改此处:a[child] > a[parent]{Swap(&a[child], &a[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}//O(logN)
void HeapPush(HP* php, HPDataType x)
{assert(php);if (php->size == php->capacity){int newCapacity = php->capacity == 0 ? 4 : 2 * php->capacity;HPDataType* tmp = (HPDataType*)realloc(php->a, newCapacity * sizeof(HPDataType));if (tmp == NULL){perror("realloc fail");exit(-1);}php->a = tmp;php->capacity = newCapacity;}php->a[php->size] = x;php->size++;AdjustUp(php->a, php->size - 1);
}void AdjustDown(HPDataType* a,int size,int parent)
{int child = parent * 2 + 1;while (child<size){//假设左孩子小,如果假设错了,更新一下if (child + 1 < size && a[child + 1] < a[child])//大小堆改此处:a[child + 1] > a[child]{++child;}if (a[child] < a[parent])//大小堆改此处:a[child] > a[parent]{Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}}
}void HeapPop(HP* php)
{assert(php);assert(php->size > 0);Swap(&php->a[0], &php->a[php->size - 1]);php->size--;AdjustDown(php->a,php->size,0);
}HPDataType HeapTop(HP* php)
{assert(php);assert(php->size > 0);return php->a[0];
}int HeapSize(HP* php)
{assert(php);return php->size;
}bool HeapEmpty(HP* php)
{return php->size == 0;
}
4. 堆的应用
(1).堆排序–本质是一种选择排序
堆排序即利用堆的思想来进行排序，总共分为两个步骤：
-
- 建堆
- 升序：建大堆
- 降序：建小堆
-
- 利用堆删除思想来进行排序
建堆和堆删除中都用到了向下调整，因此掌握了向下调整，就可以完成堆排序。
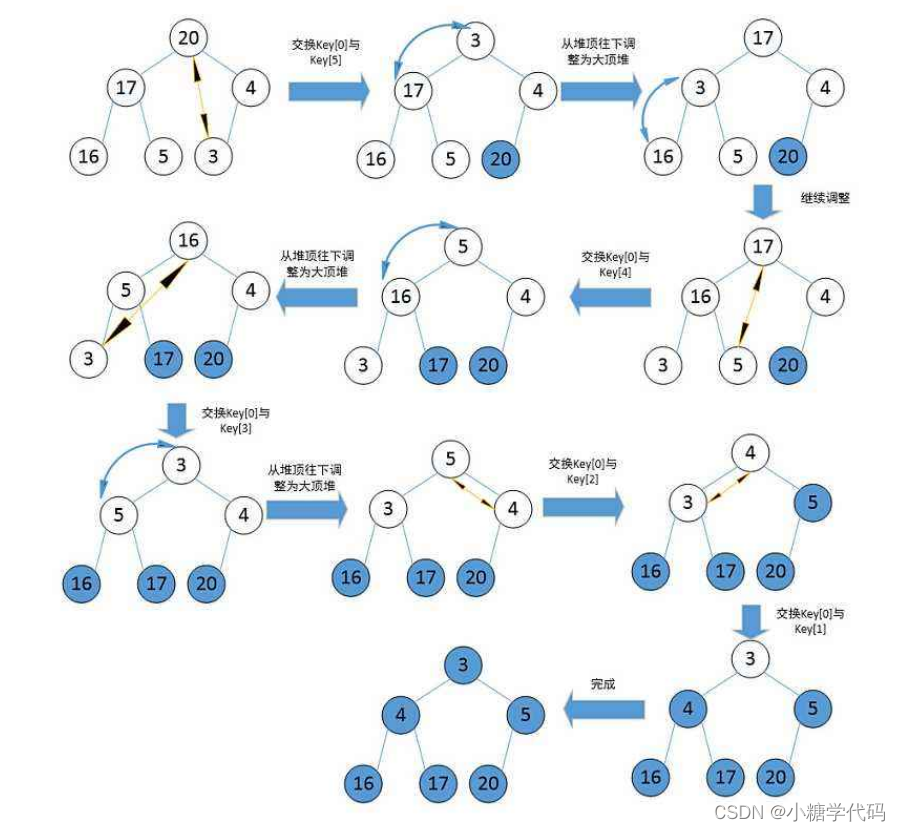
- 利用堆删除思想来进行排序
(2). TOP-K问题
TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。
比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决，基本思路如下：
-
- 用数据集合中前K个元素来建堆
- 前k个最大的元素，则建小堆
- 前k个最小的元素，则建大堆
-
- 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素
- 将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
void PrintTopK(int* a, int n, int k)
{// 1. 建堆--用a中前k个元素建堆// 2. 将剩余n-k个元素依次与堆顶元素交换，不满则则替换
}
void CreateNDate()
{//造数据int n = 10000000;srand(time(0));const char* file = "data.txt";FILE* fin = fopen(file, "w");if (fin == NULL){perror("fopen fail");return;}for (int i = 0; i < n; i++){int x = (rand()+i) % n;fprintf(fin, "%d\n", x);}fclose(fin);
}
//Topk问题
void PrintTopK(const char* file, int k)
{FILE* fout = fopen(file, "r");if (fout == NULL){perror("fopen fail");return;}//建堆int* minheap = (int*)malloc(sizeof(int) * k);if (minheap == NULL){perror("malloc fail");return;}//读取前k个数据,建小堆for (int i = 0; i < k; i++){fscanf(fout, "%d", &minheap[i]);//%d后不用写/nAdjustUp(minheap, i);}int x = 0;while (fscanf(fout, "%d", &x)!=EOF)//%d后不用写/n{if (x > minheap[0]){minheap[0] = x;AdjustDown(minheap, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", minheap[i]);}free(minheap);fclose(fout);
}
int main()
{//CreateNDate();PrintTopK("data.txt", 5);return 0;
}
四.二叉树链式结构的实现
1. 前置说明
在学习二叉树的基本操作前，需先要创建一棵二叉树，然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入，为了降低大家学习成本，此处手动快速创建一棵简单的二叉树，快速进入二叉树操作学习，等二叉树结构了解的差不多时，我们反过头再来研究二叉树真正的创建方式。
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;
BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->_left = node2;node1->_right = node4;node2->_left = node3;node4->_left = node5;node4->_right = node6;return node1;
}
-
注意：上述代码并不是创建二叉树的方式，真正创建二叉树方式后序详解重点讲解。
-
再看二叉树基本操作前，再回顾下二叉树的概念，二叉树是：
- 1 . 空树
- 2 . 非空：根节点，根节点的左子树、根节点的右子树组成的。
-
从概念中可以看出，二叉树定义是递归式的，因此后序基本操作中基本都是按照该概念实现的。
2. 二叉树的遍历
(1).前序、中序以及后序遍历
学习二叉树结构，最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。
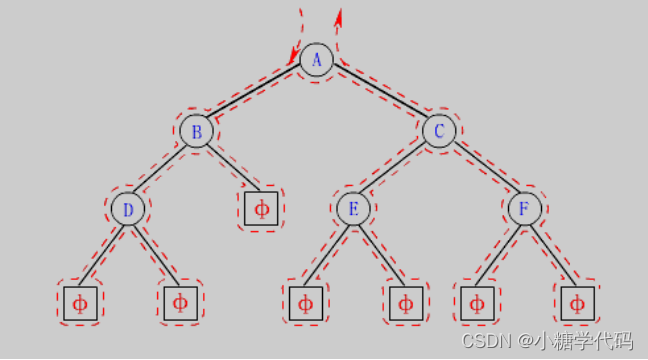
- 按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：
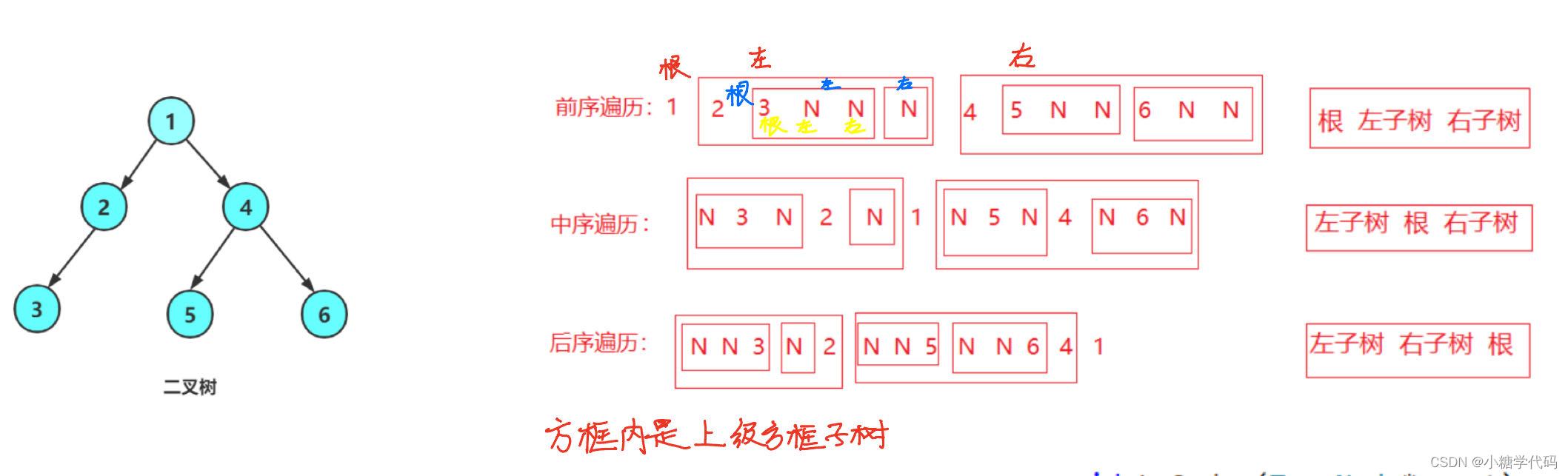
- 1.前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。[根 左子树 右子树]
- 2.中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。[左子树 根 右子树]
- 3.后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。[左子树 右子树 根]
也叫做先根,中根,后根遍历
由于被访问的结点必是某子树的根，所以N(Node）、L(Left subtree）和R(Right subtree）又可解释为根、根的左子树和根的右子树。 NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
// 二叉树前序遍历
void PreOrder(BTNode* root);
// 二叉树中序遍历
void InOrder(BTNode* root);
// 二叉树后序遍历
void PostOrder(BTNode* root);
//前序访问
void PrevOrder(TreeNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}//中序访问
void InOrder(TreeNode* root)
{if (root == NULL){printf("N ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}//后序访问
void PostOrder(TreeNode* root)
{if (root == NULL){printf("N ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}
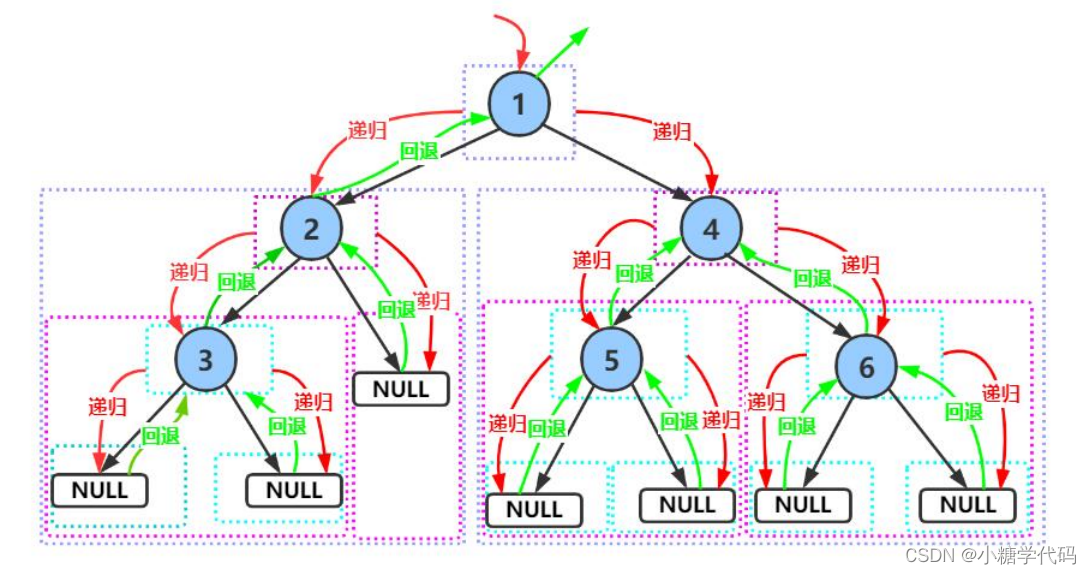
下面主要分析前序递归遍历，中序与后序图解类似，同学们可自己动手绘制。
前序遍历递归图解：
(2).层序遍历
void LevelOrder(TreeNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);int levelSize = 1;while (!QueueEmpty(&q)){//levelSize是每一层的数据个数，控制一层一层出// 一层一层出while (levelSize--){TreeNode* front = QueueFront(&q);QueuePop(&q);printf("%c ", front->data);//根据BTDataType选择打印格式if (front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);}printf("\n");levelSize = QueueSize(&q);}printf("\n");QueueDestroy(&q);
}
3. 节点个数以及高度等
- 注意:递归:
- 1.子问题分治
- 2.返回条件
// 1.二叉树节点个数
int TreeSize(TreeNode* root)
{return root == NULL ? 0 : 1 + TreeSize(root->left) + TreeSize(root->right);
}// 2.二叉树叶子节点个数
int TreeLeafSize(TreeNode* root)
{//空 返回0if (root == NULL)return 0;//不是空,是叶子 返回1if (root->left==NULL && root->right==NULL)return 1;//不是空 也不是叶子 分治=左右子树叶子之和 return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}// 补充:树的高度
//法一
int TreeHeight(TreeNode* root)
{if (root == NULL)return 0;int leftHeight = TreeHeight(root->left);int rightHeight = TreeHeight(root->right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}
//法二
int TreeHeight(TreeNode* root)
{if (root == NULL)return 0;return fmax(TreeHeight(root->left), TreeHeight(root->right))+1;
}// 3.二叉树第k层节点个数
int TreeLevelK(TreeNode* root, int k)
{assert(k > 0);if (root == NULL){return 0;}if (k == 1){return 1;}else{return TreeLevelK(root->left, k - 1) + TreeLevelK(root->right, k - 1);}
}// 4.二叉树查找值为x的节点
TreeNode* TreeFind(TreeNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->data == x)return root;TreeNode* left = TreeFind(root->left, x);if (left != NULL)return left;TreeNode* right = TreeFind(root->right, x);if (right != NULL)return right;return NULL;
}4. 二叉树基础oj练习
1. 单值二叉树
https://leetcode.cn/problems/univalued-binary-tree/
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/
bool isUnivalTree(struct TreeNode* root) {if(root==NULL)return true;if(root->left!=NULL&&root->left->val!=root->val)return false;if(root->right!=NULL&&root->right->val!=root->val)return false;return isUnivalTree(root->left)&&isUnivalTree(root->right);
}
2. 相同的树
https://leetcode.cn/problems/same-tree/submissions/
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {//都为空if(p==q)return true;//一个为空一个不为空if((p==NULL&&q!=NULL)||(p!=NULL&&q==NULL))//或者直接写(p=NULL||q==NULL)return false;//都不为空if(p->val!=q->val)return false;return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}
3. 对称二叉树
https://leetcode.cn/problems/symmetric-tree/
//法一:利用相同二叉树代码
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {//都为空if(p==q)return true;//一个为空一个不为空if((p==NULL&&q!=NULL)||(p!=NULL&&q==NULL))//或者直接写(p=NULL||q==NULL)return false;//都不为空if(p->val!=q->val)return false;return isSameTree(p->left,q->right)&&isSameTree(p->right,q->left);
}bool isSymmetric(struct TreeNode* root) {if(root==NULL)return true;return isSameTree(root->left,root->right);
}
//法二:新建子函数
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/
bool _isSymmetric(struct TreeNode* root1,struct TreeNode* root2) {if(root1==root2)return true;if(root1==NULL||root2==NULL)return false;if(root1->val!=root2->val)return false;return _isSymmetric(root1->left,root2->right)&&_isSymmetric(root1->right,root2->left);
}bool isSymmetric(struct TreeNode* root) {return _isSymmetric(root->left,root->right);
}
4. 二叉树的前序遍历
https://leetcode.cn/problems/binary-tree-preorder-traversal/description/
//法一:全局变量
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/
/*** Note: The returned array must be malloced, assume caller calls free().*/int i = 0;int TreeSize(struct TreeNode* root) {return root == NULL ? 0 : 1 + TreeSize(root->left) + TreeSize(root->right);
}void preorder(struct TreeNode* root, int* a) {if (root == NULL)return;a[i++] = root->val;preorder(root->left, a);preorder(root->right, a);
}// 输出型参数 (leetcode如果函数返回值是数组，不知道数组的大小。需要int* returnSize这样的输出型参数返回数组大小。)
int* preorderTraversal(struct TreeNode* root, int* returnSize) {int n = TreeSize(root);int* a = (int*)malloc(sizeof(int) * n);*returnSize = n;i = 0;preorder(root, a);return a;
}
//法二:局部变量
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/
/*** Note: The returned array must be malloced, assume caller calls free().*/int TreeSize(struct TreeNode* root) {return root == NULL ? 0 : 1 + TreeSize(root->left) + TreeSize(root->right);
}void preorder(struct TreeNode* root, int* a, int* pi) {if (root == NULL)return;a[(*pi)++] = root->val;preorder(root->left, a, pi);preorder(root->right, a, pi);
}// 输出型参数 (leetcode如果函数返回值是数组，不知道数组的大小。需要int*
// returnSize这样的输出型参数返回数组大小。)
int* preorderTraversal(struct TreeNode* root, int* returnSize) {int n = TreeSize(root);int* a = (int*)malloc(sizeof(int) * n);*returnSize = n;int i = 0;preorder(root, a,&i);return a;
}
5. 二叉树的中序遍历
https://leetcode.cn/problems/binary-tree-inorder-traversal/
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/
/*** Note: The returned array must be malloced, assume caller calls free().*/
int TreeSize(struct TreeNode* root)
{return root==NULL?0:1+TreeSize(root->left)+TreeSize(root->right);
}void inorder(struct TreeNode* root,int* a,int* pi)
{if(root==NULL)return;inorder(root->left,a,pi); a[(*pi)++]=root->val;inorder(root->right,a,pi);
}int* inorderTraversal(struct TreeNode* root, int* returnSize) {int n=TreeSize(root);*returnSize=n;int* a=(int*)malloc(sizeof(int)*n);int i=0;inorder(root,a,&i);return a;
}
6. 二叉树的后序遍历
https://leetcode.cn/problems/binary-tree-postorder-traversal/description/
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/
/*** Note: The returned array must be malloced, assume caller calls free().*/
int TreeSize(struct TreeNode* root)
{return root==NULL?0:1+TreeSize(root->left)+TreeSize(root->right);
}void postorder(struct TreeNode* root, int* a,int* pi)
{if(root==NULL)return;postorder(root->left,a,pi);postorder(root->right,a,pi);a[(*pi)++]=root->val;
}int* postorderTraversal(struct TreeNode* root, int* returnSize) {int n=TreeSize(root); *returnSize=n;int* a=(int*)malloc(sizeof(int)*n);int i=0;postorder(root,a,&i);return a;
}
7. 另一棵树的子树
https://leetcode.cn/problems/subtree-of-another-tree/description/
/*** Definition for a binary tree node.* struct TreeNode {* int val;* struct TreeNode *left;* struct TreeNode *right;* };*/
bool isSameTree(struct TreeNode* p, struct TreeNode* q) {//都为空if(p==q)return true;//一个为空一个不为空if((p==NULL&&q!=NULL)||(p!=NULL&&q==NULL))//或者直接写(p=NULL||q==NULL)return false;//都不为空if(p->val!=q->val)return false;return isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){if(isSameTree(root,subRoot))return true;if(root==NULL)return false;return isSubtree(root->left,subRoot)||isSubtree(root->right,subRoot);
}
5. 二叉树的创建和销毁
二叉树的构建及遍历。
https://www.nowcoder.com/practice/4b91205483694f449f94c179883c1fef?tpId=60&&tqId=29483&rp=1&ru=/activity/oj&qru=/ta/tsing-kaoyan/question-ranking
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
TreeNode* TreeCreate(char* a, int* pi)
// 二叉树销毁
void DestoryTree(TreeNode* root)
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);
// 1. 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
TreeNode* TreeCreate(char* a, int* pi)
{if (a[*pi] == '#'){(*pi)++;return NULL;}TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));if (root == NULL){perror("malloc fail");exit(-1);}root->data = a[(*pi)++];root->left = TreeCreate(a, pi);root->right = TreeCreate(a, pi);return root;
}
// 2. 二叉树销毁
void DestoryTree(TreeNode* root)//调用的人调用后自己把root置空
{if (root == NULL)return;DestoryTree(root->left);DestoryTree(root->right);free(root);return;
}
// 3. 是否是完全二叉树
bool TreeComplete(TreeNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){TreeNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL)break;QueuePush(&q, front->left);QueuePush(&q, front->right);}// 前面遇到空以后,后面还有非空就不是完全二叉树while (!QueueEmpty(&q)){TreeNode* front = QueueFront(&q);QueuePop(&q);if (front!=NULL)return false;}QueueDestroy(&q);return true;
}
五.总结
#pragma once
#include<stdio.h>
#include<stdbool.h>
#include<stdlib.h>
#include<assert.h>
#include<math.h>typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}TreeNode;// 1.前序访问
void PrevOrder(TreeNode* root);
// 2.中序访问
void InOrder(TreeNode* root);
// 3.后序访问
void PostOrder(TreeNode* root);
// 4.层序遍历
void LevelOrder(TreeNode* root);
// 5.二叉树销毁
void DestoryTree(TreeNode* root);
// 6.是否是完全二叉树
bool TreeComplete(TreeNode* root);// 1.节点个数
int TreeSize(TreeNode* root);
// 2.叶子节点的个数
int TreeLeafSize(TreeNode* root);
//补充:树的高度
int TreeHeight(TreeNode* root);
// 3.第k层结点个数
int TreeLevelK(TreeNode* root, int k);
// 4.查找值为x的结点
TreeNode* TreeFind(TreeNode* root, BTDataType x);// 通过前序遍历的数组构建二叉树
TreeNode* TreeCreate(BTDataType* a, int* pi);// 手撕二叉树
TreeNode* BuyTreeNode(int x);
TreeNode* CreateTree();
#include"BinaryTree.h"
#include"Queue.h"// 1.前序访问
void PrevOrder(TreeNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->data);//根据BTDataType选择打印格式PrevOrder(root->left);PrevOrder(root->right);
}
// 2.中序访问
void InOrder(TreeNode* root)
{if (root == NULL){printf("N ");return;}InOrder(root->left);printf("%d ", root->data);//根据BTDataType选择打印格式InOrder(root->right);
}
// 3.后序访问
void PostOrder(TreeNode* root)
{if (root == NULL){printf("N ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);//根据BTDataType选择打印格式
}// 4.层序遍历
void LevelOrder(TreeNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);int levelSize = 1;while (!QueueEmpty(&q)){//levelSize是每一层的数据个数，控制一层一层出// 一层一层出while (levelSize--){TreeNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->data);//根据BTDataType选择打印格式if (front->left)QueuePush(&q, front->left);if (front->right)QueuePush(&q, front->right);}printf("\n");levelSize = QueueSize(&q);}printf("\n");QueueDestroy(&q);
}// 5.二叉树销毁
void DestoryTree(TreeNode* root)//调用的人调用后自己把root置空
{if (root == NULL)return;DestoryTree(root->left);DestoryTree(root->right);free(root);return;
}// 6.是否是完全二叉树
bool TreeComplete(TreeNode* root)
{Queue q;QueueInit(&q);if (root)QueuePush(&q, root);while (!QueueEmpty(&q)){TreeNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL)break;QueuePush(&q, front->left);QueuePush(&q, front->right);}// 前面遇到空以后,后面还有非空就不是完全二叉树while (!QueueEmpty(&q)){TreeNode* front = QueueFront(&q);QueuePop(&q);if (front!=NULL)return false;}QueueDestroy(&q);return true;
}// 1.节点个数
int TreeSize(TreeNode* root)
{return root == NULL ? 0 : 1 + TreeSize(root->left) + TreeSize(root->right);
}// 2.叶子节点的个数
int TreeLeafSize(TreeNode* root)
{//空 返回0if (root == NULL)return 0;//不是空,是叶子 返回1if (root->left == NULL && root->right == NULL)return 1;//不是空 也不是叶子 分治=左右子树叶子之和 return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}//补充:树的高度
//法一
//int TreeHeight(TreeNode* root)
//{
// if (root == NULL)
// return 0;
// int leftHeight = TreeHeight(root->left);
// int rightHeight = TreeHeight(root->right);
// return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
//}
//法二
int TreeHeight(TreeNode* root)
{if (root == NULL)return 0;return fmax(TreeHeight(root->left), TreeHeight(root->right)) + 1;
}// 3.第k层结点个数
int TreeLevelK(TreeNode* root, int k)
{assert(k > 0);if (root == NULL){return 0;}if (k == 1){return 1;}else{return TreeLevelK(root->left, k - 1) + TreeLevelK(root->right, k - 1);}
}// 4.查找值为x的结点
TreeNode* TreeFind(TreeNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->data == x)return root;TreeNode* left = TreeFind(root->left, x);if (left != NULL)return left;TreeNode* right = TreeFind(root->right, x);if (right != NULL)return right;return NULL;
}// 通过前序遍历的数组构建二叉树
TreeNode* TreeCreate(BTDataType* a, int* pi)
{if (a[*pi] == -1)//a[*pi] == '#'{(*pi)++;return NULL;}TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));if (root == NULL){perror("malloc fail");exit(-1);}root->data = a[(*pi)++];root->left = TreeCreate(a, pi);root->right = TreeCreate(a, pi);return root;
}// 手撕二叉树
TreeNode* BuyTreeNode(int x)
{TreeNode* node = (TreeNode*)malloc(sizeof(TreeNode));assert(node);node->data = x;node->left = NULL;node->right = NULL;return node;
}TreeNode* CreateTree()
{TreeNode* node1 = BuyTreeNode(1);TreeNode* node2 = BuyTreeNode(2);TreeNode* node3 = BuyTreeNode(3);TreeNode* node4 = BuyTreeNode(4);TreeNode* node5 = BuyTreeNode(5);TreeNode* node6 = BuyTreeNode(6);TreeNode* node7 = BuyTreeNode(7);node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;node2->right = node7;return node1;
}
相关文章：
数据结构:4_二叉树
二叉树 一.树概念及结构 1. 树的概念 树是一种非线性的数据结构，它是由n（n>0）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。 有一个**特殊的…...
设计模式之：状态模式（State Pattern）
状态模式（State Pattern） 状态模式是一种行为设计模式，允许一个对象在其内部状态改变时改变它的行为。这种模式通过把状态的变化逻辑分布到State的子类之间，减少了相互间的依赖，使得状态的切换更加清晰。 状态模式的…...
【微服安全】API密钥和令牌与微服务安全的关系
什么是 API 密钥和令牌 API 密钥 API 密钥是一串用于识别应用程序或用户的字符串。它通常用于授权应用程序或用户访问 API。API 密钥可以是公开的，也可以是私有的。公开的 API 密钥可供任何人使用，而私有的 API 密钥只能由授权的应用程序或用户使用。 …...
Mock.js
在开发后端的应用中，我们使用postman来测试接口，观察和验证前后端之间的数据传递是否正常。 在开发前端的应用中，我们使用Mock.js来模拟后端服务，以便进行前端业务逻辑的开发和测试。 一般情况下，个人开发或者小团队开…...
【c++】list详细讲解
> 作者简介：დ旧言~，目前大二，现在学习Java，c，c，Python等 > 座右铭：松树千年终是朽，槿花一日自为荣。 > 目标：熟悉list库 > 毒鸡汤：你的脸上云淡…...
C#面：在.NET中 类 System.Web.UI.Page 可以被继承吗？
可以。 它是 ASP.NET WebForms中的一个重要类，用于表示 Web 页面。通过继承 System.Web.UI.Page 类，可以创建自定义的 Web 页面，并在其中添加自己的逻辑和功能。 继承 System.Web.UI.Page 类的好处是，可以重用和扩展已有的功能。…...
AI：128-基于机器学习的建筑物能源消耗预测
🚀点击这里跳转到本专栏，可查阅专栏顶置最新的指南宝典~ 🎉🎊🎉 你的技术旅程将在这里启航！ 从基础到实践，深入学习。无论你是初学者还是经验丰富的老手，对于本专栏案例和项目实践都有参考学习意义。 ✨✨✨ 每一个案例都附带有在本地跑过的关键代码，详细讲解供…...
php基础学习之可变函数（web渗透测试关键字绕过rce和回调函数）
可变函数 看可变函数的知识点之前，蒟蒻博主建议你先去看看php的可变变量，会更加方便理解，在本篇博客中的第五块知识点->php基础学习之变量-CSDN博客 描述 当一个变量所保存的值刚好是一个函数的名字（由函数命名规则可知该值必…...
MongoDB聚合操作符：$acos
$acos操作符返回一个值的反余弦。从MongoDB4.2版本开始支持。 语法 { $acos: <expression> }$acos接受任何可被解析为值在-1到1之间的表达式，即：-1 < value < 1$acos返回值以弧度为单位，使用$radiansToDegrees操作符可以把输出…...
开源PDF工具 Apache PDFBox 认识及使用(知识点+案例)
文章目录 前言源码获取一、认识PDFBox二、导入依赖三、基础功能demo1：读取pdf所有内容demo2：读取所有页内容（分页）demo3：添加页眉、页脚demo4：添加居中45文字水印demo5：添加图片到右上角 参考文…...
微软.NET6开发的C#特性——委托和事件
我是荔园微风，作为一名在IT界整整25年的老兵，看到不少初学者在学习编程语言的过程中如此的痛苦，我决定做点什么，下面我就重点讲讲微软.NET6开发人员需要知道的C#特性，然后比较其他各种语言进行认识。 C#经历了多年发展…...
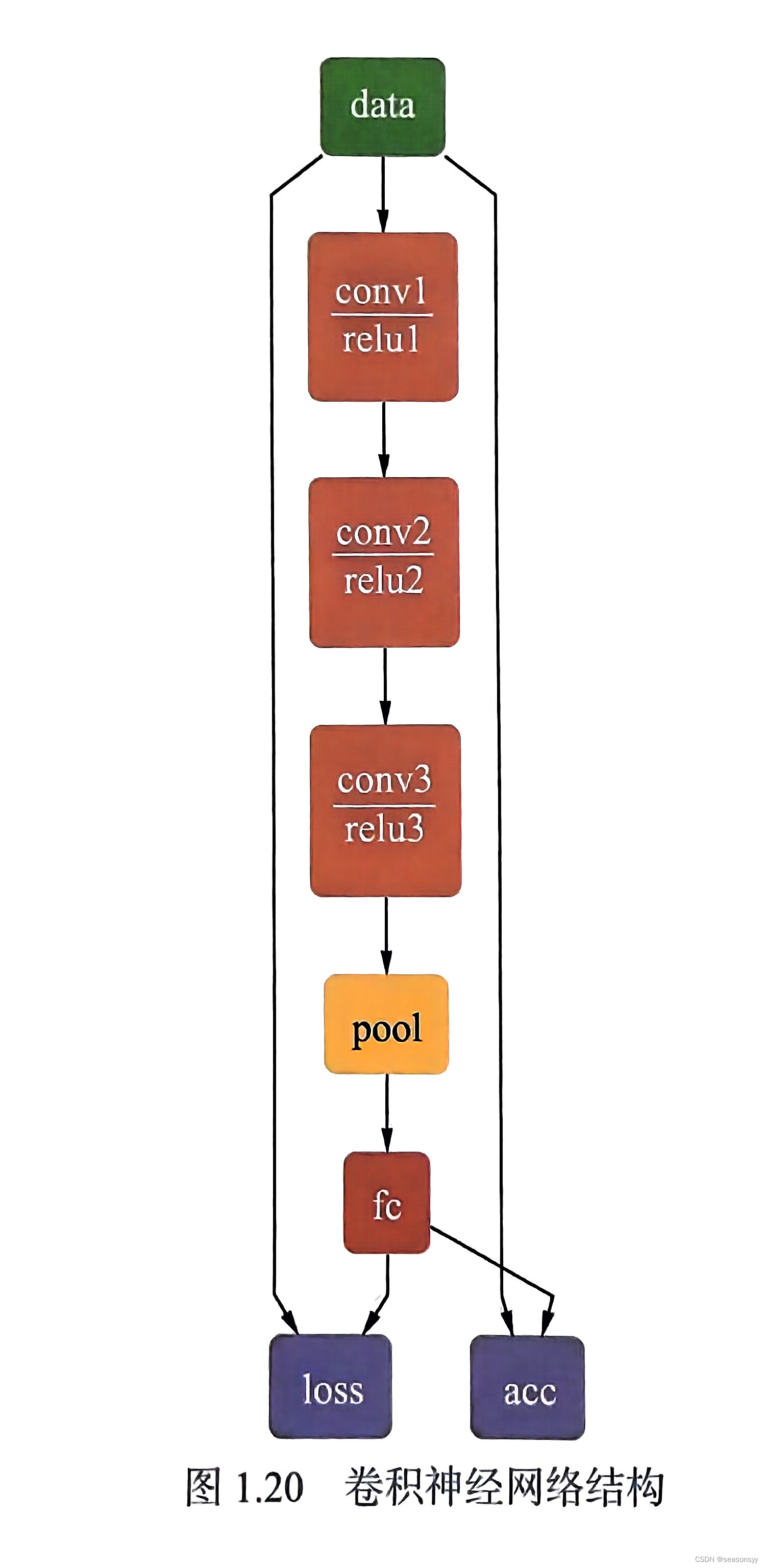
卷积神经网络的基本结构
卷积神经网络的基本结构 与传统的全连接神经网络一样，卷积神经网络依然是一个层级网络，只不过层的功能和形式发生了变化。 典型的CNN结构包括： 数据输入层（Input Layer）卷积层（Convolutional Layer&#x…...
python：使用GDAL库读取遥感影像指定行列数/经纬度坐标的像素值
作者：CSDN @ _养乐多_ 本文将介绍如何使用GDAL库来读取单波段遥感影像数据，如何获取指定行列位置的像素的经纬度坐标，并根据像素行列数或者经纬度坐标获取像素值。代码由python实现。 文章目录 一、读取影像二、获取指定行列位置的像素坐标三、根据地理坐标获取像素值四、根…...
Redis篇----第一篇
系列文章目录 文章目录 系列文章目录前言一、什么是 Redis?二、Redis 与其他 key-value 存储有什么不同？三、Redis 的数据类型？四、使用 Redis 有哪些好处？五、Redis 相比 Memcached 有哪些优势？前言 前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住…...
C语言-----用二维数组解决菱形的打印问题
1.打印菱形，多组输入，一个整数（2~20），表示输出的行数，也表示组成“X”的反斜线和正斜线的长度。 #include <stdio.h>int main() {int n0;while(scanf("%d",&n)! EOF){int i0;int j0;f…...
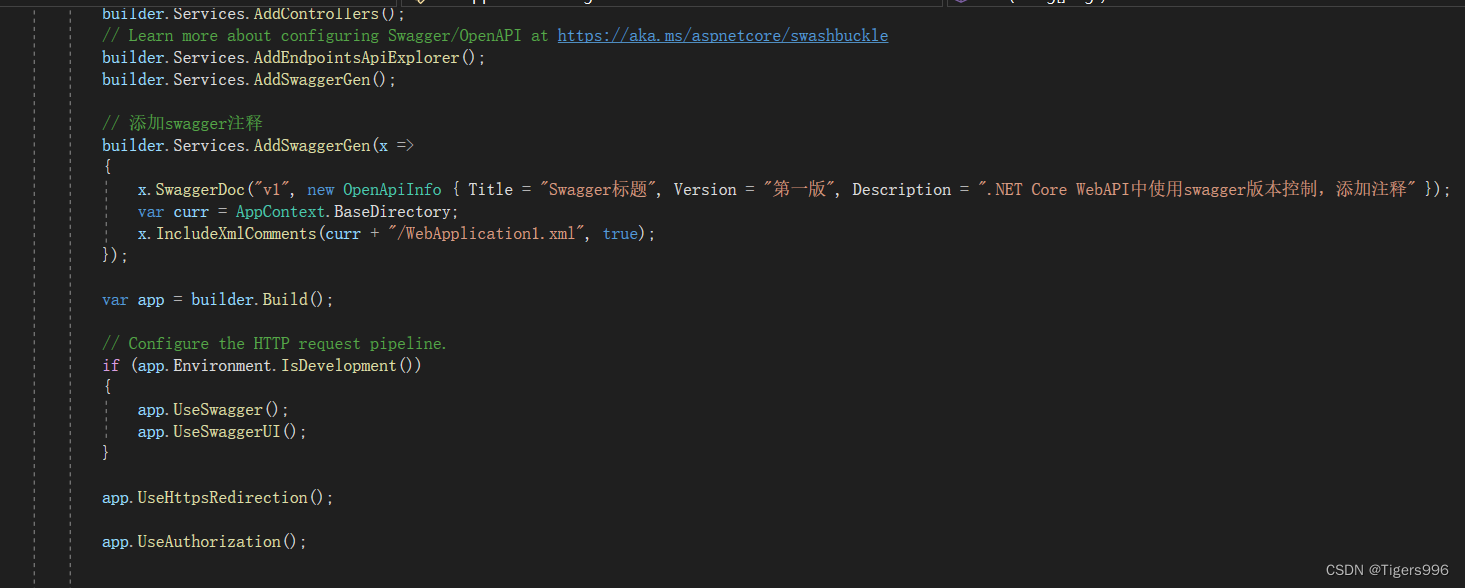
.NET Core WebAPI中使用swagger版本控制，添加注释
一、效果 二、实现步骤 在代码中添加注释 在项目属性中生成API文档 在Program中注册Swagger服务并配置文档信息 // 添加swagger注释 builder.Services.AddSwaggerGen(x > {x.SwaggerDoc("v1", new OpenApiInfo { Title "Swagger标题", Version "…...
css篇---移动端适配的方案有哪几种
移动端适配 移动端适配是指同一个页面可以在不同的移动端设备上都有合理的布局。主流实现的方案有 响应式布局通过rem或者vw,vh 等实现不同设备有相同的比例而实现适配 首先需要了解viewport 【视口】 视口代表了一个可看见的多边形区域（通常来说是矩形࿰…...
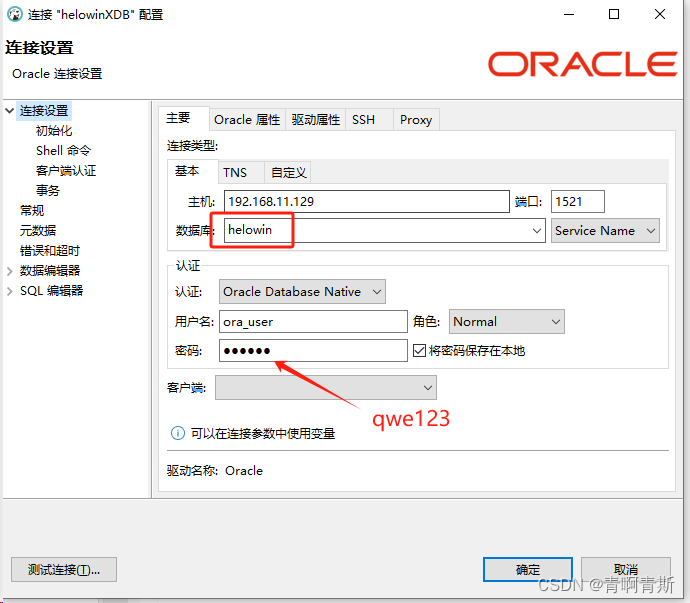
一、部署Oracle
部署Oracle 一、Docker部署1.Oracle11g1.1 测试环境1.1.1 拉取镜像1.1.2 启动容器1.1.3 配置容器环境变量1.1.4 修改sys、system用户密码1.1.5 创建表空间1.1.6 创建用户并授权1.1.5 使用DBeaver测试连接 二、安装包部署 一、Docker部署 1.Oracle11g 1.1 测试环境 当前只能用…...
11-编写自动化测试
上一篇： 10-通用类型、特质和生命周期 Edsger W. Dijkstra 在 1972 年发表的文章《The Humble Programmer》中说："程序测试可以非常有效地显示错误的存在，但对于显示错误的不存在却无能为力。这并不意味着我们不应该尽可能多地进行测试&…...
爱上JVM——常见问题（一）：JVM组成
1 JVM组成 1.1 JVM由那些部分组成，运行流程是什么？ 难易程度：☆☆☆ 出现频率：☆☆☆☆ JVM是什么 Java Virtual Machine Java程序的运行环境（java二进制字节码的运行环境） 好处： 一次编写&…...
未来机器人的大脑：如何用神经网络模拟器实现更智能的决策？
编辑：陈萍萍的公主一点人工一点智能 未来机器人的大脑：如何用神经网络模拟器实现更智能的决策？RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战，在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...
Spark 之 入门讲解详细版（1）
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室（Algorithms, Machines, and People Lab）开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目，8个月后成为Apache顶级项目，速度之快足见过人之处&…...
select、poll、epoll 与 Reactor 模式
在高并发网络编程领域，高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表，以及基于它们实现的 Reactor 模式，为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...
tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录，但是由于这个树组件的节点越来越多，导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多，导致的浏览器卡顿，这里很明显就需要用到虚拟列表的技术&…...
七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...
uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中，群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS，在uniapp中实现： 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...
mac：大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何，是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试，是可以跑通文章里面的代码。训练速度也是很快的。 注意…...
Vue 3 + WebSocket 实战：公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战：公司通知实时推送功能详解 📌 收藏 点赞 关注，项目中要用到推送功能时就不怕找不到了！ 实时通知是企业系统中常见的功能，比如：管理员发布通知后，所有用户…...
LUA+Reids实现库存秒杀预扣减 记录流水 以及自己的思考
目录 lua脚本 记录流水 记录流水的作用 流水什么时候删除 我们在做库存扣减的时候，显示基于Lua脚本和Redis实现的预扣减 这样可以在秒杀扣减的时候保证操作的原子性和高效性 lua脚本 // ... 已有代码 ...Overridepublic InventoryResponse decrease(Inventor…...
精益数据分析（98/126）：电商转化率优化与网站性能的底层逻辑
精益数据分析（98/126）：电商转化率优化与网站性能的底层逻辑 在电子商务领域，转化率与网站性能是决定商业成败的核心指标。今天，我们将深入解析不同类型电商平台的转化率基准，探讨页面加载速度对用户行为的…...