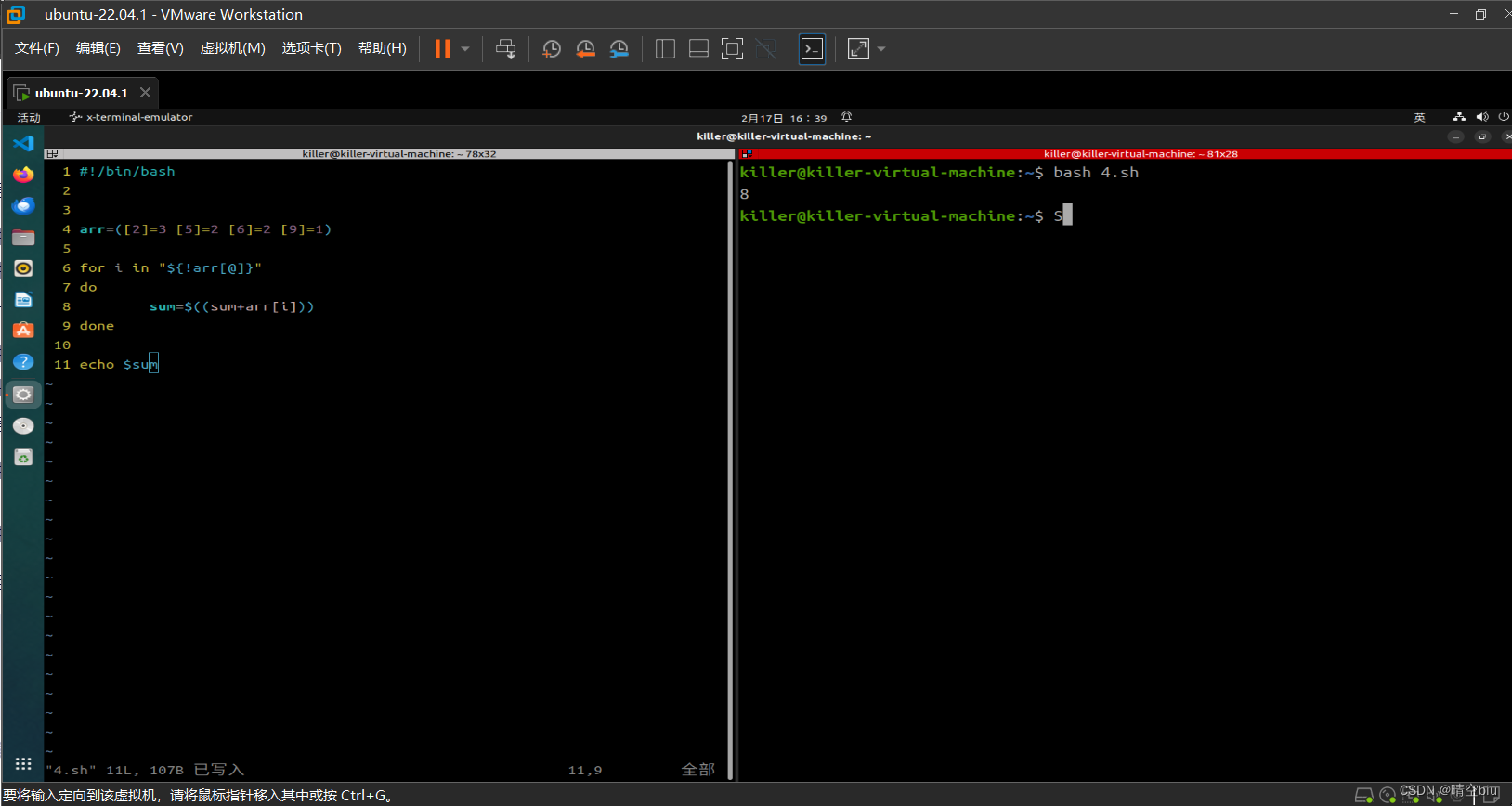
shell编程:求稀疏数组中元素的和(下标不连续)
#!/bin/basharr=([2]=3 [5]=2 [6]=2 [9]=1)for i in "${!arr[@]}"
dosum=$((sum+arr[i]))
doneecho $sum
Bash 脚本中,* 和 @ 符号在数组上下文中有不同的用途。当使用它们来遍历数组时,必须了解它们之间的区别。
*(无前置感叹号!):- 在索引数组(indexed array)中,
"${arr[*]}"会展开成数组中的所有元素。 - 在关联数组(associative array)中,
"${arr[*]}"是不合法的,因为关联数组没有连续的索引。
- 在索引数组(indexed array)中,
@(无前置感叹号!):- 在索引数组中,
"${arr[@]}"和"${arr[*]}"的功能相同,都会展开成数组中的所有元素。 - 在关联数组中,
"${arr[@]}"同样是不合法的。
- 在索引数组中,
*(有前置感叹号!):- 在索引数组中,
"${!arr[*]}"是不合法的,因为感叹号用于关联数组来获取所有的键。 - 在关联数组中,
"${!arr[*]}"是错误的写法,正确的应该是"${!arr[@]}",它会展开成数组中的所有键。
- 在索引数组中,
@(有前置感叹号!):- 在索引数组中,
"${!arr[@]}"和"${!arr[*]}"都是不合法的,因为感叹号与@或*结合时仅用于关联数组。 - 在关联数组中,
"${!arr[@]}"会展开成数组中的所有键。
- 在索引数组中,
所以,当遍历关联数组时,应该使用 "${!arr[@]}" 来获取所有的键。
相关文章:

shell编程:求稀疏数组中元素的和(下标不连续)
#!/bin/basharr([2]3 [5]2 [6]2 [9]1)for i in "${!arr[]}" dosum$((sumarr[i])) doneecho $sumBash 脚本中,* 和 符号在数组上下文中有不同的用途。当使用它们来遍历数组时,必须了解它们之间的区别。 * (无前置感叹号 !): 在索引…...

Rust 学习笔记 - 详解数据类型
前言 任何一门编程语言几乎都脱离不了:变量、基本类型、函数、注释、循环、条件判断,这是一门编程语言的语法基础,只有当掌握这些基础语法及概念才能更好的学习 Rust。 标量类型(Scalar Types) 在 Rust 中ÿ…...

构建本地yum源
下载repo数据文件 根据需要修改下载路径和reposync参数 #!/bin/bashlocal_path/repo/remote/rhel9 enabled_repos$(yum repolist enabled | awk NR>3{print $1}) tempfile$(mktemp -t reposync.XXXX)check() {echo "目标目录剩余空间: $(df -h ${local_path} | awk …...
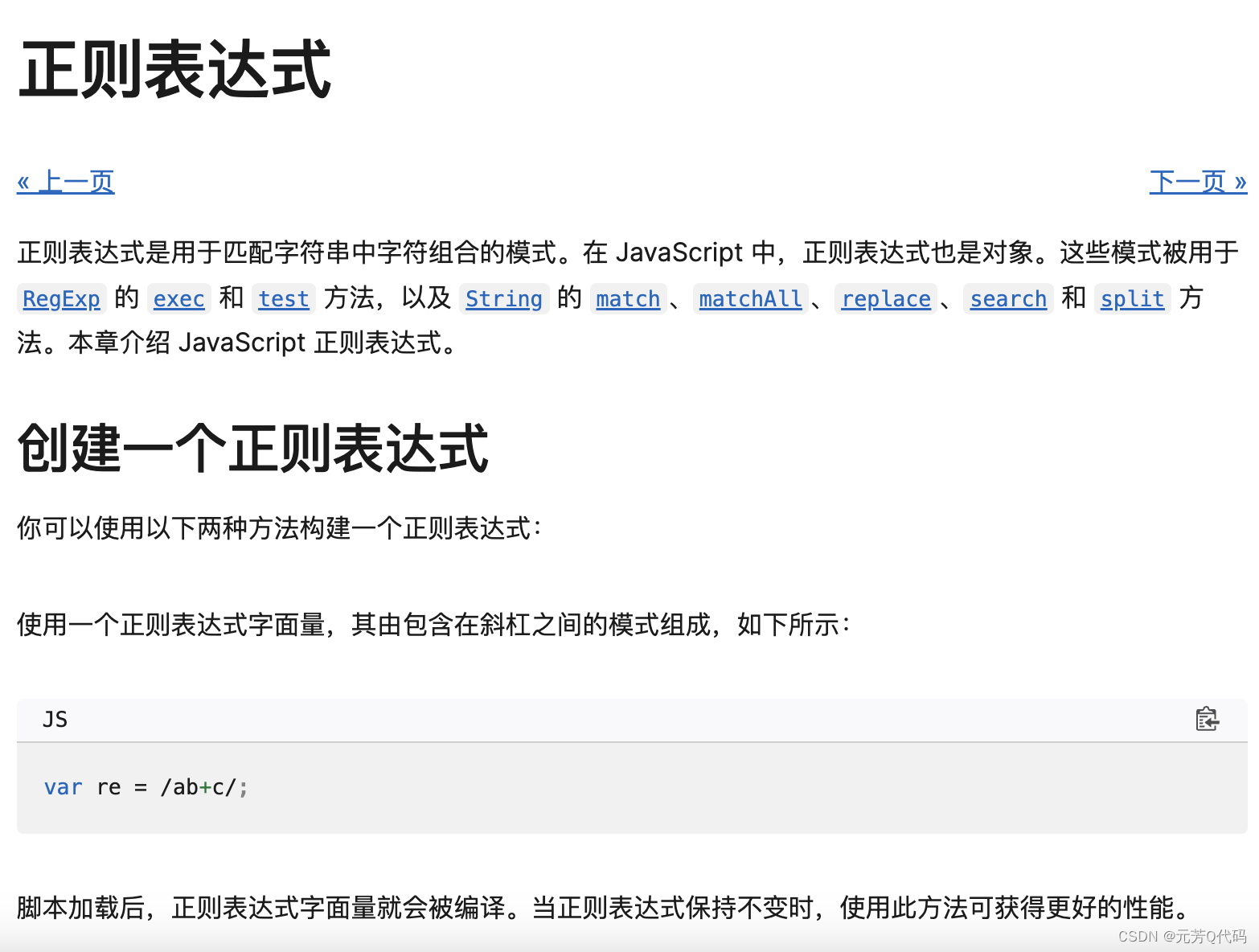
常用的正则表达式,收藏必备!!!
正则表达式是一种强大的文本模式匹配工具,用于在字符串中查找、替换和验证特定模式的文本。下面是一些常用的正则表达式示例: 匹配Email地址: ^[a-zA-Z0-9._%-][a-zA-Z0-9.-]\.[a-zA-Z]{2,}$匹配URL: ^(https?|ftp)://[^\s/$.?#…...

js---webAPI
01 声明变量 js组成: DOM:操作网页内容的,开发页面内容特效和实现用户交互 BOM: DOM树:将 HTML 文档以树状结构直观的表现出来,我们称之为文档树或 DOM 树 文档树直观的体现了标签与标签之间的关系 CSS获取元素的方法 document.querySele…...

git的常用命令有哪些?
Git 是一个流行的分布式版本控制系统,用于跟踪文件的变化、协作开发和管理代码。以下是一些常用的 Git 命令: 创建和克隆仓库: git init:在当前目录初始化一个新的 Git 仓库。git clone <仓库URL>:克隆一个远程仓…...
《动手学深度学习(PyTorch版)》笔记8.5
注:书中对代码的讲解并不详细,本文对很多细节做了详细注释。另外,书上的源代码是在Jupyter Notebook上运行的,较为分散,本文将代码集中起来,并加以完善,全部用vscode在python 3.9.18下测试通过&…...
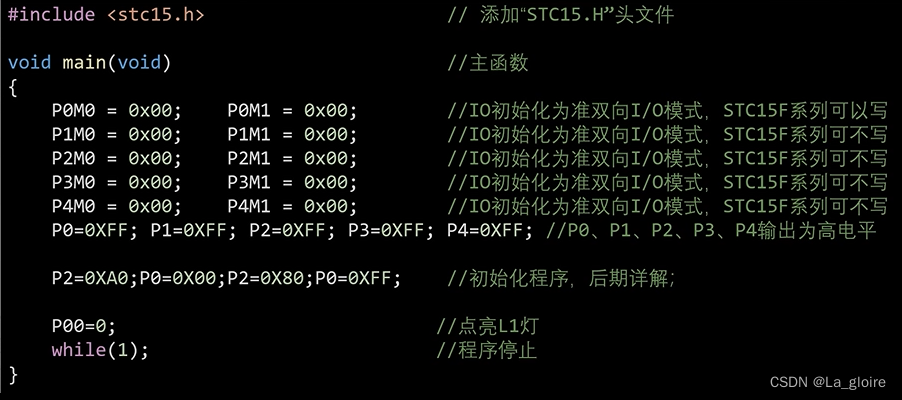
【蓝桥杯单片机入门记录】LED灯(附多个例程)
目录 一、LED灯概述 1.1 LED发光原理 1.2电路原理图 1.3电路实物图 1.4 开发板LED灯原理图 1.4.1共阳极LED灯操控原理(本开发板) (非实际原理图,便于理解版本)由图可以看出,每个LED灯的左边…...

c语言简单json库
文章目录 写在前面头文件源代码使用示例 写在前面 用c语言实现的一个简单json库,极其轻量 仅1个四百多行源码的源文件,和1个头文件 支持对象、数组、数值、字符串类型 github仓库 头文件 对主要的json API的声明 #ifndef ARCOJSON_ARCOJSON_H #defin…...

Linux操作系统基础(七):Linux常见命令(二)
文章目录 Linux常见命令(二) 一、kill命令 二、ifconfig命令 三、clear命令 四、重启与关机命令 五、which命令 六、hostname命令 七、grep命令 八、|管道 九、useradd命令 十、userdel命令 十一、tar命令 十二、su命令 十三、ps命令 Linu…...

进程状态
广义概念: 从广义上来讲,进程分为新建、运行、阻塞、挂起、退出五个状态,其中新建和退出两个状态可以直接理解字面意思。 运行状态: 这里涉及到运行队列的概念,CPU在读取数据的时候,需要把内存中的进程放入…...
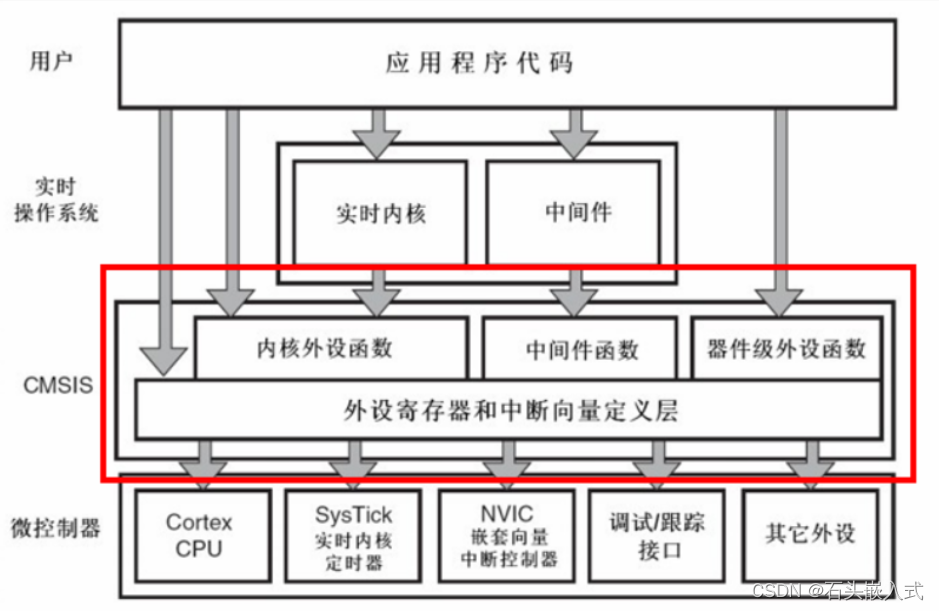
STM32固件库简介与使用指南
1. STM32官方标准固件库简介 STM32官方标准固件库是由STMicroelectronics(ST)提供的一套软件开发工具,旨在简化STM32微控制器的软件开发过程。该固件库提供了丰富的功能和模块,涵盖了STM32微控制器的各种外设,包括但不…...

【开源】SpringBoot框架开发智能教学资源库系统
目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 数据中心模块2.2 课程档案模块2.3 课程资源模块2.4 课程作业模块2.5 课程评价模块 三、系统设计3.1 用例设计3.2 数据库设计3.2.1 课程档案表3.2.2 课程资源表3.2.3 课程作业表3.2.4 课程评价表 四、系统展示五、核心代…...

融资项目——获取树形结构的数据
如下图所示,下列数据是一个树形结构数据,行业中包含若干子节点。表的设计如下图,设置了一个id为1的虚拟根节点。(本树形结构带虚拟根节点共三层) 实现逻辑: 延时展示方法,先展现第二层的信息&a…...

Crypto-RSA2
题目:(BUUCTF在线评测 (buuoj.cn)) 已知e,n,dp/(dq),c求明文: 首先有如下公式: dp ≡ d mod (p-1) ,ed ≡ 1 mod φ(n) ,npq ,φ(n)(p-1)(q-1) python代码实现如下: import libnu…...
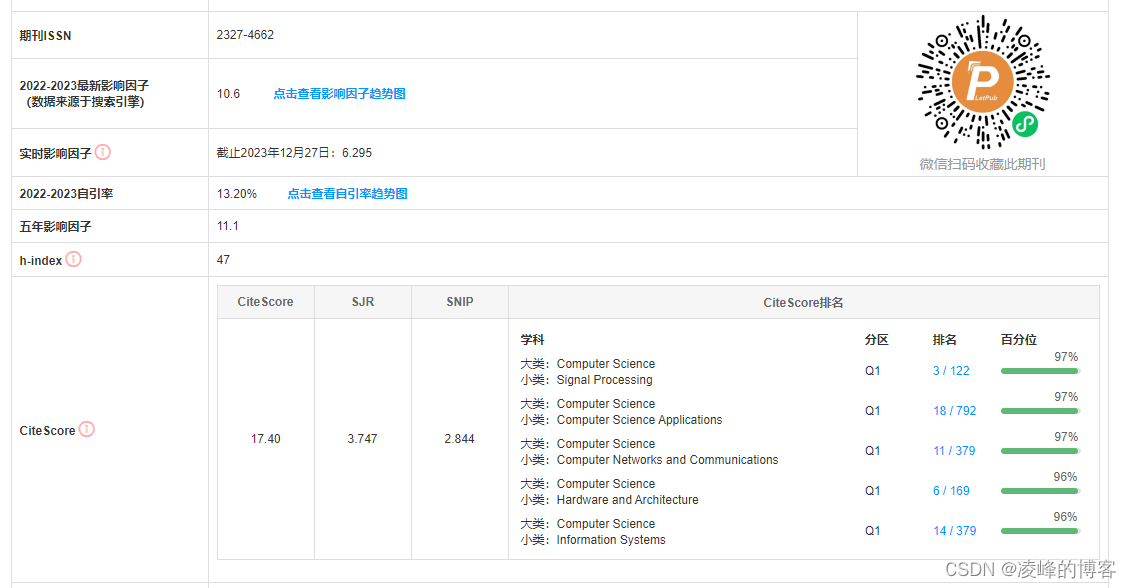
IEEE Internet of Things Journal投稿经验
期刊名:IEEE Internet of Things Journal 期刊分区:中科院一区 Top 影响因子:10.6 投稿状态 (1)2023.11.3,投稿成功,状态为:under review(大u大r)࿱…...
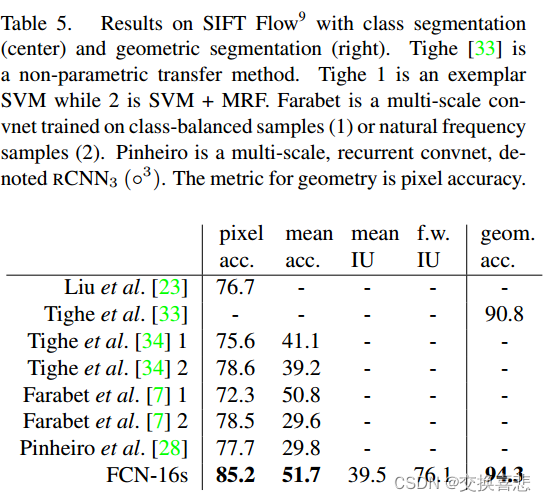
实例分割论文阅读之:FCN:《Fully Convolutional Networks for Semantica Segmentation》
论文地址:https://openaccess.thecvf.com/content_cvpr_2015/papers/Long_Fully_Convolutional_Networks_2015_CVPR_paper.pdf 代码链接:https://github.com/pytorch/vision 摘要 卷积网络是强大的视觉模型,可以产生特征层次结构。我们证明,…...

apk反编译修改教程系列---简单去除apk登陆 修改vip与一些反编译基础常识【十二】
往期教程: 安卓玩机-----反编译apk 修改apk 去广告 去弹窗等操作中的一些常识apk反编译修改教程系列-----修改apk应用名称 任意修改名称 签名【一】 apk反编译修改教程系列-----任意修改apk版本号 版本名 防止自动更新【二】 apk反编译修改教程系列-----修改apk中…...

网络安全习题集
第一章 绪论 4 ISO / OSI 安全体系结构中的对象认证安全服务使用( C ) 机制来完成。 A .访问控制 B .加密 C .数字签名 D .数据完整性 5 身份鉴别是安全服务中的重要一环,以下关于身份鉴别的叙述不正确的是…...

C++中的volatile:穿越编译器的屏障
C中的volatile:穿越编译器的屏障 在C编程中,我们经常会遇到需要与硬件交互或多线程环境下访问共享数据的情况。为了确保程序的正确性和可预测性,C提供了关键字volatile来修饰变量。本文将深入解析C中的volatile关键字,介绍其作用、…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

DeepSeek越强,Kimi越慌?
被DeepSeek吊打的Kimi,还有多少人在用? 去年,月之暗面创始人杨植麟别提有多风光了。90后清华学霸,国产大模型六小虎之一,手握十几亿美金的融资。旗下的AI助手Kimi烧钱如流水,单月光是投流就花费2个亿。 疯…...
