day35|01背包问题、416. 分割等和子集
01背包问题
有n件物品和一个最多能背重量为w的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
例:背包最大重量为4。
物品为:
| 重量 | 价值 | |
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
问背包能背的物品最大价值是多少?
一、二维dp数组01背包
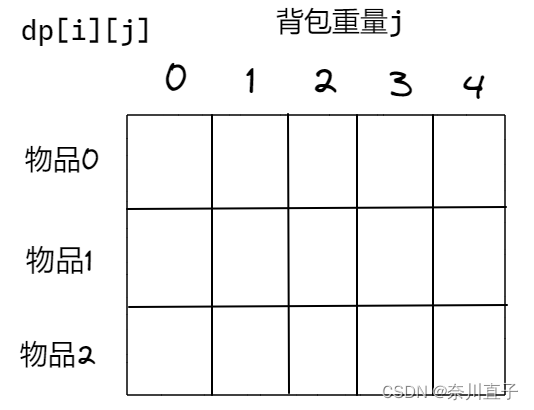
1、确定dp数组以及下标的含义
dp[i][j]:在下标[0,i]的物品任取,放进容量为j的背包,价值总和最大是多少
2、确定递推公式
- 如果背包重量小于物品 i 的重量,那么就不把 i 放进背包里,可得
所以递推公式为:
dp[i][j]=dp[i-1][j]
- 如果背包重量大于物品i的重量,分类讨论:
- 放物品i:dp[i][j]=dp[i-1][j-weight[i]]+value[i]
- 不放物品i:dp[i][j]=dp[i-1][j]
所以递推公式为:
dp[i][j]=Math.max(dp[i-1][j-weight[i]]+value[i],dp[i-1][j])
3、dp数组初始化
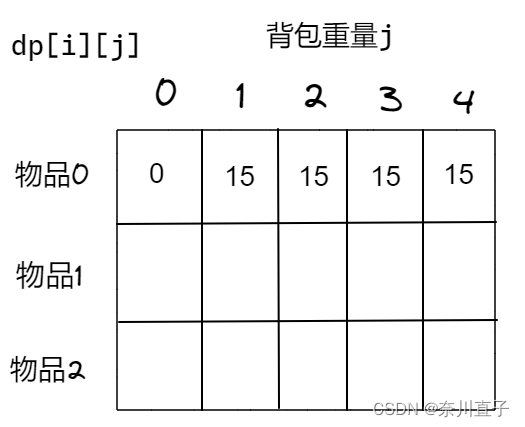
① 根据dp的递推公式dp[i-1][j]可知,i 由i-1推导出来(上面的元素),所以要初始化i=0时的数组元素,即dp[0][j],存放编号为0的物品时,放入各个重量的状态,最大价值总和。
当weight[0]>j 时,dp[0][j]=0。背包容量比编号0的物品重量还小
当weight[0]<=j 时,dp[0][j]=value[0]。背包容量放足够放编号0物品
② 根据dp[i-1][j-weight[i]]+value[i]可知,j 由j-weight[i] 推导出来(左上角的元素),所以要初始化j=0时的元素,即dp[i][0]=0,背包重量为0,放不进去,所以最大价值为0。
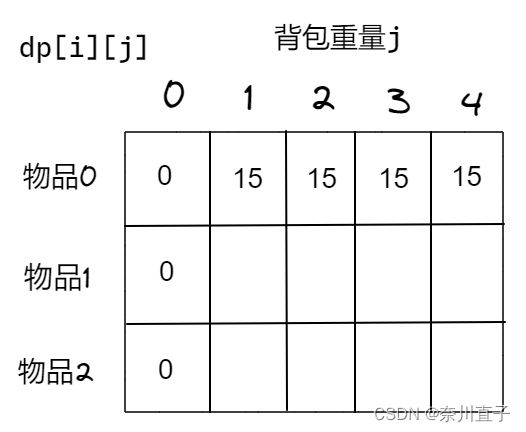
其它元素随意赋初始值,因为会被覆盖。
4、确定遍历顺序
先遍历物品(先横向遍历)或者先遍历重量(先遍历纵向)都可以,都可以保证左上方和上方已有值。
5、举例推导dp数组
public class Main {public static void main(String[] args) {int[] weight = {1,3,4};int[] value = {15,20,30};int bagSize = 4;testWeightBagProblem(weight,value,bagSize);}/*** 动态规划获得结果* @param weight 物品的重量* @param value 物品的价值* @param bagSize 背包的容量*/public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){// 创建dp数组int goods = weight.length; // 获取物品的数量int[][] dp = new int[goods][bagSize + 1];// 初始化dp数组// 创建数组后,其中默认的值就是0//i=0,dp[0][j]for (int j = 0; j <= bagSize; j++) {if (weight[0]>j){dp[0][j]=0;}else if (weight[0]<=j){dp[0][j]=value[0];}}//j=0,dp[i][0]for (int i = 0; i < goods; i++) {dp[i][0] = 0;}// 填充dp数组for (int i = 1; i < weight.length; i++) {for (int j = 1; j <= bagSize; j++) {if (j < weight[i]) {/*** 当前背包的容量都没有当前物品i大的时候,是不放物品i的* 那么前i-1个物品能放下的最大价值就是当前情况的最大价值*/dp[i][j] = dp[i-1][j];} else {/*** 当前背包的容量可以放下物品i* 那么此时分两种情况:* 1、不放物品i* 2、放物品i* 比较这两种情况下,哪种背包中物品的最大价值最大*/dp[i][j] = Math.max(dp[i-1][j] , dp[i-1][j-weight[i]] + value[i]);}}}// 打印dp数组for (int i = 0; i < goods; i++) {for (int j = 0; j <= bagSize; j++) {System.out.print(dp[i][j] + "\t");}System.out.println("\n");}}
}二、一维dp数组01背包(滚动数组)
行覆盖。把dp[i - 1]那一层拷贝到dp[i]上,只用一维数组dp[j]
1、确定dp数组以及下标的含义
dp[j]:容量为j的背包,所背的物品价值可以最大为dp[j]。
2、一维dp数组的递推公式
- 不放物品 i 时,dp[j]=dp[j](相当于dp[i-1][j])
- 放物品 i 时,dp[j]=dp[j-weight[i]]+value[i]
递推公式为:
dp[j]=Math.max(dp[j],dp[j-weight[i]]+value[i])
3、一维dp数组初始化
题目给的价值都是正整数,那么非0下标都初始化为0。dp[j]=0
这样才能让dp数组在递归公式的过程中取的最大的价值,而不是被初始值覆盖了。
4、一维dp数组遍历顺序
① 倒序,背包从大到小,为了保证物品i只被放入一次。
例:物品0的重量weight[0] = 1,价值value[0] = 15
如果正序遍历,假设i=0时
dp[1] = dp[1 - weight[0]] + value[0] = 15
dp[2] = dp[2 - weight[0]] + value[0] = 30
此时dp[2]就已经是30了,意味着物品0,被放入了两次,所以不能正序遍历。
倒序就是先算dp[2]
dp[2] = dp[2 - weight[0]] + value[0] = 15 (dp数组已经都初始化为0)
dp[1] = dp[1 - weight[0]] + value[0] = 15
tips:假设目前有背包容量为10,可以装的最大价值, 记为g[10]。即将进来的物品重量为6。价值为9。
如果不装该物品,显然背包容量无变化,这里对应二维数组,其实就是取该格子上方的格子复制下来,就是所说的滚动下来,直接g[10[ = g[10],这两个g[10]要搞清楚,右边的g[10]是上一轮记录的,也就是对应二维数组里上一层的值,而左边是新的g[10],也就是对应二维数组里下一层的值。
如果装该物品,则背包容量= g[10-6] = g[4] + 9 ,也就是 g[10] = g[4] + 6 ,这里的6显然就是新进来的物品的价值,g[10]就是新记录的,对应二维数组里下一层的值,而这里的g[4]是对应二维数组里上一层的值,通俗的来讲:你要找到上一层也就是上一状态下 背包容量为4时的能装的最大价值,用它来更新下一层的这一状态,也就是加入了价值为9的物品的新状态。
这时候如果是正序遍历会怎么样?g[10] = g[4] + 6 ,这个式子里的g[4]就不再是上一层的了,因为你是正序啊,g[4] 比g[10]提前更新,那么此时程序已经没法读取到上一层的g[4]了,新更新的下一层的g[4]覆盖掉了,这里也就是为啥有题解说一件物品被拿了两次的原因。
② 先遍历物品再遍历背包容量
如果顺序反了,dp[j]就会一直为最大值,最终结果为30,30,30,30,30
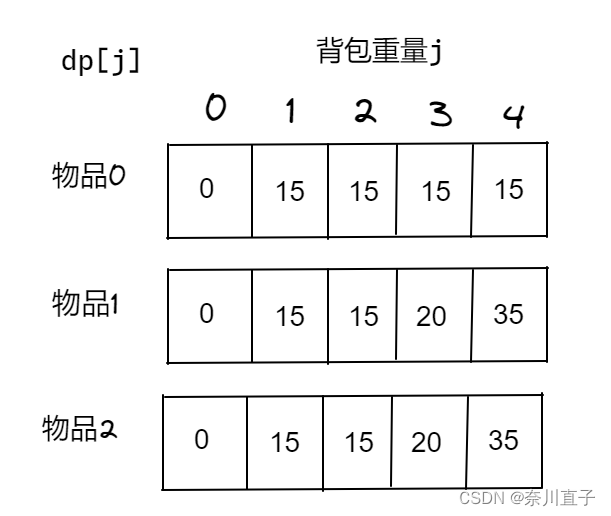
5、举例推导dp数组
一维dp,分别用物品0,物品1,物品2 来遍历背包,最终得到结果如下:
public static void main(String[] args) {int[] weight = {1, 3, 4};int[] value = {15, 20, 30};int bagWight = 4;testWeightBagProblem(weight, value, bagWight);}public static void testWeightBagProblem(int[] weight, int[] value, int bagWeight){int wLen = weight.length;//定义dp数组:dp[j]表示背包容量为j时,能获得的最大价值int[] dp = new int[bagWeight + 1];//遍历顺序:先遍历物品,再遍历背包容量for (int i = 0; i < wLen; i++){for (int j = bagWeight; j >= weight[i]; j--){dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);}}//打印dp数组for (int j = 0; j <= bagWeight; j++){System.out.print(dp[j] + " ");}}416. 分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。
问题分析:
- 背包的体积为sum / 2
- 背包要放入的商品(集合里的元素)重量为 元素的数值,价值也为元素的数值
- 背包如果正好装满,说明找到了总和为 sum / 2 的子集。
- 背包中每一个元素是不可重复放入。
1、确定dp数组以及下标的含义
dp[j]:背包总容量(所能装的总重量)是j,放进物品后,背的最大重量为dp[j]。
2、确定递推公式
01背包的递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
本题,相当于背包里放入数值,那么物品i的重量是nums[i],其价值也是nums[i]。
所以递推公式:dp[j] = max(dp[j], dp[j - nums[i]] + nums[i])
3、dp数组初始化
dp[j]=0,数组初始化自动赋为0
这样才能让dp数组在递推的过程中取得最大的价值,而不是被初始值覆盖了。
4、确定遍历顺序
如同01滚动数组,使用一维dp,物品遍历的for循环放在外层,遍历背包的for循环放在内层,且内层for循环倒序遍历
5、举例推导dp数组
若dp[target]==target,说明可以凑成两个总和相等的数组
class Solution {public boolean canPartition(int[] nums) {int sum=0;for (int i=0;i< nums.length;i++){sum=sum+nums[i];}if (sum%2!=0) return false;//如果不是2的倍数,就不能分成两个相等的数组int target=sum/2;int[] dp=new int[target+1];for(int i=0;i< nums.length;i++){for (int j=target;j>=nums[i];j--){dp[j]=Math.max(dp[j],dp[j-nums[i]]+nums[i]);}}return dp[target]==target;//背包的容量和背包的价值都是nums[i]}
}相关文章:

day35|01背包问题、416. 分割等和子集
01背包问题 有n件物品和一个最多能背重量为w的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。 例:背包最大重量为4。 物品为: 重量价值物品0115物品…...
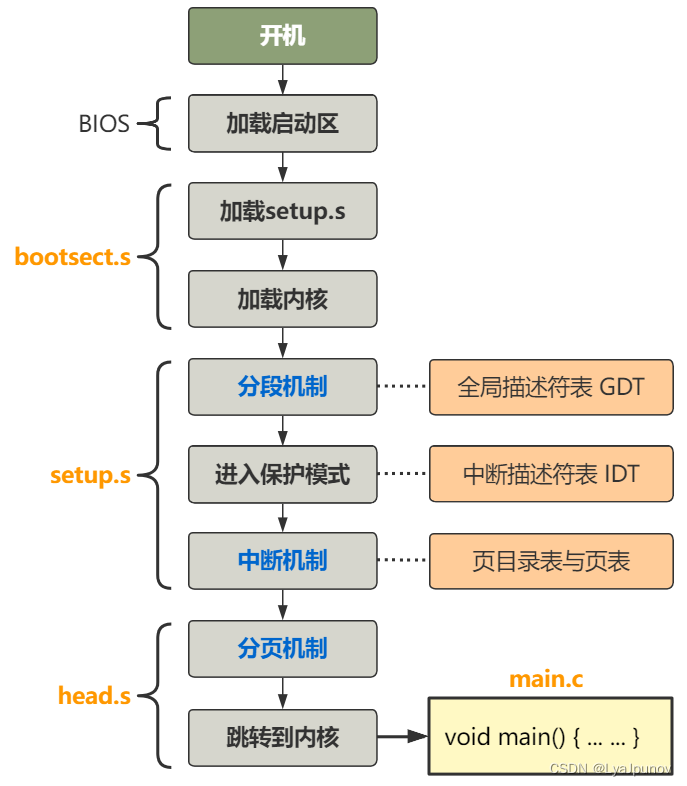
Linux内核启动(3,0.11版本)内核启动完成与进入内核main函数
这一部分是在讲解head.s代码,这个代码与bootsect.s和setup.s在同一目录下,但是head.s程序在被编译生成目标文件后会与内核其他程序一起被链接成system模块,位于system模块的最前面开始部分。system模块将被放置在磁盘上setup模块之后开始的扇…...

【2023】Prometheus-Alertmanager高可用集群
本次实验准备了三个节点,分别为laert-01~03 目录1.安装Alertmanager2.配置启动文件3.验证集群4.关于集群的配置项1.安装Alertmanager 这部分内容在三个节点上都要执行 下载安装包,将安装包解压至/data目录下 wget https://github.com/prometheus/aler…...

2023-2-11 刷题情况
最短路计数 题目描述 给出一个 NNN 个顶点 MMM 条边的无向无权图,顶点编号为 1∼N1\sim N1∼N。问从顶点 111 开始,到其他每个点的最短路有几条。 输入格式 第一行包含 222 个正整数 N,MN,MN,M,为图的顶点数与边数。 接下来 MMM 行&…...

2019_41 考研408
2019年(单链表)41.(13分)设线性表采用带头结点的单链表保存,链表中的结点定义如下:typedef struct node {int data;struct node* next;}NODE;请设计一个空间复杂度为O(1)且时间上尽可能高效的算法,重新排列L中的各结点,得到线性表L(q,a,,a,an…...

Linux账号与用户组
目录 用户标识符:UID与GID 用户账号 /etc/passwd文件结构 1、账号名称 2、密码 3、UID 4、GID 5、用户信息说明栏 6、家目录 7、shell /etc/shadow文件结构 1、账号名称 2、密码 3、最近修改密码的日期 4、密码不可被修改的天数(与第三字…...
有趣的Hack-A-Sat黑掉卫星挑战赛——定位卫星Jackson
国家太空安全是国家安全在空间领域的表现。随着太空技术在政治、经济、军事、文化等各个领域的应用不断增加,太空已经成为国家赖以生存与发展的命脉之一,凝聚着巨大的国家利益,太空安全的重要性日益凸显[1]。而在信息化时代,太空安…...

JAVA集合专题3 —— vector + LinkedList + Set
目录vector的特点LinkedList底层结构模拟双向链表比较ArrayList和LinkedListSet接口基本介绍Set接口的遍历方式Set接口实现类对象的特点Set接口实现类HashSet模拟HashSet/HashMap的底层结构vector的特点 Vector底层是一个对象数组Vector是线程同步的,即线程安全的&…...

Scout:一款功能强大的轻量级URL模糊测试与爬取工具
关于Scout Scout是一款功能强大的轻量级URL模糊测试与爬取工具,可以帮助广大研究人员进行URL模糊测试,并爬取目标Web服务器中难以扫描发现的VHSOT、文件和目录等资源。 项目中包含了一个完整的字典文件,并尽可能地提供了更多的便携性&#…...

leaflet 解决marker呈现灰色边框的问题
第052个 点击查看专栏目录 本示例的目的是介绍演示如何在vue+leaflet示例中处理marker外面有灰色边框的问题,请看未处理会后的图片。 处理后的结果非常满意,不再显示灰色边框。处理方法参考源代码。 直接复制下面的 vue+openlayers源代码,操作2分钟即可运行实现效果; 注意…...

MySQL JSON类型字段的查找与更新
MySQL 提供了丰富的函数用于 JSON 类型字段的查找与更新,详见官方文档。 创建一个表 t1,basic_info 字段为JSON类型: CREATE TABLE t1 (id int(11) NOT NULL AUTO_INCREMENT,basic_info json DEFAULT NULL,PRIMARY KEY (id) ) ENGINEInnoDB DEFAULT CH…...

element Ui树状图控件 spring boot Vue 实现角色授权功能
目录 前言: 二. element ui 2.1官网提供的核心代码 三.表结构 编辑 四.后端 4.1功能分析 4.2实体类 4.3 查询全部权限显示的结果 4.2修改角色权限的后台方法 五.vue 5.0代码总览 5.1树形图 5.2所需要的绑定数据 5.3所需方法 前言: 先上图…...

已解决sc delete MongoDB卸载MongoDB拒绝访问。
已解决sc delete MongoDB卸载MongoDB拒绝访问。 文章目录报错问题报错翻译报错原因解决方法联系博主免费帮忙解决报错报错问题 粉丝群里面的一个小伙伴遇到问题跑来私信我,想卸载MongoDB数据库,但是发生了报错(当时他心里瞬间凉了一大截&…...

python的opencv操作记录11——阈值分割
文章目录传统图像处理分割阈值分割一个应用场景opencv库中的阈值分割固定阈值THRESH_OTSU 大津法阈值自适应阈值传统图像处理分割 现在提到图像分割,很多人会直接想到当前火爆的深度学习的各种分割网络,比如实例分割,语义分割等。其实在传统…...
Python-项目实战--飞机大战-英雄登场(7)
目标设计英雄和子弹类使用pygame.key.get_pressed()移动英雄发射子弹1.设计英雄和子弹类1.1英雄需求游戏启动后,英雄出现在屏幕的水平中间位置,距离屏幕底部120像素英雄每隔0.5秒发射一次子弹,每次连发三枚子弹英雄默认不会移动,需…...
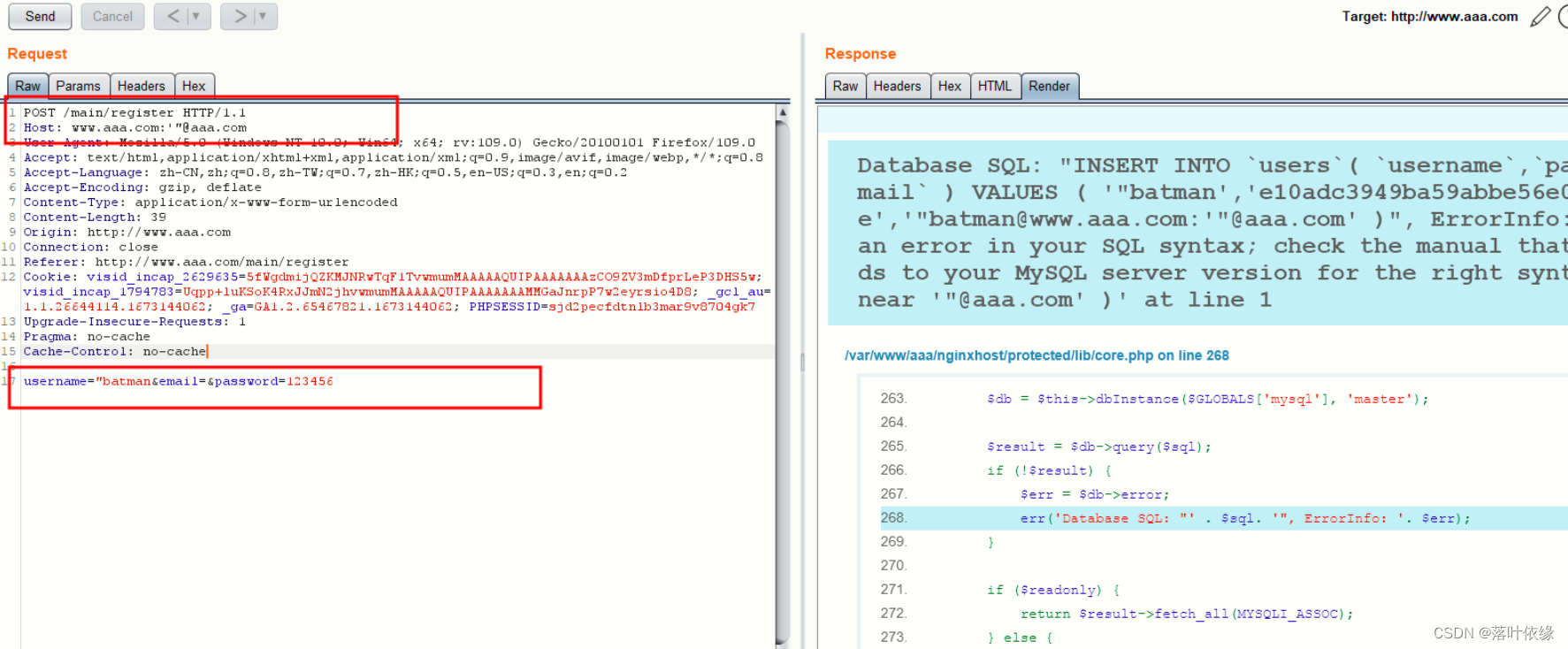
寒假安全作业nginx-host绕过实例复现
1.测试环境搭建 LNMP架构的话,肯定就是linux、nginx、mysql、php四大组件。在后面的复现中我们还会用到https的一部分知识,故这里的nginx就需要使用虚拟主机并且配置https证书,且具有php解析功能。 1.1 基础nginx配置 #1.创建web目录 mkdir …...
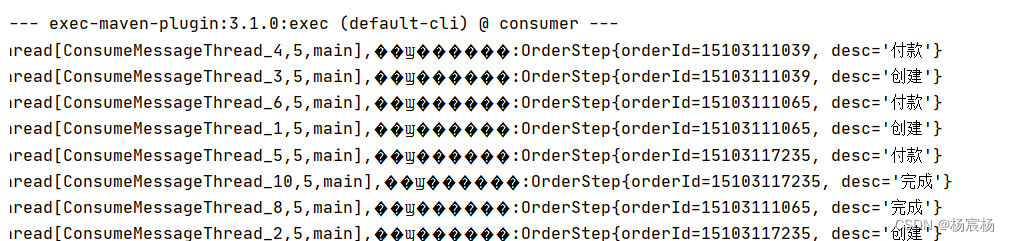
RocketMQ-消息消费模式 顺序消费
RocketMQ-消息消费模式 顺序消费RocketMQ-消息消费模式集群模式集群模式的演示(本身就默认)Rocketmq存储队列广播模式顺序消费如何改实现顺序消费RocketMQ-消息消费模式 集群模式 在消费模式为集群的情况下,如果机器是集群的,消息只会给集群中的其中一台机器消费到 集群模…...
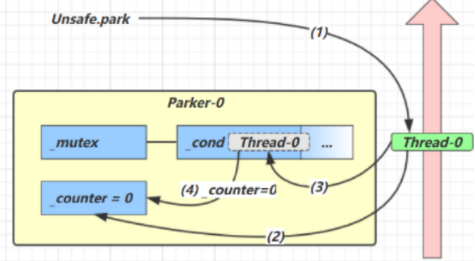
一、Java并发编程之线程、synchronized
黑马课程 文章目录1. Java线程1.1 创建和运行线程方法一:Thread方法二:Runnable(推荐)lambda精简Thread和runnable原理方法三:FutureTask配合Thread1.2 查看进程和线程的方法1.3 线程运行原理栈与栈帧线程上下文切换1.…...
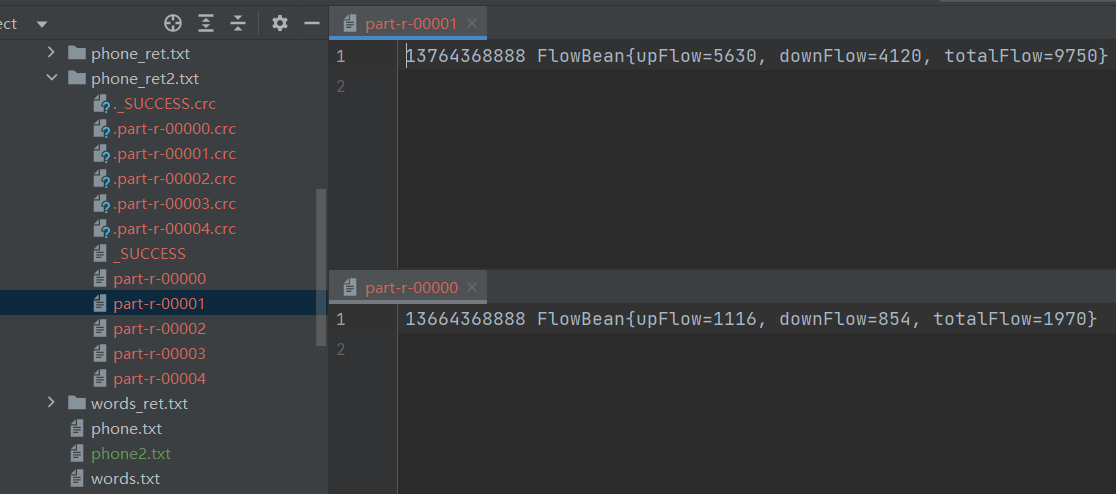
12.hadoop系列之MapReduce分区实践
本文我们学习MapReduce默认分区以及自定义分区实践 当我们要求将统计结果按照条件输出到不同文件(分区),比如按照统计结果将手机归属地不同省份输出到不同文件中(分区) 1.默认Partitioner分区 public class HashPartitioner<K, V> extends Partitioner<…...
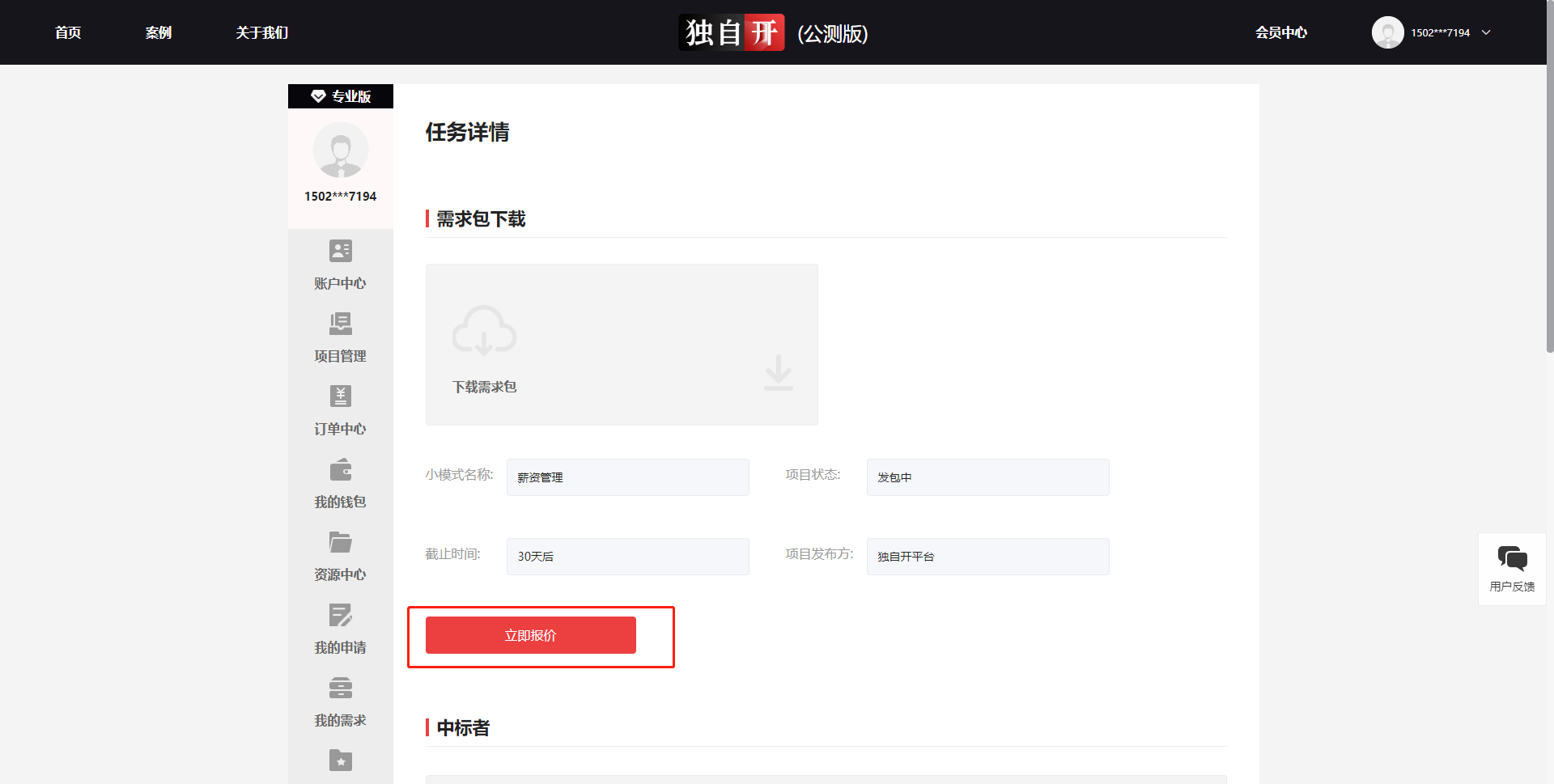
有了独自开,一个人就是一个团队
文章目录 简单介绍优点 优秀案例平台福利总结 简单介绍 独自开是一个基于商品与服务交易全流程的PaaS开发平台。对于开发者,独自开可以协助开发者一个人独自开发一套系统。 优点 独自开有独创的分层标准化平台架构,可以满足系统的任何个性化需求。 …...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...
