奇异值分解(SVD)的应用——图像压缩
SVD方法是模型降阶的一类重要方法,本征正交分解(POD)和平衡截断(BT)都属于SVD类方法。
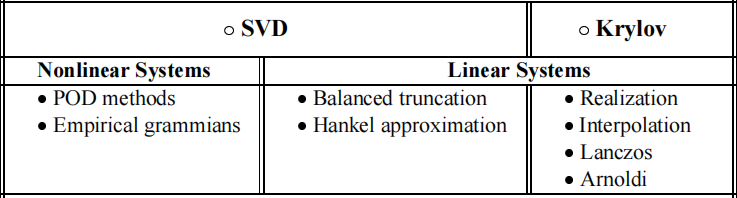
要想深入了解模型降阶技术,我们可以先从SVD的应用入手,做一个直观的了解。
1. SVD的定义和分类




我们想寻找一个A的逼近:Ak,使得rank(Ak) = k < n,且|A - Ak|最小。
下面的定理(也称为Schmidt-Mirsky, Eckart-Young定理)说明矩阵A的低秩逼近可以用SVD实现:

2. SVD在图像压缩中的应用
原始图片, rank=720:

绘制其R,G,B的奇异值:
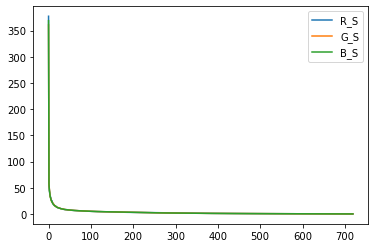
压缩图片,rank=144:

压缩图片,rank=72:

代码:
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.image as imageA = image.imread("svd-image-compression-img.jpg")# Each pixel (typically) consists of 3 bytes — for the red, green and blue components of the color, respectively.
# So, if we want to efficiently store the image, we need to somehow efficiently encode 3 matrices R, G and B
# for each color component, respectively.
# We can extract the 3 color component matrices as briefly mentioned above as follows:
# 0xff代表十进制数值255
R = A[:,:,0] / 0xff
G = A[:,:,1] / 0xff
B = A[:,:,2] / 0xff# Now, we compute the SVD decomposition:
R_U, R_S, R_VT = np.linalg.svd(R)
G_U, G_S, G_VT = np.linalg.svd(G)
B_U, B_S, B_VT = np.linalg.svd(B)# polt the singular values
xaxis = np.arange(0, len(R_S))
plt.plot(xaxis, R_S, label='R_S')
plt.plot(xaxis, G_S, label='G_S')
plt.plot(xaxis, B_S, label='B_S')
plt.legend()relative_rank = 0.1
max_rank = int(relative_rank * min(R.shape[0], R.shape[1]))
print("max rank = %d" % max_rank) # 144def read_as_compressed(U, S, VT, k):Ak = np.zeros((U.shape[0], VT.shape[1]))for i in range(k):U_i = U[:,[i]]VT_i = np.array([VT[i]])Ak += S[i] * (U_i @ VT_i)return Ak## Actually, it is easier and more efficient to perform the same operation
## with a lower-rank matrix multiplication.
# def read_as_compressed(U, S, VT, k):
# return (U[:,:k] @ np.diag(S[:k])) @ VT[:k]R_compressed = read_as_compressed(R_U, R_S, R_VT, max_rank)
G_compressed = read_as_compressed(G_U, G_S, G_VT, max_rank)
B_compressed = read_as_compressed(B_U, B_S, B_VT, max_rank)compressed_float = np.dstack((R_compressed, G_compressed, B_compressed))
compressed = (np.minimum(compressed_float, 1.0) * 0xff).astype(np.uint8)# Plot
plt.figure()
plt.imshow(A)plt.figure()
plt.imshow(compressed)image.imsave("compressed.jpg", compressed)
参考资料:
相关文章:

奇异值分解(SVD)的应用——图像压缩
SVD方法是模型降阶的一类重要方法,本征正交分解(POD)和平衡截断(BT)都属于SVD类方法。 要想深入了解模型降阶技术,我们可以先从SVD的应用入手,做一个直观的了解。 1. SVD的定义和分类 我们想寻找…...

RTDETR改进系列指南
基于Ultralytics的RT-DETR改进项目.(89.9) 为了感谢各位对RTDETR项目的支持,本项目的赠品是yolov5-PAGCP通道剪枝算法.具体使用教程 自带的一些文件说明 train.py 训练模型的脚本main_profile.py 输出模型和模型每一层的参数,计算量的脚本(rtdetr-l和rtdetr-x因为thop库的问…...

类和结构体的区别
类(class)和结构体(struct)是面向对象编程(Object-Oriented Programming,OOP)中常见的两种数据类型,它们在不同的编程语言中有一些共同之处,但也存在一些区别。以下是它们…...

利用Excel模拟投币试验
文章目录 试验前对Excel要进行的设置试验步骤计算正面频率结果图试验前对Excel要进行的设置 进入Excel依次点击如下选项,最后将分析工具库勾选 #mermaid-svg-bIvrxZGI9buCMW6U {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#m…...

WebService接口测试
WebService的理解 WebService就是Web服务的意思,对应的应用层协议为SOAP(相当于HTTP协议),可理解为远程调用技术。 特点: 客户端发送的请求主体内容(请求报文)的格式为XML格式 接口返回的响…...
语音唤醒——
文章目录 配置主代码 参考文档:https://picovoice.ai/docs/quick-start/porcupine-python/ 配置 pip install pvporcupine主代码 ACCESS_KEY:需要将该参数填入即可 # # Copyright 2018-2023 Picovoice Inc. # # You may not use this file except in …...
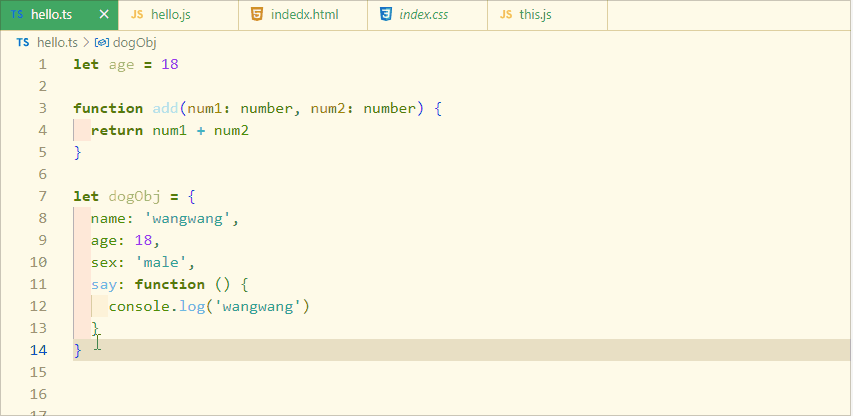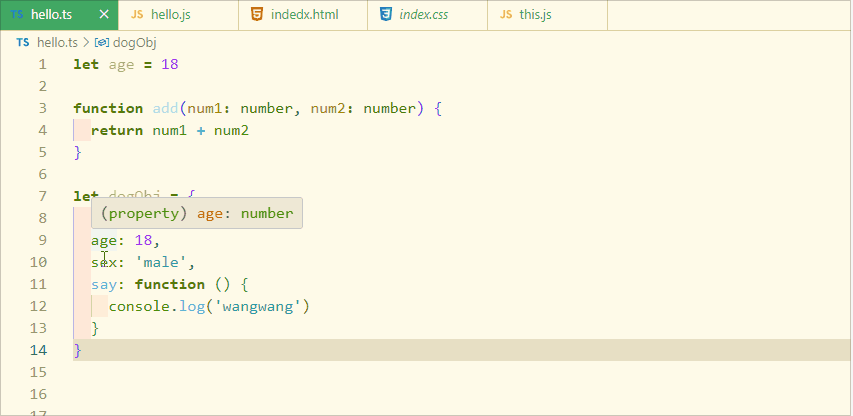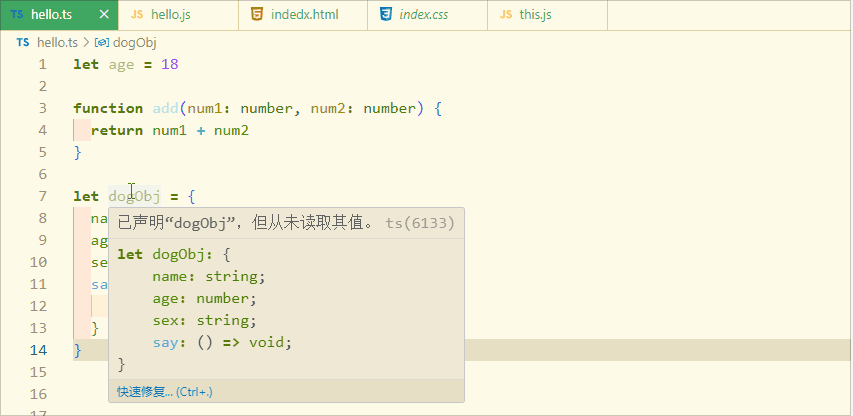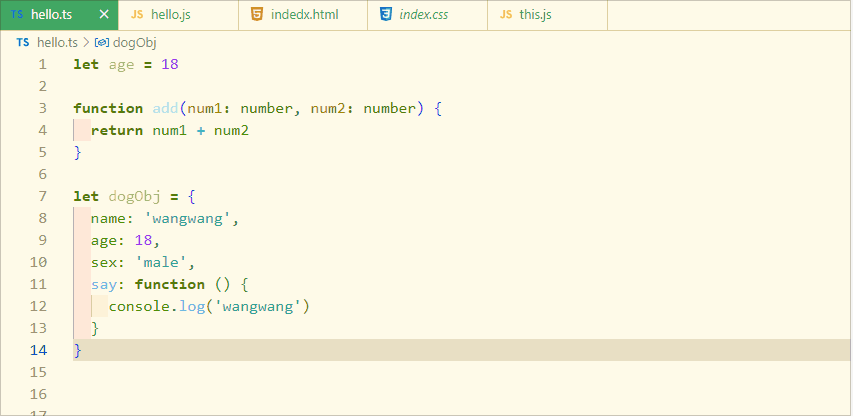
typeScript 类型推论
什么是类型推论? 类型推论是 TypeScript 中的一个特性,它允许开发人员不必显式地指定变量的类型。相反,开发人员可以根据变量的使用情况让 TypeScript 编译器自动推断出类型。例如,如果开发人员将一个字符串赋值给一个变量&#…...

JavaScript 设计模式之代理模式
代理模式 其实这种模式在现在很多地方也都有使用到,如 Vue3 中的数据相应原理就是使用的 es6 中的 Proxy 代理及 Reflect 反射的方式来处理数据响应式 我们日常在使用数据请求时,也会用到一些代理的方式,比如在请求不同的域名,端…...

JavaScript 对象判断
如何判断一个对象是否是Set、Map、Array、Object 参考链接: https://blog.csdn.net/yunchong_zhao/article/details/115915624 let set new Set() let map new Map() let arr [] let obj {}console.log(Object.prototype.toString.call(obj)); // [object Obje…...

Android下SF合成流程重学习之onMessageInvalidate
Android下SF合成流程重学习之onMessageInvalidate 引言 虽然看了很多关于Android Graphics图形栈的文章和博客,但是都没有形成自己的知识点。每次学习了,仅仅是学习了而已,没有形成自己的知识体系,这次趁着有时间,这次…...
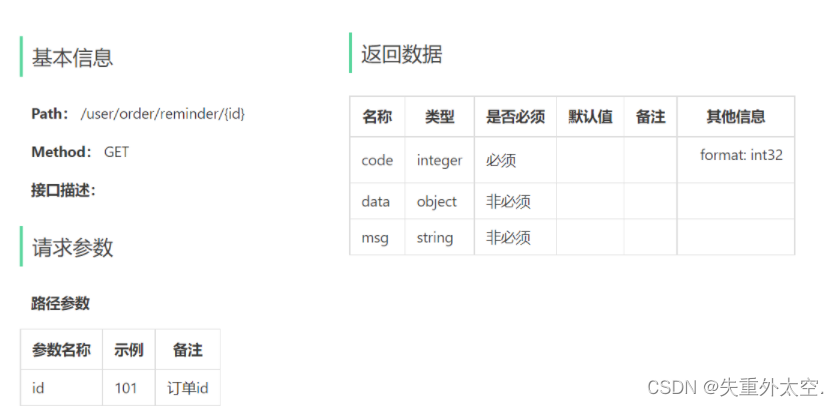
基于SpringBoot+WebSocket+Spring Task的前后端分离外卖项目-订单管理(十七)
订单管理 1. Spring Task1.1 介绍1.2 cron表达式1.3 入门案例1.3.1 Spring Task使用步骤1.3.2 代码开发1.3.3 功能测试 2.订单状态定时处理2.1 需求分析2.2 代码开发2.3 功能测试 3. WebSocket3.1 介绍3.2 入门案例3.2.1 案例分析3.2.2 代码开发3.2.3 功能测试 4. 来单提醒4.1 …...
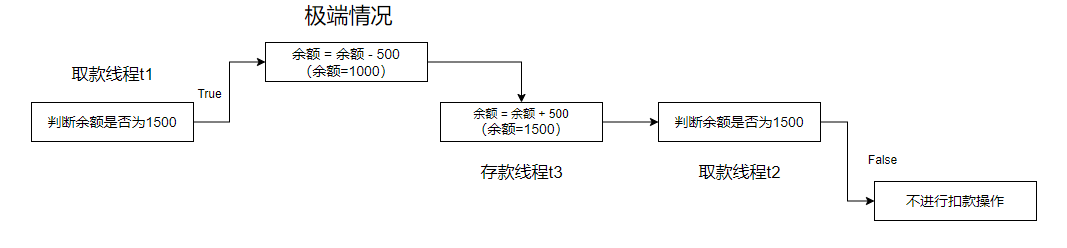
【Java多线程进阶】JUC常见类以及CAS机制
1. Callable的用法 之前已经接触过了Runnable接口,即我们可以使用实现Runnable接口的方式创建一个线程,而Callable也是一个interface,我们也可以用Callable来创建一个线程。 Callable是一个带有泛型的interface实现Callable接口必须重写cal…...

Python算法100例-1.7 最佳存款方案
完整源代码项目地址,关注博主私信’源代码’后可获取 1.问题描述2.问题分析3.算法设计4.完整的程序 1.问题描述 假设银行一年整存零取的月息为0.63%。现在某人手中有一笔钱,他打算在今后5年中的每年年底取出1000元,到第5年时刚…...

ADO世界之FIRST
目录 一、ADO 简介 二、ADO 数据库连接 1.创建一个 DSN-less 数据库连接 2.创建一个 ODBC 数据库连接 3.到 MS Access 数据库的 ODBC 连接 4.ADO 连接对象(ADO Connection Object) 三、ADO Recordset(记录集) 1.创建一个 …...
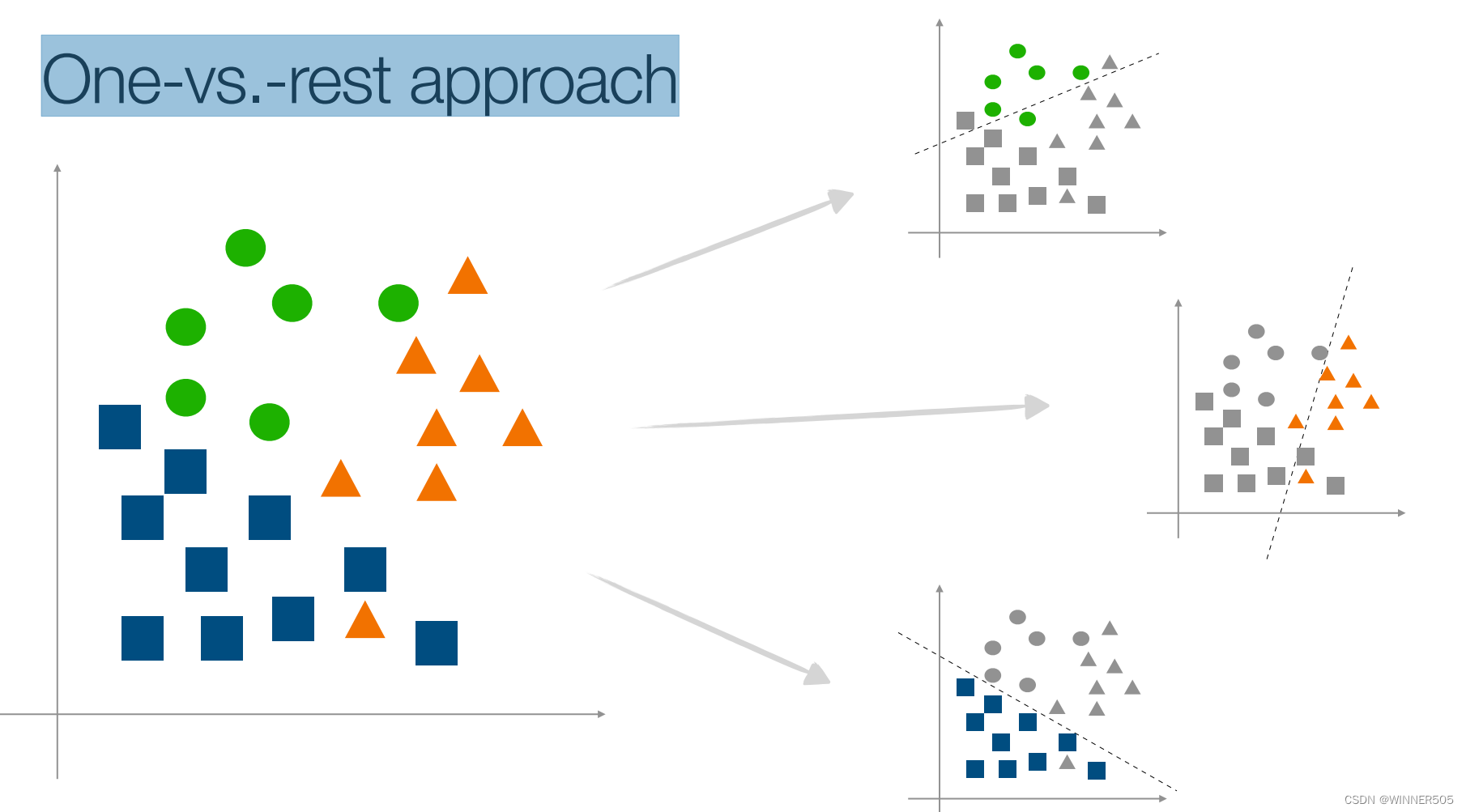
【COMP337 LEC 5-6】
LEC 5 Perceptron : Binary Classification Algorithm 8 感应器是 单个神经元的模型 突触连接的强度取决于接受外部刺激的反应 X input W weights a x1*w1x2*w2....... > / < threshold Bias MaxIter is a hyperparameter 超参数 which has to be chosen…...
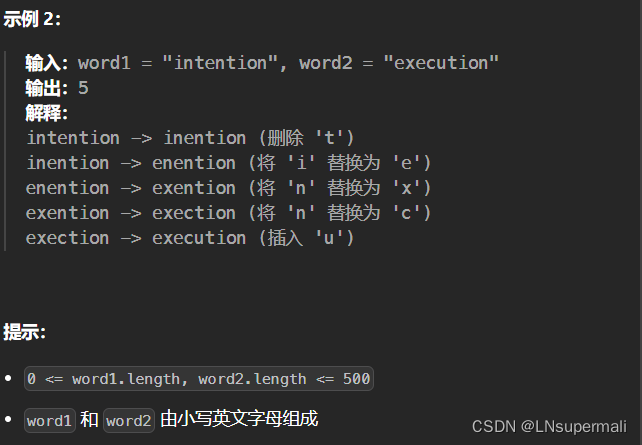
力扣72. 编辑距离(动态规划)
Problem: 72. 编辑距离 文章目录 题目描述思路复杂度Code 题目描述 思路 由于易得将字符串word1向word2转换和word2向word1转换是等效的,则我们假定统一为word1向word2转换!!! 1.确定状态:我们假设现在有下标i&#x…...

linux tree命令找不到:如何使用Linux Tree命令查看文件系统结构
Linux tree命令是一个用于显示文件夹和文件的结构的工具,它可以帮助用户更好地理解文件系统的结构。如果你在linux系统上找不到tree命令,那么可能是因为你的系统中没有安装tree命令。 解决方案 Linux tree命令是一个用于显示文件夹和文件的结构的工具&…...

OJ_最大逆序差
题目 给定一个数组,编写一个算法找出这个数组中最大的逆序差。逆序差就是i<j时,a[j]-a[i]的值 c语言实现 #include <stdio.h> #include <limits.h> // 包含INT_MIN定义 int maxReverseDifference(int arr[], int size) { if (size…...

MyBatis-Plus 实体类里写正则让字段phone限制为手机格式
/* Copyright © 2021User:啾啾修车File:ToupiaoRecord.javaDate:2021/01/12 19:29:12 */ package com.jjsos.repair.toupiao.entity; import com.baomidou.mybatisplus.annotation.IdType; import com.baomidou.mybatisplus.annotation.TableField; import com.baomido…...

K8S之运用污点、容忍度设置Pod的调度约束
污点、容忍度 污点容忍度 taints 是键值数据,用在节点上,定义污点; tolerations 是键值数据,用在pod上,定义容忍度,能容忍哪些污点。 污点 污点是定义在k8s集群的节点上的键值属性数据,可以决…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...
