摆(行列式、杜教筛)
有一个 n × n n\times n n×n 的矩阵 A A A,满足:
A i , j = { 1 i = j 0 i ≠ j ∧ i ∣ j C otherwise A_{i,j}=\begin{cases} 1 &i=j\\ 0 &i\not=j\land i\mid j\\ C &\text{otherwise} \end{cases} Ai,j=⎩ ⎨ ⎧10Ci=ji=j∧i∣jotherwise
求 det ( A ) \det(A) det(A)。答案模 998244353 998244353 998244353。
n ≤ 1 0 11 n\le10^{11} n≤1011。
显然当 C = 0 C=0 C=0 时答案为 1 1 1,当 C = 1 C=1 C=1 时若 n ≤ 2 n\le2 n≤2 则答案为 1 1 1 否则为 0 0 0。
首先 A A A 形如:
[ 1 0 0 0 0 … C 1 C 0 C … C C 1 C C … C C C 1 C … C C C C 1 … ⋮ ⋮ ⋮ ⋮ ⋮ ⋱ ] \begin{bmatrix} 1&0&0&0&0&\dots\\ C&1&C&0&C&\dots\\ C&C&1&C&C&\dots\\ C&C&C&1&C&\dots\\ C&C&C&C&1&\dots\\ \vdots&\vdots&\vdots&\vdots&\vdots&\ddots \end{bmatrix} 1CCCC⋮01CCC⋮0C1CC⋮00C1C⋮0CCC1⋮……………⋱
考虑把主对角线的 1 1 1 换位 C + x C+x C+x,这样 det ( A ) \det(A) det(A) 就可看做关于 x x x 的多项式,求值只需代入 x = 1 − C x=1-C x=1−C 即可。
这里有个式子
det ( A ) = ∑ S ⊂ { 1 , 2 , … , n } det ( B S ) ⋅ x n − ∣ S ∣ \det(A)=\sum\limits_{S\subset\{1,2,\dots,n\}}\det(B_S)\cdot x^{n-|S|} det(A)=S⊂{1,2,…,n}∑det(BS)⋅xn−∣S∣
其中 B S B_S BS 表示把矩阵 A A A 主对角线元素换成 C C C,只选出行列都在 S S S 中的元素拼接形成的矩阵。
例如: B { 1 , 2 , 4 , 5 , 8 } = [ C 0 0 0 0 C C 0 C 0 C C C C 0 C C C C C C C C C C ] B_{\{1,2,4,5,8\}}=\begin{bmatrix} C&0&0&0&0\\ C&C&0&C&0\\ C&C&C&C&0\\ C&C&C&C&C\\ C&C&C&C&C\\ \end{bmatrix} B{1,2,4,5,8}= CCCCC0CCCC00CCC0CCCC000CC
证明考虑感性理解。设 i = n − ∣ S ∣ i=n-|S| i=n−∣S∣,对于 x i x^{i} xi 的系数,考虑行列式的定义,要选出行列都互不相同的 n n n 个数相乘,由于只有主对角线上的 C + x C+x C+x 有次数贡献,于是考虑选出来 m m m 个主对角线上的元素( m ≥ i m\ge i m≥i),剩下的行列拼接在一起后面选。我们此时发现 n − m + m − i = n − i n-m+m-i=n-i n−m+m−i=n−i,说明 B S B_S BS 是由 S S S 的行列与 m m m 行列之中选 m − i m-i m−i 个组成的, ( C + x ) m (C+x)^m (C+x)m 中 x i x^i xi 的系数为 ( m i ) C m − i \binom{m}{i}C^{m-i} (im)Cm−i,恰好满足条件。
我们观察 B S B_S BS,发现如果 S S S 中元素两两整除,那么 B S B_S BS 是下三角矩阵, det ( B S ) = C ∣ S ∣ \det(B_S)=C^{|S|} det(BS)=C∣S∣。否则可以证明 det ( B S ) = 0 \det(B_S)=0 det(BS)=0。
考虑归纳法证明,如果 S S S 中存在两个数不为 S S S 中其他任何数的因子,那么矩阵中就会出现两行 C C C, det ( B S ) = 0 \det(B_S)=0 det(BS)=0;否则 S S S 中最大的数一定是其他数的倍数,从而只有最后一行全为 C C C,不妨删去最后一行列。这样递归下去,容易发现结论成立。
设 r = C 1 − C r=\frac{C}{1-C} r=1−CC,于是 det ( A ) = ( 1 − C ) n ∑ S 中元素两两整除 r ∣ S ∣ \det(A)=(1-C)^n\sum\limits_{S中元素两两整除} r^{|S|} det(A)=(1−C)nS中元素两两整除∑r∣S∣
令 f i f_i fi 表示所有满足 S S S 中最大元素为 i i i 的 r ∣ S ∣ r^{|S|} r∣S∣ 之和(特别地, f 1 = 1 + r f_1=1+r f1=1+r)。容易得到转移式子
f i = r ∑ j ∣ i , j < i f j f_i=r\sum\limits_{j\mid i,j<i}f_j fi=rj∣i,j<i∑fj
令 s ( i ) = ∑ j = 1 i f j s(i)=\sum\limits_{j=1}^if_j s(i)=j=1∑ifj,我们要求出 s ( n ) s(n) s(n)。
考虑杜教筛,我们构造 g ( n ) = { − 1 n = 1 r n > 1 g(n)=\begin{cases}-1&n=1\\r&n>1\end{cases} g(n)={−1rn=1n>1,函数 h = f ∗ g h=f*g h=f∗g,容易验证 h ( n ) = { − r − 1 n = 1 0 n > 1 h(n)=\begin{cases}-r-1&n=1\\0&n>1\end{cases} h(n)={−r−10n=1n>1。套用公式 g ( 1 ) s ( n ) = ∑ i = 1 n h i − ∑ i = 2 n g ( i ) s ( ⌊ n i ⌋ ) g(1)s(n)=\sum\limits_{i=1}^nh_i-\sum\limits_{i=2}^ng(i)s(\lfloor\frac ni\rfloor) g(1)s(n)=i=1∑nhi−i=2∑ng(i)s(⌊in⌋),可以得到 s ( n ) s(n) s(n) 的转移式子
s ( n ) = 1 + r + r ∑ i = 2 n s ( ⌊ n i ⌋ ) s(n)=1+r+r\sum\limits_{i=2}^ns(\lfloor\frac ni\rfloor) s(n)=1+r+ri=2∑ns(⌊in⌋)
到此直接按式子求答案是 O ( n 3 4 ) O(n^{\frac34}) O(n43) 的,如果预处理出前 n 2 3 n^{\frac23} n32 个 s ( n ) s(n) s(n),求值可以做到 O ( n 2 3 ) O(n^{\frac23}) O(n32)。
但是预处理时间复杂度容易带上 log \log log,所以要考虑优化。
设 n = ∏ p i k i n=\prod p_i^{k_i} n=∏piki,如果我们把 p 1 , p 2 , … p_1,p_2,\dots p1,p2,… 依次换成 2 , 3 , 5 , 7 , … 2,3,5,7,\dots 2,3,5,7,…,所得到的数设为 n ′ n' n′,容易发现 f n = f n ′ f_n=f_{n'} fn=fn′。这启发我们 f n f_n fn 的值只与可重集 k k k 有关。通过暴力发现可重集的数量很少,于是我们可以暴力求出这些“代表”的函数值,然后让找到其他数所对应的“代表”。用欧拉筛实现,具体实现可参照代码。
总的时间复杂度为 O ( n 2 3 ) O(n^{\frac23}) O(n32)。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll mod=998244353,N=2e7+1;
ll n,c,R;
int a[N],p[N],cnt,m,to[N],num[N],Max[N];
ll S[N];
unordered_map<ll,int> ma;
ll ksm(ll a,ll b)
{ll ans=1;while(b){if(b&1) ans=ans*a%mod;b>>=1;a=a*a%mod;}return ans;
}
ll s(ll n)
{if(n<=m) return S[n];if(ma.count(n)) return ma[n];ll ans=1+R;for(ll i=2,r;i<=n;i=r+1){r=n/(n/i);ans=(ans+(r-i+1)%mod*R%mod*s(n/i))%mod;}return ma[n]=ans;
}
void init(int n)
{a[1]=1,to[1]=S[1]=1+R;for(int i=2;i<=n;i++){if(!a[i]){p[++cnt]=i;to[i]=2;num[i]=1;Max[i]=i;}if(to[i]==i){for(int j=1;j*j<=i;j++) if(i%j==0) S[i]=(S[i]+S[j]+(j*j<i&&j>1)*S[i/j])%mod;S[i]=S[i]*R%mod;}else S[i]=S[to[i]];for(int j=1;j<=cnt&&i*p[j]<=n;j++){int x=i*p[j];a[x]=1;Max[x]=Max[i];if(i%p[j]==0){num[x]=num[i];to[x]=to[x/Max[x]]*p[num[x]];break;}num[x]=num[i]+1;to[x]=to[x/Max[x]]*p[num[x]];}}for(int i=2;i<=n;i++) S[i]=(S[i]+S[i-1])%mod;
}
int main()
{freopen("bigben.in","r",stdin);freopen("bigben.out","w",stdout);cin>>n>>c;if(!c) cout<<1,exit(0);if(c==1) cout<<(n<=2),exit(0);R=c*ksm(1-c+mod,mod-2)%mod;init(m=min(n,N-1));cout<<s(n)*ksm(1-c+mod,n)%mod;
}
相关文章:
)
摆(行列式、杜教筛)
有一个 n n n\times n nn 的矩阵 A A A,满足: A i , j { 1 i j 0 i ̸ j ∧ i ∣ j C otherwise A_{i,j}\begin{cases} 1 &ij\\ 0 &i\notj\land i\mid j\\ C &\text{otherwise} \end{cases} Ai,j⎩ ⎨ ⎧10Cijij∧i∣jotherwi…...

尝试以语法对照表格形式学习新语言:c,rust
以语法对照表格形式学习新语言,以rust为例。 关于rust的个人看法: 能否替代c?部分场景可以,长远看并不会。如果c再扩一些关键字,类似cpp的吸星大法式扩充,rust并不具备优势。解决了c的内存管理问题&#x…...
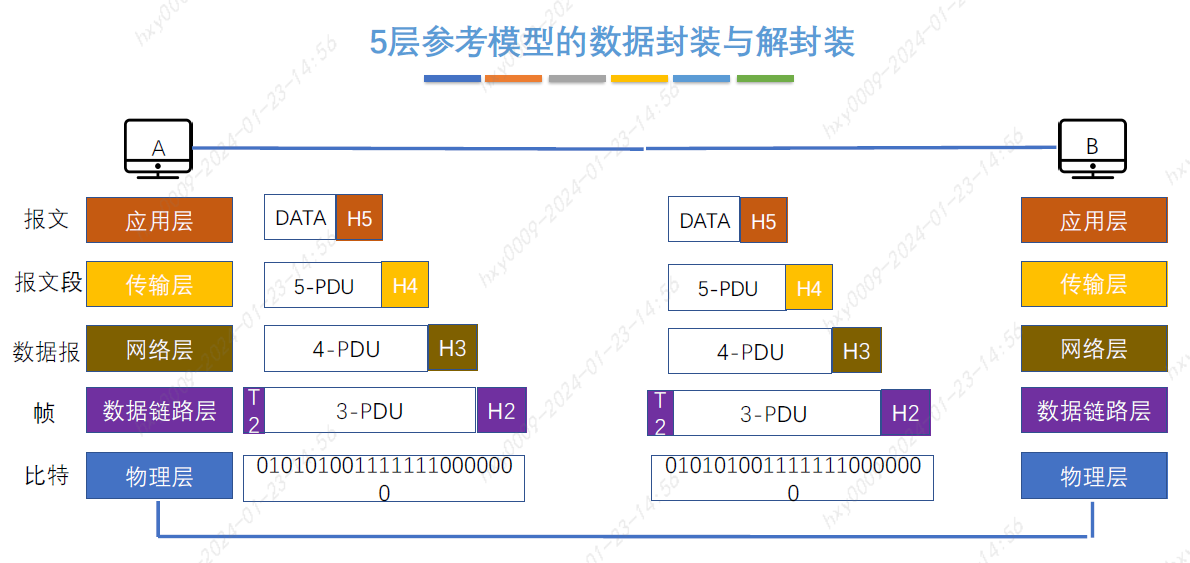
408计算机网络--基础概论
学习计算机网络走以前需要首先明白一个大的概念,计算机网络通常分为通信子网(实现数据通信)和资源子网(实现资源共享/数据处理)七层妖塔 计算机网络:是一个将分散的、具有独立功能的计算机系统࿰…...
数据库应用:kylin 部署 达梦数据库DM8
目录 一、实验 1.环境 2.部署前规划 3.部署达梦数据库DM8 4.创建数据库及数据库事例管理 5.达梦数据库的基本操作 二、问题 1.xhost命令报错 2.执行安装程序DMInstall.bin 报错 3.解压安装程序报错 4.安装程序找不到文件 5.图像化界面打不开 6.安装内存太小 7.打开…...
、sqlx库)
GO框架基础 (二)、sqlx库
在 Go 语言中,sqlx 包是一个用于数据库操作的库,它建立在标准库的 database/sql 包之上,并提供了一些额外的功能,以简化和增强与数据库的交互。sqlx 的目标是通过提供更方便的 API 和一些附加功能来改善在 Go 中进行 SQL 数据库查…...

Expected class selector “.menuChildMall“ to be kebab-case报错原因
 使用stylelint格式化css文件时候报上述错误: 原因: css类名未使用-分隔符 将类名修改为: .menu-child-mall形式即可...
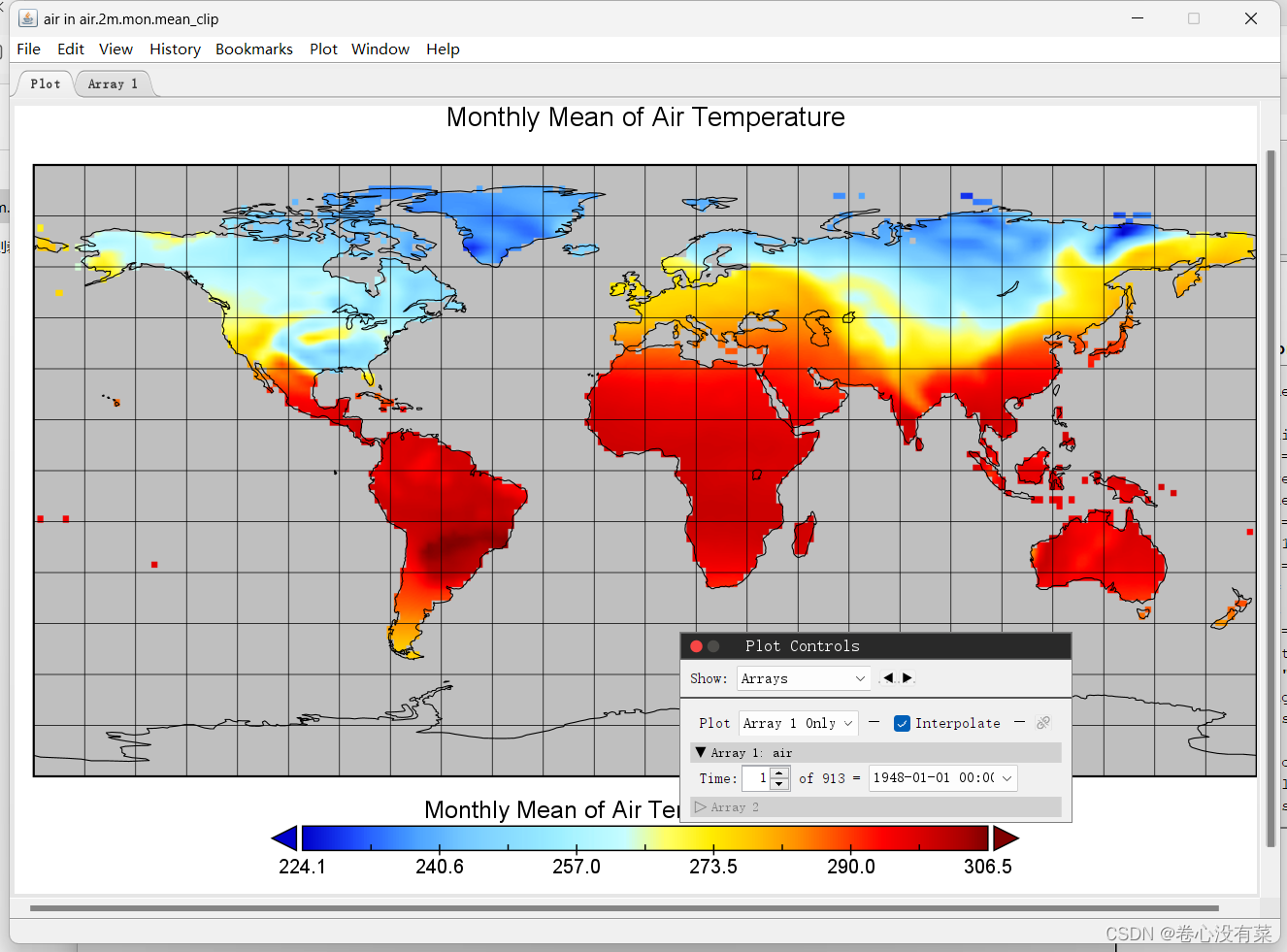
NC文件不规则裁剪(利用shp文件裁剪)(三)
文章目录 前言实例数据代码部分需要的库加载文件写入地理信息裁剪NC结果 完整代码奉上 前言 Hello大家好呀,最近正好需要用到多个SHP去裁剪NC,按照我以前的两种办法(办法1和办法2)操作的话,我自己都会破防,…...
java 宠物在线商城系统Myeclipse开发mysql数据库web结构jsp编程servlet计算机网页项目
一、源码特点 java 宠物在线商城系统是一套完善的java web信息管理系统 servletdaobean mvc模式,对理解JSP java编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S 模式开发。开发环境为TOMCAT7.0,Myeclipse8.5开发&…...

三防平板丨手持工业平板丨ONERugged工业三防平板丨推动数字化转型
随着科技的发展,数字化转型已经成为企业转型升级的必由之路。而在数字化转型中,三防平板作为一种重要的工具,可以极大地推动企业的数字化转型。本文将从以下几个方面探讨三防平板如何推动数字化转型。 一、提高工作效率 ONERugged加固平板的…...

【Linux | C++ 】基于环形队列的多生产者多消费者模型(Linux系统下C++ 代码模拟实现)
阅读导航 引言一、生产者消费者模型二、环形队列简介三、基于环形队列的生产者消费者模型(C 代码模拟实现)⭕Makefile文件⭕ . h 头文件✅sem.hpp✅ringQueue.hpp ⭕ . cpp 文件✅testMain.cpp 温馨提示 引言 在上一篇文章中,我们深入探讨了…...

【Docker】Docker存储卷
文章目录 一、什么是存储卷二、为什么需要存储卷三、存储卷分类四、管理卷Volume创建卷方式一:Volume 命令操作方式二:-v 或者--mount 指定方式三:Dockerfile 匿名卷 操作案例Docker 命令创建管理卷Docker -v 创建管理卷Docker mount 创建管理…...

基于python的租车管理平台/汽车租赁网站
功能介绍 平台采用B/S结构,后端采用主流的Python语言进行开发,前端采用主流的Vue.js进行开发。 整个平台包括前台和后台两个部分。 前台功能包括:首页、详情页、用户中心、家政入驻模块。后台功能包括:总览、车辆管理、分类管理…...

【JVM】双亲委派机制
📝个人主页:五敷有你 🔥系列专栏:JVM ⛺️稳中求进,晒太阳 双亲委派机制 在Java中如何使用代码的方式去主动加载一个类呢? 方式1:使用Class.forName方法,使用当前类的类加载…...

分布式id实战
目录 常用方式 特征 潜在问题 信息安全 高性能 UUID 雪花算法 数据库生成 美团Leaf方案 Leaf-segment 数据库方案 Leaf-snowflake 方案 常用方式 uuid雪花算法数据库主键 特征 全局唯一趋势递增信息安全 潜在问题 信息安全 如果id连续递增, 容易被爬虫, 批量下…...

深入了解 SOCKS5 代理、代理 IP 和 HTTP
在网络通信和数据传输中,代理服务器扮演着至关重要的角色。本文将深入探讨 SOCKS5 代理、代理 IP 和 HTTP,揭示它们的工作原理、应用场景以及优缺点。 1. SOCKS5 代理 SOCKS(Socket Secure)是一种网络协议,允许客户端…...
外包干了3个多月,技术退步明显。。。。
先说一下自己的情况,本科生,19年通过校招进入广州某软件公司,干了接近3年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测试…...

Unity之闪电侠大战蓝毒兽(简陋的战斗系统)
目录 🎨一、创建地形 🎮二、创建角色 🏃2.1 动画 🏃2.2 拖尾 🏃2.3 角色控制 🏃2.4 技能释放 🏃2.5 准星 📱三、创建敌人 🐲3.1 选择模型 🐲3.…...

C# 菜鸟级别有关于redis的使用
public IActionResult Index() { ConnectionMultiplexer _conn ConnectionMultiplexer.Connect("127.0.0.1:6379");//初始化 var database _conn.GetDatabase(7);//指定连接的库 0 RedisHelper redisHelper new Redi…...

AlexNet的出现推动深度学习的巨大发展
尽管AlexNet(2012)的代码只比LeNet(1998)多出几行,但学术界花了很多年才接受深度学习这一概念,并应用其出色的实验结果。 AlexNet(由Alex Krizhevsky、Ilya Sutskever和Geoffrey Hinton共同设计…...

2024面试offer收割宝典字节篇
1.IO 模型有哪些,讲讲你理解的 nio ,他和 bio,aio 的区别是啥, 谈谈 reactor 模型。 IO 模型主要包括以下几种:1. 阻塞 I/O (BIO): 当一个线程调用 read() 或 write() 系统调用时,如果数据没有准备好或者缓冲区已满,则该线程会被操作系统阻塞,直到有数据可读或写入完…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

PydanticAI快速入门示例
参考链接:https://ai.pydantic.dev/#why-use-pydanticai 示例代码 from pydantic_ai import Agent from pydantic_ai.models.openai import OpenAIModel from pydantic_ai.providers.openai import OpenAIProvider# 配置使用阿里云通义千问模型 model OpenAIMode…...
