数据结构与算法:栈
朋友们大家好啊,在链表的讲解过后,我们本节内容来介绍一个特殊的线性表:栈,在讲解后也会以例题来加深对本节内容的理解
栈
- 栈的介绍
- 栈进出栈的变化形式
- 栈的顺序存储结构的有关操作
- 栈的结构定义与初始化
- 压栈操作
- 出栈操作
- 获取栈顶元素和有效元素个数
- 判断是否为空和栈的销毁
- 栈的链式存储结构的有关操作
- 链表的创建
- 链式栈的定义
- 初始化
- 压栈和出栈
- 检查栈是否为空
- 栈的应用--有效的扩号
栈的介绍
在应用软件中,栈的应用非常普遍,比如使用浏览器上网时,会有一个后退键,点击后可以按访问顺序的逆序加载浏览过的网页
很多类似的软件,比如word等文档或编辑软件都有撤销的操作,也是用栈的方式来实现的
栈是一种特殊的线性数据结构,仅支持在一个位置进行添加元素(称为“入栈”或“push”操作)和移除元素(称为“出栈”或“pop”操作)的操作。这个位置就是栈顶(Top)。由于栈是后进先出(LIFO, Last In First Out)的数据结构,最后一个添加到栈中的元素将是第一个被移除。
栈是限定仅在表尾进行插入和删除操作的线性表
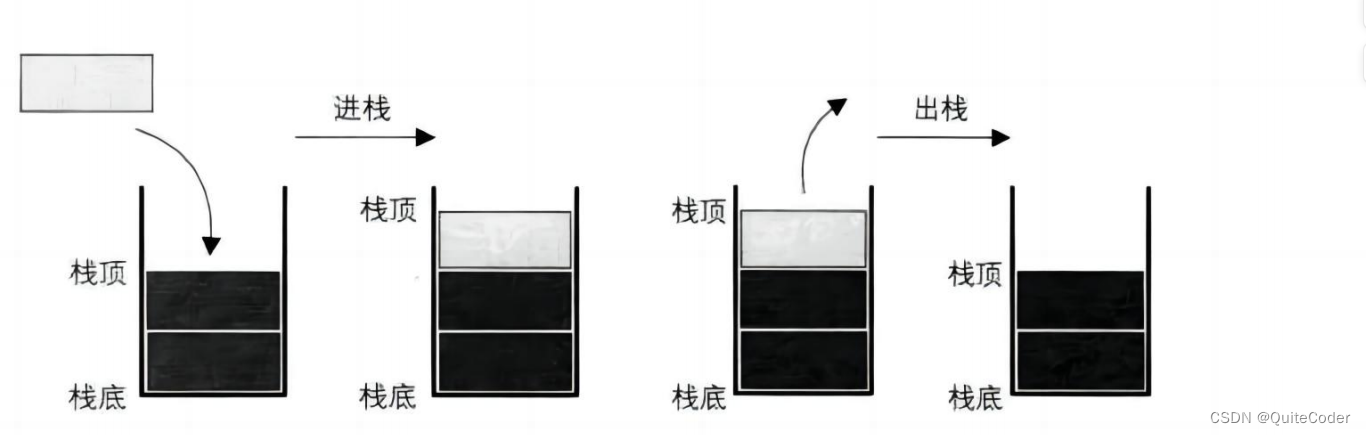
栈首先是一个线性表,说明栈元素具有线性关系,在定义中说在线性表的表尾进行插入和删除操作,这里的表尾是指栈顶
它的特殊之处就在于它的删除和插入始终只能在栈顶进行
栈进出栈的变化形式
首先提一个问题,最先进栈的元素,是不是一定最后出栈呢?
答案是不一定的,在不是所有元素都进栈的情况下,先进去的元素也可以出栈,保证是栈顶元素出栈就可以
举例,如果我们有1、2、3三个数字一次进栈,会有哪些出栈次序呢?
- 第一种:1、2、3进,再3、2、1出,出栈次序为321
- 第二种:1进,1出,2进,2出,3进,3出。进一个出一个,出栈次序为123
- 第三种,1进,2进,2出,1出,3进,3出,出栈顺序为213
- 第四种:1进,1出,2进,3进,3出,2出,出栈顺序为132
- 第五种:1进,2进,2出,3进,3出,1出,出栈次序为231
栈的顺序存储结构的有关操作
对于栈来讲,线性表的操作特性它都具备,由于它的特殊性,特别是插入和删除操作,我们改名为push和pop
线性表是用数组来实现的,对于栈这一种只能一头插入的线性表来说,下表为0的一段作为栈底
栈的结构定义与初始化
typedef int STDataType;typedef struct Stack
{STDataType* a;int top;int capacity;
}ST;
对栈进行初始化,构造initial函数
void StackInit(ST* ps)
{assert(ps);ps->a = NULL;ps->top = -1;ps->capacity = 0;}
首先assert断言ps是否为空指针,将a指向NULL,capacity置为0,而top置为-1
在栈的实现中,top变量一般用来指示栈顶元素的位置。对于一个空栈来说,不存在任何元素,因此没有一个合理的位置可以被称为栈顶。在这种情况下,需要一个特殊的值来表示栈是空的
在进行入栈和出栈操作时,top的更新逻辑变得简单直接。例如,每当添加一个新元素到栈中时,先将top加1(这将把top从-1改为0,表示第一个元素的位置),然后在top对应的位置上存放新元素
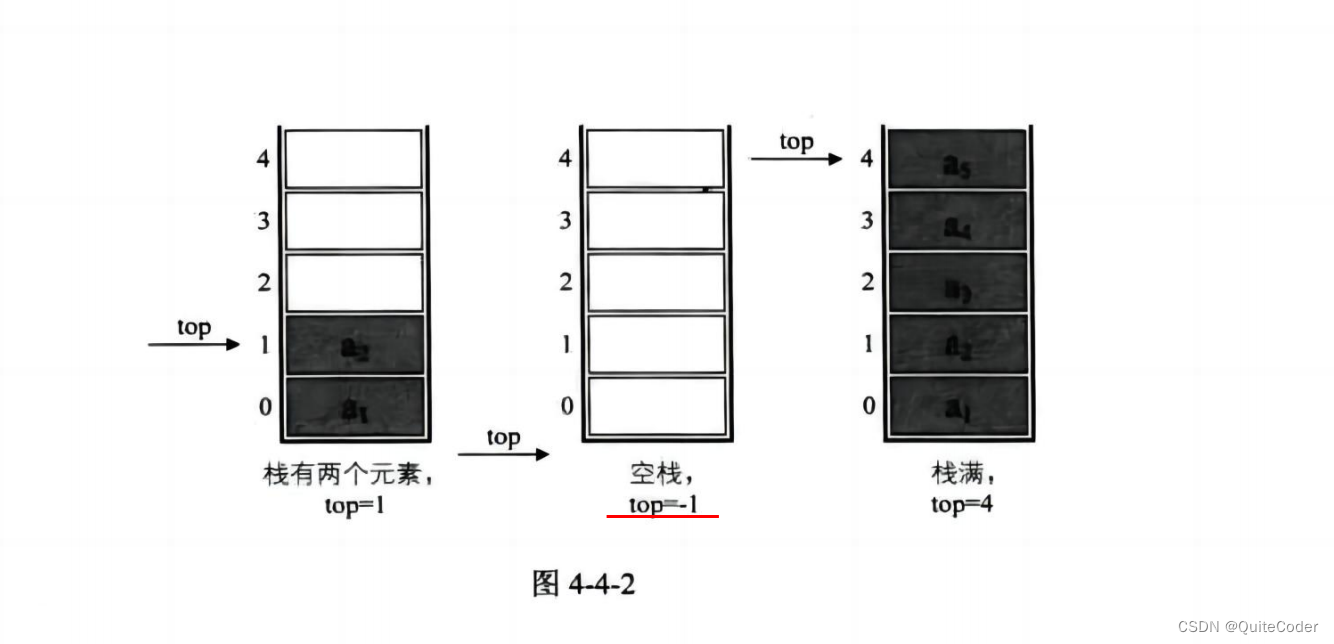
保证top指向栈顶元素
压栈操作
void StackPush(ST* ps, STDataType x) {assert(ps != NULL); // 检查栈是否已满if (ps->top + 1 == ps->capacity) {int newcapacity=ps->capacity==0?4:ps->capacity*2; STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * newcapacity);if (tmp == NULL) {perror("realloc fail");return;}ps->a = tmp;ps->capacity = newcapacity;}// 先将栈顶索引top增加1,然后在新的栈顶位置存入元素xps->top++;ps->a[ps->top] = x;
}
- 首先检查栈是否已满,即:
if (ps->top + 1 == ps->capacity)。这是通过比较top + 1(即如果添加新元素后的栈顶索引)和capacity(栈的容量)来实现的。 - 如果栈满,执行扩容操作。新的容量newcapacity为当前容量的两倍,但如果当前容量为0,则初始化容量为4。
- 使用realloc尝试扩容
- 栈顶索引top增加1,以便于在正确的位置添加新元素。
- 在新的栈顶位置存入元素x,即
ps->a[ps->top] = x;
出栈操作
void StackPop(ST* ps) {assert(ps != NULL); if (ps->top == -1) { printf("栈已空,无法执行出栈操作。\n");return;}ps->top -= 1;
}
两个操作没有涉及任何循环,时间复杂度均为O(1);
获取栈顶元素和有效元素个数
STDataType StackTop(ST* ps) {assert(ps != NULL);if (ps->top == -1) {printf("错误:试图从空栈中获取元素。\n");exit(EXIT_FAILURE); }return ps->a[ps->top];
}
int StackSize(ST* ps) {assert(ps != NULL); return ps->top + 1;
}
判断是否为空和栈的销毁
bool StackEmpty(ST* ps) {assert(ps != NULL); return ps->top == -1;
}
在C语言中,当一个函数的返回类型被声明为bool(需要包含<stdbool.h>头文件),那么它只能返回两个值之一:true或false。
- true通常被定义为整数1。
- false被定义为整数0。
这意味着,当你看到一个函数的返回类型是bool,你可以期望该函数根据其执行的操作或检查的条件,返回表示“真”或者“假”的结果。这样的函数通常用于进行某种条件检测或确认某事是否成立。
这行代码核心地检查栈是否为空。在这里,ps->top是栈顶元素的索引。通常情况下,当栈为空时,栈顶索引top被设置为-1来表示栈内没有元素。如果ps->top等于-1,函数返回true,表示栈为空;否则返回false,表示栈中有元素。
void StackDestroy(ST* ps) {assert(ps != NULL); // 确保栈指针ps非空free(ps->a); // 释放动态数组ps->a = NULL; // 将指针设为NULL,防止悬挂指针ps->top = -1; // 重置栈顶指标ps->capacity = 0; // 重置栈容量
}
栈的链式存储结构的有关操作
讲完了栈的顺序存储,我们接着来看栈的链式存储
思考一下,栈只在栈顶进行删除和插入,那么栈顶是放在链表的头端还是尾端呢?
当使用链表实现链式栈时,通常选择链表的头部作为栈顶,因为这种方法更高效、实现也更简单:
- 在链表头部插入或删除节点只需要O(1)的时间复杂度,因为这些操作不需要遍历整个链表。这对于栈操作(即push和pop操作)非常理想,因为它们也应该是O(1)的时间复杂度
- 链表有头指针,栈有顶部指针,可以做到合二为一
链表的创建
typedef int STDataType;typedef struct StackNode {STDataType data; struct StackNode* next;
} StackNode;
链式栈的定义
typedef struct LinkedStack{StackNode* top; int size;
} LinkedStack;
初始化
初始化一个空栈,只需要将栈顶指针设置为NULL,栈的大小设置为0
void Initialize(LinkedStack* stack) {stack->top = NULL;stack->size = 0;
}
压栈和出栈
void Push(LinkedStack* stack, STDataType x) {StackNode* newNode = (StackNode*)malloc(sizeof(StackNode));if (newNode == NULL) {printf("Memory allocation failed\n");return;}newNode->data = x ;newNode->next = stack->top; // 新节点的下一个节点就是当前的栈顶stack->top = newNode; // 更新栈顶为新节点stack->size++;
}
推入新元素需要创建一个新的节点,并将其插入到链表的头部。
int Pop(LinkedStack* stack) {if (stack->top == NULL) { // 检查栈是否为空printf("Stack is empty\n");return -1; // 使用-1表示错误情况,实际使用中应考虑其他错误处理方式}StackNode* temp = stack->top; // 临时保存栈顶节点int data = temp->data; // 获取栈顶数据stack->top = temp->next; // 更新栈顶指针为下一个节点free(temp); // 释放原栈顶节点的内存stack->size--;return data; // 返回栈顶数据
}
弹出栈顶元素先要检查栈是否为空。如果不为空,将栈顶节点从链表中移除,并释放它所占用的内存。
检查栈是否为空
检查链式栈是否为空也很简单,只需检查栈顶指针是否为NULL。
int IsEmpty(LinkedStack* stack) {return stack->top == NULL;
}
栈的应用–有效的扩号
给定一个只包括 ‘(’,‘)’,‘{’,‘}’,‘[’,‘]’ 的字符串 s ,判断字符串是否有效。
有效字符串需满足:
- 左括号必须用相同类型的右括号闭合。
- 左括号必须以正确的顺序闭合。
- 每个右括号都有一个对应的相同类型的左括号。
这个问题可以通过使用栈来轻松解决。基本思想是遍历字符串中的每个字符,对于每个开放括号((, {, [),我们将其推入栈中。对于每个关闭括号(), }, ]),我们检查它是否与栈顶的开放括号匹配。如果匹配,则弹出栈顶元素并继续处理字符串的下一个字符。如果在任何时候遇到不匹配的情况,或者在遍历完字符串后栈不为空,则字符串不是有效的
typedef char STDataType;typedef struct Stack
{STDataType* a;int top;int capacity;
}ST; void StackInit(ST* ps)
{assert(ps);ps->a = NULL;ps->top = -1;ps->capacity = 0;}void StackPush(ST* ps, STDataType x) {assert(ps != NULL); if (ps->top + 1 == ps->capacity) {int newcapacity=ps->capacity==0?4:ps->capacity*2;STDataType* tmp = (STDataType*)realloc(ps->a, sizeof(STDataType) * newcapacity);if (tmp == NULL) {perror("realloc fail");return;}ps->a = tmp;ps->capacity = newcapacity;}ps->top += 1;ps->a[ps->top] = x;
}
void StackPop(ST* ps) {assert(ps != NULL); if (ps->top == -1) {printf("栈已空,无法执行出栈操作。\n");return;}ps->top -= 1;
}
STDataType StackTop(ST* ps) {assert(ps != NULL); if (ps->top == -1) {printf("错误:试图从空栈中获取元素。\n");exit(EXIT_FAILURE); }return ps->a[ps->top];
}
int StackSize(ST* ps) {assert(ps != NULL); return ps->top + 1;
}
bool StackEmpty(ST* ps) {assert(ps != NULL); return ps->top == -1;
}
void StackDestroy(ST* ps) {assert(ps != NULL); free(ps->a); ps->a = NULL; ps->top = -1; ps->capacity = 0;
}
我们首先列出准备好的函数,这里的数据类型为字符类型,只需要将typedef int STDataType;改为typedef char STDataType;
bool isValid(char* s)
{ST sa;StackInit(&sa);while(*s){if(*s=='['||*s=='{'||*s=='('){StackPush(&sa,*s);}else{if(StackEmpty(&sa))return false;char top=StackTop(&sa);StackPop(&sa);if(*s==']'&& top!='['||*s=='}'&&top!='{'||*s==')'&&top!='('){return false;}}++s;}bool ret =StackEmpty(&sa);StackDestroy(&sa);return ret;
}
使用while(*s)循环遍历字符串s中的每个字符。对于每个字符有两种情况:
- 左括号(
[, {, ():如果字符是左括号之一,使用StackPush(&sa,*s);将其推入栈中。 - 右括号(
], }, )):如果字符是右括号,首先检查栈是否为空,如果空,则立即返回false,表示没有对应的左括号与当前右括号匹配。如果栈不为空,则获取栈顶元素top=StackTop(&sa);并使用StackPop(&sa);将其从栈中弹出。然后检查栈顶元素是否与当前的右括号匹配,如果不匹配,则返回false。 - 结束条件:遍历结束后,使用
bool ret =StackEmpty(&sa);检查栈是否为空。如果栈为空,意味着所有的左括号都已被正确匹配,返回true;否则,返回false。最后,StackDestroy(&sa);销毁栈以释放可能分配的资源
本节内存到此结束!感谢大家的阅读!
相关文章:

数据结构与算法:栈
朋友们大家好啊,在链表的讲解过后,我们本节内容来介绍一个特殊的线性表:栈,在讲解后也会以例题来加深对本节内容的理解 栈 栈的介绍栈进出栈的变化形式 栈的顺序存储结构的有关操作栈的结构定义与初始化压栈操作出栈操作获取栈顶元…...

Newtonsoft.Json设置忽略某些字段
using Newtonsoft.Json; using Newtonsoft.Json.Serialization; using System; using System.Collections.Generic; using System.Linq; using System.Text; using System.Threading.Tasks;namespace TestProject1 {/// <summary>/// 输出json时,设置忽略哪些…...

【c++每天一题】跳跃游戏
题目 给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。 示例 1࿱…...

【C# 中抓取包含多个屏幕内容的整个桌面】
要在 C# 中抓取包含多个屏幕内容的整个桌面,可以使用 .NET Framework 或者其他第三方库来实现。一种常见的方法是使用 System.Windows.Forms 和 System.Drawing 命名空间中的类来实现屏幕截图。以下是一个示例代码,演示如何抓取包含多个屏幕内容的整个桌…...
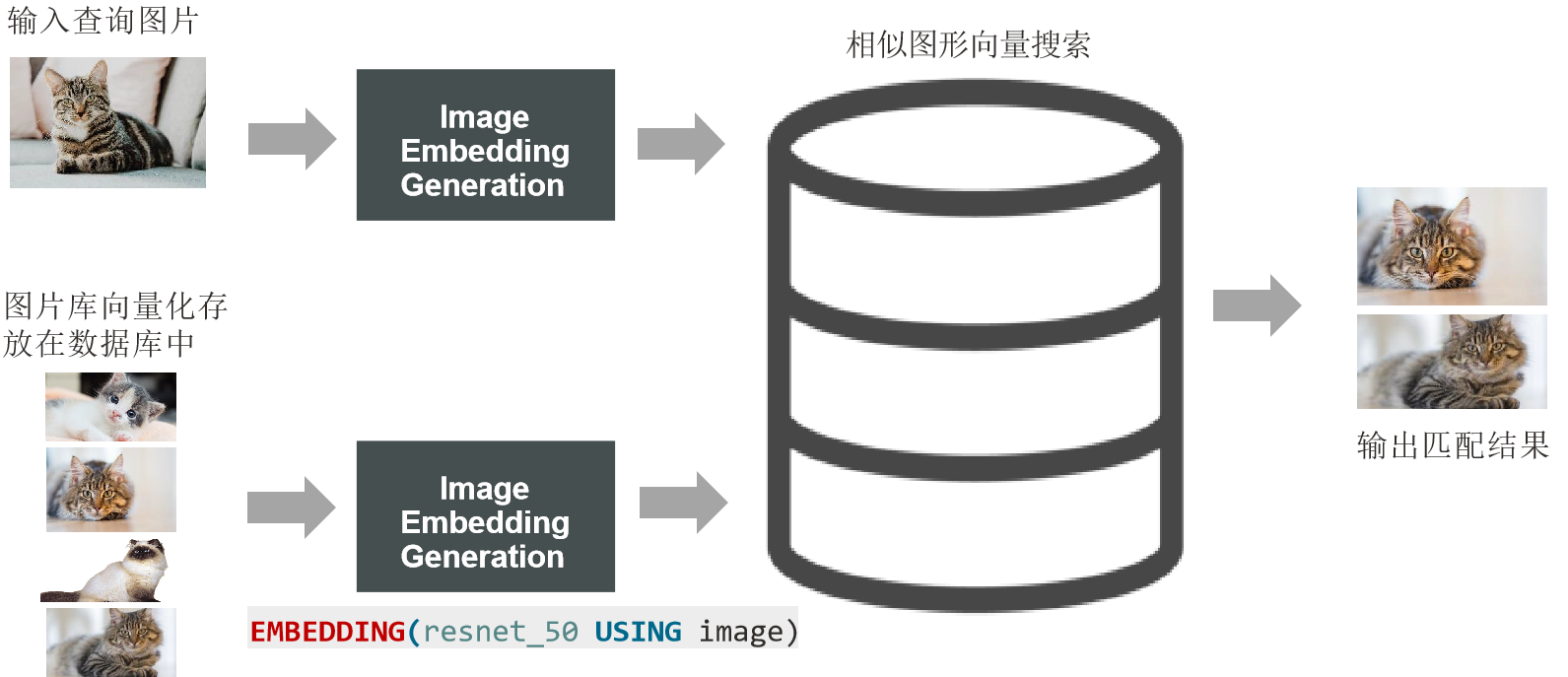
数据库管理-第152期 Oracle Vector DB AI-04(20240220)
数据库管理152期 2024-02-20 数据库管理-第152期 Oracle Vector DB & AI-04(20240220)1 常用的向量检索方法聚类图搜索哈希量化 2 Oracle Vector DB中的索引索引(默认) 索引(高级)3 EMBEDDINGSSQL EMBE…...

uniapp app端水印组件封装 一次引入版
直接上代码 <template><view><canvas canvas-id"myCanvas"style"width: 100vw; height: 100vh;opacity: 0;position: fixed;top: -1000px;"></canvas></view> </template><script>export default {name: "…...

最新Unity游戏主程进阶学习大纲(2个月)
过完年了,很多同学开始重新规划自己的职业方向,找更好的机会,准备升职或加薪。今天给那些工作了1~5年的开发者梳理”游戏开发客户端主程”的学习大纲,帮助大家做好面试准备。适合Unity客户端开发者。进阶主程其实就是从固定的几个方面搭建好完整的知识体…...

NoSQL 数据库管理工具,搭载强大支持:Redis、Memcached、SSDB、LevelDB、RocksDB,为您的数据存储提供无与伦比的灵活性与性能!
NoSQL 数据库管理工具,搭载强大支持:Redis、Memcached、SSDB、LevelDB、RocksDB,为您的数据存储提供无与伦比的灵活性与性能! 【官网地址】:http://www.redisant.cn/nosql 介绍 直观的用户界面 从单一应用程序中同…...

基于Spring Boot的多级缓存系统设计
在构建大规模应用时,缓存系统是提高性能的关键因素之一。为了更有效地利用缓存,我们可以设计一个基于Spring Boot的多级缓存系统,结合本地内存缓存(如Caffeine)和分布式缓存(如Redis)。以下是一…...

k8s-配置与存储-配置管理
文章目录 一、配置存储1.1 ConfigMap1.1.1.基于文件夹的创建方式1.1.2指定文件的创建方式1.1.3 配置文件创建configmap 1.2 Secret1.2.1Secret的应用与Docker仓库 Secret设置1. Kubernetes 中的 Secrets:创建 Secret 示例:将 Secret 挂载到 Pod 中的示例…...

c语言实现bellman-ford算法
下面是使用C语言实现Bellman-Ford算法的示例代码。Bellman-Ford算法用于在带权重的图中找到从单个源点到所有其他顶点的最短路径,它也能处理图中包含负权重边的情况。 #include <stdio.h> #include <stdlib.h> #include <limits.h>// 定义边的结构 struct …...

socket与rpc的区别
如今的游戏开发,不搞个跨服玩法都不好意思说在做游戏了(当然,也跟游戏类型有关,一些轻度休闲游戏可以排除在外)。跨服玩法的设计,可以进一步激发玩家追求高战力的虚荣心,也可以汇聚玩家数量&…...
10、内网安全-横向移动域控提权NetLogonADCSPACKDC永恒之蓝
用途:个人学习笔记,有所借鉴,欢迎指正! 背景: 主要针对内网主机中的 域控提权漏洞,包含漏洞探针和漏洞复现利用。 1、横向移动-系统漏洞-CVE-2017-0146(ms17-010,永恒之蓝࿰…...

代码随想录算法训练营第三八天 | 动态规划
目录 动态规划基础斐波那契数爬楼梯使用最小花费爬楼梯 LeetCode 509. 斐波那契数 LeetCode 70. 爬楼梯 LeetCode 746. 使用最小花费爬楼梯 动态规划基础 Dynamic Programming (DP) 如果某一问题有很多重叠子问题,使用动态规划是最有效的。 动态规划中每一个状态…...
【ubuntu2004安装N卡驱动】
软硬件环境 硬件:联想notebook16,显卡4060laptop 软件: ubuntu20.04 驱动安装成功的版本:NVIDIA-Linux-x86_64-535.146.02.run 使用默认的驱动安装,没用原因如下 让手动安装。 手动安装 环境准备: sudo …...
使用 Docker 安装 Kibana 8.4.3
使用 Docker 安装 Kibana 8.4.3 一. 安装启动 Kibana 8.4.3二. 简单使用2.1 向 Elasticsearch 发送请求2.2 搜索2.3 整体页面 前言 这是我在这个网站整理的笔记,有错误的地方请指出,关注我,接下来还会持续更新。 作者:神的孩子都在歌唱 安装k…...

基于python社交网络大数据分析系统的设计与实现
项目:基于python社交网络大数据分析系统的设计与实现 摘 要 社交网络大数据分析系统是一种能自动从网络上收集信息的工具,可根据用户的需求定向采集特定数据信息的工具,本项目通过研究爬取微博网来实现社交网络大数据分析系统功能。对于采集…...

【设计模式】23种设计模式笔记
设计模式分类 模板方法模式 核心就是设计一个部分抽象类。 这个类具有少量具体的方法,和大量抽象的方法,具体的方法是为外界提供服务的点,具体方法中定义了抽象方法的执行序列 装饰器模式 现在有一个对象A,希望A的a方法被修饰 …...

编程笔记 Golang基础 009 标识符和关键字
编程笔记 Golang基础 009 标识符和关键字 一、标识符二、标识符分类(一)空白标识符(又称下划线 _)(二)预声明标识符(三)唯一标识符(四)导出标识符 三、关键字…...

vue3中mockjs模拟获取数据
开发项目的时候,如果后端接口没有出来,前端工程师也不必非得等接口出来才进行下步开发。可以使用mock.js来模拟接口数据,以下就是使用vue3设置hook函数来封装axios请求,配合mock.js来实现的代码,mock的官网 Mock.js 一…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

MySQL账号权限管理指南:安全创建账户与精细授权技巧
在MySQL数据库管理中,合理创建用户账号并分配精确权限是保障数据安全的核心环节。直接使用root账号进行所有操作不仅危险且难以审计操作行为。今天我们来全面解析MySQL账号创建与权限分配的专业方法。 一、为何需要创建独立账号? 最小权限原则…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...
