【动态规划】【矩阵快速幂】LeetCode2851. 字符串转换
作者推荐
【深度优先搜索】【树】【有向图】【推荐】685. 冗余连接 II
涉及知识点
【矩阵快速幂】封装类及测试用例及样例
LeetCode 2851. 字符串转换
给你两个长度都为 n 的字符串 s 和 t 。你可以对字符串 s 执行以下操作:
将 s 长度为 l (0 < l < n)的 后缀字符串 删除,并将它添加在 s 的开头。
比方说,s = ‘abcd’ ,那么一次操作中,你可以删除后缀 ‘cd’ ,并将它添加到 s 的开头,得到 s = ‘cdab’ 。
给你一个整数 k ,请你返回 恰好 k 次操作将 s 变为 t 的方案数。
由于答案可能很大,返回答案对 109 + 7 取余 后的结果。
示例 1:
输入:s = “abcd”, t = “cdab”, k = 2
输出:2
解释:
第一种方案:
第一次操作,选择 index = 3 开始的后缀,得到 s = “dabc” 。
第二次操作,选择 index = 3 开始的后缀,得到 s = “cdab” 。
第二种方案:
第一次操作,选择 index = 1 开始的后缀,得到 s = “bcda” 。
第二次操作,选择 index = 1 开始的后缀,得到 s = “cdab” 。
示例 2:
输入:s = “ababab”, t = “ababab”, k = 1
输出:2
解释:
第一种方案:
选择 index = 2 开始的后缀,得到 s = “ababab” 。
第二种方案:
选择 index = 4 开始的后缀,得到 s = “ababab” 。
提示:
2 <= s.length <= 5 * 105
1 <= k <= 1015
s.length == t.length
s 和 t 都只包含小写英文字母。
矩阵快速幂
想到快速指数幂时,非常容易想到n阶方阵。n阶方阵自乘一次的时间复杂度就是O(n3),严重超时。
可以优化到2阶方阵。
操作若干次后,假定s[0]的新下标为j。则s[j,n)+s[0,j) ≡ \equiv ≡ s ,故若干操作后的状态,可以记为j。某次操作前状态为j1,操作后为j2,则 j 2 ∈ [ 0 , j 1 ) ∪ ( j 1 , n ) 即除 j 1 外的所有值 j2\in[0,j1) \cup (j1,n) \quad \quad \quad \quad\quad 即除j1外的所有值 j2∈[0,j1)∪(j1,n)即除j1外的所有值
性质一:j3 > 0 j4>0 操作若干次后,结果为j3和j4的可能数相等。
初始状态
pre[0]=1 其它为0 符合
前置状态符合pre[j3] == pre[j4],操作一次后,后置状态符合dp[3]==dp[4]。
dp[j3] = ∑ m : 0 n − 1 \Large \sum_{m:0}^{n-1} ∑m:0n−1pre(m) - pre[j3]
dp[j4] = ∑ m : 0 n − 1 \Large \sum_{m:0}^{n-1} ∑m:0n−1pre(m) - pre[j4]
dp[j3]-dp[j4] = pre[j3]-pre[j4] = 0。
动态规划的状态表示
只需要两种状态j为0,j不为0。
pre[0] = 1,pre[1]=0
动态规划的转移方程
dp[0] = pre[1](n-1)
dp[1] = pre[0] +pre[1](n-2)
超时
k的最大值是1012,大幅超时。用矩阵指数幂。
令矩阵是mat则
{ d p [ 0 ] = p r e [ 0 ] m a t [ 0 ] [ 0 ] + p r e [ 1 ] m a t [ 1 ] [ 0 ] d p [ 1 ] = p r e [ 0 ] m a t [ 0 ] [ 1 ] + p r e [ 1 ] m a t [ 1 ] [ 1 ] → [ 0 1 n − 1 n − 2 ] \begin{cases} dp[0] = pre[0]mat[0][0] + pre[1]mat[1][0] \\ dp[1] = pre[0]mat[0][1] + pre[1]mat[1][1] \\ \end{cases} \rightarrow\begin{bmatrix} 0 & 1 \\ n-1 & n-2 \\ \end{bmatrix} {dp[0]=pre[0]mat[0][0]+pre[1]mat[1][0]dp[1]=pre[0]mat[0][1]+pre[1]mat[1][1]→[0n−11n−2]
KMP
还需要判断s[j,n)和t[0,j-n) 和 s[0,j)和t[j-n,n) 是否相等。
代码
核心代码
class KMP
{
public:virtual int Find(const string& s, const string& t){CalLen(t);m_vSameLen.assign(s.length(), 0);for (int i1 = 0, j = 0; i1 < s.length(); ){for (; (j < t.length()) && (i1 + j < s.length()) && (s[i1 + j] == t[j]); j++);//i2 = i1 + j 此时s[i1,i2)和t[0,j)相等 s[i2]和t[j]不存在或相等m_vSameLen[i1] = j;//t[0,j)的结尾索引是j-1,所以最长公共前缀为m_vLen[j-1],简写为y 则t[0,y)等于t[j-y,j)等于s[i2-y,i2)if (0 == j){i1++;continue;}const int i2 = i1 + j;j = m_vLen[j - 1];i1 = i2 - j;//i2不变}for (int i = 0; i < m_vSameLen.size(); i++){//多余代码是为了增加可测试性if (t.length() == m_vSameLen[i]){return i;}}return -1;}vector<int> m_vSameLen;//m_vSame[i]记录 s[i...]和t[0...]最长公共前缀,增加可调试性static vector<int> Next(const string& s){const int len = s.length();vector<int> vNext(len, -1);for (int i = 1; i < len; i++){int next = vNext[i - 1];while ((-1 != next) && (s[next + 1] != s[i])){next = vNext[next];}vNext[i] = next + (s[next + 1] == s[i]);}return vNext;}
protected:void CalLen(const string& str){m_vLen.resize(str.length());for (int i = 1; i < str.length(); i++){int next = m_vLen[i - 1];while (str[next] != str[i]){if (0 == next){break;}next = m_vLen[0];}m_vLen[i] = next + (str[next] == str[i]);}}int m_c;vector<int> m_vLen;//m_vLen[i] 表示t[0,i]的最长公共前后缀
};template<int MOD = 1000000007>
class C1097Int
{
public:C1097Int(long long llData = 0) :m_iData(llData% MOD){}C1097Int operator+(const C1097Int& o)const{return C1097Int(((long long)m_iData + o.m_iData) % MOD);}C1097Int& operator+=(const C1097Int& o){m_iData = ((long long)m_iData + o.m_iData) % MOD;return *this;}C1097Int& operator-=(const C1097Int& o){m_iData = (m_iData + MOD - o.m_iData) % MOD;return *this;}C1097Int operator-(const C1097Int& o){return C1097Int((m_iData + MOD - o.m_iData) % MOD);}C1097Int operator*(const C1097Int& o)const{return((long long)m_iData * o.m_iData) % MOD;}C1097Int& operator*=(const C1097Int& o){m_iData = ((long long)m_iData * o.m_iData) % MOD;return *this;}bool operator<(const C1097Int& o)const{return m_iData < o.m_iData;}C1097Int pow(long long n)const{C1097Int iRet = 1, iCur = *this;while (n){if (n & 1){iRet *= iCur;}iCur *= iCur;n >>= 1;}return iRet;}C1097Int PowNegative1()const{return pow(MOD - 2);}int ToInt()const{return m_iData;}
private:int m_iData = 0;;
};class CMat
{
public:// 矩阵乘法static vector<vector<long long>> multiply(const vector<vector<long long>>& a, const vector<vector<long long>>& b) {const int r = a.size(), c = b.front().size(), iK = a.front().size();assert(iK == b.size());vector<vector<long long>> ret(r, vector<long long>(c));for (int i = 0; i < r; i++){for (int j = 0; j < c; j++){for (int k = 0; k < iK; k++){ret[i][j] = (ret[i][j] + a[i][k] * b[k][j]) % s_llMod;}}}return ret;}// 矩阵快速幂static vector<vector<long long>> pow(const vector<vector<long long>>& a, vector<vector<long long>> b, long long n) {vector<vector<long long>> res = a;for (; n; n /= 2) {if (n % 2) {res = multiply(res, b);}b = multiply(b, b);}return res;}static vector<vector<long long>> TotalRow(const vector<vector<long long>>& a){vector<vector<long long>> b(a.front().size(), vector<long long>(1, 1));return multiply(a, b);}
protected:const static long long s_llMod = 1e9 + 7;
};class Solution {
public:int numberOfWays(string s, string t, long long k) {const int n = s.length();KMP kmp1,kmp2;kmp1.Find(t, s);kmp2.Find(s, t);vector<bool> vSame(n);for (int j = 0; j < n; j++){if (kmp1.m_vSameLen[j] >= (n - j)){// t[j,n) == s[0,n-j)if ((0==j)||(kmp2.m_vSameLen[n-j] >= j )){//s[n-j,n) == t[0,j)vSame[j] = true;}}}vector<vector<long long >> mat = { {0,1},{n-1,n-2} };vector<vector<long long >> pre = { {1,0} };auto res = CMat::pow(pre, mat, k);C1097Int<> biRet;for (int i = 0; i < n; i++){if (vSame[i]){biRet += res[0][0 != i];}}return biRet.ToInt();}
};
测试用例
template<class T,class T2>
void Assert(const T& t1, const T2& t2)
{assert(t1 == t2);
}template<class T>
void Assert(const vector<T>& v1, const vector<T>& v2)
{if (v1.size() != v2.size()){assert(false);return;}for (int i = 0; i < v1.size(); i++){Assert(v1[i], v2[i]);}}int main()
{ string s,t;long long k = 0;{Solution sln;s = "abcd", t = "cdab", k = 2;auto res = sln.numberOfWays(s, t, k);Assert(res,2);}{Solution sln;s = "ababab", t = "ababab", k = 1;auto res = sln.numberOfWays(s, t, k);Assert(res, 2);}}
2023年9月
class KMP
{
public:
virtual int Find(const string& s,const string& t )
{
CalLen(t);
m_vSameLen.assign(s.length(), 0);
for (int i1 = 0, j = 0; i1 < s.length(); )
{
for (; (j < t.length()) && (i1 + j < s.length()) && (s[i1 + j] == t[j]); j++);
//i2 = i1 + j 此时s[i1,i2)和t[0,j)相等 s[i2]和t[j]不存在或相等
m_vSameLen[i1] = j;
//t[0,j)的结尾索引是j-1,所以最长公共前缀为m_vLen[j-1],简写为y 则t[0,y)等于t[j-y,j)等于s[i2-y,i2)
if (0 == j)
{
i1++;
continue;
}
const int i2 = i1 + j;
j = m_vLen[j - 1];
i1 = i2 - j;//i2不变
}
for (int i = 0; i < m_vSameLen.size(); i++){//多余代码是为了增加可测试性if (t.length() == m_vSameLen[i]){return i;}}return -1;
}
vector<int> m_vSameLen;//m_vSame[i]记录 s[i...]和t[0...]最长公共前缀,增加可调试性
protected:
void CalLen(const string& str)
{
m_vLen.resize(str.length());
for (int i = 1; i < str.length(); i++)
{
int next = m_vLen[i-1];
while (str[next] != str[i])
{
if (0 == next)
{
break;
}
next = m_vLen[0];
}
m_vLen[i] = next + (str[next] == str[i]);
}
}
int m_c;
vector m_vLen;//m_vLen[i] 表示t[0,i]的最长公共前后缀
};
class CMat
{
public:
// 矩阵乘法
static vector<vector> multiply(vector<vector>& a, vector<vector>& b) {
vector<vector> c(2, vector(2));
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
c[i][j] = (a[i][0] * b[0][j] + a[i][1] * b[1][j]) % s_llMod;
}
}
return c;
}
// 矩阵快速幂
static vector<vector> pow(vector<vector>& a, long long n) {
vector<vector> res = { {1, 0}, {0, 1} };
for (; n; n /= 2) {
if (n % 2) {
res = multiply(res, a);
}
a = multiply(a, a);
}
return res;
}
protected:
const static long long s_llMod = 1e9 + 7;
};
class Solution {
public:
int numberOfWays(string s, string t, long long k) {
int n = s.length();
KMP kmp1,kmp2;
kmp1.Find(s, t);
kmp2.Find(t, s);
int good = 0; //好下标的次数
for (int i = 0; i < n; i++)
{
const int leftLen = n - i;
if (kmp1.m_vSameLen[i] != leftLen)
{
continue;
}
const int rightLen = n - leftLen;
if ((0 == rightLen)|| (kmp2.m_vSameLen[n-rightLen] == rightLen ))
{
good++;
}
}
vector<vector> mat = { {good - 1,n-good},{good,n-good - 1} };
const int iGoodFirst = good - (s == t);//改变一次后,好下标的数量
vector<vector> vRes = { {iGoodFirst,n - iGoodFirst - 1},{0,0} };
k–;
auto matk = CMat::pow(mat,k);
vRes = CMat::multiply(vRes, matk);
return vRes[0][0];
}
};

扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关
下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【动态规划】【矩阵快速幂】LeetCode2851. 字符串转换
作者推荐 【深度优先搜索】【树】【有向图】【推荐】685. 冗余连接 II 涉及知识点 【矩阵快速幂】封装类及测试用例及样例 LeetCode 2851. 字符串转换 给你两个长度都为 n 的字符串 s 和 t 。你可以对字符串 s 执行以下操作: 将 s 长度为 l (0 <…...

【LeetCode每日一题】单调栈 402 移掉k位数字
402. 移掉 K 位数字 给你一个以字符串表示的非负整数 num 和一个整数 k ,移除这个数中的 k **位数字,使得剩下的数字最小。请你以字符串形式返回这个最小的数字。 示例 1 : 输入:num "1432219", k 3 输出ÿ…...

力扣 309. 买卖股票的最佳时机含冷冻期
题目来源:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-cooldown/description/ C题解:动态规划 状态1:表示持有股票。更新为之前持有股票(dp[i-1][0])或者不持有股票且不处于冷冻期后买入&…...

2024年刷题记录
马上要开始找实习了,又开始重启刷题计划了!加油冲冲冲!刷题的顺序follow代码随想录的60天刷题计划!感谢FuCosmo的总结!之前都是按照C的语法进行刷题的,这次也同样使用C。 Day 1 数组 这些题过年前都刷过了…...

【JGit 】简述及学习资料整理
JGit 介绍 [官网](JGit | The Eclipse Foundation): https://www.eclipse.org/jgit/ 用户指南 : https://github.com/eclipse-jgit/jgit/wiki/User-Guide JGit是一个用于Java编程语言的开源Git实现。它提供了一组Java库和API,使开发人员可以在他们的Java应用程序…...

python数据类型-集合set
1 集合(set)的定义 1.1 集合是一个无序且不重复元素的序列: 1)无序:存储顺序和添加的顺序不一定相同,不支持索引、切片 2)元素不重复:当添加重复元素时,集合会自动去重…...

excel如何指定求和
在Excel中,你可以使用函数来实现动态求和,使得当指定行的数值更新后,和也随之更新。具体来说,你可以使用SUM函数结合一些动态的引用方法。以下是一种实现方式: 假设你要对A列(从A1到A10,以示例…...
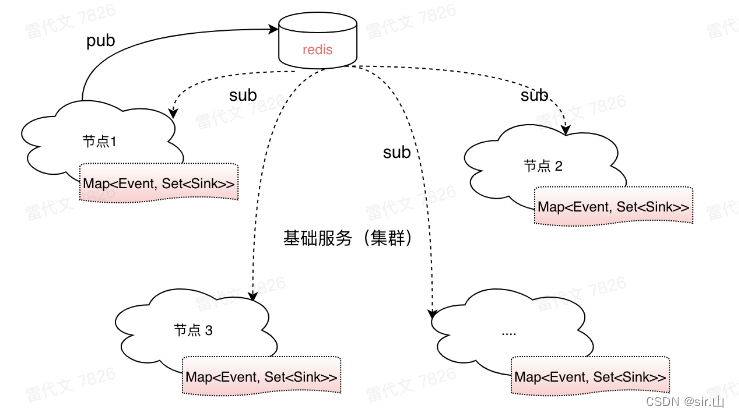
服务端实时推送技术之SSE(Server-Send Events)
文章目录 前言一、解决方案:1、传统实时处理方案:2、HTML5 标准引入的实时处理方案:3、第三方推送: 二、SSE1.引入库1、客户端: 2.服务端:三、业务实践:能否做到精准投递? 总结 前言…...
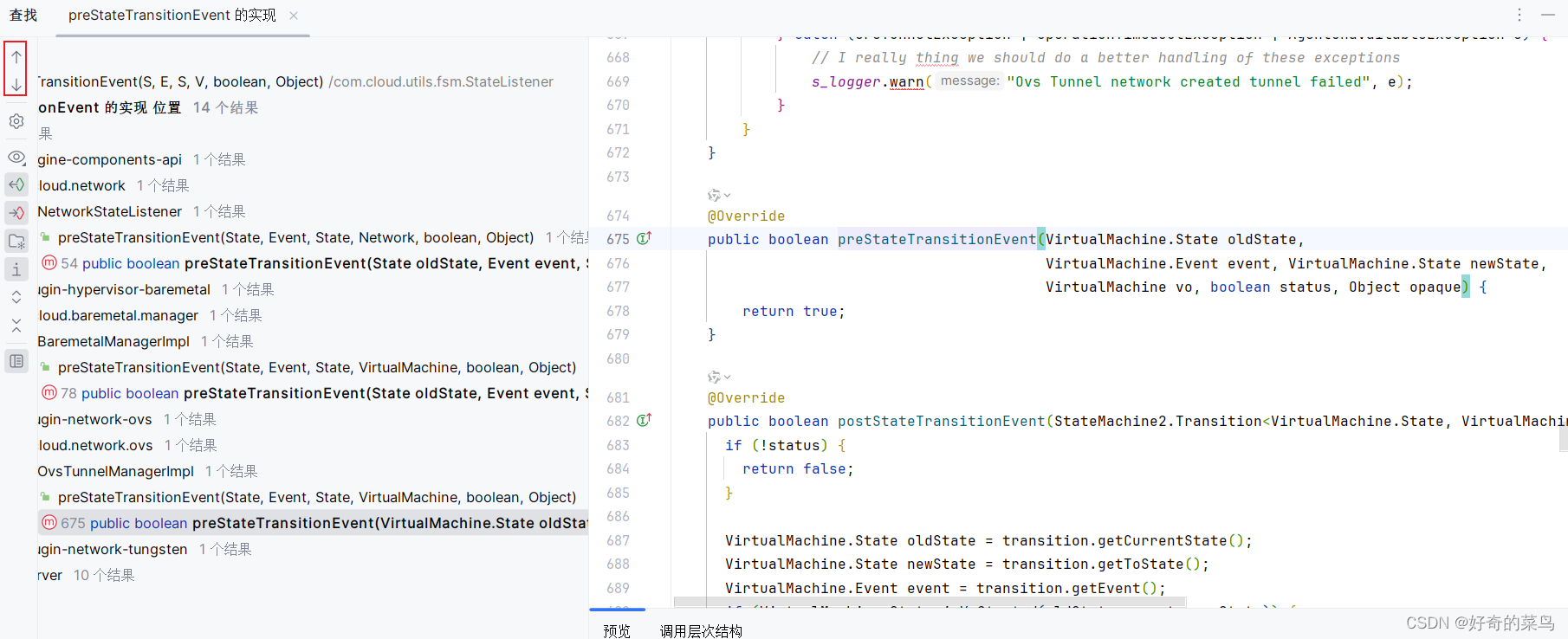
使用IntelliJ IDEA查看接口的全部实现方法
在大型Java项目中,经常会使用接口和抽象类进行代码设计。为了更好地了解代码结构和功能,我们需要快速查看一个接口的所有实现类。IntelliJ IDEA提供了一些方便的方法来实现这一目标。 1. 点击查看接口的实现子类 在IDEA中,你可以轻松地查看…...

阿里云幻兽帕鲁服务器操作系统类型怎么选择?
使用阿里云服务器搭建幻兽帕鲁操作系统类型选Windows还是Linux?如果对Linux熟悉就选择Linux,相对于windows,Linux更少占用系统资源;如果对Linux不熟悉,首选Windows。事实上,阿里云提供的幻兽帕鲁服务器通过…...

Codeforces Round 927 (Div. 3) LR-remainders的题解
原题描述: C.LR-remains 每次测试时限:2 秒 每次测试的内存限制:256 兆字节 输入:标准输入 输出:标准输出 样例1输入: 4 4 6 3 1 4 2 LRRL 5 1 1 1 1 1 1 LLLLL 6 8 1 2 3 4 5 6 RLLLRR 1 10000 1000…...
HarmonyOS—@Observed装饰器和@ObjectLink嵌套类对象属性变化
Observed装饰器和ObjectLink装饰器:嵌套类对象属性变化 概述 ObjectLink和Observed类装饰器用于在涉及嵌套对象或数组的场景中进行双向数据同步: 被Observed装饰的类,可以被观察到属性的变化;子组件中ObjectLink装饰器装饰的状…...
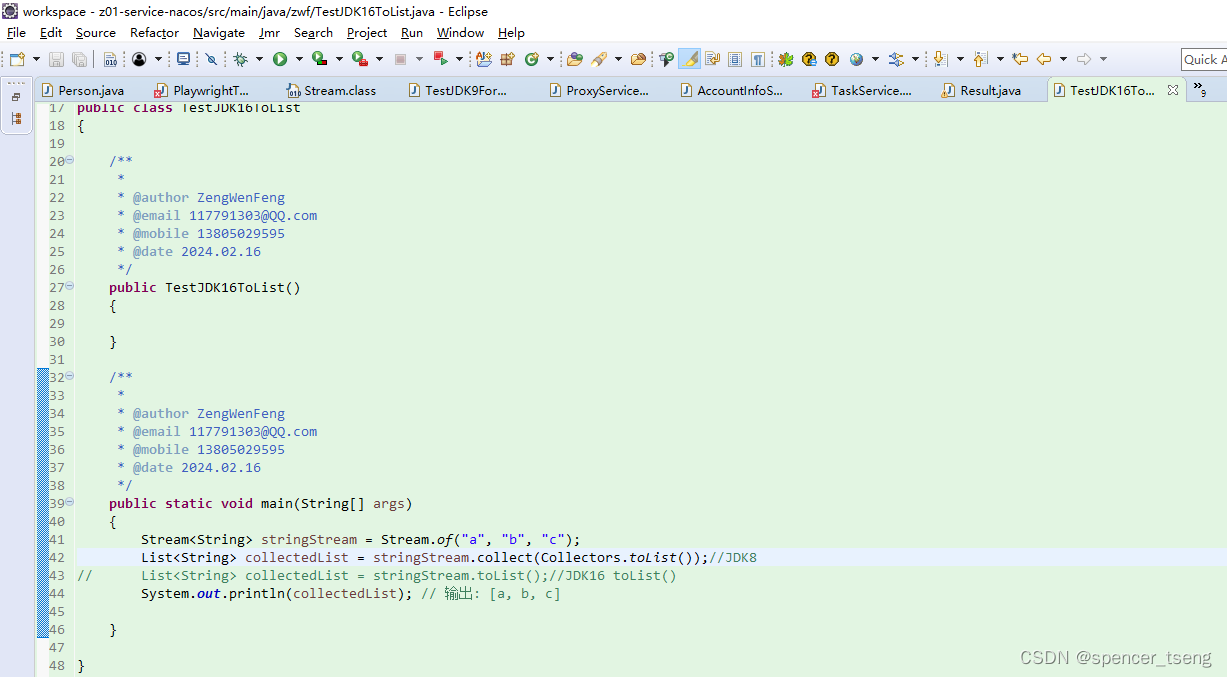
The method toList() is undefined for the type Stream
The method toList() is undefined for the type Stream (JDK16) default List<T> toList() { return (List<T>) Collections.unmodifiableList(new ArrayList<>(Arrays.asList(this.toArray()))); }...
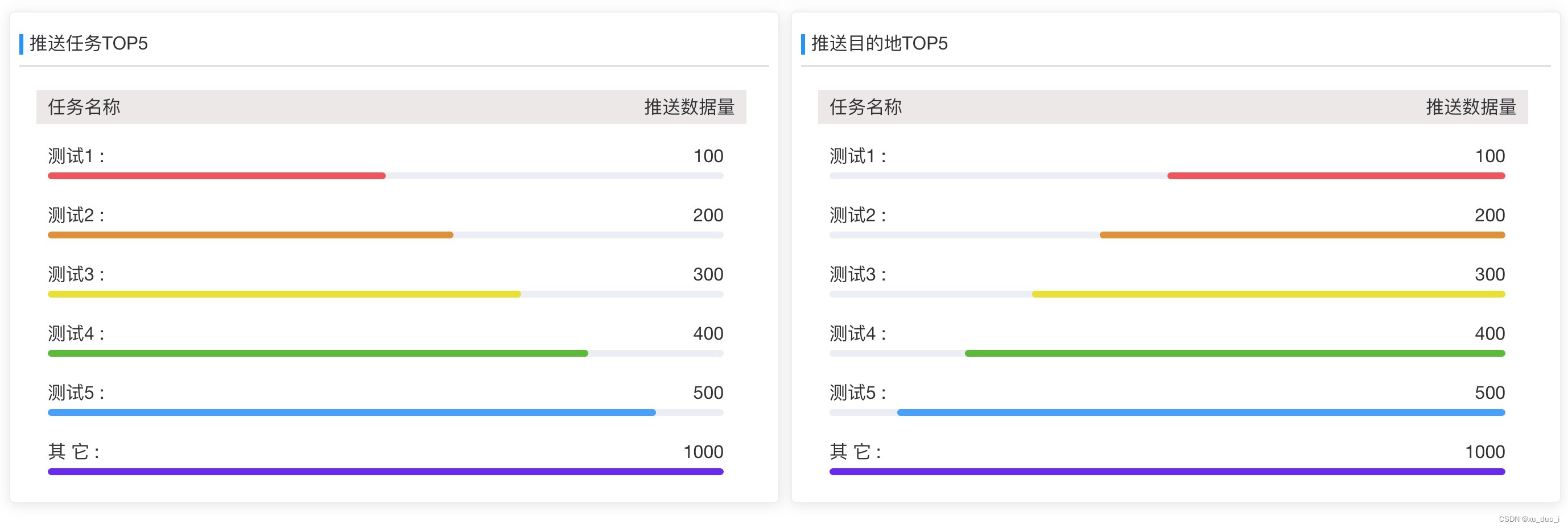
vue+element (el-progress)标签 隐藏百分比(%) ,反向显示 ,自定义颜色, demo 复制粘贴拿去用
1 效果: 2 页面代码: <el-row :gutter"10" ><el-col :span"12"><el-card ><div class"fourqu"><div><span slot"title">{{推送任务TOP5}}</span></div></div><div class&…...
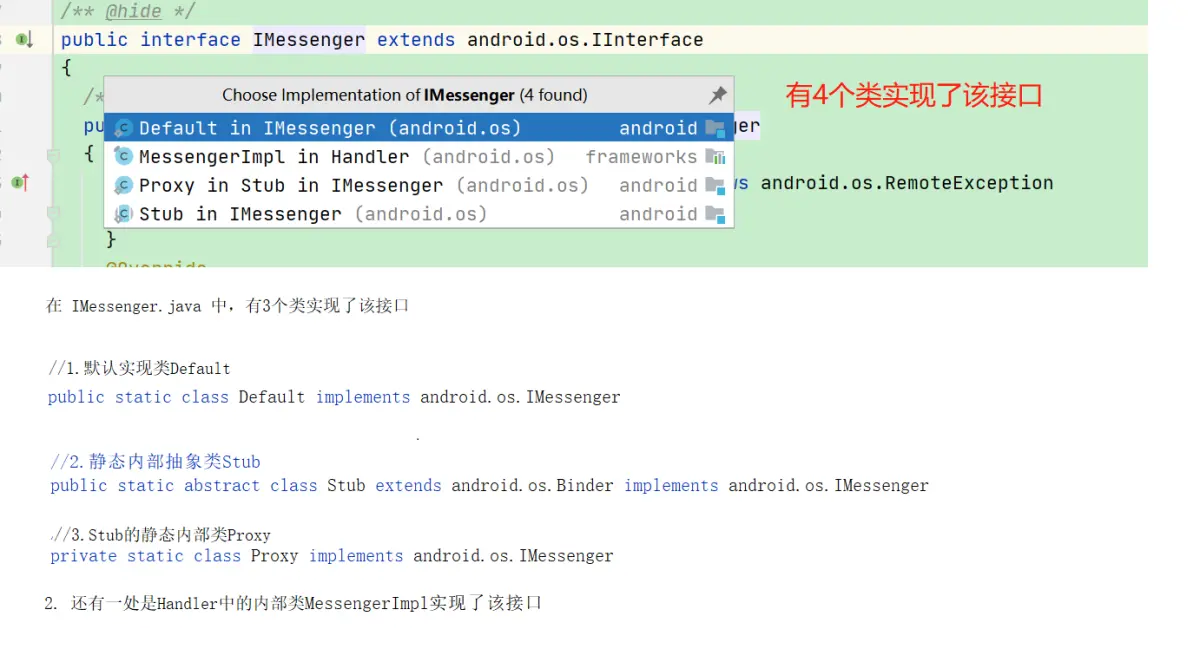
Android轻量级进程间通信Messenger源码分析
一. 概述 Android中比较有代表性的两大通信机制:1. 线程间Handler通信 2. 进程间Binder通信,本篇文章中我们在理解AIDL原理的基础上来解读一下Messenger的源代码, 并结合示例Demo加深理解。 在看本篇文章前,建议先查阅一下笔者的…...
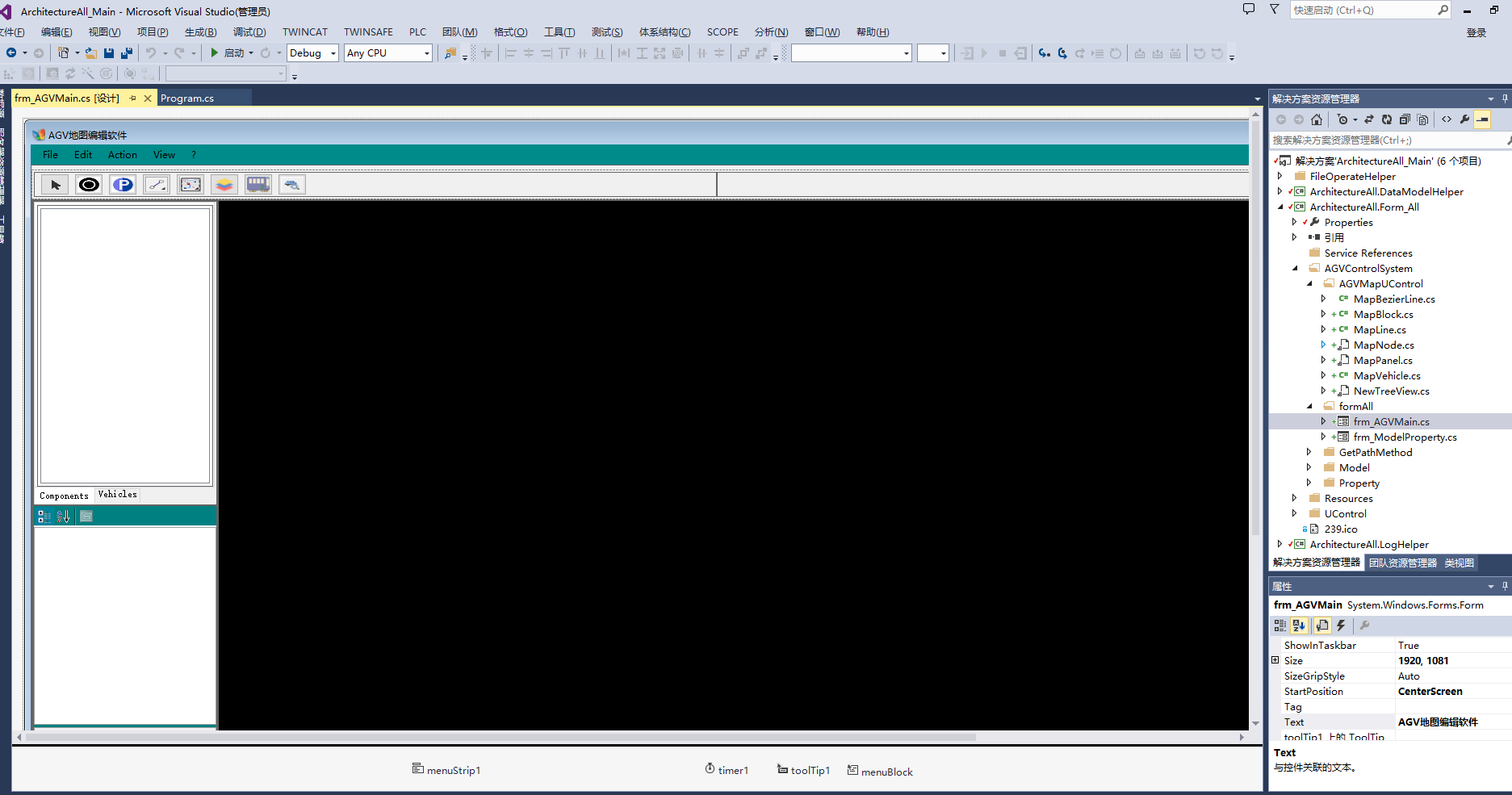
C#开发AGV地图编辑软件
C#自己开发AGV地图编辑软件: 1、自由添加和删除站点、停车位、小车、运行路径。 2、编辑得地图以XML文件保存。 3、导入编辑好地图的XML文件。 4、程序都是源码,可以直接在此基础上进行二次开发。 下载链接:https://download.csdn.net/d…...

嵌入式学习day22 Linux
文件IO: 1. lseek off_t lseek(int fd, off_t offset, int whence); 功能: 重新设定文件描述符的偏移量 参数: fd:文件描述符 offset:偏移量 whence: SEEK_SET 文件开头 …...

不确定性问题的论文笔记
Statistics starting from 01/2024, 仅列出了优秀工作中的一部分 每一年的排列顺序: CVPR, ICLR, ECCV, ICCV, ICML, AAAI, TPAMI,TIP,Arxiv 等 每周更新 2024 论文信息速览笔记是 否 已精读精读笔记Shao W, Xu Y, Peng L, et al. Failure Detection fo…...

C语言推荐书籍
本书详细讲解了C语言的基本概念和编程技巧。全书共17章。第1章、第2章介绍了C语言编程的预备知识。第3章~第15章详细讲解了C语言的相关知识,包括数据类型、格式化输入/输出、运算符、表达式、语句、循环、字符输入和输出、函数、数组和指针、字符和字符串…...

基于uniapp微信小程序的汽车租赁预约系统
随着现代汽车租赁管理的快速发展,可以说汽车租赁管理已经逐渐成为现代汽车租赁管理过程中最为重要的部分之一。但是一直以来我国传统的汽车租赁管理并没有建立一套完善的行之有效的汽车租赁管理系统,传统的汽车租赁管理已经无法适应高速发展,…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...
