备战蓝桥杯 Day11(滚动数组优化+完全背包)
01背包的滚动数组优化
【题目描述】
经典0—1背包问题,有n个物品,编号为i的物品的重量为w[i],价值为c[i],现在要从这些物品中选一些物品装到一个容量为m的背包中,使得背包内物体在总重量不超过m的前提下价值尽量大。
#include<iostream>
using namespace std;const int N = 3500, M = 12800;
int m, n, w[N], v[N], dp[M];
//状态 dp[j] 前i件物品在背包容量不超过j的情况下的最大价值
//状态转移方程 if (j >= w[i]) dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
int main() {cin >> n >> m;for (int i = 1; i <= n; i++) cin >> w[i] >> v[i];//01背包的滚动数组优化for (int i = 1; i <= n; i++){for (int j = m; j >= w[i]; j--) //01背包滚动数组优化的时候,注意j要逆推{dp[j] = max(dp[j],dp[j-w[i]]+v[i]);}}cout << dp[m] << endl;return 0;
}完全背包
特点:n种物品,每件物品有无限件(但其实是有限 m/w[i]件)
1268:【例9.12】完全背包问题
【题目描述】
设有n�种物品,每种物品有一个重量及一个价值。但每种物品的数量是无限的,同时有一个背包,最大载重量为M�,今从n�种物品中选取若干件(同一种物品可以多次选取),使其重量的和小于等于M�,而价值的和为最大。
#include<iostream>
using namespace std;const int N = 30, M = 200;
int m, n, w[N], v[N], dp[M];
//状态 dp[j] 前i种物品在背包容量不超过j的情况下的最大价值
//状态转移方程
/*
dp[j]=max{dp[j-0*w[i]]+0*v[i],dp[j-1*w[i]]+1*v[i],dp[j-2*w[i]]+2*v[i],dp[j-3*w[i]]+3*v[i],...dp[j-m/w[i]*w[i]]+m/w[i]*v[i]}
*/
int main() {cin >> m >> n;for (int i = 1; i <= n; i++) cin >> w[i] >> v[i];//完全背包朴素版本for (int i = 1; i <= n; i++)for (int j = m; j >= 1; j--)for (int k = 1; k <= m / w[i]; k++)if(j>=k*w[i]) dp[j] = max(dp[j], dp[j - k * w[i]] + k * v[i]);cout <<"max=" << dp[m] << endl;return 0;
}
多重背包
1269:【例9.13】庆功会 |
【题目描述】
为了庆贺班级在校运动会上取得全校第一名成绩,班主任决定开一场庆功会,为此拨款购买奖品犒劳运动员。期望拨款金额能购买最大价值的奖品,可以补充他们的精力和体力。
多重背包特点:n种物品,每件物品有指定数量s[i](真实数量上限:min(m/w[i],s[i]))
状态 dp[j] 前i种物品在背包容量不超过j的情况下的最大价值
int main() { cin >> n >> m;for (int i = 1; i <= n; i++) cin >> w[i] >> v[i]>>s[i];//多重背包朴素版本for (int i = 1; i <= n; i++)for (int j = m; j >= 1; j--)for (int k = 1; k <= min(m / w[i], s[i]); k++)//针对第i种物品,得到选k件的最优解if (j >= k * w[i]) dp[j] = max(dp[j], dp[j - k * w[i]] + k * v[i]);cout << dp[m] << endl;return 0;
}
相关文章:
)
备战蓝桥杯 Day11(滚动数组优化+完全背包)
01背包的滚动数组优化 【题目描述】 经典0—1背包问题,有n个物品,编号为i的物品的重量为w[i],价值为c[i],现在要从这些物品中选一些物品装到一个容量为m的背包中,使得背包内物体在总重量不超过m的前提下价值尽量大。 #include&…...

Java SE 入门到精通—4.抽象类与接口【Java】
抽象类 同接口一样,用来约束子类,限制子类必须拥有某些方法,比普通类多了个抽象方法,用抽象方法该类必为抽象类 概念 没有具体的对象,具体的方法的一个类 abstract关键字声明为抽象类/方法 一个类中有抽象方法则该…...

Python 开发转 Java 简易路线 - 更新中
有了 Python 开发基础,Java 的内容都可以快速过一遍,复杂地方跟着写一遍。 一、基础 1、Java 基础:尚硅谷 - Java基础 全部快速过一遍, 2、数据库:略。 着重 mysql 高级部分(针对面试)&…...

Python编程语言学习
1.Python 特点 Python是一种简单、易读、易学和高效的编程语言,具有以下特点: 简单易学:Python采用清晰简洁的语法,注重代码的可读性和可维护性,使得初学者能够快速上手并编写出清晰的代码。 面向对象:Py…...
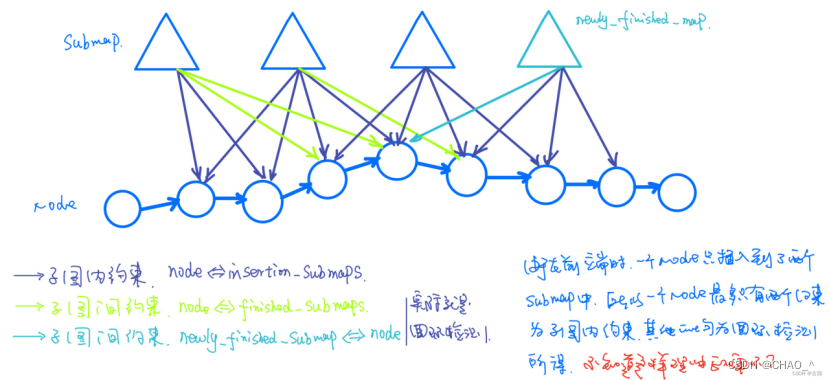
Cartographer框架简述
catographer框架分为前端和后端 前端包括雷达数据处理;位姿预测;扫描匹配和栅格地图更新。 后端包括后端:线程池任务与调度;向位姿图添加节点,计算节点的子图内约束和子图间约束(回环检测)&…...
适用于 Linux、Windows 和 macOS 的免费 ONLYOFFICE 桌面应用程序
前言: 最近也是发现了一款特别好用的免费ONLYOFFICE 桌面应用程序忍不住分享给大家,这款编辑器能够打开、阅读和编辑多种文件类型,包括.docx文档、.pptx幻灯片和.xlsx表格等开放XML格式的Office文档。此外,ONLYOFFICE桌面编辑器还…...

C++面向对象程序设计-北京大学-郭炜【课程笔记(四)】
C面向对象程序设计-北京大学-郭炜【课程笔记(四)】 1、this指针1.1、this指针的作用1.2、this指针和静态成员函数 2、静态成员变量和静态成员函数2.1、基本概念2.2、基本概念总结2.3、如何访问静态成员2.4、静态成员变量的使用场景(重要&…...
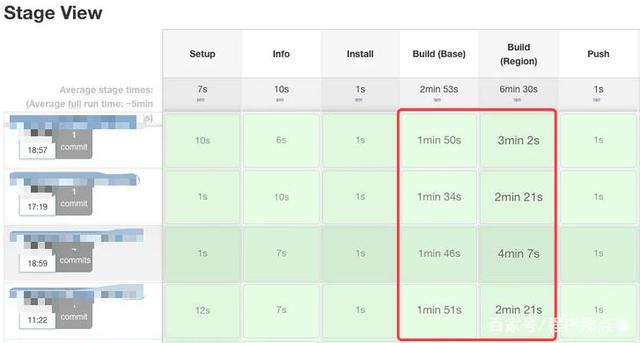
前端构建效率优化之路
项目背景 我们的系统(一个 ToB 的 Web 单页应用)前端单页应用经过多年的迭代,目前已经累积有大几十万行的业务代码,30 路由模块,整体的代码量和复杂度还是比较高的。 项目整体是基于 Vue TypeScirpt,而构…...

react实现拖拽的插件
插件一:dnd-kit 插件官网链接https://docs.dndkit.com/introduction/installation 插件二:react-beautiful-dnd https://github.com/atlassian/react-beautiful-dnd/tree/master 两个插件的区别: 插件一可以做到从区域A拖住到区域B 插件二…...

解决Uncaught SyntaxError: Cannot use import statement outside a module(at XXX)报错
报错原因:这个错误通常是因为你正在尝试在一个不支持 ES6 模块语法的环境中使用 import 语句。这可能是因为你的代码是在一个只支持 CommonJS 或 AMD 模块系统的环境中运行的,或者你的代码运行的环境没有正确配置以支持 ES6 模块。如果是在浏览器环境&am…...

PHP如何利用post与get方式传值接收数据
目录 一、POST传值1. 使用curl库发送 POST 请求:2. 使用file_get_contents()函数发送 POST 请求:3. 使用stream_socket_client()函数发送 POST 请求:4. 利用from表单提交数据: 二、GET传值1. 使用http_build_query()函数构建 URL …...
在Mac上搭建MongoDB环境
最近工作中需要装MongoDB环境,搭建过程中遇到了一些问题,在这里记录一下安装MongoDB环境的方法以及问题的解决方法。有两种安装MongoDB的方法:brew安装和手动安装。 目录 使用Homebrew安装MongoDB 手动安装MongoDB(不使用Homebr…...

第三十九天| 62.不同路径、63. 不同路径 II
Leetcode 62.不同路径 题目链接:62 不同路径 题干:一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “…...

提高代码质量的 10 条编码原则
提高代码质量的 10 条编码原则 本文转自 公众号 ByteByteGo,如有侵权,请联系,立即删除 今天来聊聊提高代码质量的 10 条编码原则。 软件开发需要良好的系统设计和编码标准。我们在下图中列出了 10 条良好的编码原则。 01 遵循代码规范 我们…...

SHERlocked93 的 2017 年终总结
回家的路上有点无聊,简短回顾一下2017年的得失收获 开始两个月3月到5月用C#完结了一个烂尾的wpf小项目,对自己前半年的.net生涯也算是一个句号(虽然不知道最后有没有采用),后面由于项目组转变技术栈,选择了…...
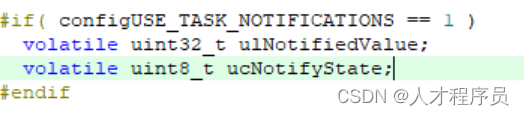
【FreeRTOS基础入门】任务通知
文章目录 前言一、任务通知介绍1.1 任务通知怎么通信1.2 任务通知与其他通信方式的区别1.3 优势及限制任务通知的优势任务通知的限制 1.4 内部原理 二、任务通知的使用2.1 发出与接收通知简化版2.1 发出与接收通知专业版 总结 前言 FreeRTOS 提供了丰富而灵活的任务通知机制&a…...

python opencv比较图片相似度
目录 一:均值哈希算法 二:三直方图算法 三:单通道直方图 一:均值哈希算法 均值哈希算法是一种快速比较图像相似度的方法。它首先将图像转化为灰度图像,然后计算图像的均值,接着将每个像素的...

校园兼职|大学生校园兼职小程序|基于微信小程序的大学生校园兼职系统设计与实现(源码+数据库+文档)
大学生校园兼职小程序目录 目录 基于微信小程序的大学生校园兼职系统设计与实现 一、前言 二、系统功能设计 三、系统实现 1、用户微信端功能模块 2、管理员服务端功能模块 (1) 兼职管理 (2)论坛管理 (3&…...

linux系统离线安装docker服务教程
1、下载、上传docker-20.10.0.tgz压缩包至服务器,其中,docker下载地址https://download.docker.com/linux/static/stable/x86_64/ 2、新建安装docker脚本docker-install.sh #!/usr/bin/env bash tar -xvf docker-20.10.0.tgzcp docker/* /usr/bin/cat …...

【青龙】快速搭建青龙面板,部署属于你自己的应用!
青龙面板是一个支持 Python3、JavaScript、Shell、Typescript 的定时任务管理平台。 废话不多说,直接开始。 这里使用一台 雨云 的云服务器作为演示。雨云注册地址:https://www.rainyun.com/ 优惠码:lz932 使用优惠码注册后绑定微信可获得8折…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...
