第三十九天| 62.不同路径、63. 不同路径 II
Leetcode 62.不同路径
题目链接:62 不同路径
题干:一个机器人位于一个
m x n网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。问总共有多少条不同的路径?
思考一:动态规划。
- 确定dp数组(dp table)以及下标的含义
dp[i][j] :表示从(0 ,0)出发,到(i, j) 有dp[i][j]条不同的路径。
- 确定递推公式
从dp[i][j]的定义可以看出,只能有两个方向来推导出来,即dp[i - 1][j]向右走 和 dp[i][j - 1]向下走。
所以dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。
- dp数组的初始化
首先dp[i][0]一定都是1,因为从(0, 0)的位置到(i, 0)的路径只有一条,dp[0][j]也同理。代码如下:
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
- 确定遍历顺序
从递归公式dp[i][j] = dp[i - 1][j] + dp[i][j - 1];中可以看出,dp[i][j]是依赖 dp[i - 1][j]和 dp[i][j - 1],那么遍历的顺序一定是从左到右一层一层遍历的。
- 举例推导dp数组
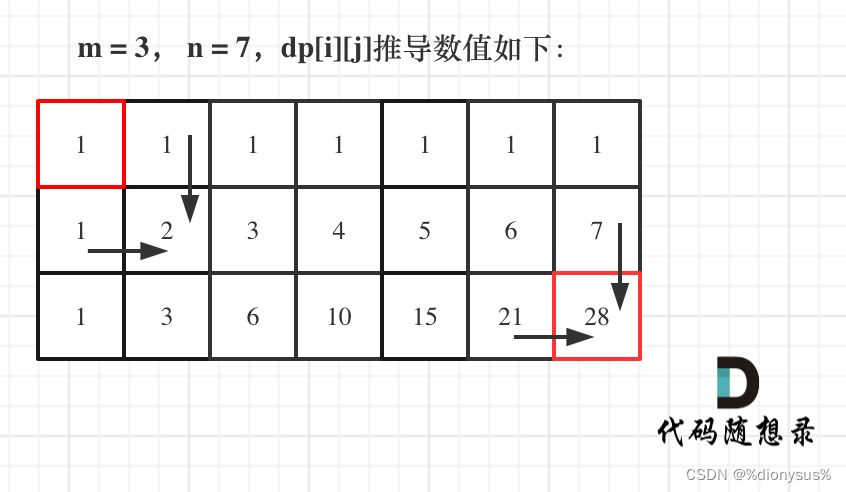
代码:
class Solution {
public:int uniquePaths(int m, int n) {int dp[m][n]; //记录到达下标(i,j)的路径数//初始化for (int i = 0; i < m; i++) //从起始点一直到最右边只存在一条路径dp[i][0] = 1;for (int j = 0; j < n; j++) //从起始点一直到最下边只存在一条路径dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++)dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; //递推公式}return dp[m - 1][n - 1];}
};优化:其实用一个一维数组(可以理解是滚动数组)即可,可以优化空间。
代码:
class Solution {
public:int uniquePaths(int m, int n) {vector<int> dp(n);for (int i = 0; i < n; i++) dp[i] = 1; //初始化for (int j = 1; j < m; j++) {for (int i = 1; i < n; i++) { //处理每列元素dp[i] += dp[i - 1];}}return dp[n - 1];}
};思考二:深度优先搜索。题目中说机器人每次只能向下或者向右移动一步,那么其实机器人走过的路径可以抽象为一棵二叉树,而叶子节点就是终点!如图:

但如果只是按以上思路同一位置多次计算,会超时。因此要加上备忘录,初始化为-1。终止条件加上判断当前位置备忘录是否记录过,记录过则直接返回数据。单层递归处理逻辑也要记录数据。
代码:
class Solution {
public:vector<vector<int>> memo; //添加备忘录int dfs(int row, int col, const int m, const int n) {if (row > m || col > n) return 0; //超出边界返回0if (row == m && col == n) return 1; //搜索到一条路径if (memo[row][col] != -1) return memo[row][col]; //访问过则直接返回记录值int right = dfs(row + 1, col, m, n); //向右移动int down = dfs(row, col + 1, m, n); //向下移动memo[row][col] = right + down; //记录数据return memo[row][col]; }int uniquePaths(int m, int n) {if (m < 1 || n < 1) return 0;memo = vector<vector<int>>(m + 1, vector<int>(n + 1, -1));return dfs(1, 1, m, n);}
};思考三:数论法。
在下图中,可以看出一共m,n的话,无论怎么走,走到终点都需要 m + n - 2 步。

在这m + n - 2 步中,一定有 m - 1 步是要向下走的,不用管什么时候向下走。
那么路径问题就转换为,给你m + n - 2个不同的数,随便取m - 1(或n - 1)个数,有几种取法。
这便是组合问题。答案为或
,取较小值计算。
求组合要防止两个int相乘溢出。 所以不能把算式的分子都算出来,分母都算出来再做除法。
代码:
class Solution {
public:int uniquePaths(int m, int n) {long long numerator = 1; //分子int denominator = 1; //分母int count = m > n ? n - 1 : m - 1;int num = m + n - 2;while (count > 0) { //边乘边除numerator *= num;denominator *= count;if (denominator != 1 && numerator % denominator == 0) { //可整除numerator /= denominator;denominator = 1;}num--;count--;}return numerator;}
};Leetcode 63. 不同路径 II
题目链接:63 不同路径 II
题干:一个机器人位于一个
m x n网格的左上角 (起始点在下图中标记为 “Start” )。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用
1和0来表示。
思考一:动态规划。
和上题的区别仅在障碍物,因此思路仅在确定递推公式和dp数组的初始化两步存在差异
- 确定递推公式
从dp[i][j]的定义可以看出,只能有两个方向来推导出来,即dp[i - 1][j]向右走 和 dp[i][j - 1]向下走。
正常公式应为dp[i][j] = dp[i - 1][j] + dp[i][j - 1]。
但障碍物所在位置不可达,因此在处理前先判断。代码如下:
if (obstacleGrid[i][j] == 1) //此下标位置存在障碍物 continue; - dp数组的初始化
由于障碍物的存在,因此只有在未碰到障碍物的前面位置dp[i][0]=1。dp[0][j]也同理。代码如下:
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) //从起始点向右直到碰到边界或者障碍物只存在一条路径dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) //从起始点向下直到碰到边界或者障碍物只存在一条路径dp[0][j] = 1;代码:
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) //如果在起点或终点出现了障碍直接返回0return 0;vector<vector<int>> dp(m, vector<int>(n, 0)); //记录到达下标(i,j)的路径数 //初始化for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) //从起始点向右直到碰到边界或者障碍物只存在一条路径dp[i][0] = 1;for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) //从起始点向下直到碰到边界或者障碍物只存在一条路径dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 1) continue; //此下标位置存在障碍物dp[i][j] = dp[i - 1][j] + dp[i][j - 1]; //递推公式}}return dp[m - 1][n - 1];}
};思考二:深度优先搜索。仅在终止条件这多加碰到障碍物则此条路径作废返回0即可。当然还得加上备忘录减少处理时间。
代码:
class Solution {
public:vector<vector<int>> memo; //添加备忘录int dfs(int row, int col, const int m, const int n, const vector<vector<int>>& obstacleGrid) {if (row > m - 1 || col > n - 1) return 0; //超出边界返回0if (obstacleGrid[row][col] == 1) return 0; //碰到障碍物返回0if (row == m - 1 && col == n - 1) return 1; //搜索到一条路径if (memo[row][col] != -1) return memo[row][col]; //访问过则直接返回记录值int right = dfs(row + 1, col, m, n, obstacleGrid); //向右int down = dfs(row, col + 1, m, n, obstacleGrid); //向下memo[row][col] = right + down; //记录数据return memo[row][col];}int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();memo = vector<vector<int>>(m, vector<int>(n, -1));if (m < 1 || n < 1) return 0;return dfs(0, 0, m, n, obstacleGrid);}
};自我总结:
- 了解到C++备忘录模式,减少处理时间。
相关文章:

第三十九天| 62.不同路径、63. 不同路径 II
Leetcode 62.不同路径 题目链接:62 不同路径 题干:一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “…...

提高代码质量的 10 条编码原则
提高代码质量的 10 条编码原则 本文转自 公众号 ByteByteGo,如有侵权,请联系,立即删除 今天来聊聊提高代码质量的 10 条编码原则。 软件开发需要良好的系统设计和编码标准。我们在下图中列出了 10 条良好的编码原则。 01 遵循代码规范 我们…...

SHERlocked93 的 2017 年终总结
回家的路上有点无聊,简短回顾一下2017年的得失收获 开始两个月3月到5月用C#完结了一个烂尾的wpf小项目,对自己前半年的.net生涯也算是一个句号(虽然不知道最后有没有采用),后面由于项目组转变技术栈,选择了…...
【FreeRTOS基础入门】任务通知
文章目录 前言一、任务通知介绍1.1 任务通知怎么通信1.2 任务通知与其他通信方式的区别1.3 优势及限制任务通知的优势任务通知的限制 1.4 内部原理 二、任务通知的使用2.1 发出与接收通知简化版2.1 发出与接收通知专业版 总结 前言 FreeRTOS 提供了丰富而灵活的任务通知机制&a…...

python opencv比较图片相似度
目录 一:均值哈希算法 二:三直方图算法 三:单通道直方图 一:均值哈希算法 均值哈希算法是一种快速比较图像相似度的方法。它首先将图像转化为灰度图像,然后计算图像的均值,接着将每个像素的...

校园兼职|大学生校园兼职小程序|基于微信小程序的大学生校园兼职系统设计与实现(源码+数据库+文档)
大学生校园兼职小程序目录 目录 基于微信小程序的大学生校园兼职系统设计与实现 一、前言 二、系统功能设计 三、系统实现 1、用户微信端功能模块 2、管理员服务端功能模块 (1) 兼职管理 (2)论坛管理 (3&…...

linux系统离线安装docker服务教程
1、下载、上传docker-20.10.0.tgz压缩包至服务器,其中,docker下载地址https://download.docker.com/linux/static/stable/x86_64/ 2、新建安装docker脚本docker-install.sh #!/usr/bin/env bash tar -xvf docker-20.10.0.tgzcp docker/* /usr/bin/cat …...

【青龙】快速搭建青龙面板,部署属于你自己的应用!
青龙面板是一个支持 Python3、JavaScript、Shell、Typescript 的定时任务管理平台。 废话不多说,直接开始。 这里使用一台 雨云 的云服务器作为演示。雨云注册地址:https://www.rainyun.com/ 优惠码:lz932 使用优惠码注册后绑定微信可获得8折…...
shell脚本实现Mysql分库分表备份
一.数据库的分库分表? 12张图把分库分表讲的明明白白!阿里面试:我们为什么要分库分表https://mp.weixin.qq.com/s?__bizMzU0OTE4MzYzMw&mid2247547792&idx2&sn91a10823ceab0cb9db26e22783343deb&chksmfbb1b26eccc63b784879…...
)
【算法 - 动态规划】从零开始学动态规划!(总纲)
动态规划 动态规划(Dynamic Programming,DP)是一种优化问题求解方法,通常用于解决具有 重叠子问题 和 最优子结构 性质的问题。它的基本思想是将原问题分解成更小的子问题,通过求解和保存这些子问题的解,避…...
从 Elasticsearch 到 Apache Doris,统一日志检索与报表分析,360 企业安全浏览器的数据架构升级实践
导读:随着 360 企业安全浏览器用户规模的不断扩张,浏览器短时间内会产生大量的日志数据。为了提供更好的日志数据服务,360 企业安全浏览器设计了统一运维管理平台,并引入 Apache Doris 替代了 Elasticsearch,实现日志检…...

【力扣 - 二叉树的直径】
题目描述 给你一棵二叉树的根节点,返回该树的 直径 。 二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。 两节点之间路径的 长度 由它们之间边数表示。 提示: 树中节点数目在范围 [1, 10000] 内…...
大数据,对于生活的改变
谷歌通过对于疾病的查询量可以预测一个个h1n1病毒的大爆发, 大数据时代对于人的考验 用户的搜索记录就是一种信息,这种信息会满足其基础相关的词条与其有关的词条(最为原始的搜索机制,国内的搜索引擎都是采用这种基础原理。&…...

py2neo和neo4j
py2neo 和 neo4j 是两个 Python 中与 Neo4j 图数据库交互的库,但它们有不同的设计和使用方式。 py2neo: 类型: py2neo 是一个面向对象的库,提供了一个对象模型,使得与 Neo4j 数据库的交互更加 Pythonic。API 风格: 使用 Node 和 Relationship…...

解决windows无法访问wsl下docker服务
笔者在初学使用wsl跑docker时,遇到了windows无法访问的问题,并且浏览了大部分的文章,发现并没有起效,在反复试错终于成功之后,总结为以下几点: 1.升级至wsl2 2.将.wslconfig文件(用户文件夹下)中的如下镜像服务关闭删除 networkingModemirrored 3.打开wsl防火墙相应的端口 …...
OpenAI划时代大模型——文本生成视频模型Sora作品欣赏(二)
Sora介绍 Sora是一个能以文本描述生成视频的人工智能模型,由美国人工智能研究机构OpenAI开发。 Sora这一名称源于日文“空”(そら sora),即天空之意,以示其无限的创造潜力。其背后的技术是在OpenAI的文本到图像生成模…...
Python第十九章(模块)
系统的模块库一般处于外部库中的Lib里面 一。导入模块的方式: 1.方式一: 导入:import 模块名1,模块名2 调用:模块名 . 功能名() 2.方式二: 导入:from 模块名 import 功能1,功能…...
【Linux网络编程五】Tcp套接字编程(四个版本服务器编写)
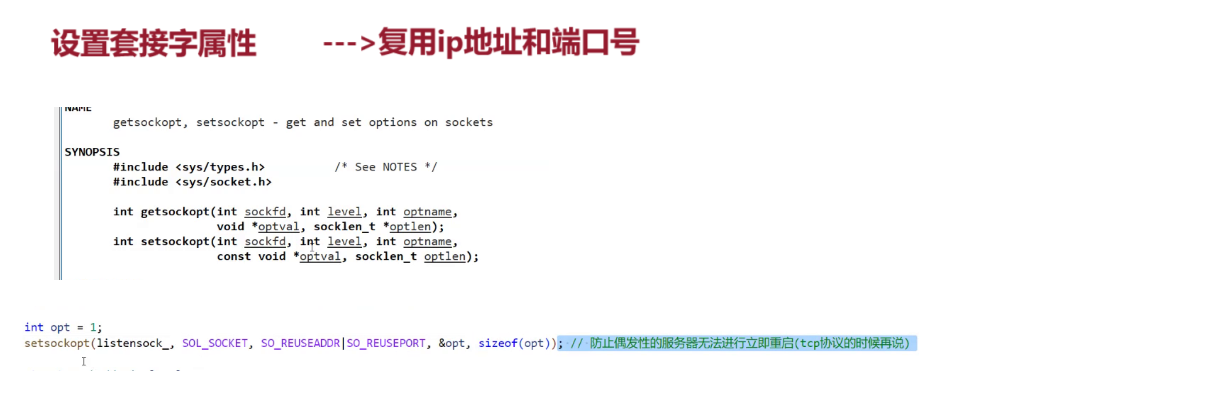
【Linux网络编程五】Tcp套接字编程(四个版本服务器编写) [Tcp套接字编程]一.服务器端进程:1.创建套接字2.绑定网络信息3.设置监听状态4.获取新连接5.根据新连接进行通信 二.客户端进程:1.创建套接字2.连接服务器套接字3.连接成功后进行通信 三…...

APP 有漏洞被测要下架,怎么处理?
事情的经过是这样的: 1:学员公司测试的 APP 发现有漏洞,被要求下架 2:他被公司要求去查询 APP 哪里有漏洞 3:他来寻求帮助,推荐几款安全测试扫描漏洞的问题。 事情的梳理: 1:我们看了他的 …...
)
2024年2月19日-2月25日(全面进行+收集免费虚幻商城资源)
试试周一到周五重点进行,周末抄写源码,周一晚上看书很快就在22:00睡着,早上可以看看视频教程,出租车上补觉。 执行如下: 周一: 8:01-9:20ue4 rpg(184…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

