【算法 - 动态规划】从零开始学动态规划!(总纲)
动态规划
动态规划(Dynamic Programming,DP)是一种优化问题求解方法,通常用于解决具有 重叠子问题 和 最优子结构 性质的问题。它的基本思想是将原问题分解成更小的子问题,通过求解和保存这些子问题的解,避免重复计算,从而提高算法的效率。
基本概念:
-
最优子结构:
- 最优子结构是指问题的最优解可以通过
子问题的最优解递归构建而成。在动态规划中,原问题被分解为更小的子问题,每个子问题都有自己的最优解。通过合并这些最优解,我们可以得到整体问题的最优解。
- 最优子结构是指问题的最优解可以通过
-
重叠子问题:
- 动态规划问题会涉及到重叠子问题,即在解问题的过程中会多次遇到
相同的子问题。为了避免重复计算,动态规划使用记忆化或者其他方法来保存子问题的解。
- 动态规划问题会涉及到重叠子问题,即在解问题的过程中会多次遇到
-
状态转移方程:
- 状态转移方程是问题建模的关键,它描述了问题的
当前状态和如何从之前的状态转移到新状态。通过定义合适的状态和状态之间的转移关系,可以得到问题的递推解法,将子问题和整体连接了起来。
- 状态转移方程是问题建模的关键,它描述了问题的
-
存储中间结果:
- 为了避免重复计算,动态规划通常使用数组、矩阵或字典等数据结构来
存储中间结果。这些中间结果包括子问题的解,可以在需要时直接获取,而不必重新计算。
- 为了避免重复计算,动态规划通常使用数组、矩阵或字典等数据结构来
-
自底向上或自顶向下的求解方法:
- 动态规划可以采用
自底向上(Bottom Up)或自顶向下(Top Down)的求解方法。自底向上是从最小的子问题开始逐步求解,而自顶向下是通过递归从原始问题开始,逐步分解为子问题。
- 动态规划可以采用
这几个基本概念通常共同作用,构成了动态规划算法的基础。具体步骤包括:
定义状态: 确定问题的状态,即问题的子结构和需要求解的变量。
找到状态转移方程: 建立子问题之间的递推关系,通过状态之间的转移来描述问题的求解过程。
初始化边界条件: 将最小的子问题的解设置为初始条件,为递推提供基础。
自底向上或自顶向下求解: 使用 迭代(
自底向上)或 递归(自顶向下)的方法,按照状态转移方程求解子问题,最终得到整体问题的解。
适用场景
动态规划广泛应用于解决各种问题,例如 最短路径问题、背包问题、编辑距离 等。通过合理建模问题,定义好 状态 和 状态转移方程 ,就能够高效地解决复杂的优化问题。
看完以上内容,是不是在遇到一道 动态规划 的题目仍然不知道如何思考,从哪开始着手写?
答案是:从递归开始!
暴力递归
-
基本思想:
- 是一种很朴素的解决问题的方法,通过递归考察所有可能的解决方案来找到办法。有明确的不需要继续递归的条件,即
base case。
- 是一种很朴素的解决问题的方法,通过递归考察所有可能的解决方案来找到办法。有明确的不需要继续递归的条件,即
-
重复计算问题:
- 暴力递归通常不会对重复的子问题进行记忆,可能会导致相同子问题
重复计算。
- 暴力递归通常不会对重复的子问题进行记忆,可能会导致相同子问题
-
时间复杂度问题:
- 由于暴力递归会考虑所有可能的组合,可能会导致
指数级的时间复杂度。
- 由于暴力递归会考虑所有可能的组合,可能会导致
-
适用情况:
- 当问题
规模较小且可能的解决方案数量有限时,暴力递归可能表现的很有效。
- 当问题
要想写出递归函数,要明确以下几点:
1. 定义 Base Case :
- 递归函数应该有一个或多个基本情况,即不再递归调用的情况。
- 基本情况通常是问题可以直接解决的最小子问题。
2. 定义状态
- 状态是问题的变量,用于描述问题的不同方面,应该包含问题的所有相关信息。
3. 定义递归函数的功能
- 只有明确了递归函数的功能,才能知道需要哪些状态变量。
- 同时也明确了主函数调用时,如何传递初始参数。
因此,要想写出动态规划,大体步骤就是:
思考题目如何用最最普通的思路写出递归函数
画图,寻找哪些地方会存在可以优化的点
保存部分或全部状态,避免重复计算
接下来的 系列文章 会带大家一步一步的从 暴力递归 优化出 动态规划 ,并深入理解动态规划的基本概念以及书写步骤!
敬请期待一下吧 ~
相关文章:
)
【算法 - 动态规划】从零开始学动态规划!(总纲)
动态规划 动态规划(Dynamic Programming,DP)是一种优化问题求解方法,通常用于解决具有 重叠子问题 和 最优子结构 性质的问题。它的基本思想是将原问题分解成更小的子问题,通过求解和保存这些子问题的解,避…...
从 Elasticsearch 到 Apache Doris,统一日志检索与报表分析,360 企业安全浏览器的数据架构升级实践
导读:随着 360 企业安全浏览器用户规模的不断扩张,浏览器短时间内会产生大量的日志数据。为了提供更好的日志数据服务,360 企业安全浏览器设计了统一运维管理平台,并引入 Apache Doris 替代了 Elasticsearch,实现日志检…...

【力扣 - 二叉树的直径】
题目描述 给你一棵二叉树的根节点,返回该树的 直径 。 二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。 两节点之间路径的 长度 由它们之间边数表示。 提示: 树中节点数目在范围 [1, 10000] 内…...
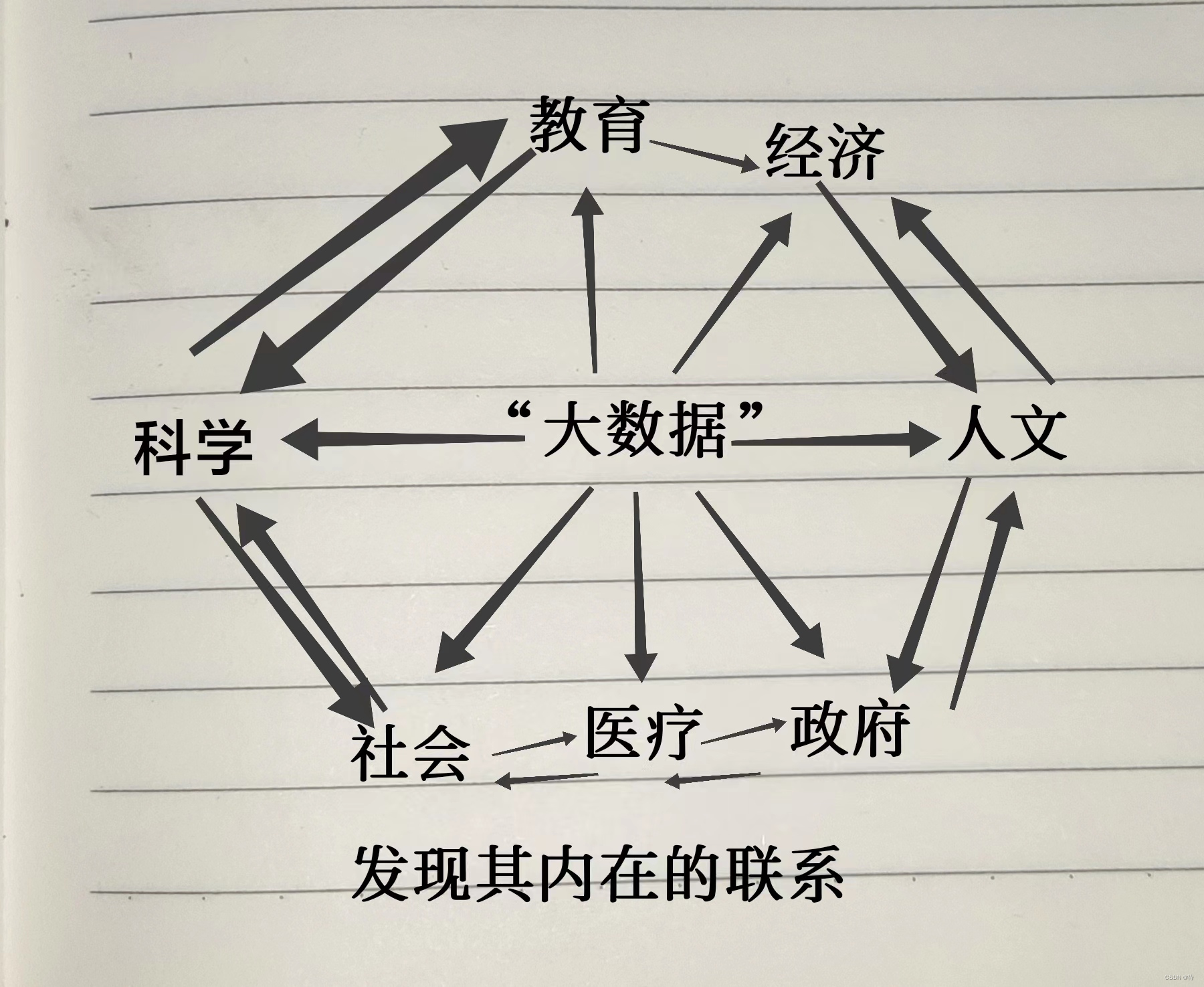
大数据,对于生活的改变
谷歌通过对于疾病的查询量可以预测一个个h1n1病毒的大爆发, 大数据时代对于人的考验 用户的搜索记录就是一种信息,这种信息会满足其基础相关的词条与其有关的词条(最为原始的搜索机制,国内的搜索引擎都是采用这种基础原理。&…...

py2neo和neo4j
py2neo 和 neo4j 是两个 Python 中与 Neo4j 图数据库交互的库,但它们有不同的设计和使用方式。 py2neo: 类型: py2neo 是一个面向对象的库,提供了一个对象模型,使得与 Neo4j 数据库的交互更加 Pythonic。API 风格: 使用 Node 和 Relationship…...

解决windows无法访问wsl下docker服务
笔者在初学使用wsl跑docker时,遇到了windows无法访问的问题,并且浏览了大部分的文章,发现并没有起效,在反复试错终于成功之后,总结为以下几点: 1.升级至wsl2 2.将.wslconfig文件(用户文件夹下)中的如下镜像服务关闭删除 networkingModemirrored 3.打开wsl防火墙相应的端口 …...
OpenAI划时代大模型——文本生成视频模型Sora作品欣赏(二)
Sora介绍 Sora是一个能以文本描述生成视频的人工智能模型,由美国人工智能研究机构OpenAI开发。 Sora这一名称源于日文“空”(そら sora),即天空之意,以示其无限的创造潜力。其背后的技术是在OpenAI的文本到图像生成模…...
Python第十九章(模块)
系统的模块库一般处于外部库中的Lib里面 一。导入模块的方式: 1.方式一: 导入:import 模块名1,模块名2 调用:模块名 . 功能名() 2.方式二: 导入:from 模块名 import 功能1,功能…...
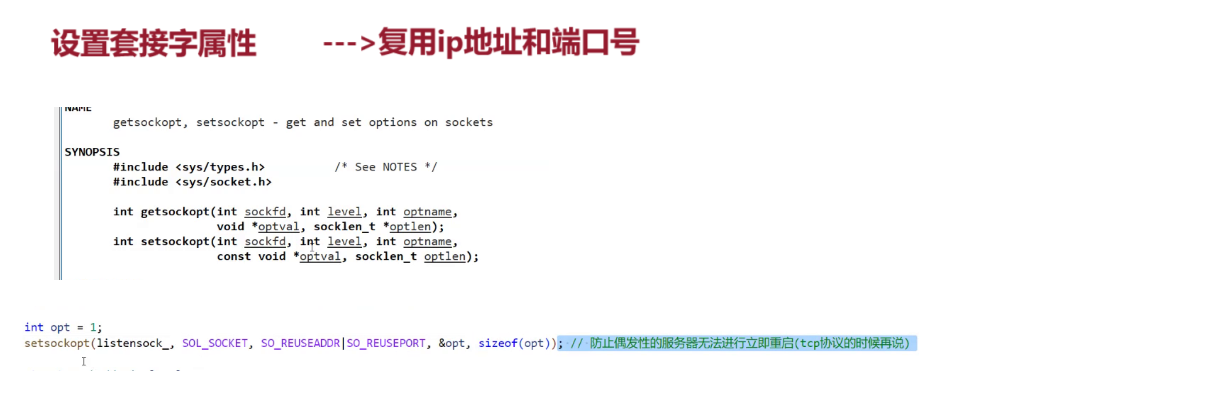
【Linux网络编程五】Tcp套接字编程(四个版本服务器编写)
【Linux网络编程五】Tcp套接字编程(四个版本服务器编写) [Tcp套接字编程]一.服务器端进程:1.创建套接字2.绑定网络信息3.设置监听状态4.获取新连接5.根据新连接进行通信 二.客户端进程:1.创建套接字2.连接服务器套接字3.连接成功后进行通信 三…...

APP 有漏洞被测要下架,怎么处理?
事情的经过是这样的: 1:学员公司测试的 APP 发现有漏洞,被要求下架 2:他被公司要求去查询 APP 哪里有漏洞 3:他来寻求帮助,推荐几款安全测试扫描漏洞的问题。 事情的梳理: 1:我们看了他的 …...
)
2024年2月19日-2月25日(全面进行+收集免费虚幻商城资源)
试试周一到周五重点进行,周末抄写源码,周一晚上看书很快就在22:00睡着,早上可以看看视频教程,出租车上补觉。 执行如下: 周一: 8:01-9:20ue4 rpg(184…...
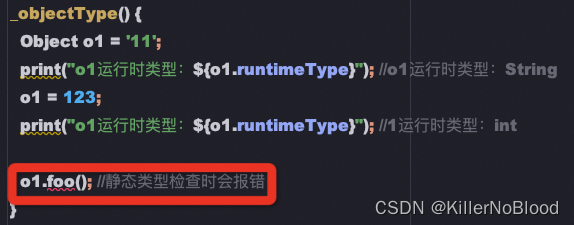
Flutter学习4 - Dart数据类型
1、基本数据类型 num、int、double (1)常用数据类型 num类型,是数字类型的父类型,有两个子类 int 和 double 通过在函数名前加下划线,可以将函数变成私有函数,私有函数只能在当前文件中调用 //常用数据…...

leetcode hot100单词拆分
在本题中,我们是要把一个字符串,判断是否能用给的字符串数组中的单词进行拆分,如果可以则返回true,不能的话则返回false。这个题一开始看无法与背包问题联系在一起。但仔细考虑,就是用物品(给的字符串数组中…...
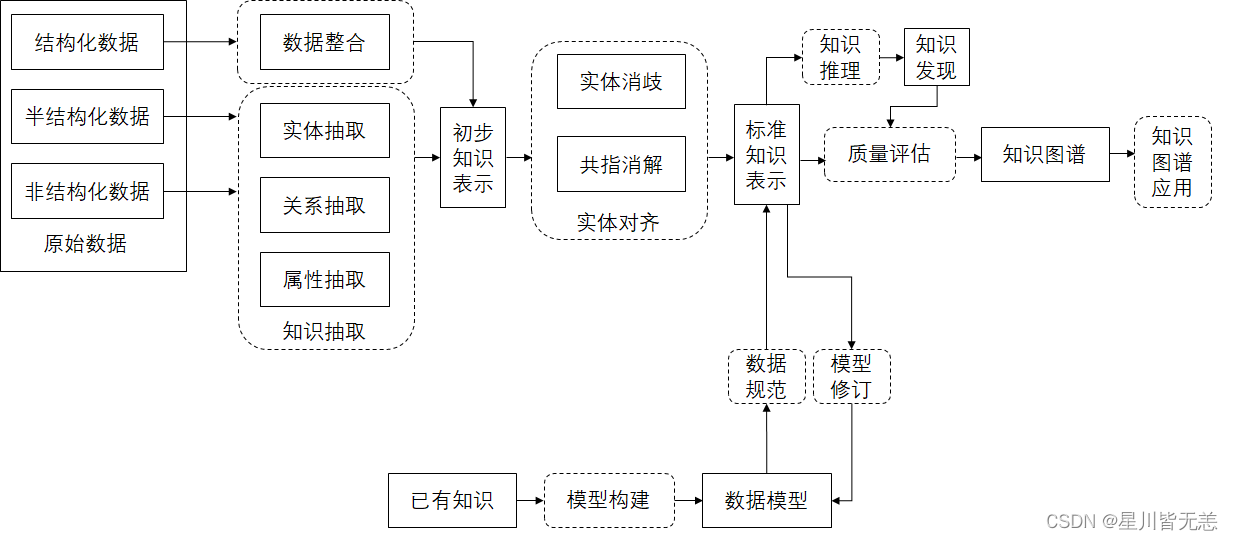
大数据构建知识图谱:从技术到实战的完整指南
文章目录 大数据构建知识图谱:从技术到实战的完整指南一、概述二、知识图谱的基础理论定义与分类核心组成历史与发展 三、知识获取与预处理数据源选择数据清洗实体识别 四、知识表示方法知识表示模型RDFOWL属性图模型 本体构建关系提取与表示 五、知识图谱构建技术图…...
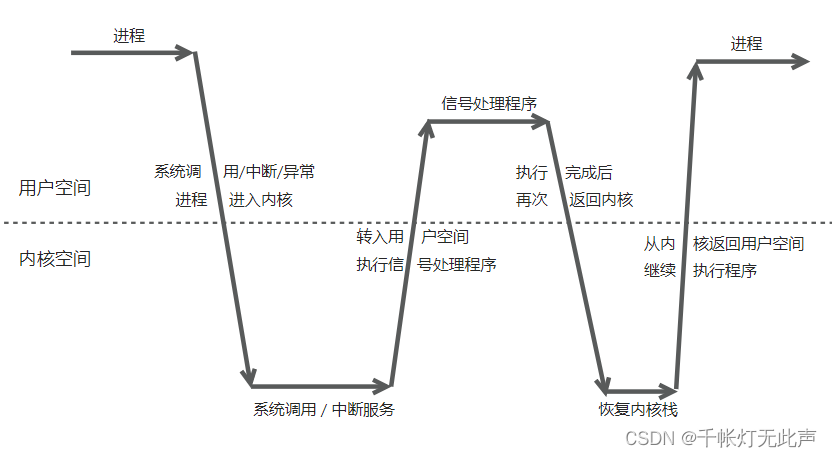
WebServer -- 定时器处理非活动连接(上)
目录 🍍函数指针 🌼基础知识 🐙整体概述 🎂基础API sigaction 结构体 sigaction() sigfillset() SIGALRM, SIGTERM 信号 alarm() socketpair() send() 📕信号通知流程 统一事件源 信号处理机制 &#x…...

微服务部署:金丝雀发布、蓝绿发布和滚动发布的对比
金丝雀发布、蓝绿发布和滚动发布的对比 金丝雀发布、蓝绿发布和滚动发布都是软件发布策略,它们都旨在降低发布风险并提高发布速度。但是,这三种策略在工作方式、优缺点等方面存在一些差异。 工作方式 金丝雀发布:将新版本软件逐步发布给用…...
)
轻松入门MySQL:优化复杂查询,使用临时表简化数据库查询流程(13)
在进销存管理系统中,复杂的数据查询是司空见惯的。这些查询往往需要处理大量的数据,并执行复杂的逻辑操作。然而,处理这些查询可能会变得非常耗时,并且难以维护。为了解决这个问题,我们可以利用临时表,这是…...

vmware的ubuntu虚拟机因空间满无法启动
正在虚拟机编译android源代码,没注意空间不足,结果回来发现了 Assuming drive cache: write through 的问题,经查是空间不足的原因 按照这个教程,清除出来部分空间,才能进去系统,并且对系统空间做下优化 …...
Unity数据持久化之PlayerPrefs
这里写目录标题 PlayerPrefs概述基本方法PlayerPrefs存储位置实践小项目反射知识补充数据管理类的创建反射存储数据----常用成员反射存储数据----List成员反射存储数据----Dictionary成员反射存储数据----自定义类成员反射读取数据----常用成员反射读取数据----List成员反射读取…...

uniapp微信公众号H5分享
如果项目文件node_modules中没有weixin-js-sdk文件,则直接使用本文章提供的; 如果不生效,则在template.h5.html中引入 <script src"https://res.wx.qq.com/open/js/jweixin-1.6.0.js"></script> 首先引入weixin-js-…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
