概率基础——几何分布
概率基础——几何分布
介绍
在统计学中,几何分布是描述了在一系列独立同分布的伯努利试验中,第一次成功所需的试验次数的概率分布。在连续抛掷硬币的试验中,每次抛掷结果为正面向上的概率为 p p p,反面向上的概率为 1 − p 1-p 1−p。几何随机变量 X X X表示连续抛掷硬币直到第一次出现正面向上的试验次数。
理论及公式
几何分布的概率质量函数(PMF)为:
P ( X = k ) = ( 1 − p ) k − 1 × p P(X = k) = (1 - p)^{k-1} \times p P(X=k)=(1−p)k−1×p
其中, k k k是试验次数, p p p 是每次试验成功(正面向上)的概率。
几何分布的期望和方差可以通过其概率质量函数得到。设几何随机变量为 X X X,表示第一次成功所需的试验次数。
- 期望(均值):
E ( X ) = 1 p E(X) = \frac{1}{p} E(X)=p1
- 方差:
V a r ( X ) = 1 − p p 2 Var(X) = \frac{1-p}{p^2} Var(X)=p21−p
其中, p p p是每次试验成功(正面向上)的概率。
这些公式可以帮助我们计算几何分布的期望和方差,从而更好地理解该分布的特征和性质。
示例与绘图
接下来,我们将使用Python来实现绘制几何分布的概率质量函数图。
import matplotlib.pyplot as plt
from scipy.stats import geomfig, ax = plt.subplots(2, 1)
params = [0.5, 0.3]x = range(1, 11)for i in range(len(params)):geom_rv = geom(params[i])ax[i].plot(x, geom_rv.pmf(x), 'ro', lw=5, alpha=0.6, label='Geometric PMF')ax[i].vlines(x, 0, geom_rv.pmf(x), colors='r')ax[i].set_xlim(0, 10)ax[i].set_ylim(0, 0.6)ax[i].set_title('p = %.2f' % params[i])ax[i].set_xticks(x)ax[i].set_yticks([0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6])ax[i].grid(ls='--')
plt.show()
运行以上代码,将会得到一个几何分布的概率质量函数图。从图中可以看出,随着试验次数的增加,成功的概率逐渐减小,但总体上呈指数下降的趋势。这是因为每次试验成功的概率 p p p乘以 ( 1 − p ) k − 1 (1-p)^{k-1} (1−p)k−1,随着 k k k的增加, ( 1 − p ) k − 1 (1-p)^{k-1} (1−p)k−1的值逐渐减小,从而导致整体概率下降。
from scipy.stats import geom
import matplotlib.pyplot as pltx = range(1, 20)
geom_rv = geom(p=0.5)
geom_rvs = geom_rv.rvs(size=100000)
plt.hist(geom_rvs, bins=20, density=True, alpha=0.75, edgecolor='black')
plt.gca().axes.set_xticks(range(1, 20))mean, var, skew, kurt = geom_rv.stats(moments='mvsk')
print("Mean:", mean)
print("Variance:", var)
plt.grid(ls='--')
plt.show()

总结
本文介绍了几何分布及Python实现,利用了函数包的各个方法计算出各个理论统计值,利用采样样本数据计算出来的值和理论值基本算都是相等的。
相关文章:

概率基础——几何分布
概率基础——几何分布 介绍 在统计学中,几何分布是描述了在一系列独立同分布的伯努利试验中,第一次成功所需的试验次数的概率分布。在连续抛掷硬币的试验中,每次抛掷结果为正面向上的概率为 p p p,反面向上的概率为 1 − p 1-p …...

JavaScript的内存管理与垃圾回收
前言 JavaScript提供了高效的内存管理机制,它的垃圾回收功能是自动的。在我们创建新对象、函数、原始类型和变量时,所有这些编程元素都会占用内存。那么JavaScript是如何管理这些元素并在它们不再使用时清理它们的呢? 在本节中,…...
Neo4j导入数据之JAVA JDBC
目录结构 前言设置neo4j外部访问代码整理maven 依赖java 代码 参考链接 前言 公司需要获取neo4j数据库内容进行数据筛查,neo4j数据库咱也是头一次基础,辛辛苦苦安装好整理了安装neo4j的步骤,如今又遇到数据不知道怎么创建,关关难…...

LeetCode 2878.获取DataFrame的大小
DataFrame players: ------------------- | Column Name | Type | ------------------- | player_id | int | | name | object | | age | int | | position | object | | … | … | ------------------- 编写一个解决方案,计算并显示 players 的 行数和列数。 将结…...

索引失效的 12 种情况
目录 一、未使用索引字段进行查询 二、索引列使用了函数或表达式 三、使用了不等于(! 或 <>)操作符 四、LIKE 操作符的模糊查询 五、对索引列进行了数据类型转换 六、使用 OR 连接多个条件 七、表中数据量较少 八、索引列上存在大量重复值…...

Spring及工厂模式概述
文章目录 Spring 身世什么是 Spring什么是设计模式工厂设计模式什么是工厂设计模式简单的工厂设计模式通用的工厂设计 总结 在 Spring 框架出现之前,Java 开发者使用的主要是传统的 Java EE(Java Enterprise Edition)平台。Java EE 是一套用于…...

运维SRE-19 网站Web中间件服务-http-nginx
Ans自动化流程 1.网站集群核心协议:HTTP 1.1概述 web服务:网站服务,网站协议即可. 协议:http协议,https协议 服务:Nginx服务,Tengine服务....1.2 HTTP协议 http超文本传输协议,负责数据在网站…...
类型)
C语言—自定义(构造)类型
2.20,17.56 1.只有当我们使用结构体类型定义变量/结构体数组,系统才会为结构体的成员分配内存空间,用于存储对应类型的数据 2.strct 结构体 一起作为结构体类型标识符 嘿嘿暂时先这样,我会回来改的1、定义一个表示公交线路的结构体,要…...
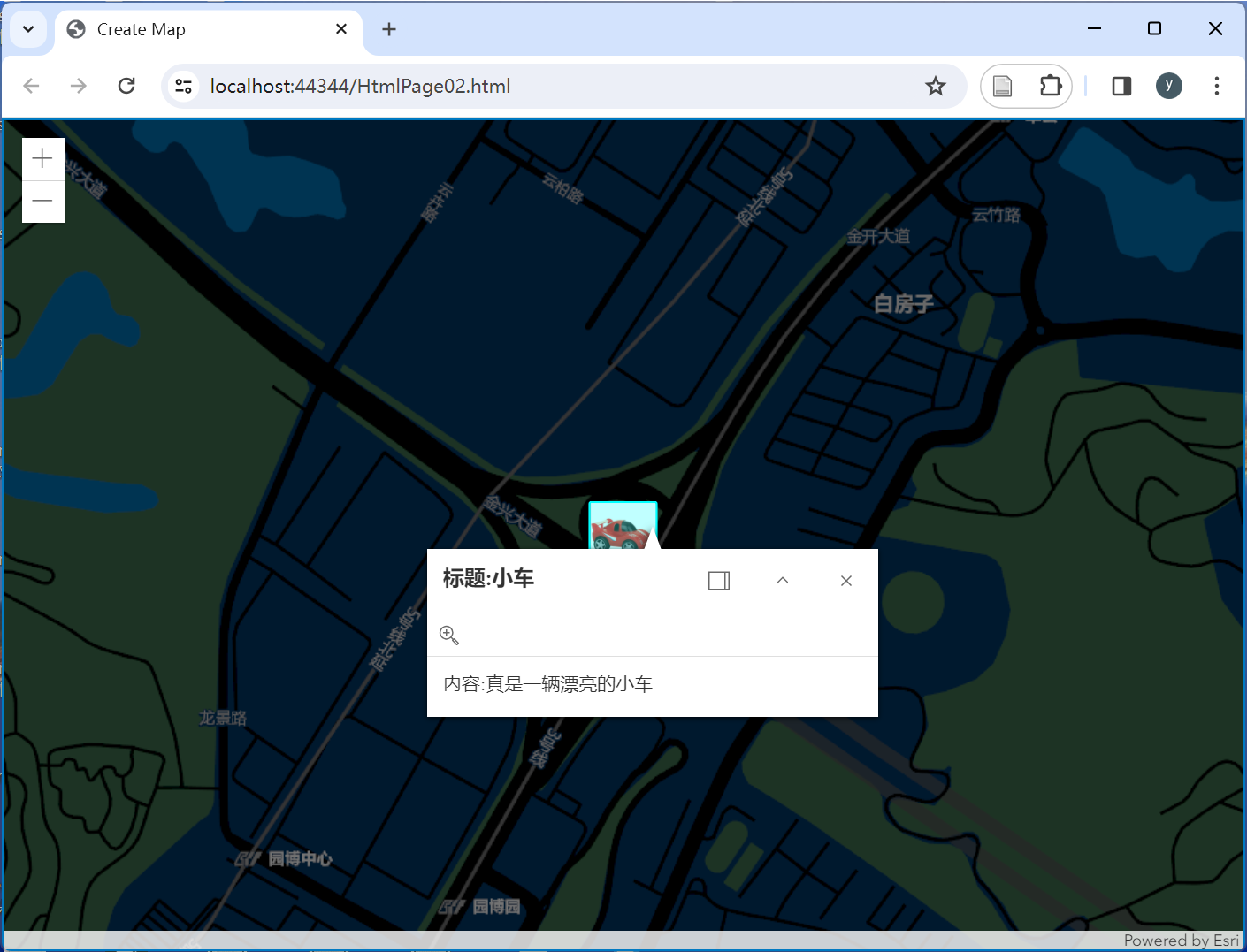
ArcgisForJS如何实现添加含图片样式的点要素?
文章目录 0.引言1.加载底图2.获取点要素的坐标3.添加含图片样式的几何要素4.完整实现 0.引言 ArcGIS API for JavaScript 是一个用于在Web和移动应用程序中创建交互式地图和地理空间分析应用的库。本文在ArcGIS For JavaScript中使用Graphic对象来创建包含图片样式的点要素。 …...
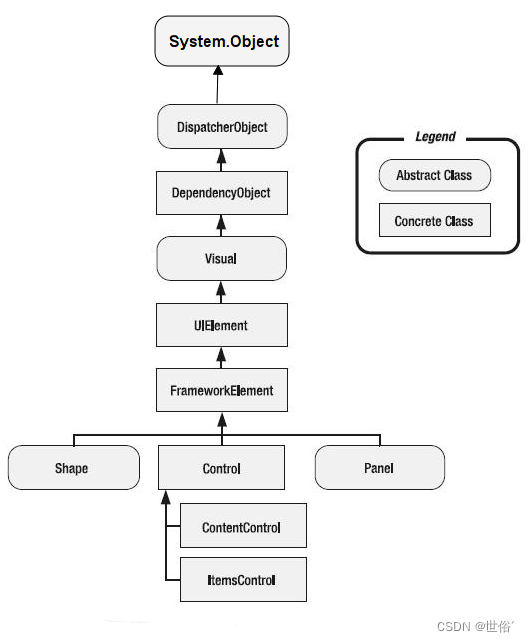
C#之WPF学习之路(2)
目录 控件的父类 DispatcherObject类 DependencyObject类 DependencyObject 类的关键成员和方法 Visual类 Visual 类的主要成员和方法 UIElement类 UIElement 类的主要成员和功能 FrameworkElement类 FrameworkElement 类的主要成员和功能 控件的父类 在 WPF (Windo…...
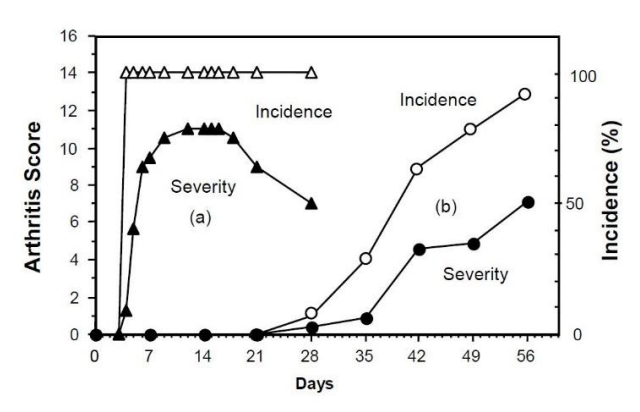
胶原抗体诱导小鼠关节炎模型
胶原诱导性关节炎小鼠(CIA)作为人类类风湿关节炎模型应用广泛,但CIA引起的关节炎起病比较缓慢,造模周期较长,一般为6-8周(1-12)。Chondrex公司已开发出单一种单克隆抗体合剂诱导的小鼠关节炎模型(CAIA),明显缩短了造模…...

集百家所长的开放世界游戏,艾尔莎H311-PRO带你玩转《幻兽帕鲁》
随着近几年开放世界游戏热潮的兴起,如今这类游戏可以说是像雨后春笋般不断推出,比如《幻兽帕鲁》就是近期非常火热的一个代表,它不仅集合了生存、建造、宠物养成等多种元素,而且可爱的卡通画风格更是老少皆宜。那么,这…...
机器人内部传感器阅读笔记及心得-位置传感器-旋转变压器、激光干涉式编码器
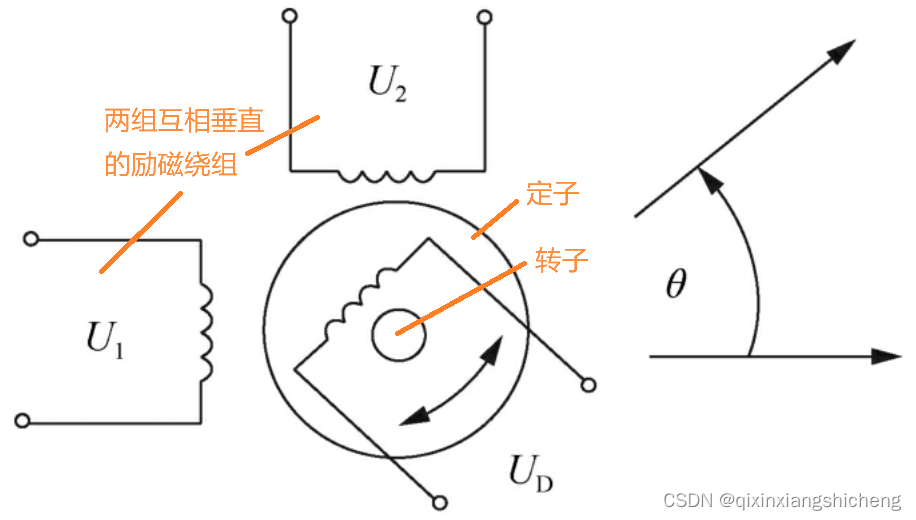
旋转变压器 旋转变压器是一种输出电压随转角变化的检测装置,是用来检测角位移的,其基本结构与交流绕线式异步电动机相似,由定子和转子组成。 旋转变压器的原理如图1所示,定子相当于变压器的一次侧,有两组在空间位置上…...

深度学习的学习笔记帖子2
人脸数据集的介绍: https://zhuanlan.zhihu.com/p/362356480 https://blog.csdn.net/bjbz_cxy/article/details/122210641 CASIAWebFace人脸数据集等的github: https://github.com/deepinsight/insightface/blob/master/recognition/datasets/README.md…...

【机器学习学习脉络】
机器学习学习脉络 基础知识 数学基础 线性代数概率论与数理统计微积分最优化理论 编程基础 Python编程语言数据结构与算法软件工程原则 计算机科学基础 操作系统网络通信数据库系统 机器学习概论 定义与发展历程机器学习的主要任务和应用领域基本术语和概念 监督学习 线…...

golang命令行工具gtcli,实现了完美集成与结构化的gin脚手架,gin-restful-api开箱即用
关于gtools golang非常奈斯,gin作为web框架也非常奈斯,但我们在开发过程中,前期搭建会花费大量的时间,且还不尽人意。 为此我集成了gin-restful-api的模板gin-layout,还有脚手架一键生成项目。 集成相关 ginviperz…...

Qt 事件
1. 事件 事件是对各种应用程序需要知道的由应用程序内部或者外部产生的事情或者动作的通称。在Qt中使用一个对象来表示一个事件,它继承自QEvent类。 2. 事件和信号 事件与信号并不相同,比如我们使用鼠标点击了一下界面上的按钮,那么就会产生…...
JAVA高并发——并行算法
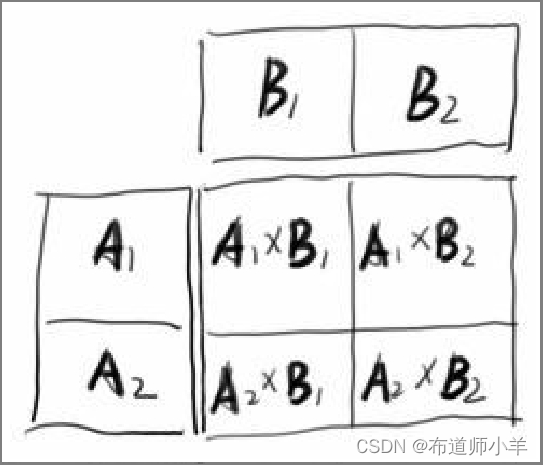
文章目录 1、并行流水线2、并行搜索3、并行排序3.1、分离数据相关性:奇偶交换排序3.2、改进的插入排序:希尔排序 4、并行算法:矩阵乘法 1、并行流水线 并行算法虽然可以充分发挥多核CPU的性能,但并非所有的运算都可以改造成并行的…...
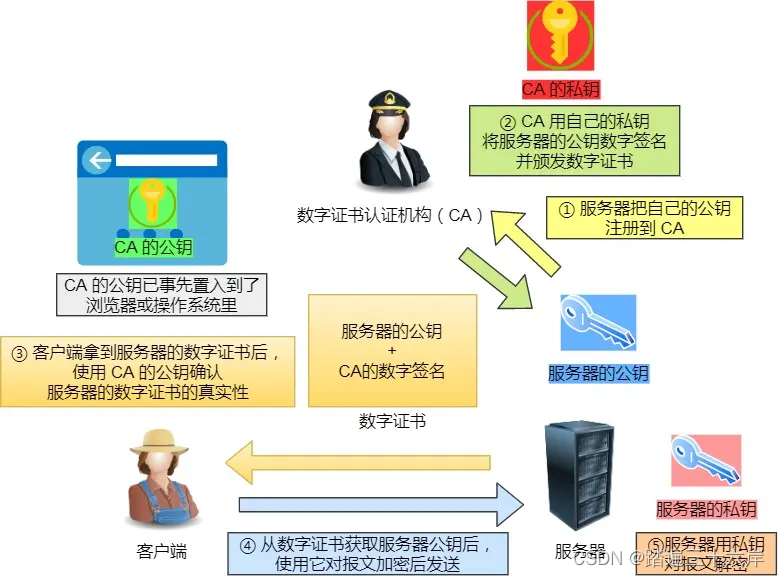
HTTP 与 HTTPS-HTTP 解决了 HTTP 哪些问题?
资料来源 : 小林coding 小林官方网站 : 小林coding (xiaolincoding.com) HTTP 解决了 HTTP 哪些问题? HTTP 由于是明文传输,所以安全上存在以下三个风险: 窃听风险,比如通信链路上可以获取通信内容,用户号容易没。篡改风险,比如…...

S32 Design Studio PE工具配置TMR
配置步骤 配置内容 生成的配置结构体如下,在Generated_Code路径下的lpTmr.c文件和lpTmr.h文件。 /*! lpTmr1 configuration structure */ const lptmr_config_t lpTmr1_config0 {.workMode LPTMR_WORKMODE_PULSECOUNTER,.dmaRequest false,.interruptEnable tr…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...
