最优传输(Optimal Transport)
最优传输(Optimal Transport)是一种数学理论和计算方法,用于描述两个概率分布之间的距离或者对应关系。它的核心概念是如何以最佳方式将一组资源(如质量、能量等)从一个位置传输到另一个位置。
基本概念:
-
概率分布: 在最优传输中,通常涉及到两个概率分布。这些概率分布可以代表不同位置上的资源分布情况,如图像的像素分布、文本中的词语分布等。
-
距离度量: 最优传输理论通过某种距离度量来衡量两个概率分布之间的相似度或差异性。常用的距离度量包括 Wasserstein 距离、Kullback-Leibler 散度等。
-
传输方案: 最优传输问题的目标是找到最佳的资源传输方案,以最小化资源传输的成本。这个传输方案描述了如何将资源从一个分布移动到另一个分布,使得总成本最小化。
数学形式:
在数学上,最优传输问题可以形式化为一个线性规划问题或者凸优化问题,其基本形式如下:
给定两个概率分布 ( ) 和 (
),以及一个成本函数 (
),其中 (
) 表示来自 (
) 的资源,(
) 表示来自 (
) 的资源。最优传输问题可以表述为:
其中 ( ) 是 (
) 和 (
) 之间的联合分布,满足以下条件:
- (
) 的边缘分布分别为 (
) 和 (
)。
- (
) 是可行的传输方案。
应用:
最优传输理论在各个领域都有广泛的应用,包括但不限于:
- 图像处理: 用于图像对齐、图像变形、颜色迁移等任务。
- 机器学习: 用于领域自适应、分布匹配等。
- 经济学: 用于描述供需关系、经济资源配置等。
- 统计学: 用于测量两个随机变量之间的相似度或距离。
一个典型的最优传输问题是在图像处理领域中的图像变形任务。假设有两张图像 A 和 B,我们希望通过最优传输方法将图像 A 中的像素分布转换为图像 B 中的像素分布,以实现图像的变形。
在这个问题中,我们可以将图像 A 和 B 中的像素分布分别视为两个概率分布 ( ) 和 (
)。假设 (
) 和 (
) 分别表示图像 A 和 B 中的像素分布,那么最优传输问题可以表述为:
其中 ( ) 是像素 (
) 和像素 (
) 之间的成本函数,通常是像素之间的距离或者差异度。(
) 是 (
) 和 (
) 之间的联合分布,满足以下条件:
- (
) 的边缘分布分别为 (
) 和 (
)。
- (
) 是可行的传输方案。
解决这个问题的方法通常是通过线性规划或者凸优化方法。一旦找到了最优的传输方案 ( ),我们就可以将图像 A 中的像素按照这个方案重新分布到图像 B 中,从而实现图像的变形。
实例
实例1
一个具体的实例是在图像生成和变换任务中的应用。
假设我们有两幅图像,分别是一张狗的图像和一张猫的图像。我们希望将狗的图像转换成猫的图像,但是这两张图像的风格、颜色、形状等特征可能存在一定的差异。
通过最优传输理论,我们可以量化这两张图像之间的差异,并且找到最佳的映射关系,从而实现图像的转换。具体来说,我们可以将每张图像看作一个概率分布,其中每个像素的灰度值可以看作是一个随机变量。然后,通过计算两个图像之间的Wasserstein距离,我们可以找到将一个图像中的像素映射到另一个图像中的最佳方式。
实例2
另一个具体的实例是在医学影像分析中的应用。
假设我们有来自不同医学机构的两组X射线胸片图像,一组用于健康人群,另一组用于患有肺部疾病(如肺炎)的人群。我们的目标是通过最优传输理论来比较这两组图像之间的差异,从而帮助医生更好地理解疾病的特征,提高疾病诊断的准确性。
首先,我们可以将每组图像看作是一个概率分布,其中每个像素的灰度值表示该像素出现在图像中的概率。然后,通过计算两组图像之间的Wasserstein距离,我们可以量化它们之间的差异。这有助于医生们更好地理解健康人群和患有疾病人群之间肺部结构的差异,以及患病区域的特征。
进一步地,通过最优传输理论,我们可以找到将健康人群的肺部结构映射到患病人群的肺部结构的最佳方式。这有助于医生们发现疾病的特征性变化,并且可以用于辅助疾病的早期诊断和预测。
Python代码举例
import numpy as np
from scipy.spatial.distance import cdist
# scipy.spatial.distance 中的 cdist 函数用于计算两组点集之间的距离矩阵。
from ot import emd
# ot 是 OpenOptimalTransport 的缩写,是一个用于最优传输问题的库。
p = np.array([0.2, 0.3, 0.5])
q = np.array([0.1, 0.6, 0.3])C = cdist(np.array([1, 2, 3]).reshape(-1, 1), np.array([1, 2, 3]).reshape(-1, 1))
# cdist 函数计算两组点集之间的距离矩阵。
# 这里计算了一个简单的一维空间中的点集 [1, 2, 3] 与自身的距离矩阵,这个矩阵将被用作最优传输问题中的代价矩阵。
T = emd(p, q, C)
# emd 函数用于计算 Earth Mover's Distance(EMD,也叫 Wasserstein 距离)
# p 和 q 是两个概率分布,C 是代价矩阵。
# T 是最优传输方案,它表示了如何将质量从概率分布 p 转移到概率分布 q 的最佳方式。
print(T)
# T[i, j] 表示将概率分布 p 中第 i 个质量单位转移到概率分布 q 中第 j 个质量单位的量。
相关文章:
最优传输(Optimal Transport)
最优传输(Optimal Transport)是一种数学理论和计算方法,用于描述两个概率分布之间的距离或者对应关系。它的核心概念是如何以最佳方式将一组资源(如质量、能量等)从一个位置传输到另一个位置。 基本概念: …...
MIT-6.824-Lab2,Raft部分笔记|Use Go
文章目录 前记Paper6:RaftLEC5、6:RaftLAB22AtaskHintlockingstructureguide设计与编码 2BtaskHint设计与编码 2CtaskHint question后记 LEC5:GO, Threads, and Raftgo threads技巧raft实验易错点debug技巧 前记 趁着研一考完期末有点点空余…...
使用openeuler 22.03替代CentOS 7.9,建立虚拟机详细步骤
进入浏览器搜索网址下载openeuler 22.03镜像文件 https://mirrors.huaweicloud.com/openeuler/openEuler-22.03-LTS-SP3/ISO/x86_64/openEuler-22.03-LTS-SP3-x86_64-dvd.iso 打开VMware Workstation新建一个虚拟机: 自定义虚拟机位置 加入下载好的openeuler镜像文件…...

代理技术引领出海征程
在数字娱乐的繁荣时代,游戏开发者和发行商们意识到,要在全球市场立足,必须迈向国际化的出海之路。然而,这一旅程面临着跨越网络壁垒、适应多元文化和提升全球连接性的巨大挑战。本文将深入探讨代理技术在游戏行业出海过程中的创新…...
谷粒商城篇章9 ---- P248-P261/P292-P294 ---- 消息队列【分布式高级篇六】
目录 1 消息队列(Message Queue)简介 1.1 概述 1.2 消息服务中两个重要概念 1.3 消息队列主要有两种形式的目的地 1.4 JMS和AMQP对比 1.5 应用场景 1.6 Spring支持 1.7 SpringBoot自动配置 1.7 市面上的MQ产品 2 RabbitMQ 2.1 RabbitMQ简介 2.1.1 RabbitMQ简介 2…...
----生命周期事件)
【Spring连载】使用Spring Data访问 MongoDB(五)----生命周期事件
【Spring连载】使用Spring Data访问 MongoDB(五)----生命周期事件Lifecycle Events 一、实体回调Entity Callbacks1.1 实现实体回调1.2 注册实体回调 二、特定存储的实体回调 一、实体回调Entity Callbacks 1.1 实现实体回调 1.2 注册实体回调 二、特…...

JavaSec 之 SQL 注入简单了解
文章目录 JDBC 注入语句拼接(Statement)修复方案 语句拼接(PrepareStatement)修复方案 预编译 JdbcTemplate修复方案 MyBatisLike 注入Order By 注入In 注入 寒假学了一个月 pwn,真心感觉这玩意太底层学的我生理不适应了,接下来学一段时间 java 安全缓一…...

第十一章——期约与异步函数
ECMAScript 6及之后的几个版本逐步加大了对异步编程机制的支持,提供了令人眼前一亮的新特性。ECMAScript 6新增了正式的Promise(期约)引用类型,支持优雅地定义和组织异步逻辑。接下来几个版本增加了使用async和await关键字定义异步…...

工具方法合集-utils.js
通用 import get from lodash.get import cloneDeep from lodash.clonedeep // 深度clone export function deepClone(obj) {return obj ? cloneDeep(obj) : obj } export function lodashGet(obj, key, defaultValue = ) {//这个 defaultValue 不能给默认 值 会报错;retur…...

安卓11-设置HDMI分辨率流程
安卓11中从设置-显示设置hdmi分辨率流程:framework层通过jni控制底层驱动实现,标准驱动模型 packages\apps\Settings\src\com\android\settings\display\HdmiSettings.javaprivate void updateResolution(final ITEM_CONTROL control, final int index) {showWaitin…...
Vue3+vite搭建基础架构(11)--- 菜单栏功能和Tab页功能实现
Vue3vite搭建基础架构(11)--- 菜单栏功能和Tab页功能实现 说明删除项目中不需要的文件userStore全局属性代码菜单栏代码Tab页代码解决浏览器输入地址时不会打开tab页问题和切换tab页时参数丢失问题 说明 这里记录下自己在Vue3vite的项目实现菜单栏功能和…...

餐饮神秘顾客公司:关于餐饮行业神秘顾客调查注意事项
在餐饮业,顾客体验往往决定品牌的成败。为深入了解顾客需求和感受,许多餐饮企业引入“神秘顾客”调查。然而,此调查并非简单走过场,其中细节和注意事项颇多。餐饮行业神秘顾客调查需注意以下几点: 1. 专业培训&#x…...
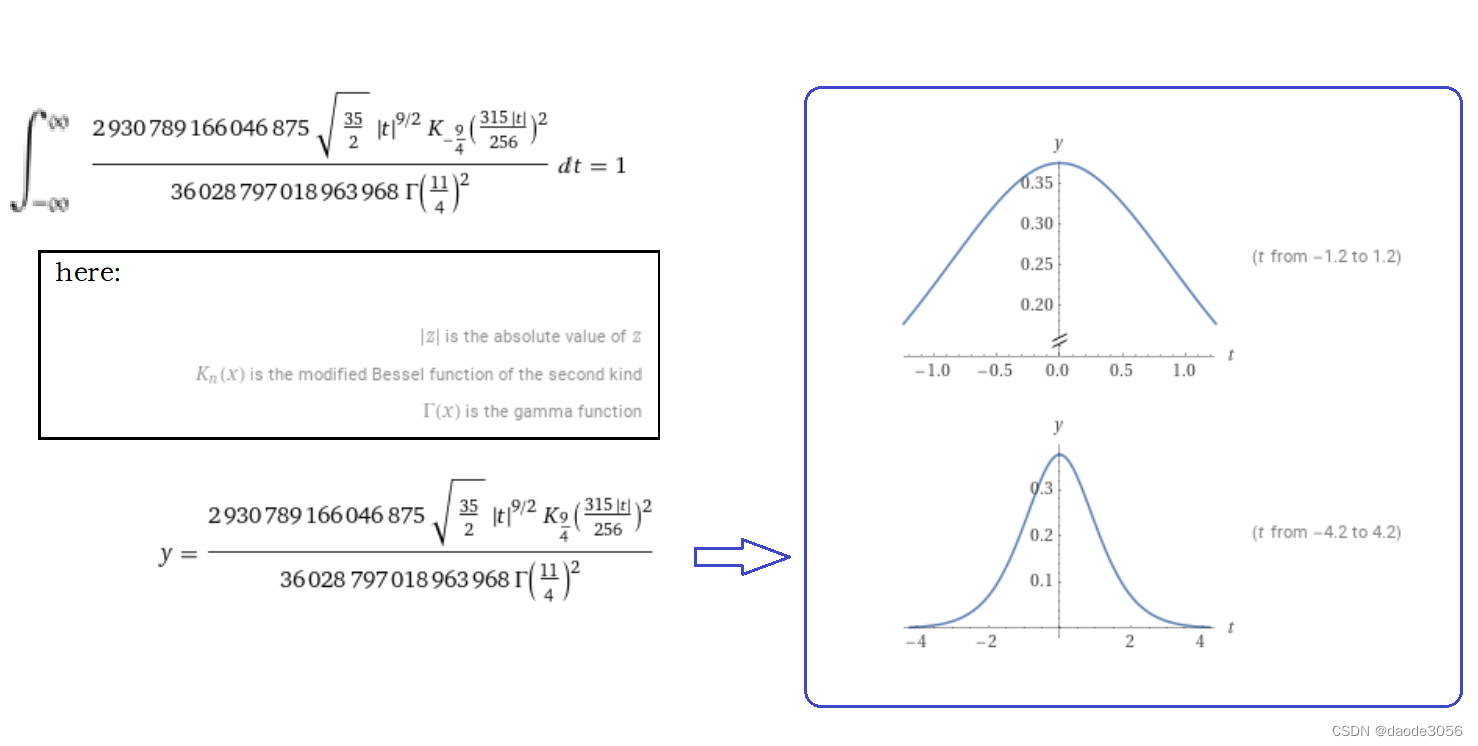
概率密度函数(PDF)与神经网络中的激活函数
原创:项道德(daode3056,daode1212) 在量子力学中,许多现象都是统计的结果,基本上用的是正态分布,然而,从本质上思考,应该还存在低阶的分布,标准的正态分布是它的极限,这样一来,或许在…...
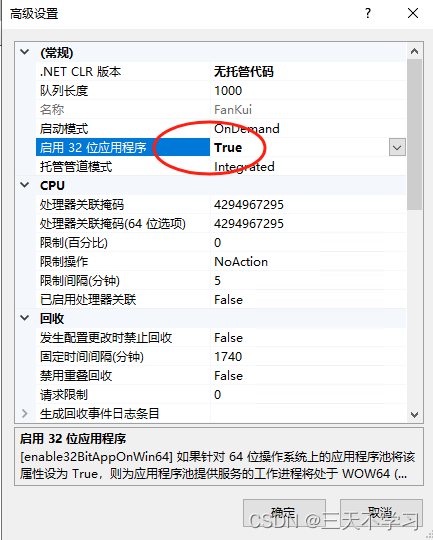
.netcore 6.0/7.0项目迁移至.netcore 8.0 注意事项
1、SqlSugarCore 相关 1.1 主项目添加数据,否则会报数据库连接错误: <InvariantGlobalization>false</InvariantGlobalization> <PropertyGroup><TargetFramework>net8.0</TargetFramework><Nullable>enable</…...
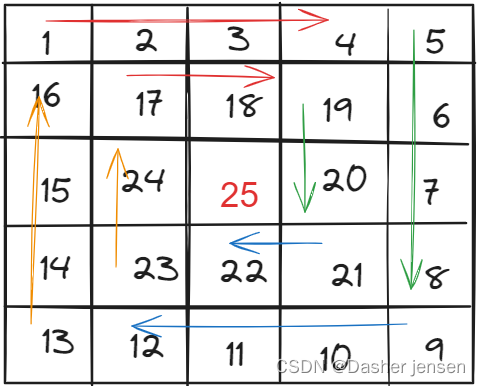
算法打卡day2|数组篇|Leetcode 977.有序数组的平方、 209.长度最小的子数组、59.螺旋矩阵II
算法题 Leetcode 977.有序数组的平方 题目链接: 977.有序数组的平方 大佬视频讲解:977.有序数组的平方 个人思路 第一时间就只想到暴力解法,双重循环一个循环比较一个循环赋值;但这样可能会超时,所以还能用双指针࿰…...

Hive【内部表、外部表、临时表、分区表、分桶表】【总结】
目录 Hive的物种表结构特性 一、内部表 建表 使用场景 二、外部表 建表:关键词【EXTERNAL】 场景: 外部表与内部表可互相转换 三、临时表 建表 临时表横向对比编辑 四、分区表 建表:关键字【PARTITIONED BY】 场景: 五、分桶表 …...

随手写的小程序2 一个nc能控制的程序
小程序源代码 下载: https://download.csdn.net/download/nn_84/88846445?spm1001.2014.3001.5501 请下载 Qt 5.12.12 server.pro : QT gui networkCONFIG c11 console CONFIG - app_bundle# You can make your code fail to compile if it uses deprecated APIs. # In o…...

Android中通过属性动画实现文字轮播效果
前些天发现了一个蛮有意思的人工智能学习网站,8个字形容一下"通俗易懂,风趣幽默",感觉非常有意思,忍不住分享一下给大家。 👉点击跳转到教程 一、创建一个自定义ProvinceView类,具体代码如下 /*** Author: ly* Date: 2024/2/22* D…...

最长的回文串
开始想的简单了,确实没想到奇数字母删去一个后也能用 解法: 桶排序 #include<iostream> #include<vector> #include<algorithm> using namespace std; #define endl \n #define int long long signed main() {int t;cin >> t…...
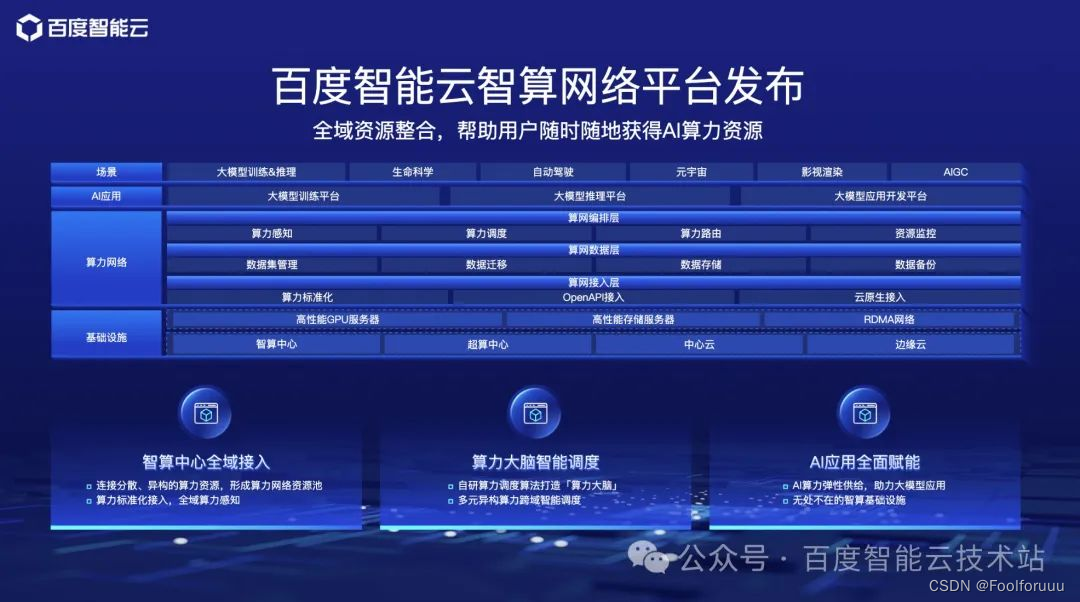
2023 H1 中国边缘公有云服务市场 Top2,百度智能云加速推动分布式云智能化升级
近期,IDC 发布了《中国边缘云市场跟踪研究 2023 H1》。报告显示,2023 上半年,中国边缘公有云服务市场规模 24.3 亿元,同比增速达到 41.8%。 其中,百度智能云以 15.7% 的市场份额位列中国边缘公有云服务市场第二&#…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...
