数据结构与算法-常用排序算法
一、常用排序说明
当涉及排序算法时,理解每个算法的工作原理、时间复杂度和空间复杂度是至关重要的。下面对常用排序算法进行详细说明:
1、冒泡排序(Bubble Sort):
工作原理:比较相邻的元素并交换,每一轮将最大(或最小)的元素移动到数组末尾(或开头)。
时间复杂度:平均情况和最坏情况均为 O(n^2)。
空间复杂度:O(1),原地排序,不需要额外空间。
适用场景:适用于小规模数据集,对稳定性要求高的场景,或者作为教学和理解排序算法的基础。
2、选择排序(Selection Sort):
工作原理:每一轮选择最小(或最大)的元素放在已排序序列的末尾(或开头)。
时间复杂度:平均情况和最坏情况均为 O(n^2)。
空间复杂度:O(1),原地排序,不需要额外空间。
适用场景:适用于小规模数据集,简单易实现,但性能较差。对稳定性要求不高的场景。
3、插入排序(Insertion Sort):
工作原理:将未排序序列中的元素逐个插入到已排序序列中的适当位置。
时间复杂度:平均情况和最坏情况均为 O(n^2)。
空间复杂度:O(1),原地排序,不需要额外空间。
适用场景:适用于小规模或基本有序的数据集,对稳定性要求高的场景,用于改进其他排序算法的一部分。
4、希尔排序(Shell Sort):
工作原理:是插入排序的改进版,通过比较距离较远的元素进行交换,最终使数据基本有序,然后再使用插入排序。
时间复杂度:取决于增量序列的选择,在实践中介于 O(n log^2 n) 和 O(n^2) 之间。
空间复杂度:O(1),原地排序,不需要额外空间。
适用场景:适用于小规模或基本有序的数据集,对稳定性要求高的场景,用于改进其他排序算法的一部分。
5、归并排序(Merge Sort):
工作原理:采用分治法,将数组分成两半,分别排序,然后合并两个有序数组。
时间复杂度:平均情况和最坏情况均为 O(n log n)。
空间复杂度:O(n),需要额外的内存来存储临时数组。
适用场景:适用于小规模或基本有序的数据集,对稳定性要求高的场景,用于改进其他排序算法的一部分。
6、快速排序(Quick Sort):
工作原理:采用分治法,选取一个基准值,将小于基准值的放在左边,大于基准值的放在右边,然后递归地对左右两部分进行排序。
时间复杂度:平均情况为 O(n log n),最坏情况为 O(n^2)。
空间复杂度:取决于实现方式,通常为 O(log n)。
适用场景:适用于大规模数据集,性能优秀且易于实现。常用于实际生产环境中的排序需求。
7、堆排序(Heap Sort):
工作原理:利用堆的性质(最大堆或最小堆),将待排序数组构建成堆,然后每次取出堆顶元素,重新调整堆,直至完成排序。
时间复杂度:平均情况和最坏情况均为 O(n log n)。
空间复杂度:O(1),原地排序,不需要额外空间。
适用场景:适用于大规模数据集,性能稳定且不受输入数据分布情况影响。适合内存受限的情况下进行排序。
8、计数排序(Counting Sort):
工作原理:统计待排序数组中每个元素出现的次数,然后根据元素的值将其放到正确的位置。
时间复杂度:平均情况和最坏情况均为 O(n + k),其中 k 是非负整数的最大值。
空间复杂度:O(n + k),需要额外空间来存储计数数组和输出数组。
适用场景:适用于输入数据的范围相对较小,但数量较大的情况下,可以快速排序。对数字的频率进行统计。
9、桶排序(Bucket Sort):
工作原理:将待排序数据分到有限数量的桶里,每个桶再分别进行排序,最后合并所有桶的结果。
时间复杂度:平均情况为 O(n + k),最坏情况为 O(n^2)。
空间复杂度:O(n + k),需要额外空间来存储计数数组和输出数组。
适用场景:适用于数据均匀分布在一个范围内的情况下,将数据分到多个桶中,然后对每个桶单独进行排序。
10、基数排序(Radix Sort):
工作原理:根据数字位进行排序,先按个位排序,再按十位排序,依次类推,直到最高位排序完成。
时间复杂度:平均情况和最坏情况均为 O(d * (n + k)),其中 d 是数字位数,k 是基数(如 10 进制中的 10)。
空间复杂度:O(n + k),需要额外空间来存储计数数组和输出数组。
适用场景:适用于对数字进行排序的场景通过按位进行排序,每次排序根据数字位数来确定,效率高且稳定。
二、时间复杂度说明
O(1):常数时间复杂度。无论输入规模的大小如何,算法的执行时间都是固定的。例如,访问数组中的一个元素,计算数组的长度等。无论数组中有多少个元素,时间都是恒定的。
O(log n):对数时间复杂度。算法的执行时间与输入规模的对数成正比。典型的例子是二分查找算法。在一个有序数组中查找一个元素时,每次都将搜索空间减半,因此时间复杂度为对数级别。
O(n):线性时间复杂度。算法的执行时间与输入规模成正比,呈线性增长。例如,遍历数组或链表中的所有元素。如果一个数组有 n 个元素,那么对每个元素的访问将花费 O(n) 的时间。
O(n log n):线性对数时间复杂度。典型的例子是快速排序和归并排序等基于比较的排序算法。这些算法的执行时间与输入规模的对数乘以线性成正比。
O(n^2):平方时间复杂度。算法的执行时间与输入规模的平方成正比。例如,嵌套循环的排序算法(如冒泡排序、选择排序),每个元素都需要与其他元素比较。
O(2^n):指数时间复杂度。通常出现在递归算法中,每次递归都会产生指数级别的子问题。例如,求解所有可能的子集或排列问题。
O(n!):阶乘时间复杂度。通常出现在全排列等组合问题中,需要计算所有可能的排列。例如,求解 n 个元素的所有排列可能性的问题。
三、空间复杂度说明
O(1):常数空间复杂度。算法的额外空间使用是一个固定的常数,与输入规模无关。例如,原地排序算法,如冒泡排序、选择排序,不需要额外的空间。
O(log n):对数空间复杂度。算法的额外空间使用与输入规模的对数成正比。例如,递归算法每次调用都会消耗对数级别的栈空间。二分搜索的递归版本就是一个典型的例子。
O(n):线性空间复杂度。算法的额外空间使用与输入规模成正比,呈线性增长。例如,需要一个与输入规模相同大小的数组来存储数据,或者使用一个辅助数组来进行排序。
O(n^2):平方空间复杂度。算法的额外空间使用与输入规模的平方成正比。例如,使用一个二维数组来存储所有可能的组合情况。
O(2^n):指数空间复杂度。算法的额外空间使用与输入规模的指数成正比。通常出现在递归的指数增长情况下,例如,子集生成问题。
O(n!):阶乘空间复杂度。算法的额外空间使用与输入规模的阶乘成正比。通常出现在全排列等组合问题中,需要存储所有可能的排列。
四、代码样例
(一) 冒泡排序(Bubble Sort)
#include <iostream>
using namespace std;void bubbleSort(int arr[], int n) {for (int i = 0; i < n-1; i++) {for (int j = 0; j < n-i-1; j++) {if (arr[j] > arr[j+1]) {swap(arr[j], arr[j+1]);}}}
}int main() {int arr[] = {64, 34, 25, 12, 22, 11, 90};int n = sizeof(arr) / sizeof(arr[0]);bubbleSort(arr, n);cout << "Sorted array: ";for (int i = 0; i < n; i++) {cout << arr[i] << " ";}cout << endl;return 0;
}
(二) 选择排序(Selection Sort)
#include <iostream>
using namespace std;void selectionSort(int arr[], int n) {for (int i = 0; i < n-1; i++) {int min_idx = i;for (int j = i+1; j < n; j++) {if (arr[j] < arr[min_idx]) {min_idx = j;}}swap(arr[i], arr[min_idx]);}
}int main() {int arr[] = {64, 34, 25, 12, 22, 11, 90};int n = sizeof(arr) / sizeof(arr[0]);selectionSort(arr, n);cout << "Sorted array: ";for (int i = 0; i < n; i++) {cout << arr[i] << " ";}cout << endl;return 0;
}
(三) 插入排序(Insertion Sort)
#include <iostream>
using namespace std;void insertionSort(int arr[], int n) {for (int i = 1; i < n; i++) {int key = arr[i];int j = i - 1;while (j >= 0 && arr[j] > key) {arr[j+1] = arr[j];j--;}arr[j+1] = key;}
}int main() {int arr[] = {64, 34, 25, 12, 22, 11, 90};int n = sizeof(arr) / sizeof(arr[0]);insertionSort(arr, n);cout << "Sorted array: ";for (int i = 0; i < n; i++) {cout << arr[i] << " ";}cout << endl;return 0;
}
(四) 希尔排序(Shell Sort)
#include <iostream>
using namespace std;void shellSort(int arr[], int n) {for (int gap = n/2; gap > 0; gap /= 2) {for (int i = gap; i < n; i++) {int temp = arr[i];int j;for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) {arr[j] = arr[j - gap];}arr[j] = temp;}}
}int main() {int arr[] = {64, 34, 25, 12, 22, 11, 90};int n = sizeof(arr) / sizeof(arr[0]);shellSort(arr, n);cout << "Sorted array: ";for (int i = 0; i < n; i++) {cout << arr[i] << " ";}cout << endl;return 0;
}
(五) 归并排序(Merge Sort)
#include <iostream>
#include <vector>
using namespace std;void merge(vector<int>& arr, int l, int m, int r) {int n1 = m - l + 1;int n2 = r - m;vector<int> L(n1), R(n2);for (int i = 0; i < n1; i++)L[i] = arr[l + i];for (int j = 0; j < n2; j++)R[j] = arr[m + 1 + j];int i = 0, j = 0, k = l;while (i < n1 && j < n2) {if (L[i] <= R[j]) {arr[k] = L[i];i++;} else {arr[k] = R[j];j++;}k++;}while (i < n1) {arr[k] = L[i];i++;k++;}while (j < n2) {arr[k] = R[j];j++;k++;}
}void mergeSort(vector<int>& arr, int l, int r) {if (l < r) {int m = l + (r - l) / 2;mergeSort(arr, l, m);mergeSort(arr, m + 1, r);merge(arr, l, m, r);}
}int main() {vector<int> arr = {64, 34, 25, 12, 22, 11, 90};int n = arr.size();mergeSort(arr, 0, n - 1);cout << "Sorted array: ";for (int i = 0; i < n; i++)cout << arr[i] << " ";cout << endl;return 0;
}
(六) 快速排序(Quick Sort)
#include <iostream>
#include <vector>
using namespace std;int partition(vector<int>& arr, int low, int high) {int pivot = arr[high];int i = low - 1;for (int j = low; j < high; j++) {if (arr[j] < pivot) {i++;swap(arr[i], arr[j]);}}swap(arr[i + 1], arr[high]);return i + 1;
}void quickSort(vector<int>& arr, int low, int high) {if (low < high) {int pi = partition(arr, low, high);quickSort(arr, low, pi - 1);quickSort(arr, pi + 1, high);}
}int main() {vector<int> arr = {64, 34, 25, 12, 22, 11, 90};int n = arr.size();quickSort(arr, 0, n - 1);cout << "Sorted array: ";for (int i = 0; i < n; i++)cout << arr[i] << " ";cout << endl;return 0;
}
(七) 堆排序(Heap Sort)
#include <iostream>
#include <vector>
using namespace std;void heapify(vector<int>& arr, int n, int i) {int largest = i;int l = 2 * i + 1;int r = 2 * i + 2;if (l < n && arr[l] > arr[largest])largest = l;if (r < n && arr[r] > arr[largest])largest = r;if (largest != i) {swap(arr[i], arr[largest]);heapify(arr, n, largest);}
}void heapSort(vector<int>& arr) {int n = arr.size();for (int i = n / 2 - 1; i >= 0; i--)heapify(arr, n, i);for (int i = n - 1; i > 0; i--) {swap(arr[0], arr[i]);heapify(arr, i, 0);}
}int main() {vector<int> arr = {64, 34, 25, 12, 22, 11, 90};int n = arr.size();heapSort(arr);cout << "Sorted array: ";for (int i = 0; i < n; i++)cout << arr[i] << " ";cout << endl;return 0;
}
(八) 计数排序(Counting Sort)
#include <iostream>
#include <vector>
using namespace std;void countingSort(vector<int>& arr) {int n = arr.size();int maxVal = *max_element(arr.begin(), arr.end());int minVal = *min_element(arr.begin(), arr.end());int range = maxVal - minVal + 1;vector<int> count(range), output(n);for (int i = 0; i < n; i++)count[arr[i] - minVal]++;for (int i = 1; i < range; i++)count[i] += count[i - 1];for (int i = n - 1; i >= 0; i--) {output[count[arr[i] - minVal] - 1] = arr[i];count[arr[i] - minVal]--;}for (int i = 0; i < n; i++)arr[i] = output[i];
}int main() {vector<int> arr = {64, 34, 25, 12, 22, 11, 90};countingSort(arr);cout << "Sorted array: ";for (int i = 0; i < arr.size(); i++)cout << arr[i] << " ";cout << endl;return 0;
}
(九) 桶排序(Bucket Sort)
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;void bucketSort(vector<float>& arr) {int n = arr.size();vector<vector<float>> buckets(n);for (int i = 0; i < n; i++) {int bucketIndex = n * arr[i];buckets[bucketIndex].push_back(arr[i]);}for (int i = 0; i < n; i++)sort(buckets[i].begin(), buckets[i].end());int index = 0;for (int i = 0; i < n; i++) {for (float num : buckets[i]) {arr[index++] = num;}}
}int main() {vector<float> arr = {0.64, 0.34, 0.25, 0.12, 0.22, 0.11, 0.90};bucketSort(arr);cout << "Sorted array: ";for (int i = 0; i < arr.size(); i++)cout << arr[i] << " ";cout << endl;return 0;
}
(十) 基数排序(Radix Sort)
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;int getMax(vector<int>& arr) {int maxVal = arr[0];for (int i = 1; i < arr.size(); i++) {if (arr[i] > maxVal)maxVal = arr[i];}return maxVal;
}void countingSort(vector<int>& arr, int exp) {int n = arr.size();vector<int> output(n), count(10);for (int i = 0; i < n; i++)count[(arr[i] / exp) % 10]++;for (int i = 1; i < 10; i++)count[i] += count[i - 1];for (int i = n - 1; i >= 0; i--) {output[count[(arr[i] / exp) % 10] - 1] = arr[i];count[(arr[i] / exp) % 10]--;}for (int i = 0; i < n; i++)arr[i] = output[i];
}void radixSort(vector<int>& arr) {int maxVal = getMax(arr);for (int exp = 1; maxVal / exp > 0; exp *= 10)countingSort(arr, exp);
}int main() {vector<int> arr = {64, 34, 25, 12, 22, 11, 90};radixSort(arr);cout << "Sorted array: ";for (int i = 0; i < arr.size(); i++)cout << arr[i] << " ";cout << endl;return 0;
}
相关文章:

数据结构与算法-常用排序算法
一、常用排序说明 当涉及排序算法时,理解每个算法的工作原理、时间复杂度和空间复杂度是至关重要的。下面对常用排序算法进行详细说明: 1、冒泡排序(Bubble Sort): 工作原理:比较相邻的元素并交换&am…...

链表之“无头单向非循环链表”
目录 编辑 1.顺序表的问题及思考 2.链表 2.1链表的概念及结构 2.2无头单向非循环链表的实现 1.创建结构体 2.单链表打印 3.动态申请一个节点 3.单链表尾插 4.单链表头插 5.单链表尾删 6.单链表头删 7.单链表查找 8.单链表在pos位置之前插入x 9.单链表删除pos位…...
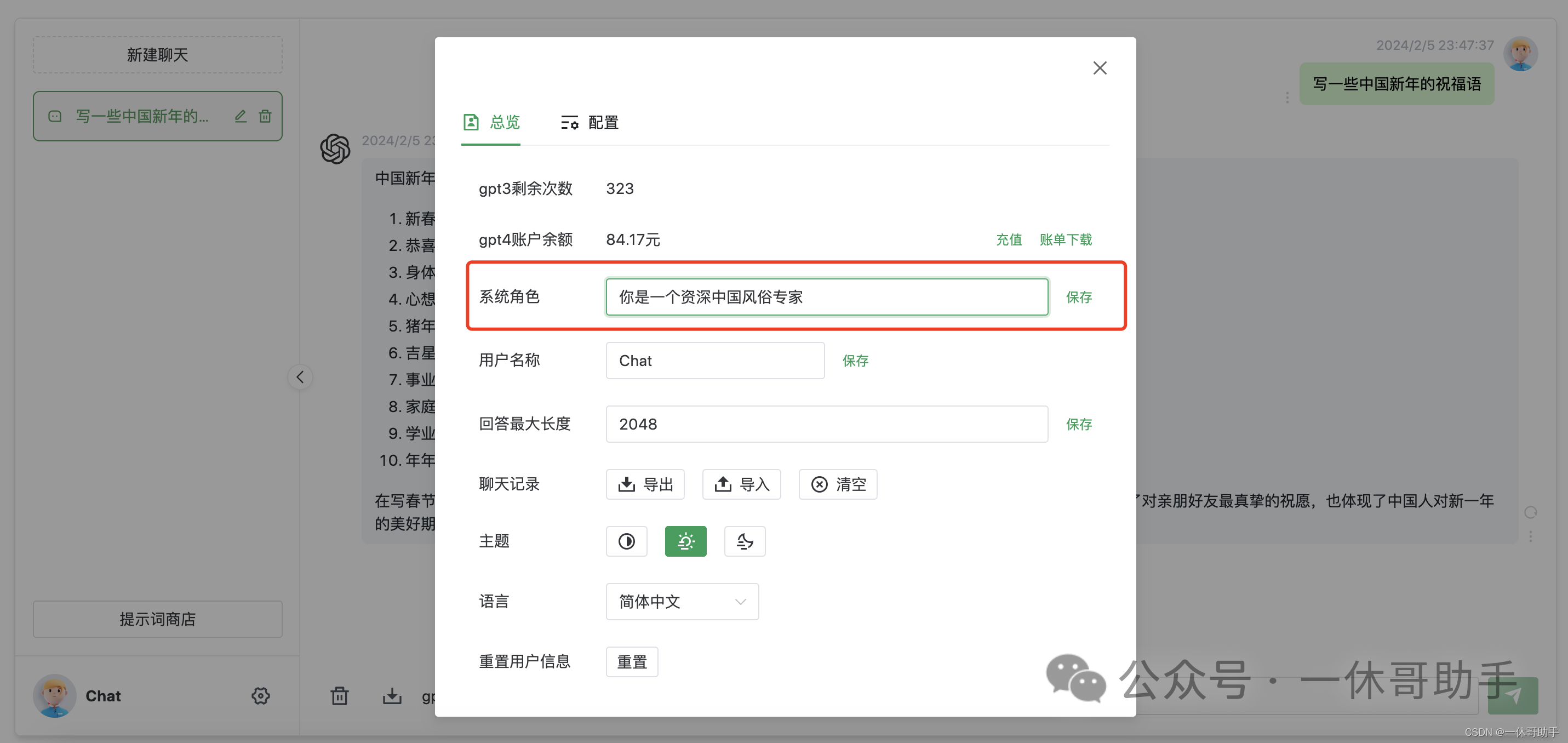
一休哥助手网页版如何使用
一休哥助手网页版可以使用GPT4提问了,具体操作流程如下: 1.登录网页版一休哥助手(首次打开页面时,初始化久一点,请耐心等一下) https://www.fudai.fun 2.登录后就可以使用GPT4了 3.你还可以自定义系统角色…...

个人博客系统测试
文章目录 一、项目介绍二、测试1. 功能测试2. 自动化测试(1)添加相关依赖(2)新建包并在报下创建测试类(3)亮点及难点 一、项目介绍 个人博客系统采用前后端分离的方法来实现,同时使用了数据库来…...

智慧应急的未来:物联网技术引领智慧应急发展新趋势
一、引言 随着社会的快速发展,各类突发事件频繁发生,对社会的安全稳定构成了严重威胁。传统的应急管理模式已难以满足现代社会对安全保障的需求,急需探索新型的应急管理手段。在这个背景下,智慧应急应运而生,以其高效…...
)
字符串摘要(C语言)
题目描述 给定一个字符串的摘要算法,请输出给定字符串的摘要值。 去除字符串中非字母的符号。如果出现连续字符(不区分大小写),则输出:该字符(小写) 连续出现的次数。如果是非连续的字符&…...
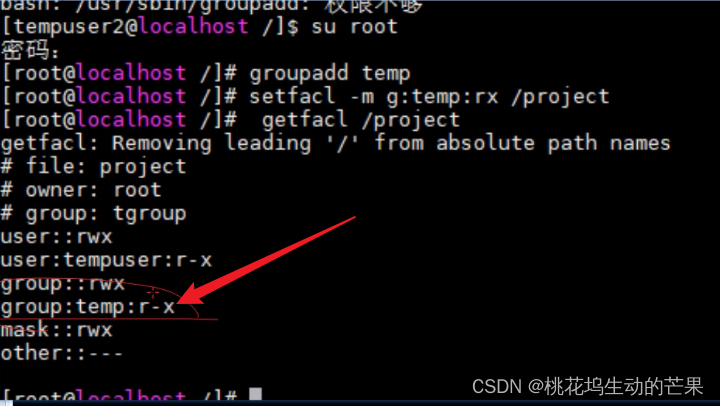
Linux进一步研究权限-----------ACL使用
一、使用情况 1.1、场景: 某个大公司,在一个部门,有一个经理和手下有两个员工,在操控一个Linux项目,项目又分为三期做,然而一期比较重要,经理带着员工做完了,公司就觉得技术难点已经做完攻克了࿰…...

剪辑视频调色软件有哪些 剪辑视频软件哪个最好 剪辑视频怎么学 剪辑视频的方法和步骤 会声会影2024 会声会影视频制作教程
看了很多调色教程,背了一堆调色参数,可最终还是调不出理想的效果。别再怀疑自己了,不是你的剪辑技术不行,而是剪辑软件没选对。只要掌握了最基本的调色原理,一款适合自己的视频剪辑软件是很容易出片的。 有关剪辑视频…...
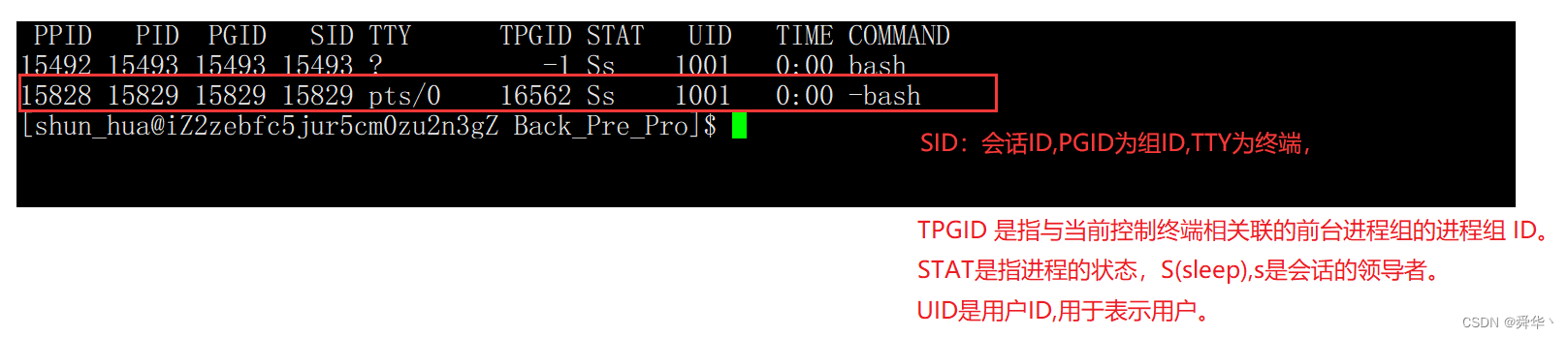
【Linux进阶之路】Socket —— “UDP“ “TCP“
文章目录 一、再识网络1. 端口号2. 网络字节序列3.TCP 与 UDP 二、套接字1.sockaddr结构2.UDP1.server端1.1 构造函数1.2 Init1.3 Run 2.客户端1.Linux2.Windows 3.TCP1. 基本接口2. 客户端3. 服务端1.版本12.版本23.版本34.版本4 三、守护进程尾序 一、再识网络 1. 端口号 在…...

一些用 GPT 翻译的计算机科学/人工智能 PDF 讲义
3D成像.pdf3D成像技术.pdf3D点云分析.pdfAAAI 2019 笔记.pdfCMU 10.708 概率图模型讲义.pdfCMU 15-312 编程语言基础讲义.pdfCMU 15-411 编译器设计讲义.pdfCMU 15-819 同伦类型论讲义.pdfCMU 15-819O 程序分析讲义.pdfCUNY CSci335 软件设计与分析 3 讲义.pdfDixie IT4500 信息…...
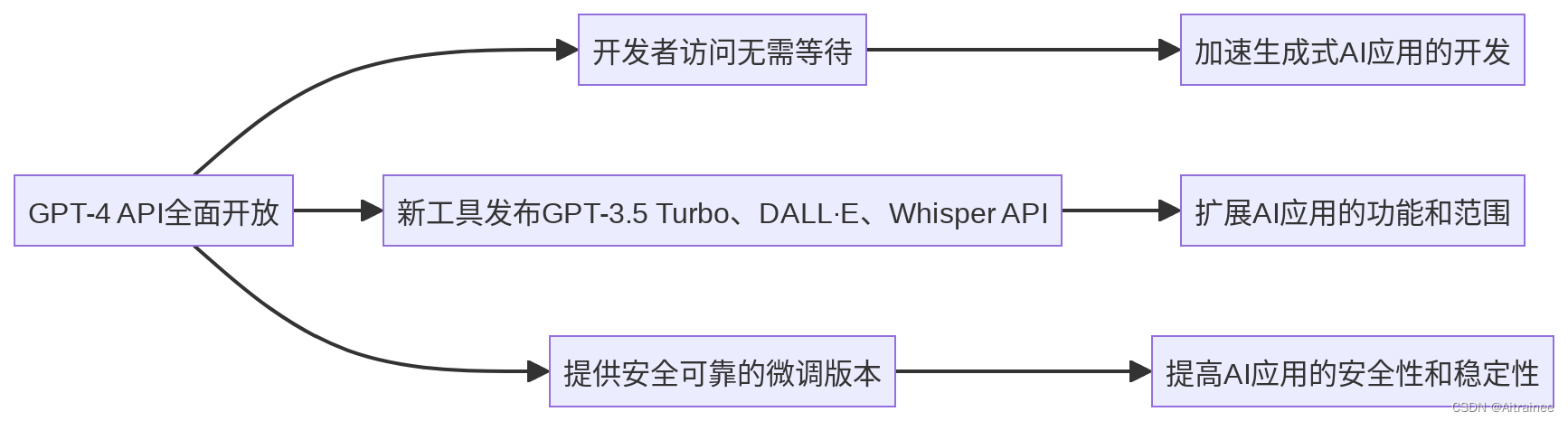
重大更新:GPT-4 API 现全面向公众开放!
重大更新:GPT-4 API 现全面向公众开放! 在 AIGC(人工智能生成内容)领域内,我们一直致力于跟踪和分析如 OpenAI、百度文心一言等大型语言模型(LLM)的进展及其在实际应用中的落地情况。我们还专注…...
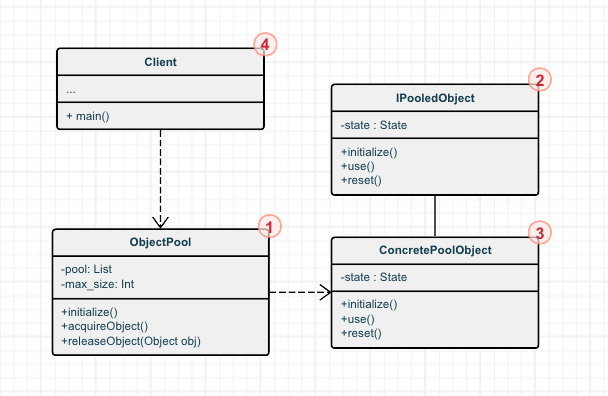
【Python笔记-设计模式】对象池模式
一、说明 用于管理对象的生命周期,重用已经创建的对象,从而减少资源消耗和创建对象的开销 (一) 解决问题 主要解决频繁创建和销毁对象所带来的性能开销问题。如数据库连接、线程管理、网络连接等,对象的创建和销毁成本相对较高,…...

反序列化 [NPUCTF2020]ReadlezPHP1
打开题目 直接查看源代码 打开源代码发现了个./time.php?source 访问一下 审计代码: 现存在反序列化语句:$ppp unserialize($_GET["data"]);和执行漏洞:echo $b($a); 发现在__destruct()方法里面有 echo $b($a); 这个是php的…...

AI技术那些事儿:揭开潜伏在你生活中的高科技小能手
你有没有发现,现在的生活里有些“看不见”的聪明家伙,它们时时刻刻在帮咱们忙活呢?从早上用语音命令打开窗帘、播报新闻,到晚上喊一声关灯睡觉,这些都离不开人工智能(简称AI)的助攻。今天咱就掰…...
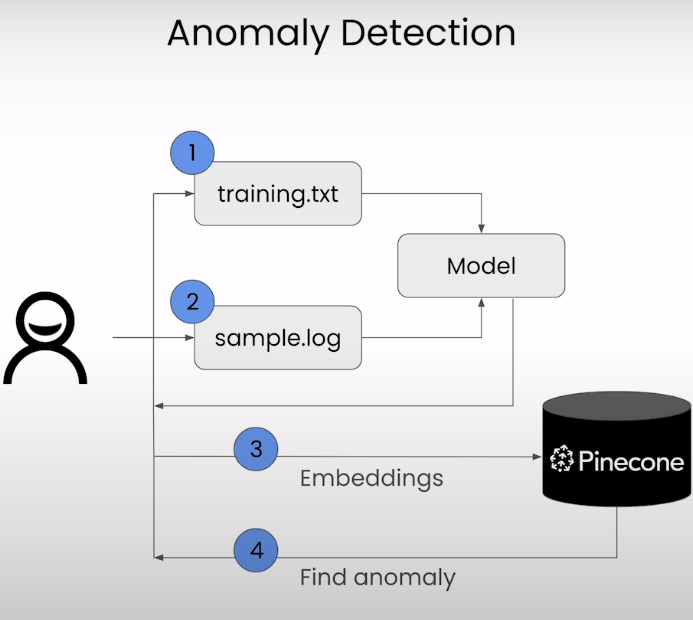
使用向量数据库pinecone构建应用06:日志系统异常检测 Anomaly Detection
Building Applications with Vector Databases 下面是这门课的学习笔记:https://www.deeplearning.ai/short-courses/building-applications-vector-databases/ Learn to create six exciting applications of vector databases and implement them using Pinecon…...

抽象工厂模式 Abstract Factory
1.模式定义: 提供一个创建一系列相关或互相依赖对象的接口,而无需指定它们具体的类 2. 应用场景: 程序需要处理不同系列的相关产品,但是您不希望它依赖于这些产品的 具体类时, 可以使用抽象工厂 3.优点: 1.可以确信你从工厂得到的产品彼…...

掌握 Android 中的 RecyclerView 优化
掌握 Android 中的 RecyclerView 优化 一、RecyclerView Pool以及何时使用它二、onCreateViewHolder 和 onBindViewHolder三、优化 RecyclerView 的不同方法四、视图无效与请求布局五、ViewHolder模式六、默认的废料和脏视图类型七、结论 RecyclerView 是 Android 中一个功能强…...
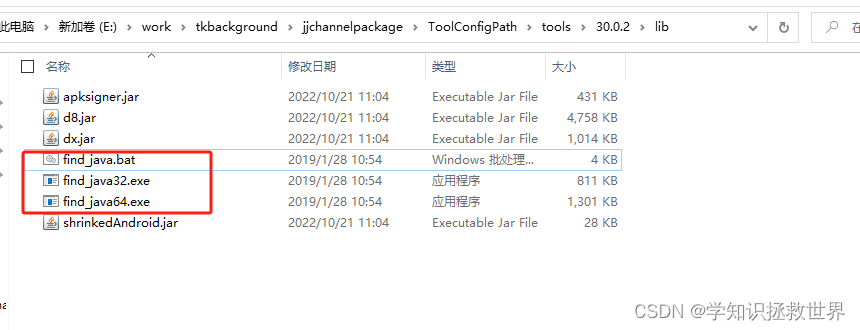
Android platform tool中d8.bat不生效
d8.bat因找不到java_exe文件,触发EOF d8.bat中之前代码为: set java_exe if exist "%~dp0..\tools\lib\find_java.bat" call "%~dp0..\tools\lib\find_java.bat" if exist "%~dp0..\..\tools\lib\find_java.bat" …...
WSL安装Ubuntu22.04,以及深度学习环境的搭建
安装WSL 安装 WSL 2 之前,必须启用“虚拟机平台”可选功能。 计算机需要虚拟化功能才能使用此功能。 以管理员身份打开 PowerShell 并运行: dism.exe /online /enable-feature /featurename:VirtualMachinePlatform /all /norestart下载 Linux 内核更…...

【PTA|选择题|期末复习】结构体
2-1 For the following declarations,assignment expression_is not correct. struct Student {long num;char name[28];}st1,st2{101,"Tom"},*p&st1; 〇 A.st1 st2 ◎ B.p->name st2.name O C p->num st2.num 〇 D,*pst2 2-2 下面定义结构变量的语…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...
