【算法与数据结构】链表、哈希表、栈和队列、二叉树(笔记二)
文章目录
- 四、链表理论
- 五、哈希表理论
- 五、栈和队列理论
- 5.1 单调栈
- 六、二叉树理论
- 6.1 树的定义
- 6.2 二叉树的存储方式
- 6.3 二叉树的遍历方式
- 6.4 高度和深度
最近博主学习了算法与数据结构的一些视频,在这个文章做一些笔记和心得,本篇文章就写了一些基础算法和数据结构的知识点,具体题目解析会放在另外一篇文章。在学习时已经有C, C++的基础。文章附上了学习的代码,仅供大家参考。如果有问题,有错误欢迎大家留言。算法与数据结构一共有三篇文章,剩余文章可以在 【CSDN文章】晚安66博客文章索引找到。
四、链表理论
单链表:由一个个节点组成,每个节点由一个数据域和一个指针域组成,数据域放数据,指针域指向下一个节点,链表入口节点叫做head,最后一个节点的next指针指向NULL(空指针)。
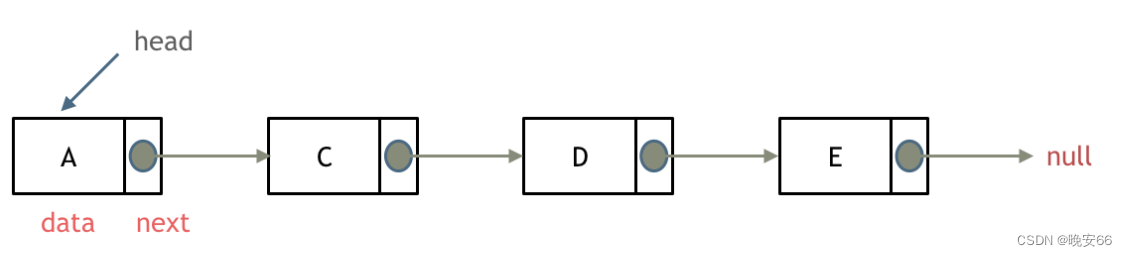
双链表:在单链表的基础上增加了一个指针域,这个指针域指向前一个节点,head的prev指针指向NULL。双链表既可以向前查,也可以向后查。

循环链表:链表的首尾相连。循环链表可以解决约瑟夫环问题。
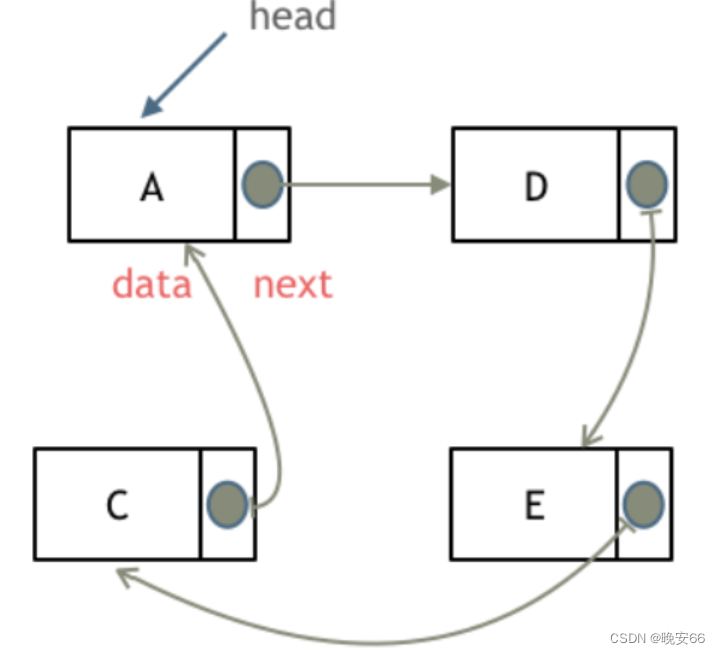
数组在内存中是连续分布的,但是链表不是连续分布的,它通过指针域的指针链接在内存中的各个节点。
链表定义方式:
// 单链表
struct ListNode {int val; // 节点上存储的元素ListNode *next; // 指向下一个节点的指针ListNode(int x) : val(x), next(NULL) {} // 节点的构造函数
};
初始化链表:
// 法一
ListNode* head = new ListNode(5);
// 法二
ListNode* head = new ListNode();
head->val = 5;
删除和添加节点:
假如想删除图中D节点,那么我们将C节点指针指向E节点,然后释放D的内存(C++需要手动释放,Java,Python有内存回收机制,不需要手动释放)。
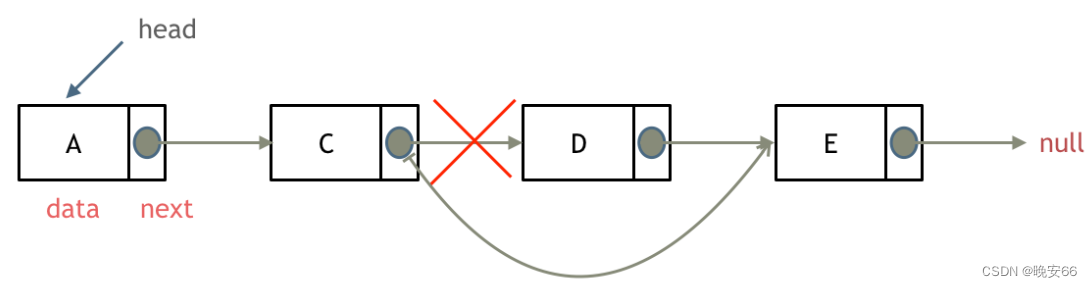
假如要添加F节点,将C节点的指针指向F,F指针指向D即可。
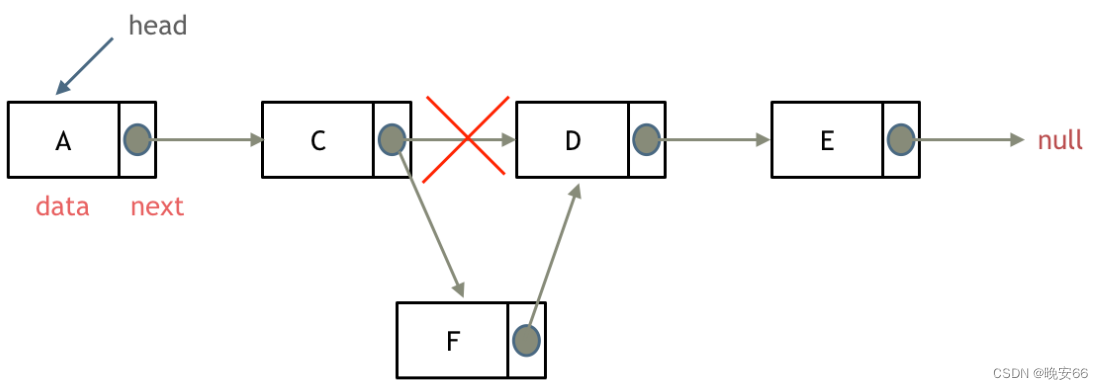
查询:
链表查询是比较费劲的,例如想找第10个节点,那么得从第一个节点开始,按指针域一个一个找,找到第九个节点才能找到第十个节点。因此,链表查询时间复杂度为 O ( n ) O(n) O(n)
| 项目 | 插入/删除 | 查询 | 使用场景 |
|---|---|---|---|
| 数组 | O ( n ) O(n) O(n) | O ( 1 ) O(1) O(1) | 数据量固定,频繁查询,较少增删 |
| 链表 | O ( 1 ) O(1) O(1) | O ( n ) O(n) O(n) | 数据量不固定,频繁增删, 较少查询 |
五、哈希表理论
哈希表可以通过索引直接访问表中的元素。哈希表一般用来快速判断一个元素是否出现在集合里,但哈希法是牺牲空间换取时间,因为要使用额外的数组set或map才能实现快速查找。举个例子,班级里是否有小明这个同学,如果要用枚举时间复杂度为 O ( n ) O(n) O(n),但如果哈希表只需要 O ( 1 ) O(1) O(1)就可以做到。
在初始化时,只需要把全班的名字存在哈希表里,查询的时候通过姓名直接可以知道是否有这位同学。哈希表通过哈希函数(hash funciton)将学生姓名映射到哈希表上。
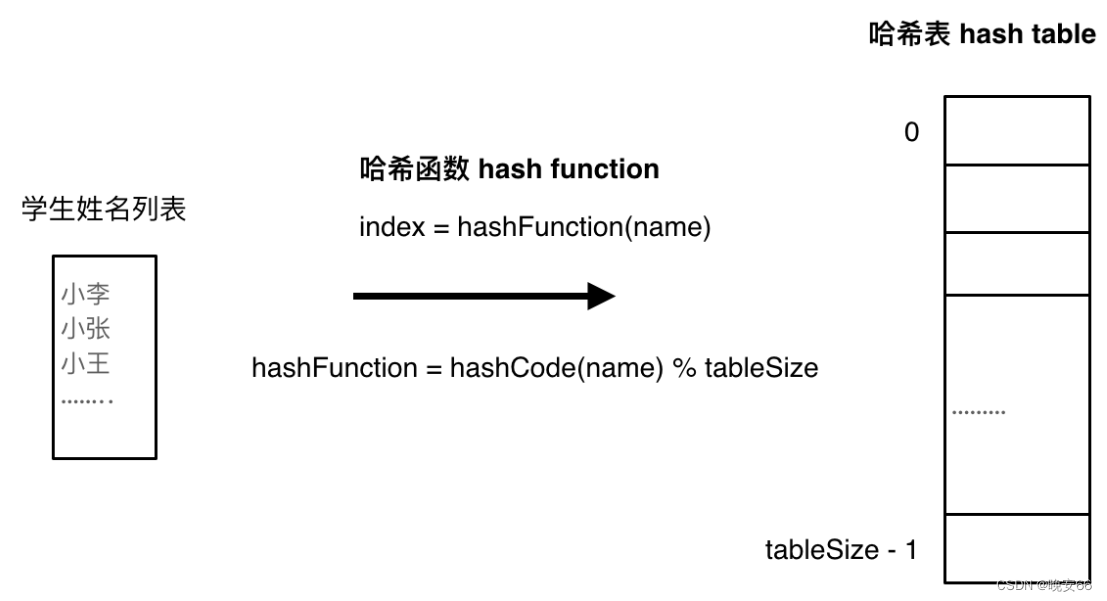
工作原理:如上图所示,哈希函数将姓名转换成数值索引(一般通过特定编码方式),然后按索引在哈希表上得到目标数据。同时为了保证哈希函数计算的索引一定落在哈希表中,还做了取模操作。有时候,学生数量会大于哈希表长度,不同学生会得到同一个索引,也就是映射到哈希表上同一个位置,也就出现所谓的哈希碰撞问题。
哈希碰撞解决办法:
- 1、拉链法:在碰撞位置引入链表,链表指向依次指向不同的学生。拉链法要注意适当选择哈希表大小,充分利用哈希表内存,同时不要生成太长的链表。
- 2、线性探测法:当发生碰撞时,就找表的下一个空位方置。因此,一定要保证哈希表大小大于数据大小。
常用的哈希表有:
- 数组
- 集合(set)
- 映射(map)
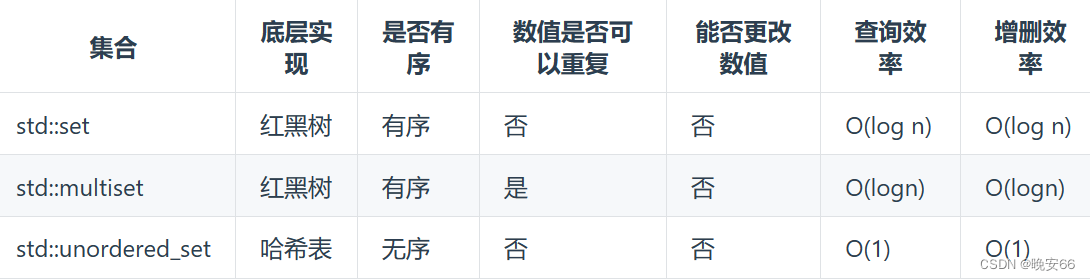
在C++中,set和map提供了下面几种形式,使用集合来解决问题时,优先使用unordered_set,它底层用哈希表实现,查询效率和增删效率最高。只有处理有序数据时用set或者multiset(二者区别在于值能否重复)。
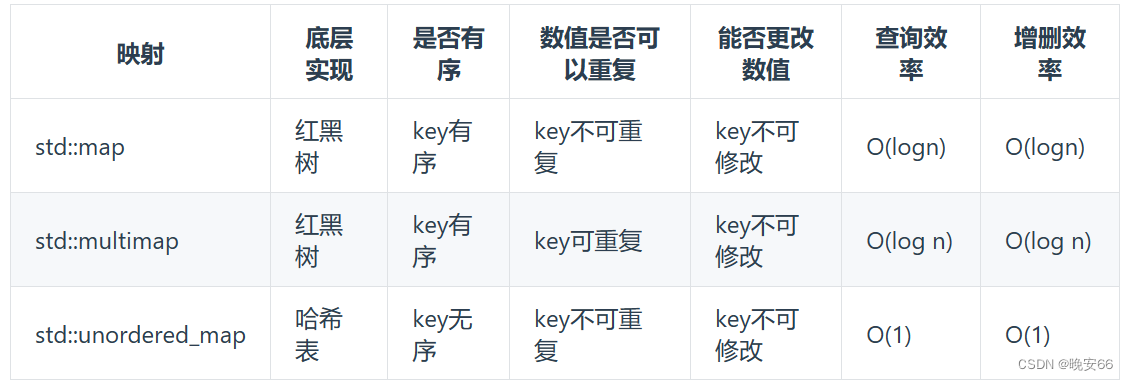
虽然set、multiset、 map和multimap底层使用红黑树实现的,但是使用方式还是哈希表的key和value方式,同属于映射方法,同样可以归类到哈希法中。此外,红黑树是一种平衡二叉搜索树,key值是有序的,但key值不能修改,改动key值会导致整颗树错乱,所以智能删除和增加。map当中对key有限制,不可修改,value没有限制。
五、栈和队列理论
首先是关于栈和队列的元素进出关系:栈是先进后出,队列是先进先出。栈提供push 和 pop 等等接口,所有元素必须符合先进后出规则,所以栈不提供走访功能,也不提供迭代器(iterator)。 不像是set 或者map 提供迭代器iterator来遍历所有元素。

栈是以底层容器完成其所有的工作,对外提供统一的接口,我们可以控制使用哪种容器来实现栈的功能(栈是可插拔),例如vector,list,deque等等。所以STL中栈往往不被归类为容器,而被归类为container adapter(容器适配器)。目前最常见的SGI STL(STL库的其中一个版本),如果没有指定底层实现,默认以deque(双向队列)缺省为底层容器,只要封住一端,开通另一端就可以实现栈的逻辑。
也可以指定vector为底层实现:
std::stack<int, std::vector<int> > third; // 使用vector为底层容器的栈
队列的情况是一样的,队列中先进先出的数据结构,同样不允许有遍历行为,不提供迭代器, SGI STL中队列一样是以deque为缺省情况下的底部结构。队列也不归为容器,也是容器适配器。
std::queue<int, std::list<int>> third; // 定义以list为底层容器的队列
5.1 单调栈
单调栈问题长是针对一个一维数组,要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置。单调栈可以在 O ( n ) O(n) O(n)的时间复杂度内找到每一个元素的右边第一个比它大的元素位置。单调栈的本质是空间换时间,优点是整个数组只需遍历一次。我们使用一个栈来保存遍历过程中的元素。因为我们遍历数组的时候,我们不知道之前都遍历了哪些元素,以至于遍历一个元素找不到是不是之前遍历过一个更小的,所以我们需要用一个容器(这里用单调栈)来记录我们遍历过的元素。
单调栈问题需要考虑以下几点:
-
- 单调栈里面存放的元素是什么?
-
- 单调栈是递增还是递减的?
这里的递增或者递减的顺序指的是从栈底到栈顶(栈头)的顺序,C++中使用STL库可以用st.top()来访问栈顶。
- 单调栈是递增还是递减的?
六、二叉树理论
6.1 树的定义
首先引入树的度的概念:结点拥有的子树个数称为结点的度,比如下图中结点3和结点4的度分别为3和2。对于树而言,树的度是结点最大的度,下面这棵树的度为4(结点1的度)。

二叉树是指树的度最大为2的树。满二叉树:如果一棵树只有度为0和度为2的节点,并且度为0的节点在同一层上,则这棵二叉树为满二叉树。如下图所示,这是一棵满二叉树。这棵二叉树为满二叉树,也可以说深度为k,有2^k-1个节点的二叉树。

完全二叉树:在完全二叉树中,除了最底层节点可能没有填满以外,其余每层节点数量都达到最大值,并且最下面一层节点都集中在该层的最左边若干位置。若底层为第k层,则该层包含 [ 1 , 2 k − 1 ] [1, 2^{k-1}] [1,2k−1]个节点。
在【算法和数据结构】347、LeetCode前 K 个高频元素中提到的优先级队列。实际上,优先级队列其实是一个堆,堆就是一棵完全二叉树,同时保证父子节点的顺序关系。下图当中第三棵树就不是一棵完全二叉树。

二叉搜索树:又叫二叉排序树。它具有下面三个特点:
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树

平衡二叉排序树:又被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。下图当中第三棵树就不是一棵平衡二叉树,左右两个子树的高度差绝对值超过了1。

C++中map、set、multimap,multiset的底层实现都是平衡二叉搜索树,所以map、set的增删操作的时间复杂度是 l o g ( n ) log(n) log(n)。unordered_map、unordered_set底层实现是哈希表, 增删操作的时间复杂度为 O ( 1 ) O(1) O(1)。详细内容可以看本文第五节。
6.2 二叉树的存储方式
二叉树可以用链式存储,也可以顺序存储。那么链式存储方式就用指针, 顺序存储的方式就是用数组。链式存储如下图所示:

顺序存储如下图所示,在遍历时,假设父节点为i那么它的左孩子就是 i ∗ 2 + 1 i*2+1 i∗2+1,右孩子就是 i ∗ 2 + 2 i*2+2 i∗2+2。相较于链式存储,顺序存储方式比较不容易理解,也不直观,所以一般我们用链式存储二叉树。

6.3 二叉树的遍历方式
二叉树主要有两种遍历方式,这两种也是图论当中最基本的两种遍历方式。
- 深度优先遍历:先往深处走,遇到叶子节点再往回走。
- 广度优先遍历:一层一层的去遍历。
在上面两种方式的基础之上进一步拓展,有如下的分类:
-
深度优先遍历
- 前序遍历(递归法、迭代法)
- 中序遍历(递归法、迭代法)
- 后序遍历(递归法、迭代法)
-
广度优先遍历
- 层次遍历(迭代法)
前中后是指中间节点的遍历顺序,是在前、中或者是后。例如,前序遍历:中左右;中序遍历:左中右;后序遍历:左右后。

递归法和迭代法是这两种遍历的实现方法。深度优先遍历一般是用递归的方式实现,也就是说,用递归来实现前中后遍历比较方便。栈其实就是递归的一种实现结构,前中后遍历的逻辑也可以用栈使用非递归的方式来实现。广度优先遍历的实现一般使用队列来实现,队列是先进先出的结构,这样才能一层层的遍历二叉树。
链式存储二叉树节点的定义方式如下,相较于链表节点,二叉树节点与其定义差不多,二叉树节点有两个指针分别指向了其左右孩子。
树节点定义:
// 树节点定义
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
迭代法实现前中后遍历:
class Solution {
public:// 前序遍历void traversal_preOrder(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;vec.push_back(cur->val); // 中traversal_preOrder(cur->left, vec); // 左traversal_preOrder(cur->right, vec); // 右}// 中序遍历void traversal_midOrder(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return; traversal_midOrder(cur->left, vec); // 左vec.push_back(cur->val); // 中traversal_midOrder(cur->right, vec); // 右}// 后序遍历void traversal_postOrder(TreeNode* cur, vector<int>& vec) {if (cur == NULL) return;traversal_postOrder(cur->left, vec); // 左traversal_postOrder(cur->right, vec); // 右vec.push_back(cur->val); // 中}vector<int> preorderTraversal(TreeNode* root) {vector<int> result;traversal_preOrder(root, result);return result;}
};
6.4 高度和深度
高度和深度是相反的表示,深度是从上到下数,而高度是从下往上数。深度指从根节点到该节点最长简单路径边数,而高度指从该节点到叶子节点的最长简单路径边数。叶子节点是指没有子节点的节点。假设根节点的深度和叶子节点的高度为1,那么树的深度和高度是相等的,而对其他节点来说高度和深度不一定相等。例如下图当中,8这个节点的深度为2,高度为4。

end
相关文章:

【算法与数据结构】链表、哈希表、栈和队列、二叉树(笔记二)
文章目录 四、链表理论五、哈希表理论五、栈和队列理论5.1 单调栈 六、二叉树理论6.1 树的定义6.2 二叉树的存储方式6.3 二叉树的遍历方式6.4 高度和深度 最近博主学习了算法与数据结构的一些视频,在这个文章做一些笔记和心得,本篇文章就写了一些基础算法…...

bugku3
前女友 md5 进去又是讴歌乱进的东西 源代码 看到code.txt,访问一下 <?php if(isset($_GET[v1]) && isset($_GET[v2]) && isset($_GET[v3])){$v1 $_GET[v1];$v2 $_GET[v2];$v3 $_GET[v3];if($v1 ! $v2 && md5($v1) md5($v2)){if(!strcmp($v3,…...

相机的白平衡
相机的白平衡是指相机根据拍摄环境的光源色温,调整图像中白色看起来应该是白色的功能。白平衡的设置对于确保图像中的颜色准确性非常重要,因为不同光源的色温会使白色看起来有不同的色调。 通常,相机提供了一些预设的白平衡模式,…...
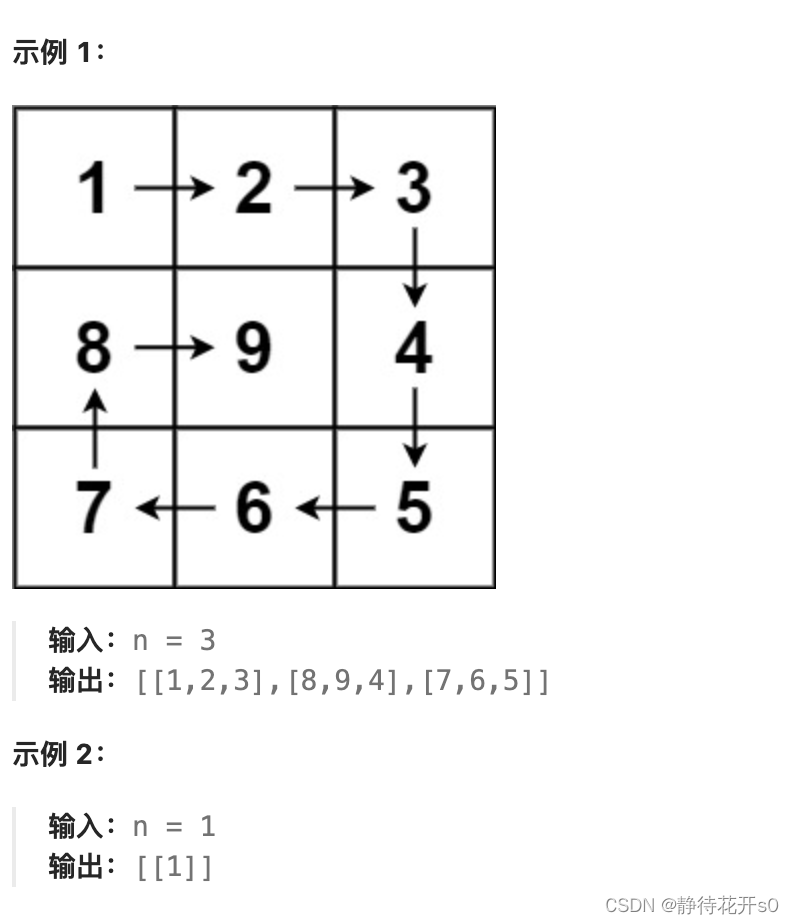
刷题日记-Day2- Leedcode-977. 有序数组的平方,209. 长度最小的子数组,59. 螺旋矩阵 II-Python实现
刷题日记Day2 977 有序数组的平方209. 长度最小的子数组59. 螺旋矩阵 II 977 有序数组的平方 链接:https://leetcode.cn/problems/squares-of-a-sorted-array/description/ 给你一个按 非递减顺序 排序的整数数组 nums,返回 每个数字的平方 组成的新数组…...
的安全上下文))
Linux命令-chcon命令(修改对象(文件)的安全上下文)
说明 chcon命令 是修改对象(文件)的安全上下文,比如:用户、角色、类型、安全级别。也就是将每个文件的安全环境变更至指定环境。使用 --reference 选项时,把指定文件的安全环境设置为与参考文件相同。chcon命令位于 /…...
【漏洞复现】大华DSS视频管理系统信息泄露漏洞
Nx01 产品简介 大华DSS数字监控系统是一个在通用安防视频监控系统基础上设计开发的系统,除了具有普通安防视频监控系统的实时监视、云台操作、录像回放、报警处理、设备治理等功能外,更注重用户使用的便利性。 Nx02 漏洞描述 大华DSS视频管理系统存在信…...
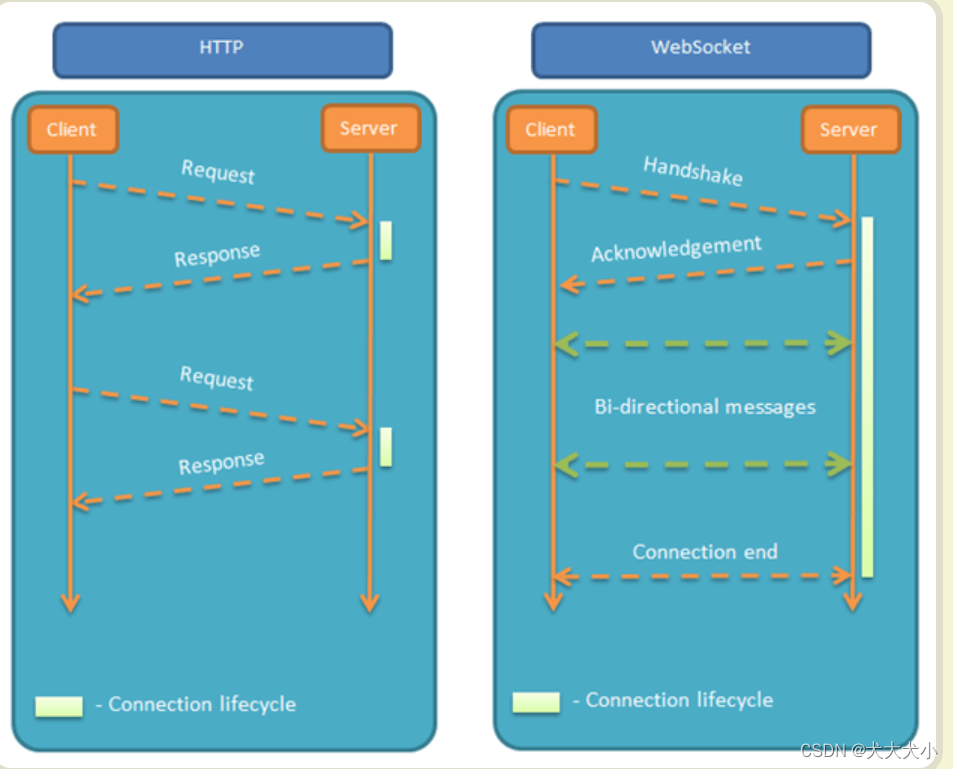
websocket了解下
websocket请求长啥样 GET /chat HTTP/1.1 Host: example.com Upgrade: websocket Connection: Upgrade Sec-WebSocket-Key: dGhlIHNhbXBsZSBub25jZQ Sec-WebSocket-Version: 13 啥是websocket websocket是http的一种,服务器可以主动向客户端推送信息,…...

docker install private registry 【docker 安装 registry 仅证书认证】
预备条件: 安装docker 我们设定镜像仓库域名为registry01.dev.com 配置/etc/hosts 192.168.23.51 registry01.dev.com安装 registry #!/bin/bashreg_ip$1 reg_n$2 reg_port$3if [ $# -eq 0 ]; thenecho "Usage: $0 [reg_ip] [registry_name]"echo &q…...
JavaWeb——004Maven SpringBootWeb入门
一、Maven 1、什么是maven? 2、Maven的作用是什么?(3种) 1.1、方便的依赖管理 依赖管理:有了Maven,我们就不用再手动导入Jar包了,我们只需要在配置文件当中,简单描述一下项目所需要…...

数据结构与算法-常用排序算法
一、常用排序说明 当涉及排序算法时,理解每个算法的工作原理、时间复杂度和空间复杂度是至关重要的。下面对常用排序算法进行详细说明: 1、冒泡排序(Bubble Sort): 工作原理:比较相邻的元素并交换&am…...

链表之“无头单向非循环链表”
目录 编辑 1.顺序表的问题及思考 2.链表 2.1链表的概念及结构 2.2无头单向非循环链表的实现 1.创建结构体 2.单链表打印 3.动态申请一个节点 3.单链表尾插 4.单链表头插 5.单链表尾删 6.单链表头删 7.单链表查找 8.单链表在pos位置之前插入x 9.单链表删除pos位…...
一休哥助手网页版如何使用
一休哥助手网页版可以使用GPT4提问了,具体操作流程如下: 1.登录网页版一休哥助手(首次打开页面时,初始化久一点,请耐心等一下) https://www.fudai.fun 2.登录后就可以使用GPT4了 3.你还可以自定义系统角色…...

个人博客系统测试
文章目录 一、项目介绍二、测试1. 功能测试2. 自动化测试(1)添加相关依赖(2)新建包并在报下创建测试类(3)亮点及难点 一、项目介绍 个人博客系统采用前后端分离的方法来实现,同时使用了数据库来…...

智慧应急的未来:物联网技术引领智慧应急发展新趋势
一、引言 随着社会的快速发展,各类突发事件频繁发生,对社会的安全稳定构成了严重威胁。传统的应急管理模式已难以满足现代社会对安全保障的需求,急需探索新型的应急管理手段。在这个背景下,智慧应急应运而生,以其高效…...
)
字符串摘要(C语言)
题目描述 给定一个字符串的摘要算法,请输出给定字符串的摘要值。 去除字符串中非字母的符号。如果出现连续字符(不区分大小写),则输出:该字符(小写) 连续出现的次数。如果是非连续的字符&…...
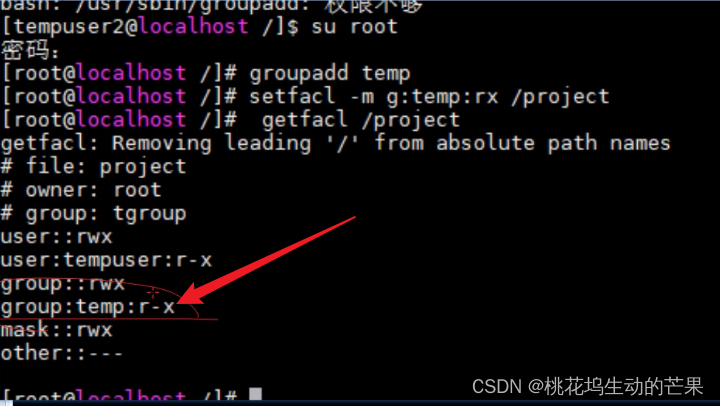
Linux进一步研究权限-----------ACL使用
一、使用情况 1.1、场景: 某个大公司,在一个部门,有一个经理和手下有两个员工,在操控一个Linux项目,项目又分为三期做,然而一期比较重要,经理带着员工做完了,公司就觉得技术难点已经做完攻克了࿰…...

剪辑视频调色软件有哪些 剪辑视频软件哪个最好 剪辑视频怎么学 剪辑视频的方法和步骤 会声会影2024 会声会影视频制作教程
看了很多调色教程,背了一堆调色参数,可最终还是调不出理想的效果。别再怀疑自己了,不是你的剪辑技术不行,而是剪辑软件没选对。只要掌握了最基本的调色原理,一款适合自己的视频剪辑软件是很容易出片的。 有关剪辑视频…...
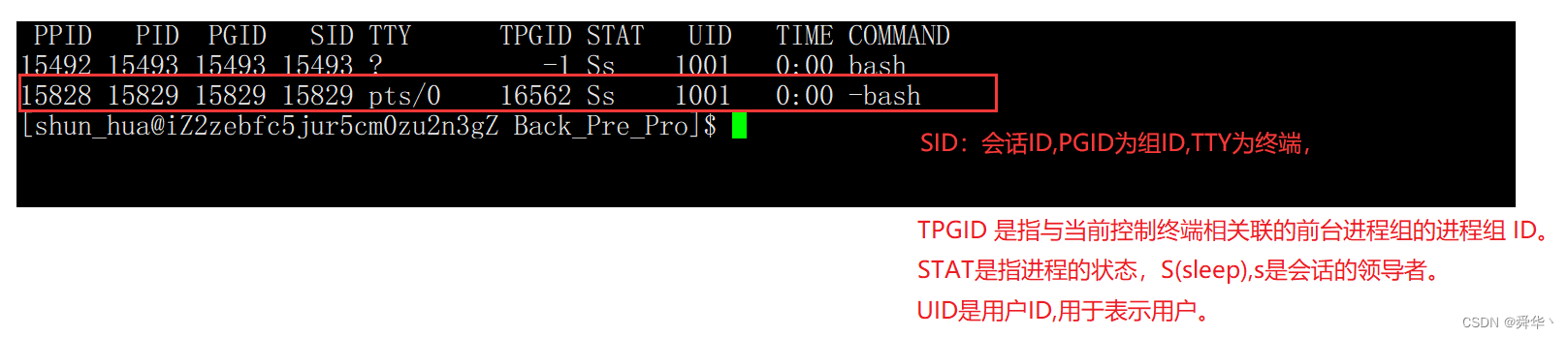
【Linux进阶之路】Socket —— “UDP“ “TCP“
文章目录 一、再识网络1. 端口号2. 网络字节序列3.TCP 与 UDP 二、套接字1.sockaddr结构2.UDP1.server端1.1 构造函数1.2 Init1.3 Run 2.客户端1.Linux2.Windows 3.TCP1. 基本接口2. 客户端3. 服务端1.版本12.版本23.版本34.版本4 三、守护进程尾序 一、再识网络 1. 端口号 在…...

一些用 GPT 翻译的计算机科学/人工智能 PDF 讲义
3D成像.pdf3D成像技术.pdf3D点云分析.pdfAAAI 2019 笔记.pdfCMU 10.708 概率图模型讲义.pdfCMU 15-312 编程语言基础讲义.pdfCMU 15-411 编译器设计讲义.pdfCMU 15-819 同伦类型论讲义.pdfCMU 15-819O 程序分析讲义.pdfCUNY CSci335 软件设计与分析 3 讲义.pdfDixie IT4500 信息…...
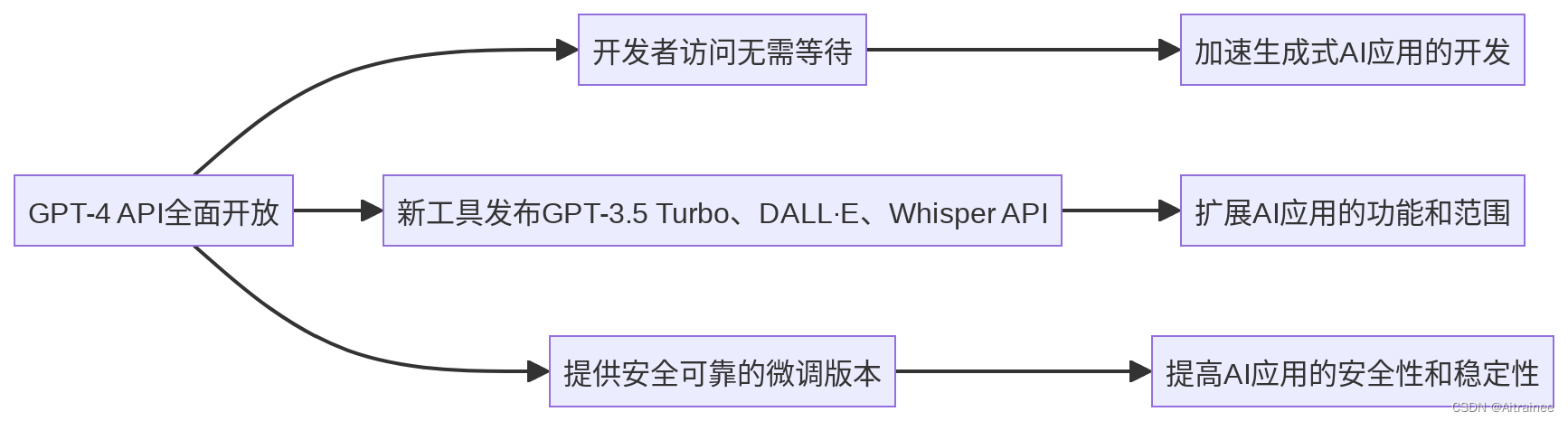
重大更新:GPT-4 API 现全面向公众开放!
重大更新:GPT-4 API 现全面向公众开放! 在 AIGC(人工智能生成内容)领域内,我们一直致力于跟踪和分析如 OpenAI、百度文心一言等大型语言模型(LLM)的进展及其在实际应用中的落地情况。我们还专注…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...
