【Docker】免费使用的腾讯云容器镜像服务

需要云服务器等云产品来学习Linux可以移步/-->腾讯云<--/官网,轻量型云服务器低至112元/年,新用户首次下单享超低折扣。
目录
1、设置密码
2、登录实例(sudo docker login xxxxxx)
3、新建命名空间(每个命名空间存放一组镜像仓库)
4、创建镜像仓库
5、传镜像、拉镜像
腾讯云容器镜像服务个人版免费,可以当做自己的docker仓库。
1、设置密码
进入控制台,搜索容器服务:
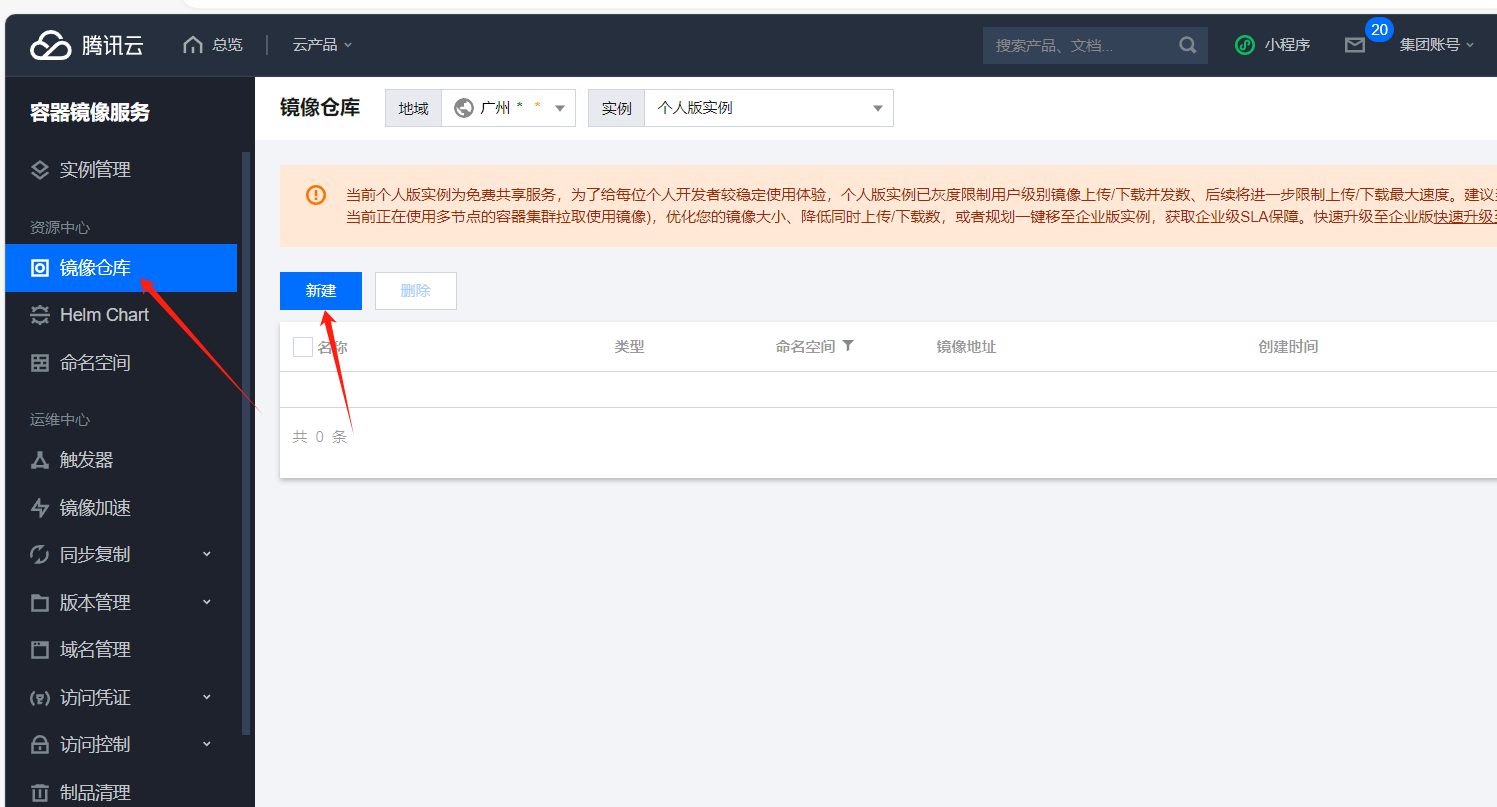
2、登录实例(sudo docker login xxxxxx)
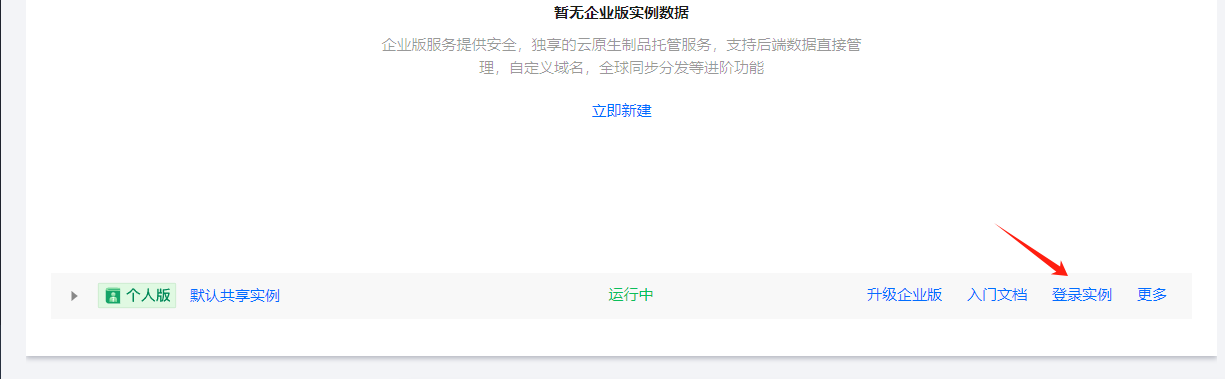
3、新建命名空间(每个命名空间存放一组镜像仓库)

4、创建镜像仓库


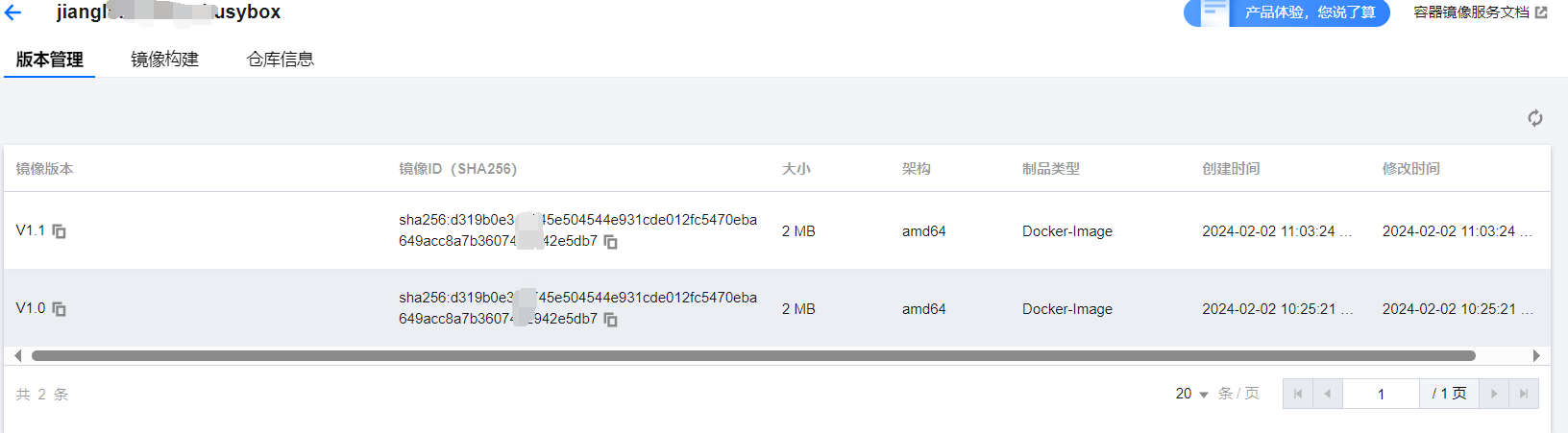
5、传镜像、拉镜像
sudo docker login ccr.ccs.tencentyun.com --username=xxxxxxxxxxxxxxx
sudo docker tag busybox:1.36 ccr.ccs.tencentyun.com/jianglingyu/my_busybox:V1.0 # 打标签
sudo docker push ccr.ccs.tencentyun.com/jianglingyu/my_busybox:V1.0 # 推送
sudo docker pull ccr.ccs.tencentyun.com/jianglingyu/my_busybox:V1.0 # 拉取
sudo docker logout ccr.ccs.tencentyun.com
相关文章:

【Docker】免费使用的腾讯云容器镜像服务
需要云服务器等云产品来学习Linux可以移步/-->腾讯云<--/官网,轻量型云服务器低至112元/年,新用户首次下单享超低折扣。 目录 1、设置密码 2、登录实例(sudo docker login xxxxxx) 3、新建命名空间(每个命名空…...

如何让qml使用opengl es
要让 QML 使用 OpenGL ES,您需要确保项目配置正确,并在应用程序中使用 QSurfaceFormat 来设置 OpenGL ES 渲染。 以下是一些步骤来配置 QML 使用 OpenGL ES: 1、项目配置:在您的项目配置文件(例如 .pro 文件…...

金航标电子位于广西柳州鹿寨县天线生产基地于大年正月初九开工了!!
金航标电子位于广西柳州鹿寨县天线生产基地于大年正月初九开工了!!!金航标kinghelm( http://www.kinghelm.com.cn )总部位于中国深圳市,兼顾技术、成本、管理、效率和可持续发展。东莞塘厦实验室全电波暗…...

FlinkCDC详解
1、FlinkCDC是什么 1.1 CDC是什么 CDC是Chanage Data Capture(数据变更捕获)的简称。其核心原理就是监测并捕获数据库的变动(例如增删改),将这些变更按照发生顺序捕获,将捕获到的数据,写入数据…...

力扣代码学习日记六
Problem: 66. 加一 思路 给定一个由 整数 组成的 非空 数组所表示的非负整数,在该数的基础上加一。 最高位数字存放在数组的首位, 数组中每个元素只存储单个数字。 你可以假设除了整数 0 之外,这个整数不会以零开头。 示例 1: 输…...

「Python系列」Python标准库
文章目录 一、 os 模块:文件和目录操作二、 sys 模块:与Python解释器交互三、 datetime 模块:日期和时间处理四、 json 模块:处理JSON数据五、 re 模块:正则表达式六、 time模块1. 获取当前时间2. 延迟执行(…...
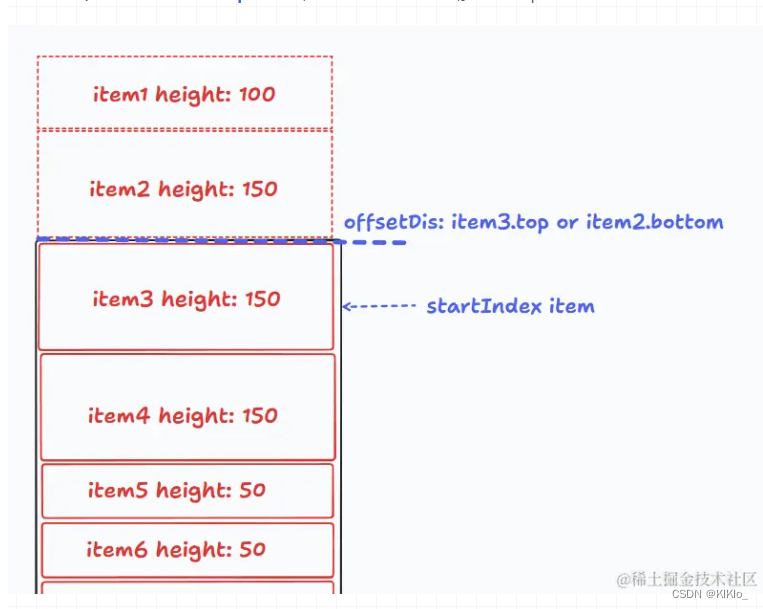
虚拟列表【vue】等高虚拟列表/非等高虚拟列表
文章目录 1、等高虚拟列表2、非等高虚拟列表 1、等高虚拟列表 参考文章1 参考文章2 <!-- eslint-disable vue/multi-word-component-names --> <template><divclass"waterfall-wrapper"ref"waterfallWrapperRef"scroll"handleScro…...
【MySQL】如何理解索引(高频面试点)
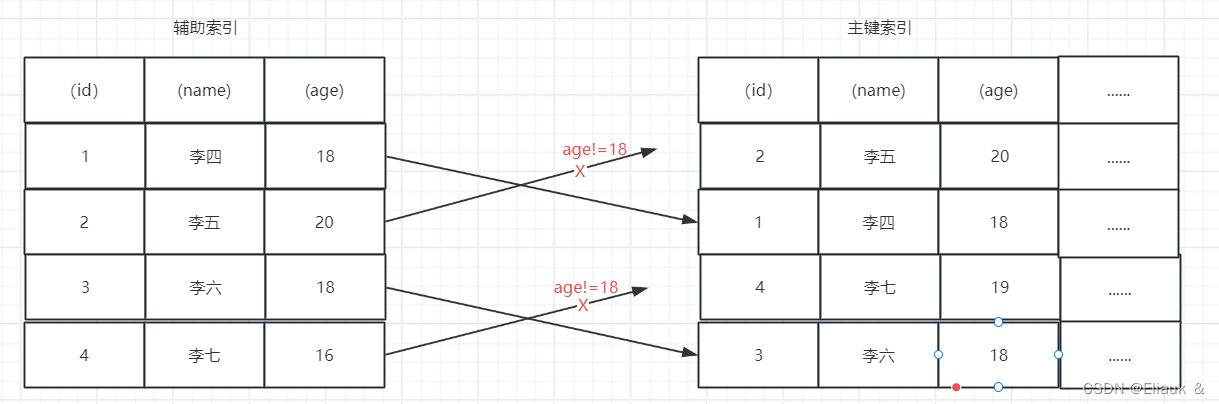
一、前言 首先这个博客会介绍一些关于MySQL中索引的基本内容以及一些基本的语法,当然里面也会有些常见的面试题的解答。 二、关于索引 1、概念 索引是一种能够帮助MySQL高效的去磁盘检索数据的一种数据结构。在MySQL的Innodb存储引擎中呢,采用的是B树的…...
:S32K3xx如何产生中心对称三相六路波形)
NXP实战笔记(四):S32K3xx如何产生中心对称三相六路波形
目录 1、概述 1.1、理论基础 2、RTD实现 2.1、Emios时基配置 2.1.1、EmiosMcl 2.1.2、EmiosCommon 2.2、Emios PWM配置 2.3、TRGMUX 2.4、LCU 2.5、外设信号配置 3、代码实现 4、测试结果 1、概述 电机控制中需要产生三相六路SVPWM进行占空比与周期调制,怎么通过RT…...

关于uniapp H5应用无法在触摸屏正常显示的处理办法
关于uniapp H5应用无法在触摸屏正常显示的处理办法 1、问题2、处理3、建议 1、问题 前几天, 客户反馈在安卓触摸大屏上无法正确打开web系统(uni-app vue3开发的h5 应用),有些页面显示不出内容。该应用在 pc 端和手机端都可以正常…...

Stable Diffusion 3 发布,AI生图效果,再次到达全新里程碑!
AI生图效果,再次到达全新里程碑! Prompt:Epic anime artwork of a wizard atop a mountain at night casting a cosmic spell into the dark sky that says "Stable Diffusion 3" made out of colorful energy 提示(意译…...
?)
单例模式怎样实现单例(独例)?
在类定义中加入私有属性 __init__flag Ture,在随后的初始化处理中,判断该属性为真时进行相应的初始化操作,否则,跳过相应的初始化操作。这个机制,保证在进行后续的调用时,不再占用额外的内存开销。 当然了,…...
MySQL——基础内容
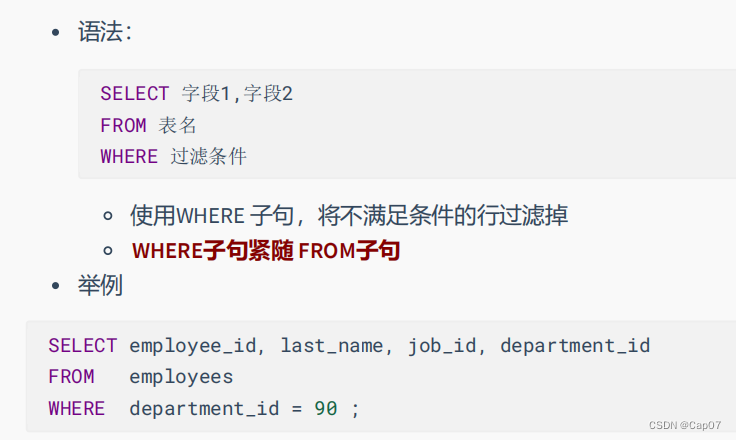
目录 第01章_数据库概述 关系型数据库(RDBMS)——表、关系模型 非关系型数据库(非RDBMS) 表、记录、字段 表的关联关系 一对一关联 一对多关系 多对多 自我引用 第02章_MySQL环境搭建 登录命令 常用命令 show databases; create database use 数据库名 show tables 第03章…...
node 之 初步认识
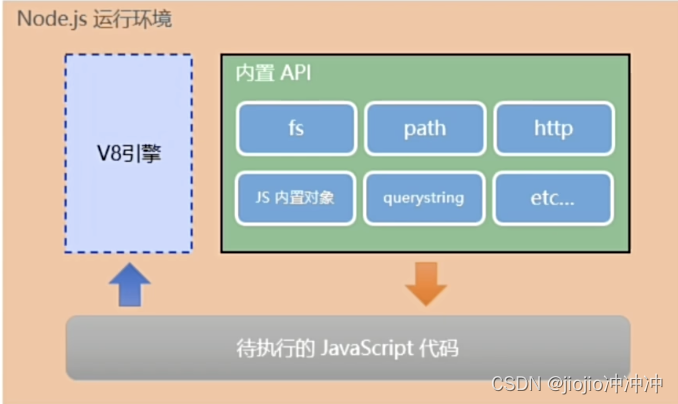
思考:为什么JavaScript可以在浏览器中被执行 代执行的js代码——JavaScript解析引擎 不同的浏览器使用不同的JavaScript解析引擎 Chrome 浏览器 》 V8 Firefox浏览器 》OdinMonkey(奥丁猴) Safri浏览器 》JSCore IE浏览器 》Chakra(查克拉) e…...
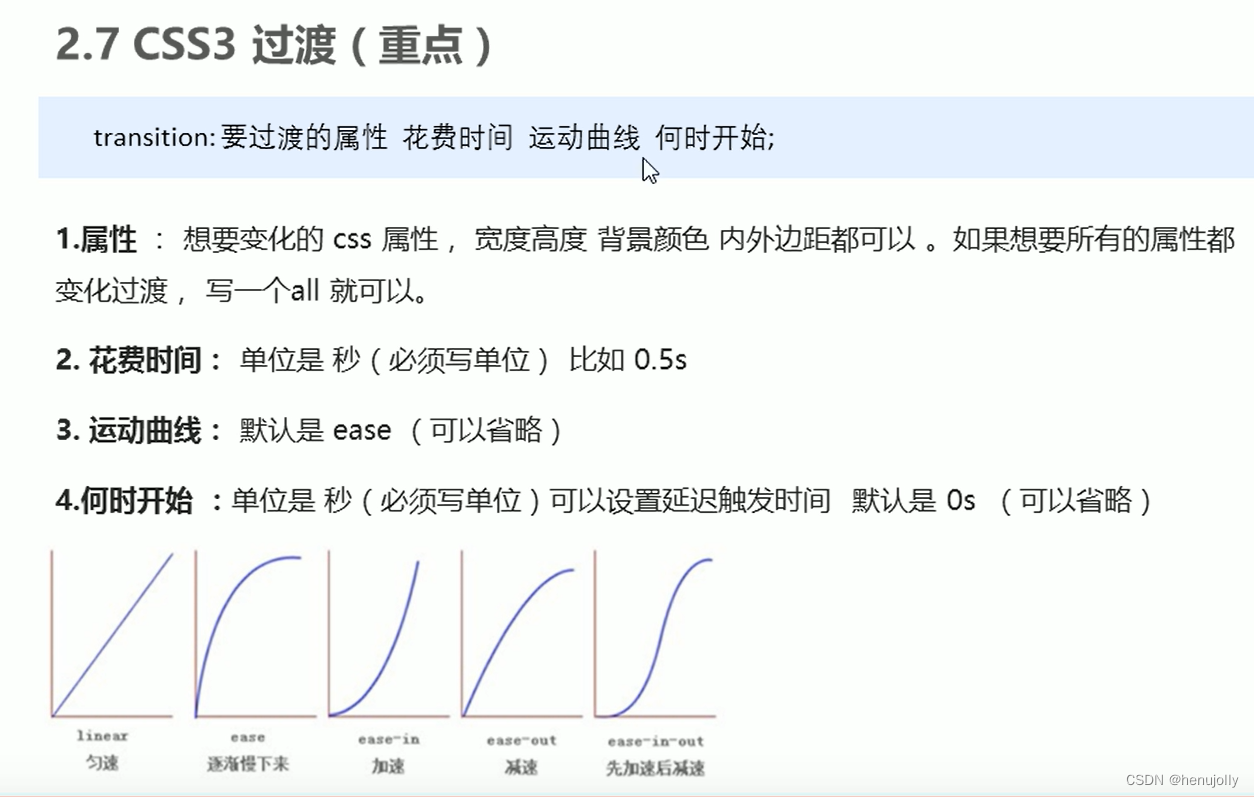
css复习
盒模型相关: border:1px solid red (没有顺序) 单元格的border会发生重叠,如果不想要重叠设置 border-collapse:collapse (表示相邻边框合并在一起) padding padding影响盒子大小的好处使用 margin应用: 行内或行内块元素水…...
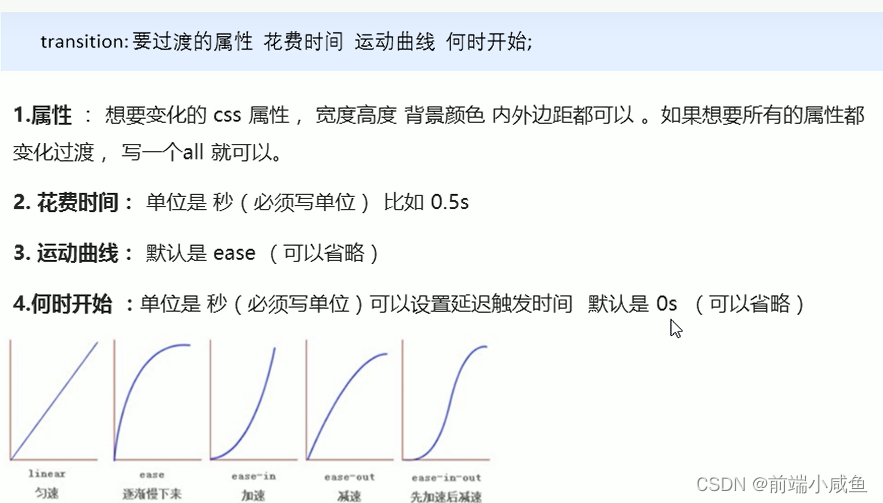
HTML5和CSS3提高
一、HTML5的新特性 增加了一些新的标签,新的表单,新的表单属性,IE9以上版本的浏览器才支持 注意: 这些语义化标准主要针对搜索引擎的 新标签可以使用多次 在IE9中需要把这些元素转化为块级元素 新增的多媒体标签 主要包含两个…...

感受2024生物发酵展示会-明章机械
参展企业介绍 温州明章机械有限公司是一家专业从事搅拌传动装置机械密封,减速机,机架,联轴器及相关配件。设计、开发及生产的服务型高新技术企业公司,座落于浙江省温州市瓯海区娄桥镇高新工业园区豪新路42号,交通位置…...
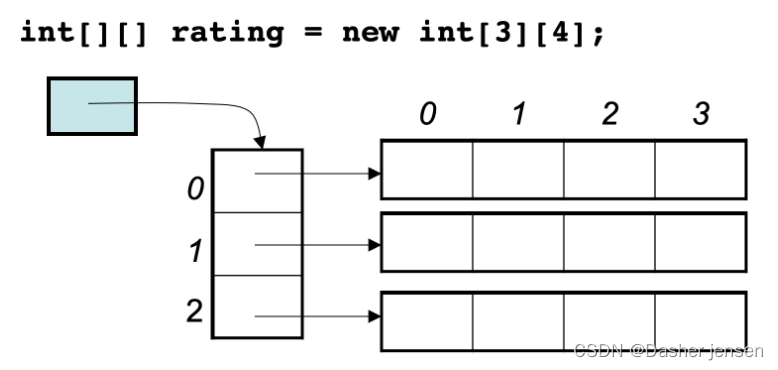
算法打卡day1|数组篇|Leetcode 704.二分查找、27.移除元素
数组理论基础 数组是存放在连续内存空间上的相同类型数据的集合,可以方便的通过下标索引的方式获取到下标下对应的数据。 1.数组下标都是从0开始的。 2.数组内存空间的地址是连续的。 正是因为数组的在内存空间的地址是连续的,所以我们在删除或者增添…...

什么是高阶组件
高阶组件(HOC)是 React 中用于复用组件逻辑的一种高级技巧。简单来说,高阶组件就是一个函数,该函数接受一个组件作为参数,并返回一个新的组件。这个新的组件会使用你传给它的组件作为子组件。 高阶组件并不是真的组件…...

python实现裂区试验方差分析
方差分析(Analysis of Variance,ANOVA)是一种统计方法,用于比较三个或三个以上组别的平均值是否存在显著差异。它通过比较组内变异和组间变异的大小来判断组别间的平均值是否有显著差异。 方差分析通常用于以下情况: …...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...
