【蓝桥备赛】字串简写
字串简写



数据范围 字符串的长度为5*10的五次方,on方时间复杂度会很大。
才用动态规划的思想,dp[i]以i开头的的可能性,因为长度必须大于等于k,当i小于k的时候,如果等于第一个字符,s1时,dp[i]=dp[i-1]+1,如果不等于dp[i]=dp[i-1];
当i大于k-1时,如果以第二个字符结尾的,ans就需要加上dp[i-k+1]
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
ll dp[N];
int main()
{int k;cin >> k;string s;cin >> s;char s1, s2;cin >> s1 >> s2;int res = 0;for (int i = 1; i < k; i++){dp[i] = dp[i - 1] + (s[i] == s1 ? 1 : 0);}for (int i = k; i < s.length(); i++){dp[i] = dp[i - 1] + (s[i] == s1 ? 1 : 0);if (s[i] == s2){res += dp[i - k];}}cout << res;
}
相关文章:

【蓝桥备赛】字串简写
字串简写 数据范围 字符串的长度为5*10的五次方,on方时间复杂度会很大。 才用动态规划的思想,dp[i]以i开头的的可能性,因为长度必须大于等于k,当i小于k的时候,如果等于第一个字符,s1时,dp[…...
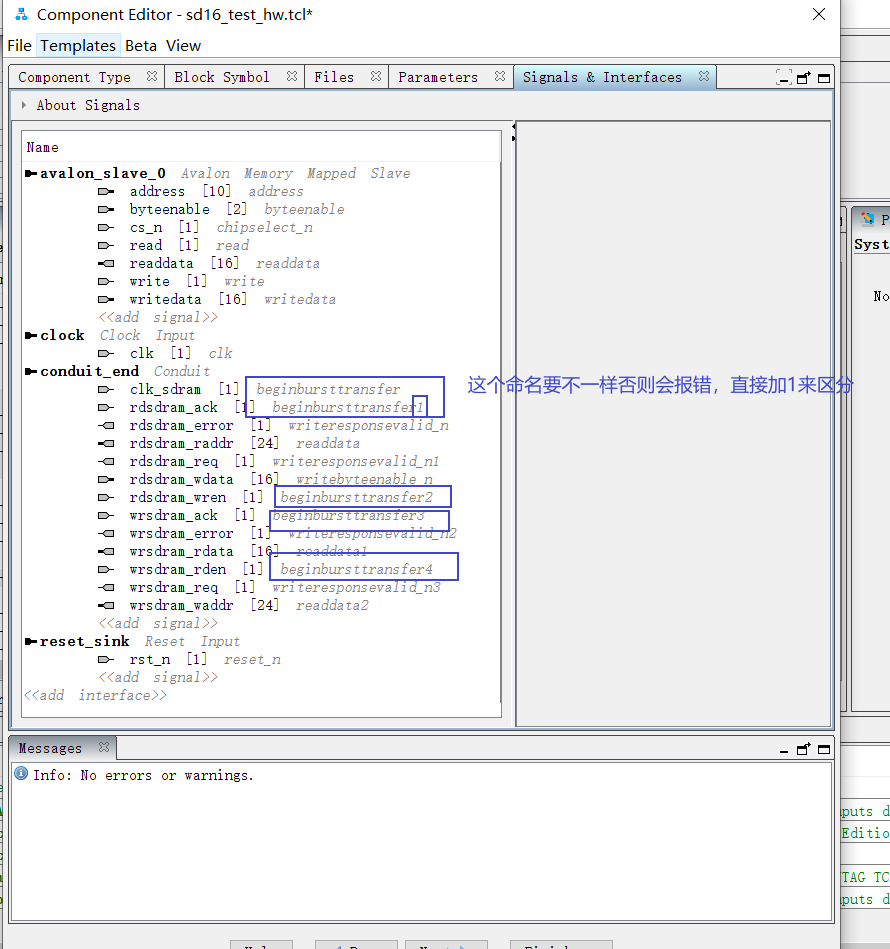
nios ii开发随笔
错误一: d:/intelfpga/17.1/nios2eds/bin/gnu/h-x86_64-mingw32/bin/../lib/gcc/nios2-elf/5.3.0/../../../../../H-x86_64-mingw32/nios2-elf/bin/ld.exe: test.elf section .text will not fit in region ram_oc_xzs d:/intelfpga/17.1/nios2eds/bin/gnu/h-x86_6…...

SpringBoot项目嵌入RabbitMQ
在Spring Boot中嵌入RabbitMQ可以通过添加相应的依赖来完成。首先需要在pom.xml文件中引入spring-boot-starter-amqp依赖: <dependency> <groupId>org.springframework.boot</groupId> <artifactId>spring-boot-starter-amqp</a…...
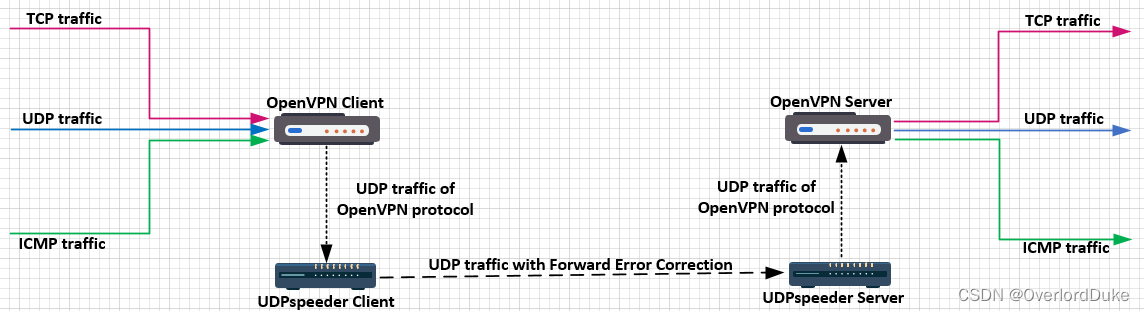
提升网络质量:UDPspeeder 实现网络优化与提速
提升网络质量:UDPspeeder 实现网络优化与提速 背景与意义原理与功能使用方法未来展望相关链接服务 在当今高度互联的网络环境下,网络质量的优化和提速对于用户体验至关重要。针对高延迟和丢包率较高的网络链路,UDPspeeder 提供了一种前向纠错…...

为什么前端开发变得越来越复杂了?这可能是我们的错
前端训练营:1v1私教,终身辅导计划,帮你拿到满意的 offer。 已帮助数百位同学拿到了中大厂 offer。欢迎来撩~~~~~~~~ Hello,大家好,我是 Sunday。 最近有很多同学来问我:“Sunday 老师,前端学起…...
VR系统的开发流程
虚拟现实(Virtual Reality,VR)系统是一种通过计算机技术模拟出的具有三维视角和交互性的虚拟环境,使用户能够沉浸在其中并与虚拟环境进行交互。这种技术通常利用头戴式显示器和手柄等设备,使用户能够感觉到仿佛身临其境…...
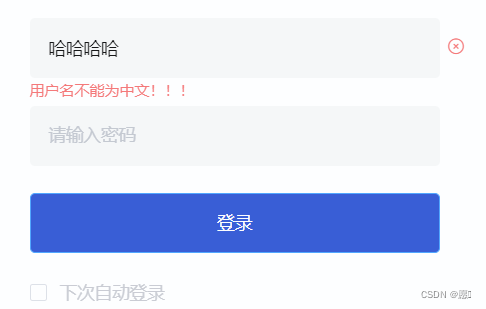
前端输入框校验限制不能输入中文
一般我们在做表单的时候都会有表单校验,通常都是用element提供的表单验证的功能,只需要通过 rules 属性传入约定的验证规则,如下面这样 rules: {userName: [{validator: checkUsername,trigger: "blur",},{ validator: this.checkData, trigge…...
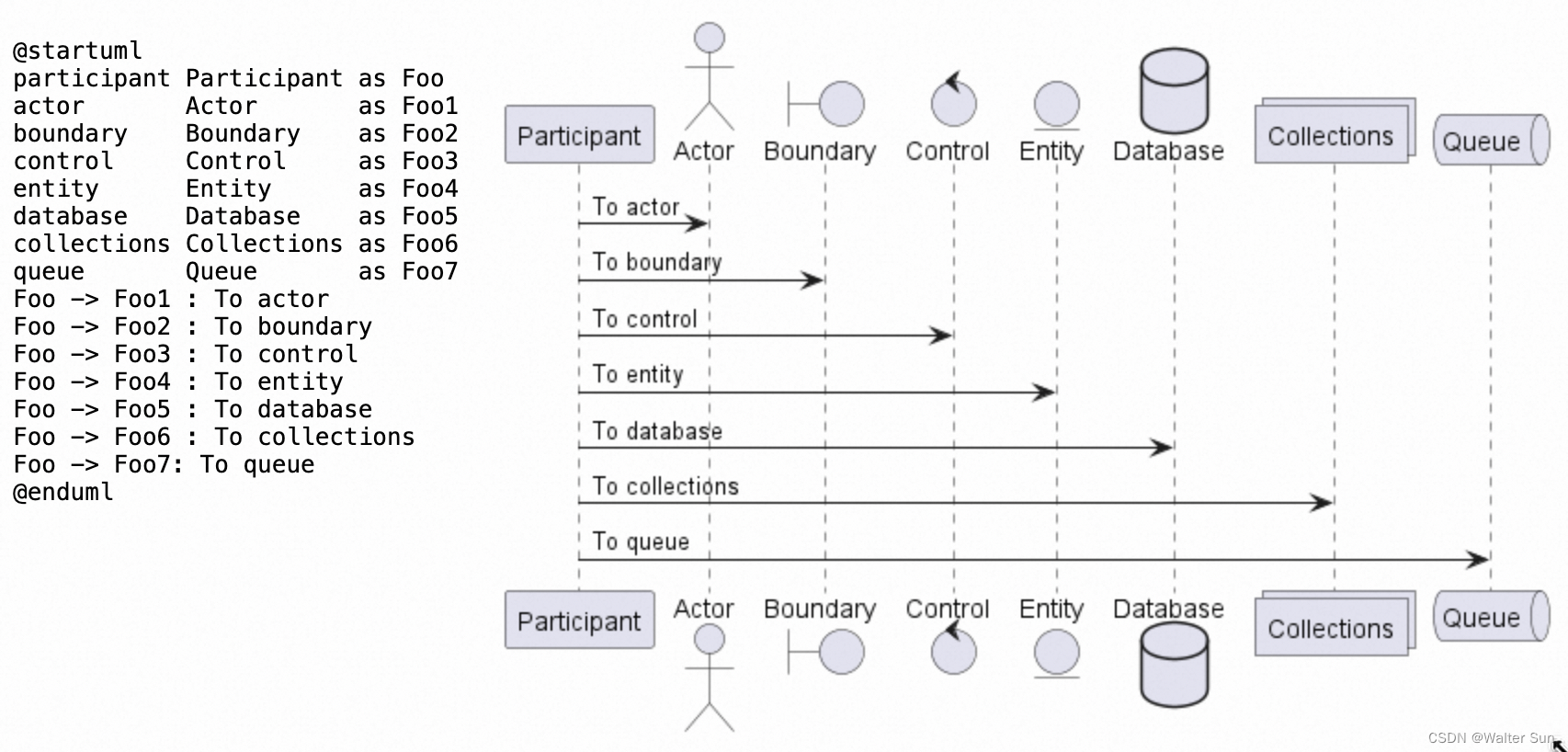
强大的文本绘图——PlantUML
PlantUML是一款开源工具,它允许用户通过简单的文本描述来创建UML图(统一建模语言图)。这种方法可以快速地绘制类图、用例图、序列图、状态图、活动图、组件图和部署图等UML图表。PlantUML使用一种领域特定语言(DSL)&am…...

ES相关问题
在Elasticsearch(ES)集群中,节点根据其配置和角色可以分为以下几种主要类型: Master Node(主节点): 主节点负责管理整个集群的元数据,如索引的创建、删除、分片分配等。它维护着集群…...

基于Linux直接安装的Nginx版本升级方法
引言 随着版本的迭代和漏洞的发现,Nginx作为一款软件避免不了打补丁的命运。 以下基于Linux直接安装的Nginx版本升级。 以下操作均在本地虚拟机中操作验证,请验证后再线上操作。基于centos7测试。 前置资源 获取nginx的最新源码版本网址:…...

探索设计模式的魅力:状态模式揭秘-如何优雅地处理复杂状态转换
🌈 个人主页:danci_ 🔥 系列专栏:《设计模式》 💪🏻 制定明确可量化的目标,并且坚持默默的做事。 探索设计模式的魅力:状态模式揭秘-如何优雅地处理复杂状态转换 文章目录 一、案例…...
)
力扣hot100题解(python版10-12题)
哎- -最近本来就没时间写算法 这算法怎么还这么难。。。 10、和为 K 的子数组 给你一个整数数组 nums 和一个整数 k ,请你统计并返回 该数组中和为 k 的子数组的个数 。 子数组是数组中元素的连续非空序列。 示例 1: 输入:nums [1,1,1]…...

【算法】复杂度分析
第一章、如何分析代码的执行效率和资源消耗 我们知道,数据结构和算法解决的是“快”和“省”的问题,也就是如何让代码运行得更快,一级如何让代码更节省计算机的存储空间。因此,执行效率是评价算法好坏的一个非常重要的指标。那么&…...

车载电子测试学习内容
搜集了一些车载测试的学习内容,大家可以参考。...
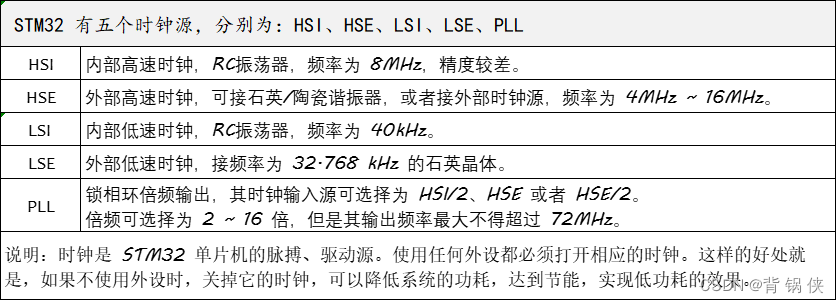
STM32F103x 的时钟源
AHB (Advanced High-performance Bus) 高速总线,用来接高速外设的。 APB (Advanced Peripheral Bus) 低速总线,用来接低速外设的,包含APB1 和 APB2。 APB1:上面连接的是低速外设,包括电源接口、备份接口、 CAN 、 US…...
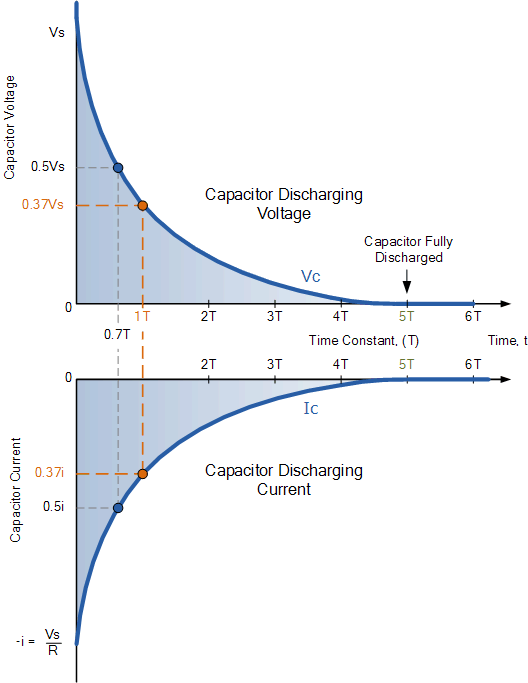
【电路笔记】-RC放电电路
RC放电电路 文章目录 RC放电电路1、概述2、RC放电电路3、RC放电电路示例当电压源从完全充电的 RC 电路中移除时,电容器 C 将通过电阻 R 放电。 1、概述 RC 放电电路利用电阻器-电容器组合的固有 RC 时间常数以指数衰减率对电容器进行放电。 在之前的 RC 充电电路教程中,我们…...

【C++STL】STL容器详解
创作不易,本篇文章如果帮助到了你,还请点赞 关注支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 🔥c系列专栏:C/C零基础到精通 🔥 给大…...
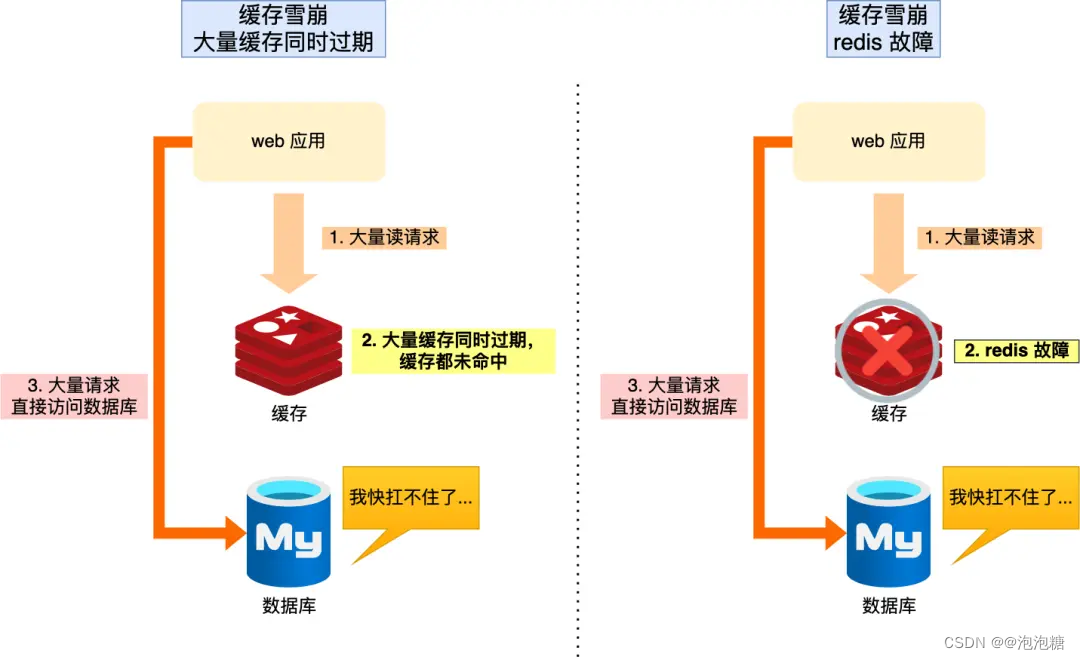
缓存篇—缓存雪崩
什么是缓存雪崩 通常我们为了保证缓存中的数据与数据库中的数据一致性,会给 Redis 里的数据设置过期时间,当缓存数据过期后,用户访问的数据如果不在缓存里,业务系统需要重新生成缓存,因此就会访问数据库,并…...
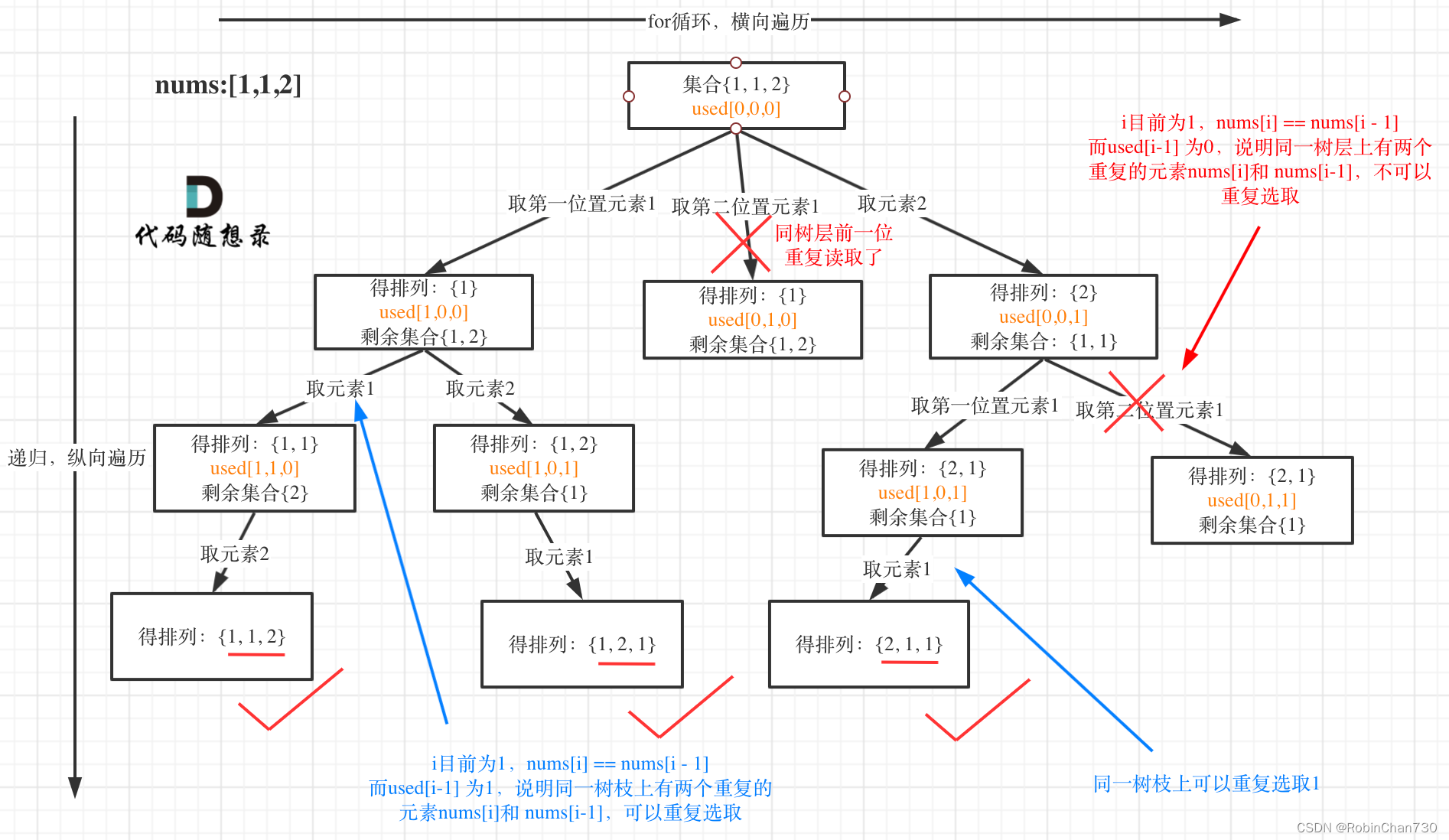
力扣日记2.22-【回溯算法篇】47. 全排列 II
力扣日记:【回溯算法篇】47. 全排列 II 日期:2023.2.22 参考:代码随想录、力扣 47. 全排列 II 题目描述 难度:中等 给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。 示例 1: 输…...

如何理解三大微分中值定理
文章看原文,自己写的只是备份 高等数学强化2:一元函数微分学 中值定理 极值点 拐点_一元函数中值定理-CSDN博客 高等数学强化3:一元函数积分学 P积分-CSDN博客 高等数学强化3:定积分几何应用-CSDN博客...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...

Linux-进程间的通信
1、IPC: Inter Process Communication(进程间通信): 由于每个进程在操作系统中有独立的地址空间,它们不能像线程那样直接访问彼此的内存,所以必须通过某种方式进行通信。 常见的 IPC 方式包括&#…...

js 设置3秒后执行
如何在JavaScript中延迟3秒执行操作 在JavaScript中,要设置一个操作在指定延迟后(例如3秒)执行,可以使用 setTimeout 函数。setTimeout 是JavaScript的核心计时器方法,它接受两个参数: 要执行的函数&…...

免费批量Markdown转Word工具
免费批量Markdown转Word工具 一款简单易用的批量Markdown文档转换工具,支持将多个Markdown文件一键转换为Word文档。完全免费,无需安装,解压即用! 官方网站 访问官方展示页面了解更多信息:http://mutou888.com/pro…...

day51 python CBAM注意力
目录 一、CBAM 模块简介 二、CBAM 模块的实现 (一)通道注意力模块 (二)空间注意力模块 (三)CBAM 模块的组合 三、CBAM 模块的特性 四、CBAM 模块在 CNN 中的应用 一、CBAM 模块简介 在之前的探索中…...

【Axure高保真原型】图片列表添加和删除图片
今天和大家分享图片列表添加和删除图片的原型模板,效果包括: 点击图片列表的加号可以显示图片选择器,选择里面的图片; 选择图片后点击添加按钮,可以将该图片添加到图片列表; 鼠标移入图片列表的图片&…...
