迭代、递归、尾递归实现斐波那契数列的第n项
1.什么是斐波那契数列:
斐波那契数,亦称之为斐波那契数列(意大利语: Successione di Fibonacci),又称黄金分割数列、费波那西数列、费波拿契数、费氏数列和兔子数列,指的是这样一个数列:0、1、1、2、3、5、8、13、21、……在数学上,斐波纳契数列以如下被以递归的方法定义:F0=0,F1=1,Fn=F(n-1)+F(n-2)(n>=2,n∈N*),用文字来说,就是斐波那契数列列由 0 和 1 开始,之后的斐波那契数列系数就由之前的两数相加。
学习内容:
这里我们针对以1,1,为前两项的斐波那契数列,(1,1,2,3,5,8,13……)某一项即为前两项的和,这里介绍三种方法来实现它
1.迭代法:
long fac(int x)//迭代
{int i;int a = 1;int b = 1;int c = 0;for (i = 0; i < x - 2; i++){c = a + b;a = b;b = c;}return c;
}
int main()
{int a;scanf("%d", &a);printf("%d", fac(a));return 0;
}我们先将前两个1储存在a,b中,在第一个循环中,c接收了a和b的和,再让a接收b的值,b接收c的值。如此循环往复(x-2)次,最终c的值即为f(x).
在这过程中,a,b值的更新是为了令a=f(x-2),b=f(x-1).所需循环次数由下得出:
求第三项:只需进行一次循环,即进行一次相加
求第四项:进行两次循环,即进行两次相加
求第五项:进行三次循环,即进行三次相加
……
不难看出,求第x项时,就需要进行x-2次循环了
2.线性递归法
int fac(int x)//线性递归
{if (x == 1 || x == 2)return 1;elsereturn fac(x - 2) + fac(x - 1);此种方法很简单,就是根据数学定义按部就班:F1=1,F2=1,Fn=F(n-1)+F(n-2)(n>=3,n∈N*)
3.尾递归
int fun(int n,int a,int b)
{if(n<3)return b;else
return fun(n-1,b,a+b);
}
int main()
{
printf("%d",fun(5,1,1));
return 0;
}我们来验证一下fun函数的功能,首先传参时必须保证形参a,b都接收1,传递(5,1,1,),过程如下:
fun(4,1,2)
fun(3,2,3)
fun(2,3,5)
当n-1=2时,函数就会返回第三形参——5
相关文章:

迭代、递归、尾递归实现斐波那契数列的第n项
1.什么是斐波那契数列: 斐波那契数,亦称之为斐波那契数列(意大利语: Successione di Fibonacci),又称黄金分割数列、费波那西数列、费波拿契数、费氏数列和兔子数列,指的是这样一个数列:0、1、…...

vulnhub靶场之driftingblues-1
一.环境搭建 1.靶场描述 get flags difficulty: easy about vm: tested and exported from virtualbox. dhcp and nested vtx/amdv enabled. you can contact me by email (it should be on my profile) for troubleshooting or questions. 2.靶场下载 https://www.vulnhub.…...
NGINX服务器配置实现加密的WebSocket连接WSS协议
一、背景 最近在做小程序开发,需要在nginx中配置websocket加密模式,即wss。初次配置wss时,踩了两个小时的坑,本文将踩坑过程分享给大家,有需要用到的伙伴可以直接copy即可实现,节省宝贵时间。 二、WebSo…...
5个免费文章神器,用来改写文章太方便了
在当今信息爆炸的时代,内容创作和编辑是网络世界中至关重要的环节。然而,有时候我们可能会遇到一些内容需要进行改写或者重组的情况。为了提高效率,让这一过程更加顺畅,我们可以借助一些免费的文章神器来帮助我们完成这一任务。下…...
详细教程!VMware Workstation Pro16 安装 + 创建 win7 虚拟机!
嚯嚯嚯,很多宝子都想拥有自己不同的操作系统环境,用于学习或项目搭建。买服务器费钱,虚拟机则成为了一个很好的选择。本文详细介绍VMware Workstation Pro 16安装及win7虚拟机创建,保姆级教程奉上! 一、准备工作 VMw…...
Python文件和异常(二)
目录 三、异常 (一)处理 ZeroDivisionError 异常 (二)使用 try-except 代码块 (三)使用异常避免崩溃 (四)else 代码块 (五)处理 FileNotFoundError 异常…...
大模型+影像:智能手机“上春山”
这个春节假期,一首《上春山》火了。吃瓜群众热热闹闹学了一个假期的“春山学”,了解了抢占C位的各种技巧。 假期过去,开工大吉,手机行业开始抢占今年的C位。那么问题来了,今年智能手机最大的机会点在哪里?答…...

8-pytorch-损失函数与反向传播
b站小土堆pytorch教程学习笔记 根据loss更新模型参数 1.计算实际输出与目标之间的差距 2.为我们更新输出提供一定的依据(反向传播) 1 MSEloss import torch from torch.nn import L1Loss from torch import nninputstorch.tensor([1,2,3],dtypetorch.fl…...
-数据库连接池的配置与优化)
MySQL高级特性篇(8)-数据库连接池的配置与优化
MySQL数据库连接池的配置与优化 MySQL数据库是当前最流行的关系型数据库管理系统之一,高效的数据库连接池配置与优化是提高数据库性能和并发性能的重要手段。本文将介绍MySQL数据库连接池的配置与优化,并提供详细示例。 1. 连接池的作用与优势 数据库…...
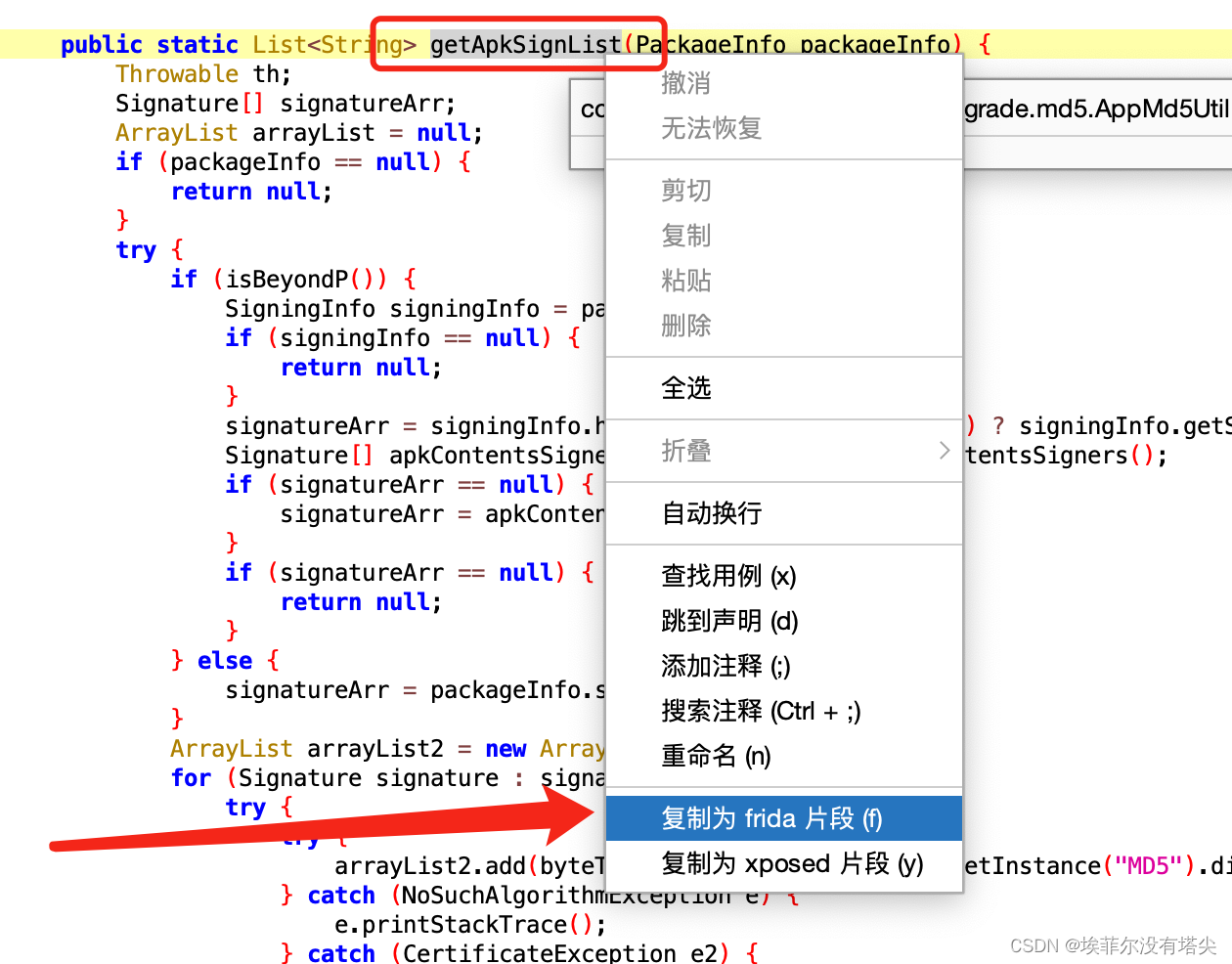
mac下使用jadx反编译工具
直接执行步骤: 1.创建 jadx目录 mkdir jadx2.将存储库克隆到目录 git clone https://github.com/skylot/jadx.git 3. 进入 jadx目录 cd jadx 4.执行编译 等待片刻 ./gradlew dist出现这个就代表安装好了。 5.最后找到 jadx-gui 可执行文件,双击两下…...

分布式一致性软件-zookeeper
在我们进行软件开发过程中,为了实现某个功能可能借助多个软件,如存储数据的数据库软件:MySQL,Redis;消息中间件:rocketMq,kafka等。那么在分布式系统中,如果想实现数据一致性&#x…...

企业计算机服务器中了babyk勒索病毒怎么办?Babyk勒索病毒解密数据恢复
随着网络技术的应用与普及,越来越多的企业采用了数字化办公模式,数字化办公模式可以为企业提供强有力的数据支撑,可以为企业的发展方向与产品业务调整做好基础工作。但网络是一把双刃剑,在为企业提供便利的同时,也为企…...
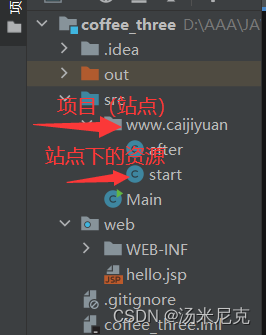
板块一 Servlet编程:第五节 Cookie对象全解 来自【汤米尼克的JAVAEE全套教程专栏】
板块一 Servlet编程:第五节 Cookie对象全解 一、什么是CookieCookie的源码 二、Cookie的具体操作(1)创建Cookie(2)获取Cookie(3)设置Cookie的到期时间(4)设置Cookie的路径…...

自动驾驶---Motion Planning之Path Boundary
1 背景 在上文《自动驾驶---Motion Planning之LaneChange》中,笔者提到过两种LaneChange的思路,这里再简单回顾一下:(1)利用Routing和周围环境的信息,决定是否进行换道的决策;(2)采用的博弈思想(蒙特卡洛树搜索---MCTS)决定是否进行换道的决策。不管是变道,避让还是…...

Leetcode 3048. Earliest Second to Mark Indices I
Leetcode 3048. Earliest Second to Mark Indices I 1. 解题思路2. 代码实现 题目链接:3048. Earliest Second to Mark Indices I 1. 解题思路 这一题的话基础的思路就是二分法查找最小的可以将所有的数字都mark上的最小位置。 因此,这里的问题就会变…...
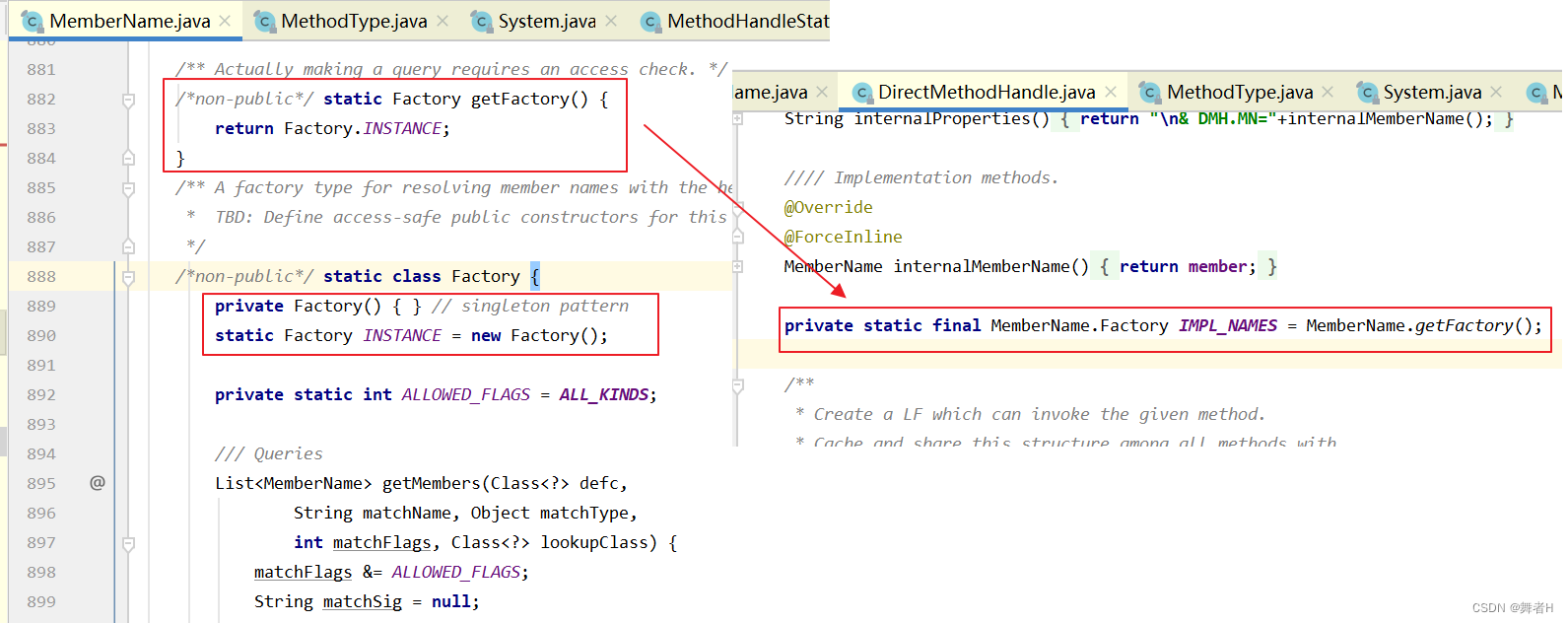
从源码学习单例模式
单例模式 单例模式是一种设计模式,常用于确保一个类只有一个实例,并提供一个全局访问点。这意味着无论在程序的哪个地方,只能创建一个该类的实例,而不会出现多个相同实例的情况。 在单例模式中,常用的实现方式包括懒汉…...

axios介绍和使用
1. Axios是什么 Axios框架全称(ajax – I/O – system) Axios是一个基于Promise的JavaScript HTTP客户端,用于浏览器和Node.js环境。它可以发送HTTP请求并支持诸如请求和响应拦截、转换数据、取消请求以及自动转换JSON数据等功能。 Axios提…...

redis雪崩问题
Redis雪崩问题是指在Redis缓存系统中,由于某些原因导致大量缓存数据同时失效或过期,导致所有请求都直接访问数据库,从而引发数据库性能问题甚至宕机的情况。 造成Redis雪崩问题的原因主要有以下几个: 缓存数据同时失效ÿ…...

[SUCTF 2019]EasySQL1 题目分析与详解
一、题目介绍 1、题目来源: BUUCTF网站,网址:https://buuoj.cn/challenges 2、题目描述: 通过以上信息,拿到flag。 二、解题思路 首先打开靶机,尝试输入1查看回显,回显如图所示:…...
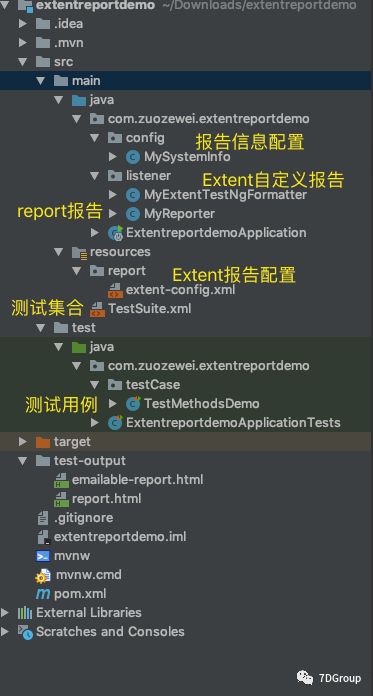
TestNG与ExtentReport单元测试导出报告文档
TestNG与ExtentReport集成 目录 1 通过实现ITestListener的方法添加Reporter log 1.1 MyTestListener设置 1.2 输出结果 2 TestNG与ExtentReporter集成 2.1 项目结构 2.2 MyExtentReportListener设置 2.3 单多Suite、Test组合测试 2.3.1 单Suite单Test 2.3…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
