蓝桥杯第1374题——锻造兵器
题目描述
小明一共有n块锻造石,第块锻造石的属性值为ai.
现在小明决定从这n块锻造石中任取两块来锻造兵器
通过周密计算,小明得出,只有当两块锻造石的属性值的差值等于C,兵器才能锻造成功
请你帮小明算算,他有多少种选取锻造石的方案可以使得锻造成功
输入描述
第一行包含两个整数n,C,其含义如题所述
接下来一行包含n个整数,分别表示a1,a2,··,an.
1 < N < 2 x 10^5,|ai| < 10^4,0 < C < 10^9
输出描述
输出共一行,包含一个整数,表示答案.
输入输出样例
6 3
8 4 5 7 7 4
5
解题思路
这个题是一道典型的双指针题,要控制快指针和慢指针所对应的数据之差为C。
首先,使用排序方法对输入数据进行排序是必要的。
然后快指针优先移动,直到快慢指针数据之差至少为C;接下来慢指针进行移动,如果不是C(就一定比C大)就往后移动,直到快慢指针之差至多为C。
到此就是一组快慢指针的移动,此时可以判断快慢指针数据之差是否为C,如果是,就对ans做更新。这题的关键是ans更新多少,我们思考后不难发现,按照题目提供的例子,两个7的石头可以与两个4的石头分别组成一组,这意味着组合数量是满足要求的两个数值的石头的个数乘积,那么我们只需要对快慢指针分别派生出一个新指针,分别向后步进进行计数即可。
下面给出代码:
import java.io.BufferedReader;
import java.io.FileReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.lang.reflect.Array;
import java.math.BigInteger;
import java.util.*;public class Main {public static void main(String[] args) throws IOException {Scanner sc = new Scanner(System.in);BufferedReader in = new BufferedReader(new InputStreamReader(System.in));String[] temp = in.readLine().split(" ");int n = Integer.parseInt(temp[0]);int c = Integer.parseInt(temp[1]);temp = in.readLine().split(" ");int[] data = new int[n];for (int i = 0; i < n; i++) {data[i] = Integer.parseInt(temp[i]);}Arrays.sort(data);int slow = 0, fast = 0;long ans = 0;while (fast < n) {while (fast < n && data[fast] - data[slow] < c) {fast++;}while (fast < n && data[fast] - data[slow] > c) {slow++;}if (fast < n && data[fast] - data[slow] == c) {int oldFast = fast, oldSlow = slow;while (fast < n && data[fast] == data[oldFast]) {fast++;}while (slow < n && data[slow] == data[oldSlow]) {slow++;}ans += (long) (fast - oldFast) * (slow - oldSlow);}}System.out.println(ans);}
}相关文章:

蓝桥杯第1374题——锻造兵器
题目描述 小明一共有n块锻造石,第块锻造石的属性值为ai. 现在小明决定从这n块锻造石中任取两块来锻造兵器 通过周密计算,小明得出,只有当两块锻造石的属性值的差值等于C,兵器才能锻造成功 请你帮小明算算,他有多少种选…...
坚鹏:政府数字化转型数字机关、数据共享及电子政务类案例研究
政府数字化转型数字机关、数据共享及电子政务类案例研究 课程背景: 很多地方政府存在以下问题: 不清楚政府数字化转型的数字机关类成功案例 不清楚政府数字化转型的数据共享类成功案例 不清楚政府数字化转型的电子政务类成功案例 课程特色&…...
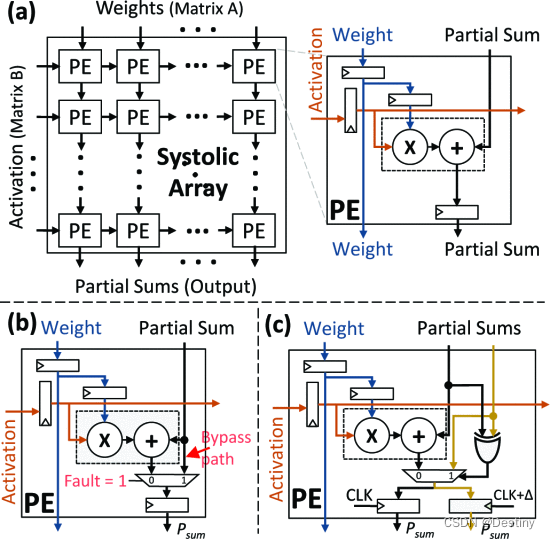
【架构】面向人工智能 (AI) 的硬件的可靠性(2021)
由于激进的技术扩展,现代系统越来越容易受到可靠性威胁的影响,例如软错误、老化和工艺变化。这些威胁在硬件级别表现为位翻转,并且根据位置,可能会损坏输出,从而导致不准确或潜在的灾难性结果。 传统的缓解技术基于冗…...

Unity3D MVC开发模式与开发流程详解
前言 MVC(Model-View-Controller)是一种常用的软件架构模式。将MVC应用于Unity3D开发可以提高项目的可维护性和可扩展性,使代码更加清晰和易于理解。本文将详细介绍Unity3D中MVC开发模式的应用以及开发流程,并给出技术详解和代码…...

简单介绍一下Android里面的IntentFirewall
源码链接 https://android.googlesource.com/platform/frameworks/base//633dc9b/services/java/com/android/server/firewall/IntentFirewall.java 源码如下: package com.android.server.firewall; import android.content.Intent; import android.content.Inte…...

Stable Diffusion 3 发布及其重大改进
1. 引言 就在 OpenAI 发布可以生成令人瞠目的视频的 Sora 和谷歌披露支持多达 150 万个Token上下文的 Gemini 1.5 的几天后,Stability AI 最近展示了 Stable Diffusion 3 的预览版。 闲话少说,我们快来看看吧! 2. 什么是Stable Diffusion…...

【后端】springboot项目
文章目录 1. 2.3.7.RELEASE版本搭建1.1 pom文件1.1.1 方式一1.1.2 方式二 1.2 启动类1.3 测试类 2. 引入Value乱码问题解决 【后端目录贴】 1. 2.3.7.RELEASE版本搭建 1.1 pom文件 1.1.1 方式一 <parent><groupId>org.springframework.boot</groupId><…...

React Native调用摄像头画面及拍照和保存图片到相册全流程
今天主要做了一个demo,功能很简单,就是调用手机摄像头画面,并且可以通过按钮控制拍照以及将图片保存到手机相册的功能,接下来我将从创建项目开始一步一步完成这个demo,各位只需要复制粘贴即可 创建React Native项目 npx react-native init yx_rnDemo --version 0.70.6 // 这里…...

Kubernetes基本部署概念
文章目录 命名空间(Namespaecs)查看命名空间查看带有命名空间对象下资源 文件存储持久卷(pv,Persistent Volumes)卷容量卷模式(volumeMode)访问模式(accessModes)回收策略…...

QT c++ 海康红外热像仪
//本文描述2通道海康通道红外热像仪预览和抓图 #include "mainwindow.h" #include "ui_mainwindow.h" MainWindow::MainWindow(QWidget *parent) : QMainWindow(parent) , ui(new Ui::MainWindow) { ui->setupUi(this); userID-1; …...
OpenAI 的 GPTs 提示词泄露攻击与防护实战:防御卷(一)
前面的OpenAI DevDay活动上,GPTs技术的亮相引起了广泛关注。随着GPTs的创建权限开放给Plus用户,社区里迅速涌现了各种有趣的GPT应用,这些都是利用了Prompt提示词的灵活性。这不仅展示了技术的创新潜力,也让人们开始思考如何获取他…...
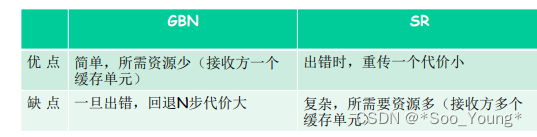
中科大计网学习记录笔记(十五):可靠数据传输的原理
前前言:看过本节的朋友应该都知道本节长度长的吓人,但其实内容含量和之前的差不多,老师在本节课举的例子和解释比较多,所以大家坚持看完是一定可以理解透彻的。本节课大部分是在提出问题和解决问题,先明确出现的问题是…...
五种多目标优化算法(MOGWO、MOJS、NSWOA、MOPSO、MOAHA)性能对比(提供MATLAB代码)
一、5种多目标优化算法简介 1.1MOGWO 1.2MOJS 1.3NSWOA 1.4MOPSO 1.5MOAHA 二、5种多目标优化算法性能对比 为了测试5种算法的性能将其求解9个多目标测试函数(zdt1、zdt2 、zdt3、 zdt4、 zdt6 、Schaffer、 Kursawe 、Viennet2、 Viennet3)࿰…...

力扣:93. 复原 IP 地址
回溯: 1.先定义一个接收的集合,之后再定义一个记录小数点的变量。之后编写回溯函数,终止条件为小数点的个数为3时,同时要判断最后一段的组合的值是否属于ip地址的范围。之后再用for循环来遍历ip地址的组合,先判断组合…...

利用序列化和反序列化实现深拷贝
利用序列化和反序列化可以实现对象的深拷贝,具体步骤如下: 将要深拷贝的对象序列化为字节流。从字节流中反序列化出一个新的对象,即完成了深拷贝。下面是一个示例代码: import java.io.*;class MyClass implements Serializable {private static final long serialVersion…...

【AHK】68键键盘键位布局优化/esc改退格键/回车键
本人习惯使用~作为退格键,但是由于keychron 68键的布局只能用esc平替~来修改,然后也将回车键通过alt和大小写锁定键一起触发 esc::bs ;次步骤与下面步骤相对应,如果是用send bs方式则下面的不生效^esc:: ;通过建立 保留esc功能 send {esc} re…...
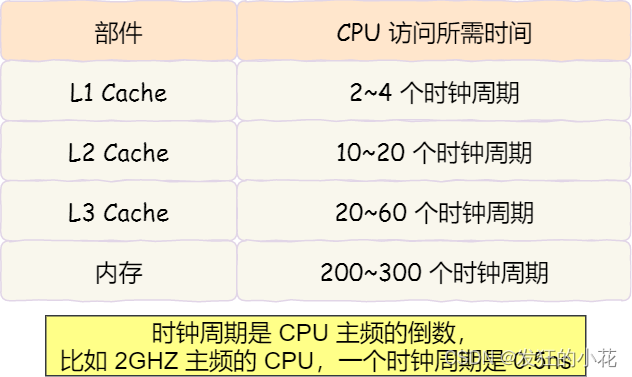
计算机体系架构初步入门
🎬个人简介:一个全栈工程师的升级之路! 📋个人专栏:高性能(HPC)开发基础教程 🎀CSDN主页 发狂的小花 🌄人生秘诀:学习的本质就是极致重复! 目录 1 计算机五大…...

常见的序列化数据结构方法及其优缺点汇总
文章目录 1. JSON (JavaScript Object Notation)2. XML (eXtensible Markup Language)3. YAML (YAML Aint Markup Language)4. Protobuf (Protocol Buffers)5. MessagePack6. BSON (Binary JSON)7. Avro8. Thrift9. CBOR (Concise Binary Object Representation) 将常见的序列化…...
华清远见嵌入式学习——驱动开发——作业1
作业要求: 通过字符设备驱动分步注册过程实现LED驱动的编写,编写应用程序测试,发布到CSDN 作业答案: 运行效果: 驱动代码: #include <linux/init.h> #include <linux/module.h> #include &l…...
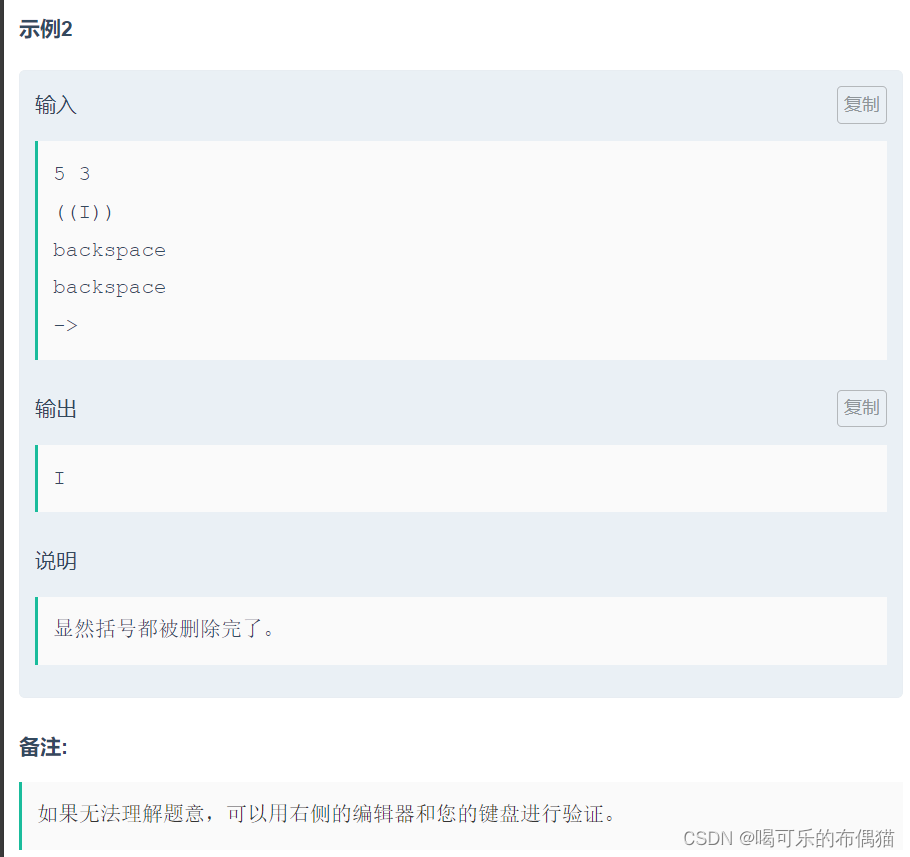
小苯的IDE括号问题(CD) -----牛客小白月赛87(双链表)
C题:C-小苯的IDE括号问题(easy)_牛客小白月赛87 (nowcoder.com) D题: D-小苯的IDE括号问题(hard)_牛客小白月赛87 (nowcoder.com) C题代码: #include<bits/stdc.h>using namespace std…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

Windows 下端口占用排查与释放全攻略
Windows 下端口占用排查与释放全攻略 在开发和运维过程中,经常会遇到端口被占用的问题(如 8080、3306 等常用端口)。本文将详细介绍如何通过命令行和图形化界面快速定位并释放被占用的端口,帮助你高效解决此类问题。 一、准…...

拟合问题处理
在机器学习中,核心任务通常围绕模型训练和性能提升展开,但你提到的 “优化训练数据解决过拟合” 和 “提升泛化性能解决欠拟合” 需要结合更准确的概念进行梳理。以下是对机器学习核心任务的系统复习和修正: 一、机器学习的核心任务框架 机…...
