LeetCode 2476.二叉搜索树最近节点查询:中序遍历 + 二分查找
【LetMeFly】2476.二叉搜索树最近节点查询:中序遍历 + 二分查找
力扣题目链接:https://leetcode.cn/problems/closest-nodes-queries-in-a-binary-search-tree/
给你一个 二叉搜索树 的根节点 root ,和一个由正整数组成、长度为 n 的数组 queries 。
请你找出一个长度为 n 的 二维 答案数组 answer ,其中 answer[i] = [mini, maxi] :
mini是树中小于等于queries[i]的 最大值 。如果不存在这样的值,则使用-1代替。maxi是树中大于等于queries[i]的 最小值 。如果不存在这样的值,则使用-1代替。
返回数组 answer 。
示例 1 :

输入:root = [6,2,13,1,4,9,15,null,null,null,null,null,null,14], queries = [2,5,16] 输出:[[2,2],[4,6],[15,-1]] 解释:按下面的描述找出并返回查询的答案: - 树中小于等于 2 的最大值是 2 ,且大于等于 2 的最小值也是 2 。所以第一个查询的答案是 [2,2] 。 - 树中小于等于 5 的最大值是 4 ,且大于等于 5 的最小值是 6 。所以第二个查询的答案是 [4,6] 。 - 树中小于等于 16 的最大值是 15 ,且大于等于 16 的最小值不存在。所以第三个查询的答案是 [15,-1] 。
示例 2 :
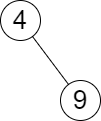
输入:root = [4,null,9], queries = [3] 输出:[[-1,4]] 解释:树中不存在小于等于 3 的最大值,且大于等于 3 的最小值是 4 。所以查询的答案是 [-1,4] 。
提示:
- 树中节点的数目在范围
[2, 105]内 1 <= Node.val <= 106n == queries.length1 <= n <= 1051 <= queries[i] <= 106
方法一:中序遍历 + 二分查找
首先要明确的是:
题目给的二叉搜索树不一定是平衡树。因此最坏的情况下,题目给的二叉搜索树可能会退化成一条链,单词搜索的时间复杂度可能会达到 O ( n ) O(n) O(n)。
因为可能有很多次查询( 1 0 5 10^5 105),所以我们可以预处理二叉搜索树:
我们知道二叉搜索树的中序遍历结果是递增的,因此我们中序遍历一遍二叉搜索树,就得到了二叉树所有节点值的递增数组。
这样,我们只需要遍历每一个查询,二分查找想要的答案即可:
对于查询 q q q,使用内置函数
lower_bound/bisect_left等找到第一个 ≥ q \geq q ≥q的位置 l o c loc loc。判断 l o c loc loc是否超出数组范围:
- 若超出:说明无比 q q q大的数, M M M应为(默认值)
-1- 否则: M = v [ l o c ] M=v[loc] M=v[loc]。此时若 M M M恰好等于 q q q则可直接得到 m = M m=M m=M
m m m仍未默认值
-1的话,还要判断 l o c loc loc是否非零:
- 若非零:则 m = v [ l o c − 1 ] m=v[loc-1] m=v[loc−1]
- 否则: m m m为默认值
-1
- 时间复杂度 O ( N + Q log N ) O(N+Q\log N) O(N+QlogN),其中 N N N是二叉树节点个数, Q Q Q是查询个数
- 空间复杂度 O ( N ) O(N) O(N)
AC代码
C++
class Solution {
private:vector<int> v;void dfs(TreeNode* root) {if (!root) {return;}dfs(root->left);v.push_back(root->val);dfs(root->right);}public:vector<vector<int>> closestNodes(TreeNode* root, vector<int>& queries) {dfs(root);vector<vector<int>> ans(queries.size());for (int i = 0; i < queries.size(); i++) {int m = -1, M = -1;vector<int>::iterator it = lower_bound(v.begin(), v.end(), queries[i]);if (it != v.end()) {M = *it;if (M == queries[i]) {m = M;goto loop;}}if (it != v.begin()) {m = *(it - 1);}loop:ans[i] = {m, M};}return ans;}
};
Python
# from typing import List, Optional
# from bisect import bisect_left# # Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = rightclass Solution:def dfs(self, root: Optional[TreeNode]) -> None:if not root:returnself.dfs(root.left)self.v.append(root.val)self.dfs(root.right)def closestNodes(self, root: TreeNode, queries: List[int]) -> List[List[int]]:self.v = []self.dfs(root)ans = []for q in queries:m, M = -1, -1loc = bisect_left(self.v, q)if loc != len(self.v):M = self.v[loc] # v1中这里笔误写成M=loc了if M == q:ans.append([q, q])continueif loc:m = self.v[loc - 1]ans.append([m, M])return ans
同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/136269516
相关文章:

LeetCode 2476.二叉搜索树最近节点查询:中序遍历 + 二分查找
【LetMeFly】2476.二叉搜索树最近节点查询:中序遍历 二分查找 力扣题目链接:https://leetcode.cn/problems/closest-nodes-queries-in-a-binary-search-tree/ 给你一个 二叉搜索树 的根节点 root ,和一个由正整数组成、长度为 n 的数组 qu…...

选座位 - 华为OD统一考试(C卷)
OD统一考试(C卷) 分值: 200分 题解: Java / Python / C 题目描述 疫情期间,需要大家保证一定的社交距离,公司组织开交流会议,座位有一排共N个座位,编号分别为[0…N-1],要…...
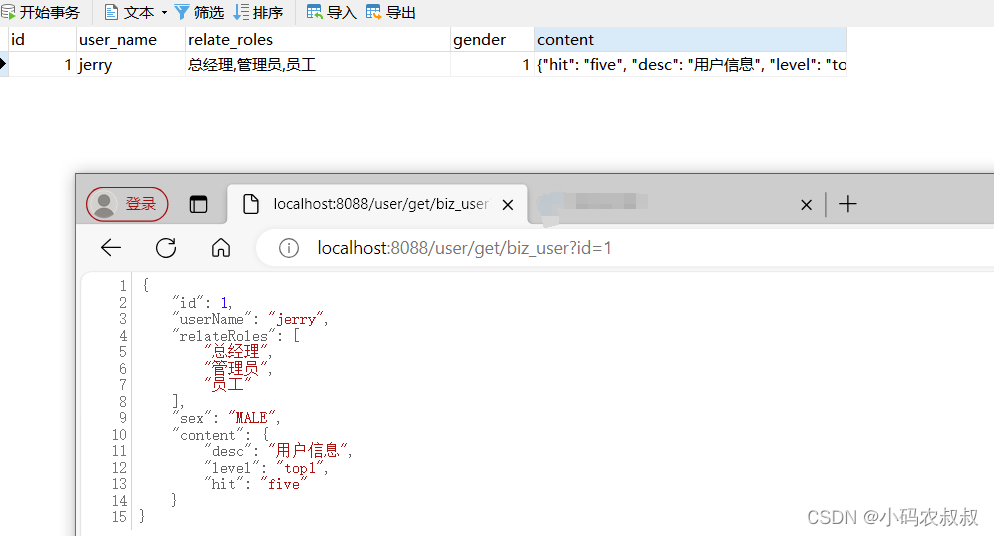
【微服务】mybatis typehandler使用详解
目录 一、前言 二、TypeHandler简介 2.1 什么是TypeHandler 2.1.1 TypeHandler特点 2.2 TypeHandler原理 2.3 mybatis自带的TypeHandler 三、环境准备 3.1 准备一张数据表 3.2 搭建一个springboot工程 3.2.1 基础依赖如下 3.2.2 核心配置文件 3.2.3 测试接口 四、T…...

计网 - 深入理解HTTPS:加密技术的背后
文章目录 Pre发展历史Http VS HttpsHTTPS 解决了 HTTP 的哪些问题HTTPS是如何解决上述三个风险的混合加密摘要算法 数字签名数字证书 Pre PKI - 数字签名与数字证书 PKI - 借助Nginx 实现Https 服务端单向认证、服务端客户端双向认证 发展历史 HTTP(超文本传输协…...

Jmeter之单接口的性能测试
前言: 服务端的整体性能测试是一个非常复杂的概念,包含生成虚拟用户,模拟并发,分析性能结果等各种技术,期间可能还要解决设计场景、缓存影响、第三方接口mock、IP限制等问题。如何用有限的测试机器,在测试环…...

成像光谱遥感技术中的AI革命:ChatGPT应用指南
“成像光谱遥感技术中的人工智能革命:ChatGPT应用指南”,这是一门旨在改变您使用人工智能处理遥感数据的方式。将最新的人工智能技术与实际的遥感应用相结合,提供不仅是理论上的,而且是适用和可靠的工具和方法。无论你是经验丰富的…...

掌握BeautifulSoup4:爬虫解析器的基础与实战【第91篇—BeautifulSoup4】
掌握BeautifulSoup4:爬虫解析器的基础与实战 网络上的信息浩如烟海,而爬虫技术正是帮助我们从中获取有用信息的重要工具。在爬虫过程中,解析HTML页面是一个关键步骤,而BeautifulSoup4正是一款功能强大的解析器,能够轻…...

从源码解析Kruise(K8S)原地升级原理
从源码解析Kruise原地升级原理 本文从源码的角度分析 Kruise 原地升级相关功能的实现。 本篇Kruise版本为v1.5.2。 Kruise项目地址: https://github.com/openkruise/kruise 更多云原生、K8S相关文章请点击【专栏】查看! 原地升级的概念 当我们使用deployment等Wor…...

2024年【广东省安全员C证第四批(专职安全生产管理人员)】复审考试及广东省安全员C证第四批(专职安全生产管理人员)模拟考试题
题库来源:安全生产模拟考试一点通公众号小程序 广东省安全员C证第四批(专职安全生产管理人员)复审考试是安全生产模拟考试一点通总题库中生成的一套广东省安全员C证第四批(专职安全生产管理人员)模拟考试题࿰…...
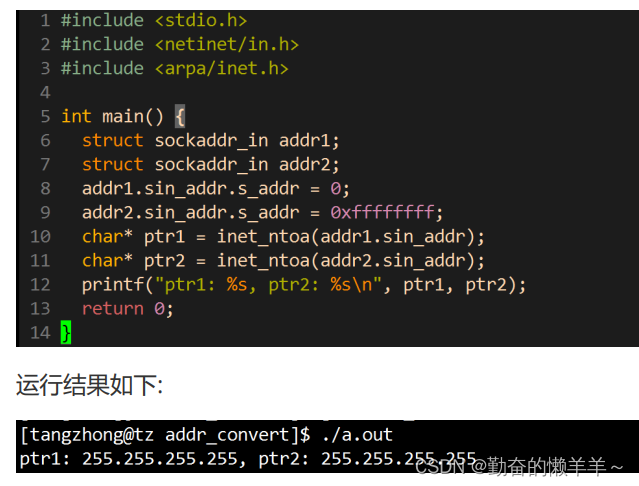
udp服务器【Linux网络编程】
目录 一、UDP服务器 1、创建套接字 2、绑定套接字 3、运行 1)读取数据 2)发送数据 二、UDP客户端 创建套接字: 客户端不用手动bind 收发数据 处理消息和网络通信解耦 三、应用场景 1、服务端执行命令 2、Windows上的客户端 3…...
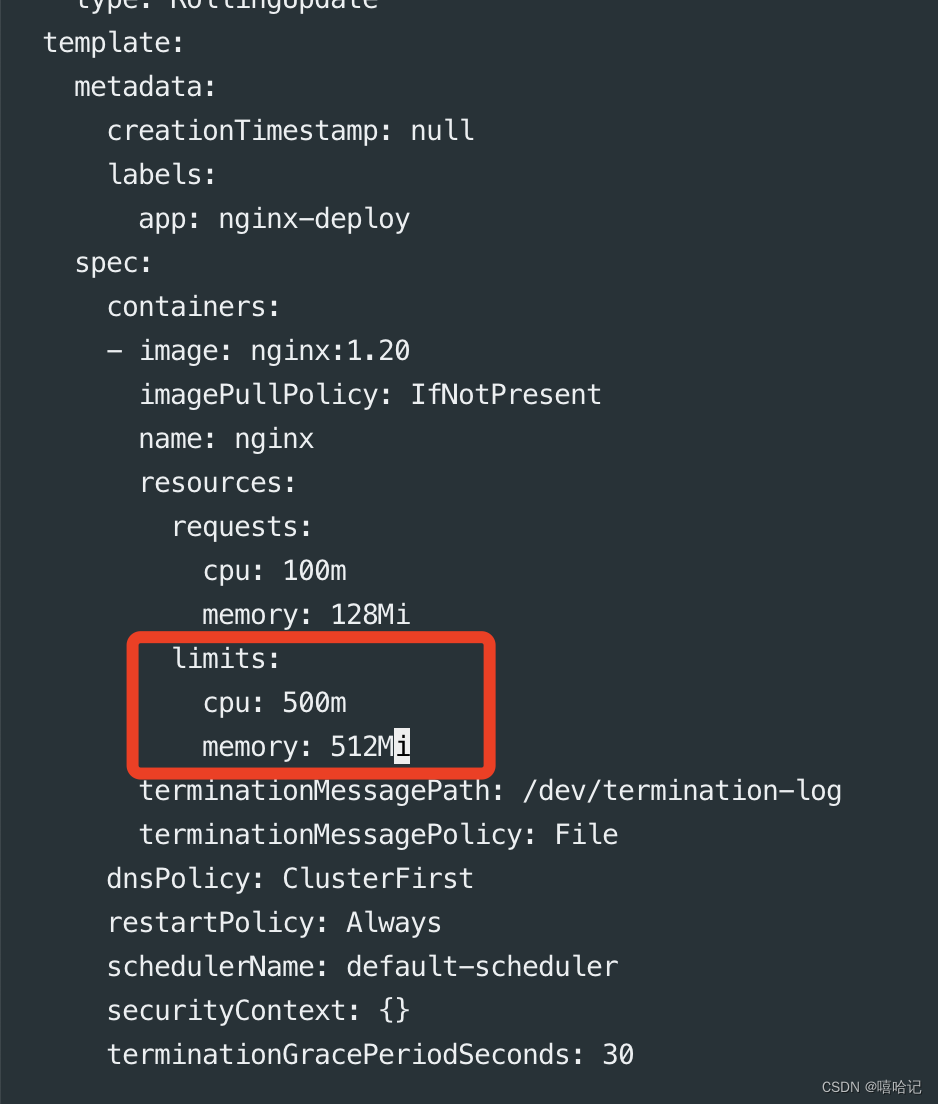
【k8s资源调度-Deployment】
1、标签和选择器 1.1 标签Label 配置文件:在各类资源的sepc.metadata.label 中进行配置通过kubectl 命令行创建修改标签,语法如下 创建临时label:kubectl label po <资源名称> apphello -n <命令空间(可不加࿰…...
【Oracle】玩转Oracle数据库(五):PL/SQL编程
前言 嗨,各位数据库达人!准备好迎接数据库编程的新挑战了吗?今天我们要探索的是Oracle数据库中的神秘魔法——PL/SQL编程!🔮💻 在这篇博文【Oracle】玩转Oracle数据库(五)࿱…...
JavaScript流程控制
文章目录 1. 顺序结构2. 分支结构2.1 if 语句2.2 if else 双分支语句2.3 if else if 多分支语句三元表达式 2.4 switch 语句switch 语句和 if else if语句区别 3. 循环结构3.1 for 循环断点调试 3.2 双重 for 循环3.3 while 循环3.4 do while 循环3.5 contiue break 关键字 4. …...

五个使用Delphi语言进行开发的案例
案例一:学生信息管理系统 某学校需要开发一个学生信息管理系统,用于记录学生的基本信息、成绩和考勤情况等。开发者使用Delphi语言进行开发,设计了一个包含多个窗体的应用程序。主窗体用于展示学生的列表和基本信息,其他窗体则用…...

蓝桥杯第1374题——锻造兵器
题目描述 小明一共有n块锻造石,第块锻造石的属性值为ai. 现在小明决定从这n块锻造石中任取两块来锻造兵器 通过周密计算,小明得出,只有当两块锻造石的属性值的差值等于C,兵器才能锻造成功 请你帮小明算算,他有多少种选…...
坚鹏:政府数字化转型数字机关、数据共享及电子政务类案例研究
政府数字化转型数字机关、数据共享及电子政务类案例研究 课程背景: 很多地方政府存在以下问题: 不清楚政府数字化转型的数字机关类成功案例 不清楚政府数字化转型的数据共享类成功案例 不清楚政府数字化转型的电子政务类成功案例 课程特色&…...
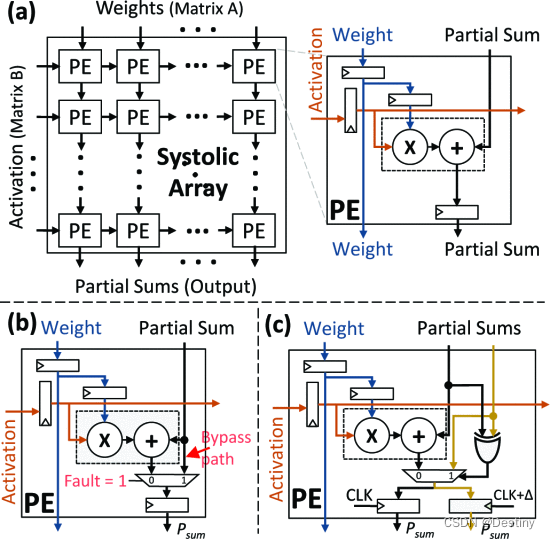
【架构】面向人工智能 (AI) 的硬件的可靠性(2021)
由于激进的技术扩展,现代系统越来越容易受到可靠性威胁的影响,例如软错误、老化和工艺变化。这些威胁在硬件级别表现为位翻转,并且根据位置,可能会损坏输出,从而导致不准确或潜在的灾难性结果。 传统的缓解技术基于冗…...

Unity3D MVC开发模式与开发流程详解
前言 MVC(Model-View-Controller)是一种常用的软件架构模式。将MVC应用于Unity3D开发可以提高项目的可维护性和可扩展性,使代码更加清晰和易于理解。本文将详细介绍Unity3D中MVC开发模式的应用以及开发流程,并给出技术详解和代码…...

简单介绍一下Android里面的IntentFirewall
源码链接 https://android.googlesource.com/platform/frameworks/base//633dc9b/services/java/com/android/server/firewall/IntentFirewall.java 源码如下: package com.android.server.firewall; import android.content.Intent; import android.content.Inte…...

Stable Diffusion 3 发布及其重大改进
1. 引言 就在 OpenAI 发布可以生成令人瞠目的视频的 Sora 和谷歌披露支持多达 150 万个Token上下文的 Gemini 1.5 的几天后,Stability AI 最近展示了 Stable Diffusion 3 的预览版。 闲话少说,我们快来看看吧! 2. 什么是Stable Diffusion…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...
