LeetCode49 字母异位词分组
LeetCode49 字母异位词分组
在这篇博客中,我们将探讨 LeetCode 上的一道经典算法问题:字母异位词分组。这个问题要求将给定的字符串数组中的字母异位词组合在一起,并以任意顺序返回结果列表。
问题描述
给定一个字符串数组 strs,要求将其中的字母异位词组合在一起,并返回组合后的结果列表。字母异位词是由重新排列源单词的所有字母得到的新单词。
解决方案思路
我们可以使用哈希表来解决这个问题。具体的思路如下:
- 创建一个哈希表
unordered_map<string, vector<string>>,用于存储排序后的字符串和对应的原始字符串数组。 - 遍历输入的字符串数组
strs,对于每个字符串str:- 将其排序后得到的字符串
sorted_str作为键,原始字符串str添加到哈希表中相应键对应的向量中。
- 将其排序后得到的字符串
- 遍历哈希表,将每个键对应的值(即原始字符串数组)放入结果列表中。
下面是用 C++ 实现的解决方案:
class Solution {
public:vector<vector<string>> groupAnagrams(vector<string>& strs) {// 创建哈希表unordered_map<string, vector<string>> M;// 遍历字符串数组for (string str : strs) {// 将字符串排序string sorted_str = str;sort(sorted_str.begin(), sorted_str.end());// 将排序后的字符串作为键,将原始字符串添加到对应的向量中M[sorted_str].push_back(str);}// 将哈希表中的结果转换为答案列表vector<vector<string>> ans;for (auto pair : M) {ans.push_back(pair.second);}return ans;}
};
复杂度分析
时间复杂度
- 排序字符串: 对于给定的每个字符串,需要将其排序,时间复杂度为 O ( k log k ) O(k \log k) O(klogk),其中 k k k 是字符串的最大长度。
- 遍历字符串数组: 遍历整个字符串数组并将其添加到哈希表中,时间复杂度为 O ( n ) O(n) O(n),其中 n n n 是字符串数组的大小。
- 构建结果列表: 遍历哈希表并构建结果列表,时间复杂度为 O ( m ) O(m) O(m),其中 m m m 是哈希表中键值对的数量。
综上所述,总体时间复杂度为 O ( n ⋅ k log k + m ) O(n \cdot k \log k + m) O(n⋅klogk+m)。
空间复杂度
- 哈希表存储: 使用了哈希表存储每个排好序的字符串及其对应的源字符串数组,空间复杂度为 O ( n ) O(n) O(n),其中 n n n 是字符串数组的大小。
因此,该算法的空间复杂度为 O ( n ) O(n) O(n)。
通过以上分析,我们可以看到,这种基于哈希表的解决方案在时间和空间复杂度上都具有较好的性能,能够高效地解决字母异位词分组的问题。
总结
字母异位词分组问题可以通过使用哈希表来有效地解决。通过对每个字符串进行排序,并将排序后的字符串作为键,我们可以将具有相同字母组成的单词分组在一起。最终,我们将哈希表中的结果转换为答案列表,即得到了按要求分组的字母异位词列表。
相关文章:

LeetCode49 字母异位词分组
LeetCode49 字母异位词分组 在这篇博客中,我们将探讨 LeetCode 上的一道经典算法问题:字母异位词分组。这个问题要求将给定的字符串数组中的字母异位词组合在一起,并以任意顺序返回结果列表。 问题描述 给定一个字符串数组 strs࿰…...
【Python】Windows本地映射远程Linux服务器上的端口(解决jupyter notebook无法启动问题)
创作日志: 学习深度学习不想在本地破电脑上再安装各种软件,我就用实验室的服务器配置环境,启动jupyter notebook时脑子又瓦特了,在自己Windows电脑上打开服务器提供的网址,那肯定打不开啊,以前在其它电脑上…...

C++面试:用户态和内核态的基本概念、区别
目录 一、基本概念 概念: 区别: 二、Windows示例 基础介绍 用户态到内核态的切换过程: 程序实例 三、Linux示例 特权级别: 用户态到内核态的切换过程: 调度和中断处理: 程序实例 总结 在操作系…...
)
Vue计算属性computed()
1. 计算属性定义 获取计算属性值 <div>{{ 计算属性名称}}</div>创建计算属性 let 定义的属性ref/reactive....let 计算属性名称 computed(() > {//这里写函数式,函数式里面包含定义属性//只有这个包含的定义属性被修改时才出发此函数式//通过计算属性名称co…...
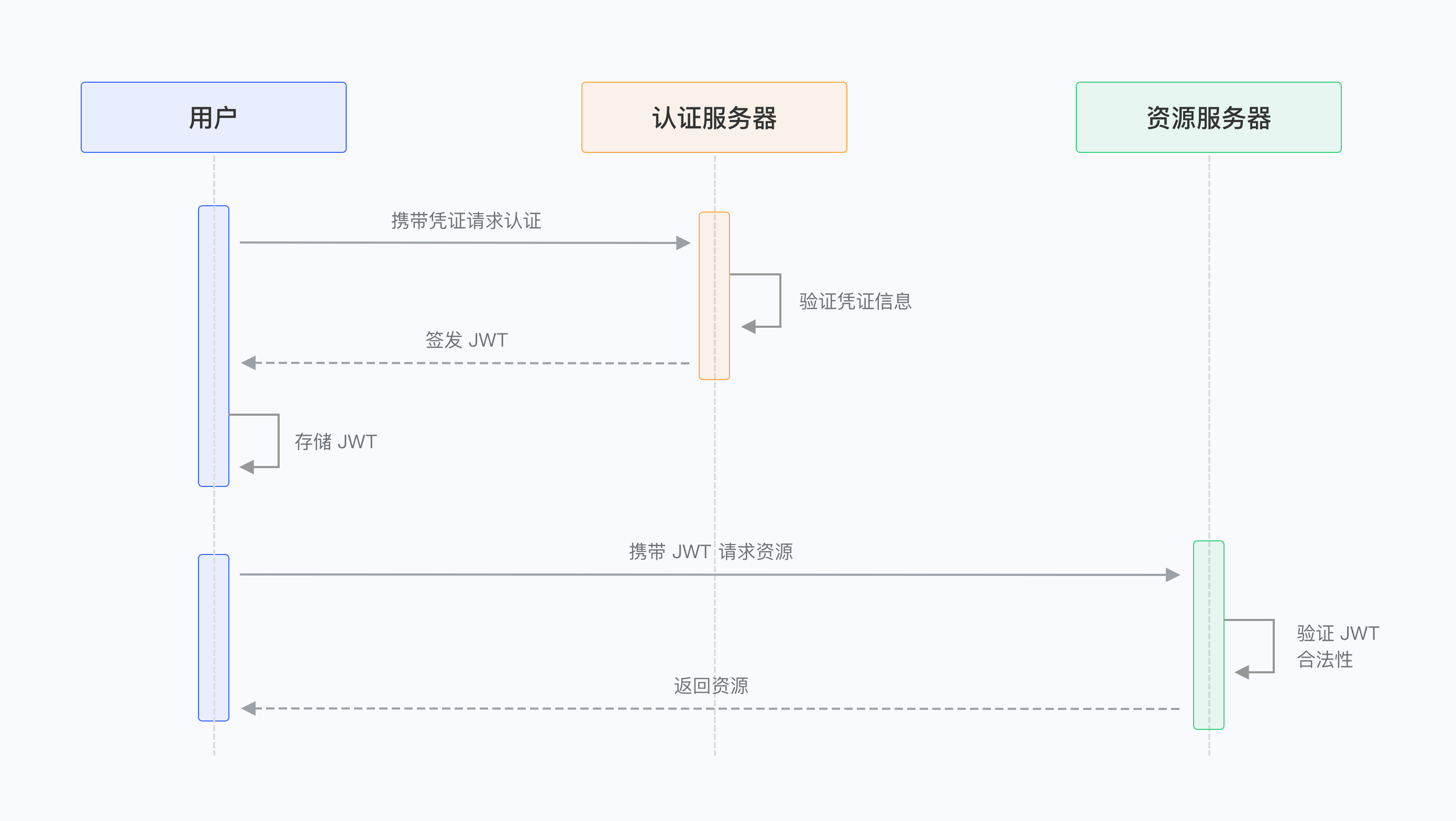
JWT学习笔记
了解 JWT Token 释义及使用 | Authing 文档 JSON Web Token Introduction - jwt.io JSON Web Token (JWT,RFC 7519 (opens new window)),是为了在网络应用环境间传递声明而执行的一种基于 JSON 的开放标准((RFC 7519)。该 token 被设计为紧凑…...
WSL里的Ubuntu 登录密码忘了怎么更改
环境: Win10 专业版 WSL2 如何 Ubuntu22.04 问题描述: WSL里的Ubuntu 登录密码忘了怎么更改 解决方案: 在WSL中的Ubuntu系统中,忘记了密码,可以通过以下步骤重置密码: 1.打开命令提示符或PowerShel…...
【软件测试面试】要你介绍项目-如何说?完美面试攻略...
目录:导读 前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜) 前言 1、测试面试时&am…...

【Crypto | CTF】RSA打法 集合
天命:我发现题题不一样,已知跟求知的需求都不一样 题目一:已知 p q E ,计算T,最后求D 已知两个质数p q 和 公钥E ,通过p和q计算出欧拉函数T,最后求私钥D 【密码学 | CTF】BUUCTF RSA-CSDN…...

在springboot中调用openai Api并实现流式响应
之前在《在springboot项目中调用openai API及我遇到的问题》这篇博客中,我实现了在springboot中调用openai接口,但是在这里的返回的信息是一次性全部返回的,如果返回的文字比较多,我们可能需要等很久。 所以需要考虑将请求接口响应…...

C++构造函数重难点解析
一、C构造函数是什么 C的构造函数是一种特殊的成员函数,用于初始化类的对象。它具有与类相同的名称,并且没有返回类型。构造函数在创建对象时自动调用,并且可以执行必要的初始化操作。 二、C构造函数特点 类的构造函数不能被继承,…...
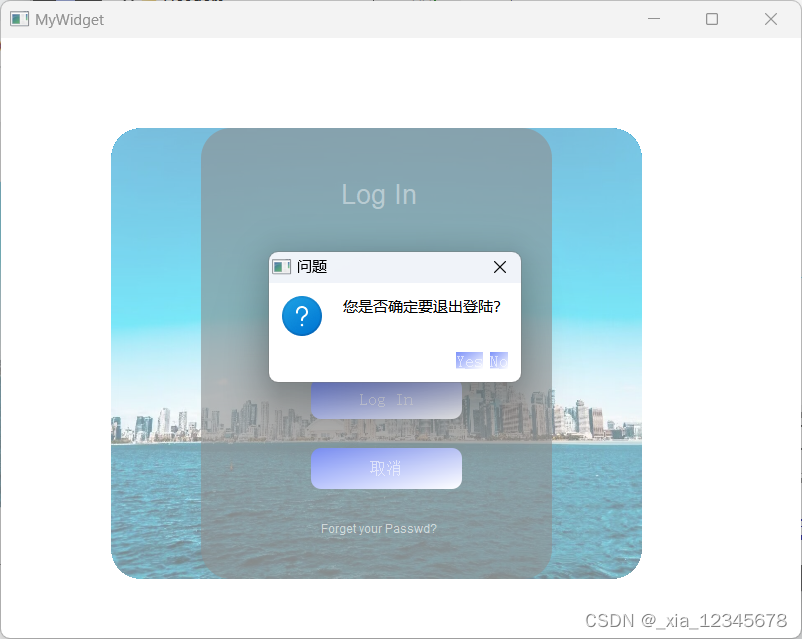
QT day3 作业2.22
思维导图: 作业: 完善对话框,点击登录对话框,如果账号和密码匹配,则弹出信息对话框,给出提示”登录成功“,提供一个Ok按钮,用户点击Ok后,关闭登录界面,跳转到…...
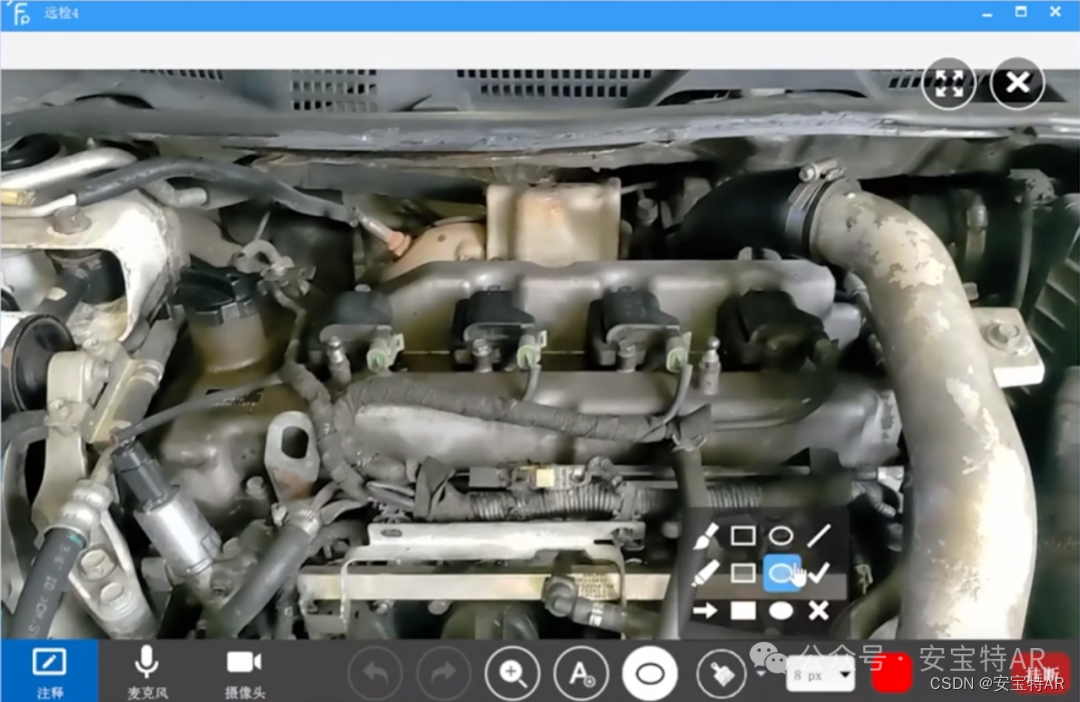
AR汽车行业解决方案系列之2-远程汽修
在汽车行业中,AR技术的应用正悄然改变着整个产业链的运作方式,应用涵盖培训、汽修、汽车售后、PDI交付、质检以及汽车装配等,AR技术为多个环节都带来了前所未有的便利与效率提升。 安宝特AR将以系列推文的形式为读者逐一介绍在汽车行业中安宝…...

每日五道java面试题之spring篇(五)
目录: 第一题. 使用 Spring 有哪些方式?第二题. 什么是Spring IOC 容器?第三题. 控制反转(IoC)有什么作用?第四题. IOC的优点是什么?第五题. BeanFactory 和 ApplicationContext有什么区别? 第一题. 使用 Spring 有哪…...
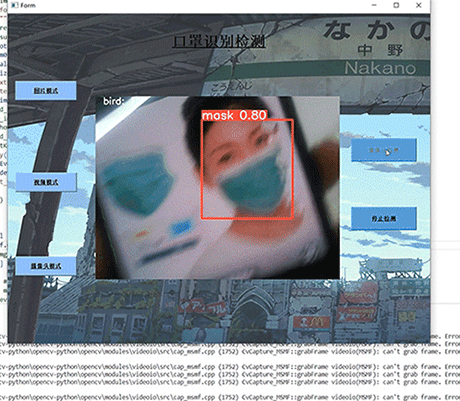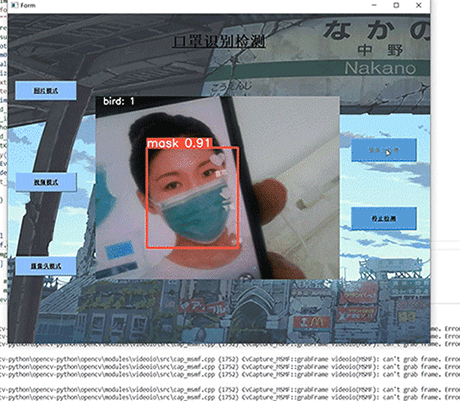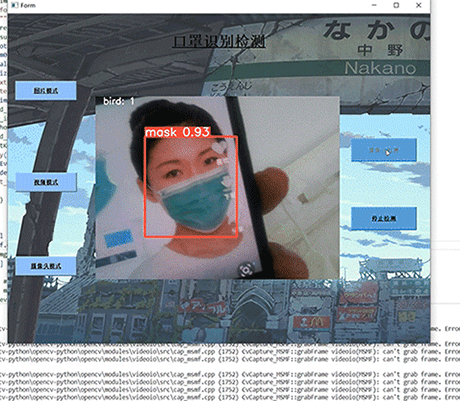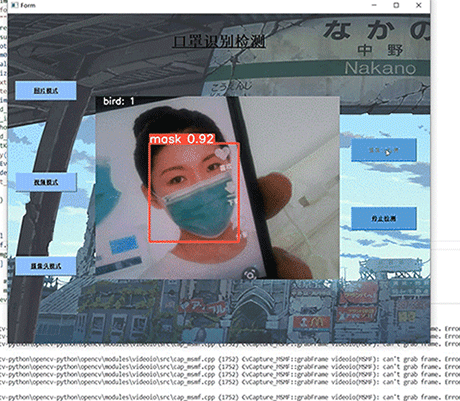
挑战杯 基于YOLO实现的口罩佩戴检测 - python opemcv 深度学习
文章目录 0 前言1 课题介绍2 算法原理2.1 算法简介2.2 网络架构 3 关键代码4 数据集4.1 安装4.2 打开4.3 选择yolo标注格式4.4 打标签4.5 保存 5 训练6 实现效果6.1 pyqt实现简单GUI6.3 视频识别效果6.4 摄像头实时识别 7 最后 0 前言 🔥 优质竞赛项目系列…...
12. Springboot集成Dubbo3(三)Dubbo-Admin
目录 1、前言 2、安装 2.1、下载Dubbo-admin 2.2、修改配置 2.3、编译前端 2.4、访问 2.5、加载自己的服务 2.6、服务测试 2.7、其他 3、小结 1、前言 Dubbo Admin是用于管理Dubbo服务的基于Web的管理工具。Dubbo Admin提供了一个用户友好的界面,用于在分…...
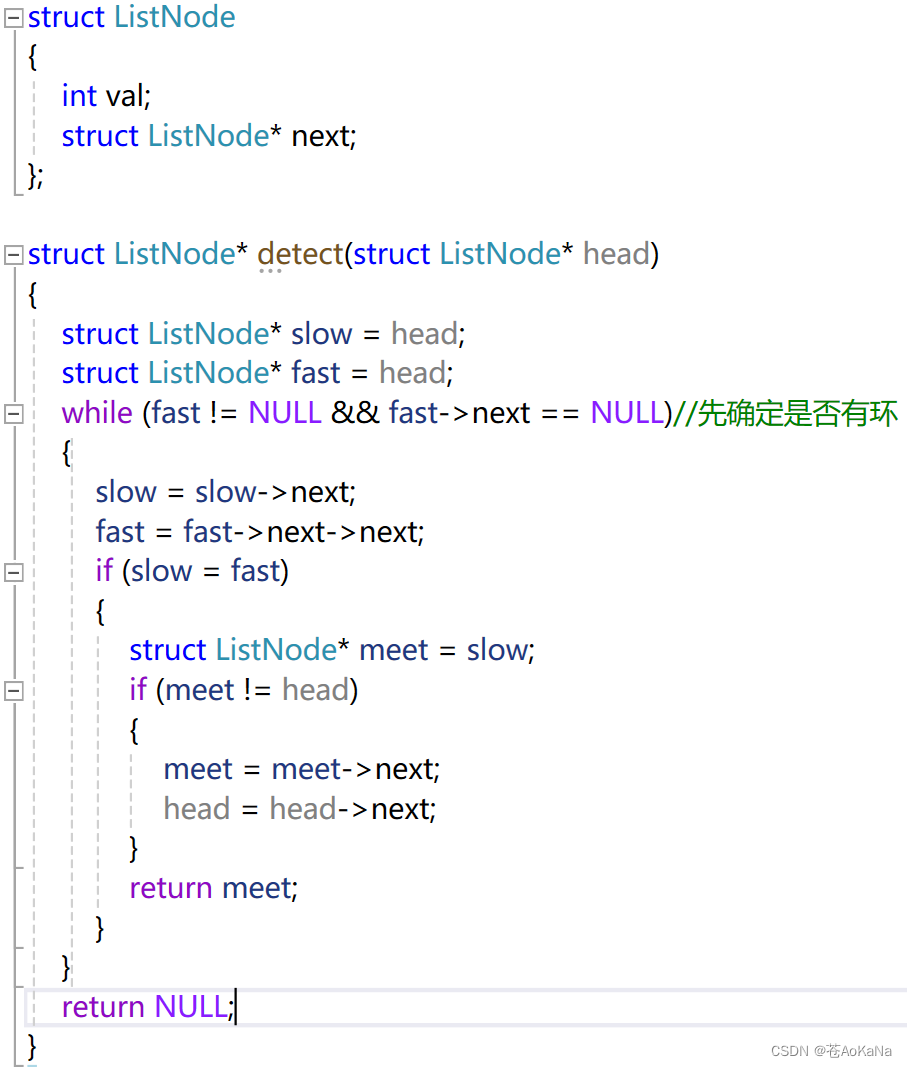
c语言的数据结构:找环状链表入口处
一起<( ̄︶ ̄)↗[GO!] 1.如何判断一个链表是否有环 思路:设定两个快慢指针fast和slow,fast每次走两个结点,slow每次走一个节点 如果fast指针遇到了Null,那么这个链表没有环,如果fast和slow可以相遇,则代表这个链表有环 代码如下 N:fast先进环,slow后…...

LabVIEW声速测定实验数据处理
LabVIEW声速测定实验数据处理 介绍了一个基于LabVIEW的声速测定实验数据处理系统的应用。该系统利用LabVIEW的强大数据处理和分析能力,通过设计友好的用户界面和高效的算法,有效提高了声速测定实验的数据处理效率和准确性。通过这个案例,可以…...

深入剖析C语言中的段错误:从内存模型到实战调试全方位解析
引言 在C语言编程的世界里,段错误(Segmentation Fault)无疑是最常见的运行时错误之一。它源自程序对内存的非法访问,可能由于数组越界、野指针、悬垂指针、栈溢出等各种原因造成。本篇文章旨在带领读者深入探索C语言中的内存管理…...

1.操作Python入门Python安装和使用教程
1. 命令行与环境 为获取各种设置信息,CPython 解析器会扫描命令行与环境。 CPython 实现细节: 其他实现的命令行方案可能会有所不同。 详见 其他实现。 1.1. 命令行 调用 Python 时,可以指定下列任意选项: python [-bBdEhiIO…...
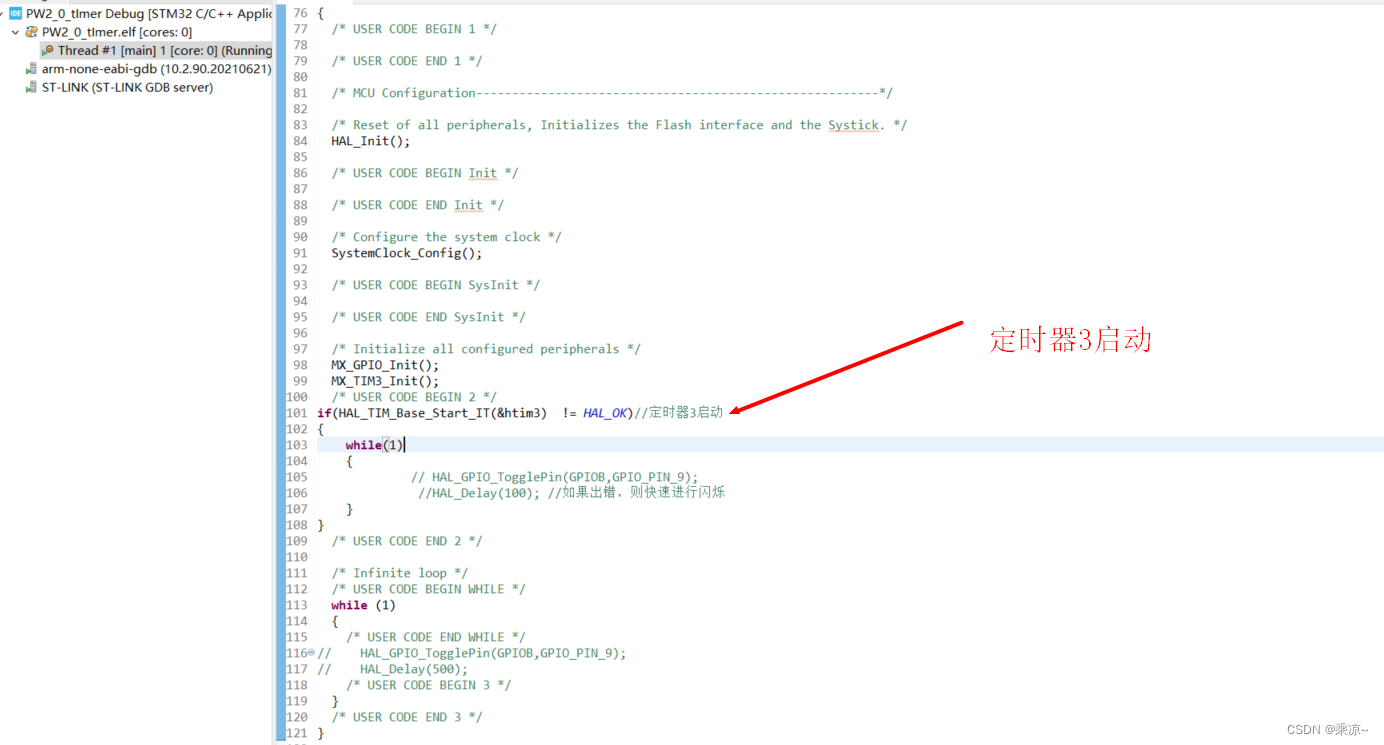
STM32G030C8T6:定时器1ms中断(以64MHz外部晶振为例)
本专栏记录STM32开发各个功能的详细过程,方便自己后续查看,当然也供正在入门STM32单片机的兄弟们参考; 本小节的目标是,系统主频64 MHZ,采用高速外部晶振,通过定时器3 每秒中断控制 PB9 引脚输出高低电平,从…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

如何配置一个sql server使得其它用户可以通过excel odbc获取数据
要让其他用户通过 Excel 使用 ODBC 连接到 SQL Server 获取数据,你需要完成以下配置步骤: ✅ 一、在 SQL Server 端配置(服务器设置) 1. 启用 TCP/IP 协议 打开 “SQL Server 配置管理器”。导航到:SQL Server 网络配…...
