【C++】AVL树,平衡二叉树详细解析
文章目录
- 前言
- 1.AVL树的概念
- 2.AVL树节点的定义
- 3.AVL树的插入
- 4.AVL树的旋转
- 左单旋
- 右单旋
- 左右双旋
- 右左双旋
- AVL树的验证
- AVL树的删除
- AVL树的性能
前言
前面对map/multimap/set/multiset进行了简单的介绍,在其文档介绍中发现,这几个容器有个共同点是:其底层都是按照二叉搜索树来实现的,但是二叉搜索树有其自身的缺陷,假如往树中插入的元素有序或者接近有序,二叉搜索树就会退化成单支树,时间复杂度会退化成O(N),因此map、set等关联式容器的底层结构是对二叉树进行了平衡处理,即采用平衡二叉树树来实现。
1.AVL树的概念
AVL树,又称平衡二叉搜索树。二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),左右子树的高度差被称为平衡因子(平衡因子=右子树高度-左子树高度),即可降低树的高度,从而减少平均搜索长度。
AVL树可以是一棵空树,也可能是具有一下性质的一棵平衡二叉树:
- 树的左右子树都是一棵AVL树
- 树的左右子树高度之差(平衡因子)的绝对值不超过1(可以是-1,0,1)
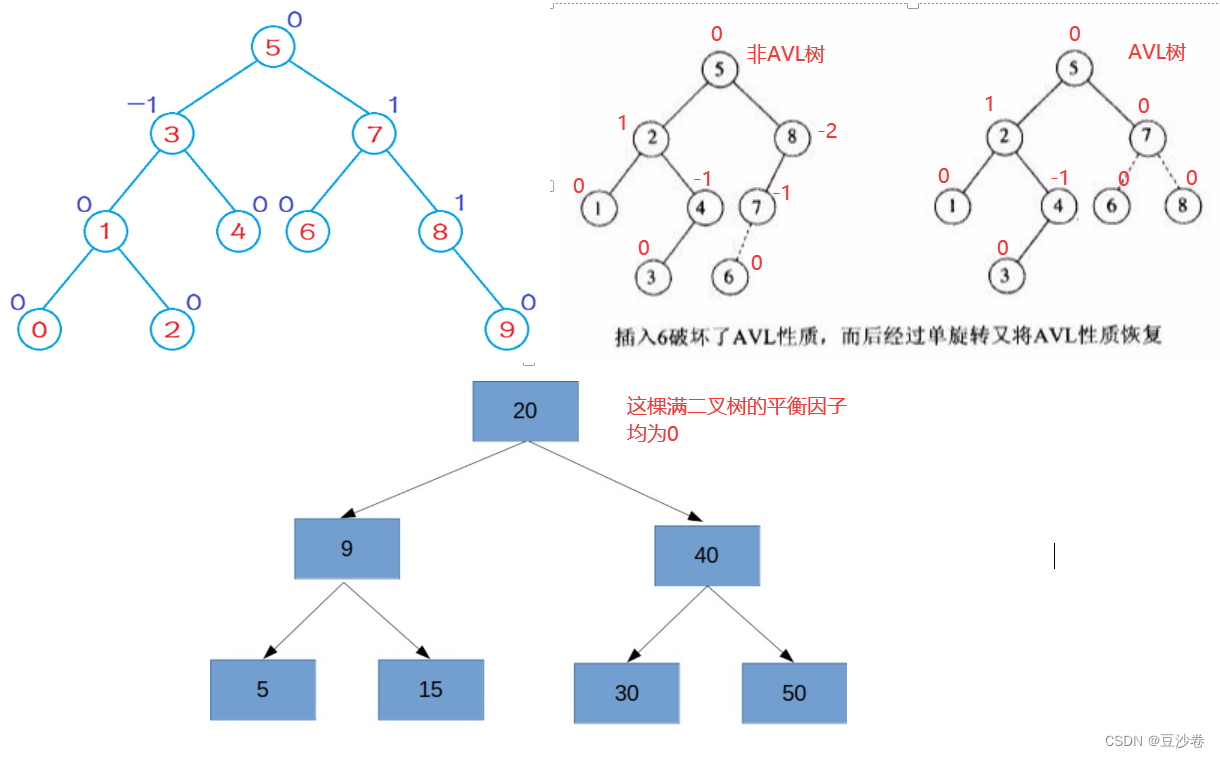
如果一棵二叉树是高度平衡的,它就是AVL树,如果它有n个结点,其高度可保持在O(logN),搜索时间复杂度为O(NlogN)。
2.AVL树节点的定义
我们需要实现一个KV模型的AVL树,在这里最好定义成三叉链的结构,多引入一个_parent(父节点),方便后序插入等操作。除此之外还要在每个结点中引入平衡因子,由于新构造的结点的左右子树均为空树,所以初始化的时候将平衡因子设置为0就好。
为什么要设置平衡因子?为什么要设置成三叉链结构?
由于我们插入结点后需要倒着往上进行平衡因子的更新,所以我们将AVL树结点的结构设置为了三叉链结构,这样我们就可以通过父指针找到其父结点,进而对其平衡因子进行更新。当然,我们也可以不用三叉链结构,可以在插入结点时将路径上的结点存储到一个栈当中,当我们更新平衡因子时也可以通过这个栈来更新祖先结点的平衡因子,但是相对较麻烦。
注意平衡因子不是必须的,它只是AVL树其中一种实现方式,采用其它方法也可以判断左右子树高度差绝对值是否小于等于1,但是我认为引入平衡因子可以给我们更加直观的呈现平衡二叉树的整体特征。
//定义AVL树的结点
//三叉链+平衡因子
template<class K,class V>
struct AVLTreeNode
{//存储<key,value>数据的结点pairpair<K,V> _kv;//三叉链AVLTreeNode<K, V>* _parent;AVLTreeNode<K, V>* _left;AVLTreeNode<K, V>* _right;int _bf;//平衡因子=右子树高度-左子树高度(-1,0,1)//结点的构造函数AVLTreeNode(const pair<K,V>& kv):_kv(kv), _parent(nullptr), _left(nullptr), _right(nullptr),_bf(0){}
};
3.AVL树的插入
思路:
- 插入数据到平衡二叉树中,我们首先需要一个根
- 按照二叉搜索树的插入方法,找到待插入位置。
待插入结点的key值比当前结点小就插入到该结点的左子树。
待插入结点的key值比当前结点大就插入到该结点的右子树。
待插入结点的key值与当前结点的key值相等就插入失败。 - 找到待插入位置后,将待插入结点插入到树中。(注意保持三叉链结构)
- 更新平衡因子: 一个结点的平衡因子是否需要更新,是取决于该结点的左右子树的高度是否发生了变化,因此插入一个结点后,该结点的祖先结点的平衡因子可能也需要更新。
新增结点在parent的右边,parent的平衡因子+ + 。
新增结点在parent的左边,parent的平衡因子− − 。
每更新完一个结点的平衡因子后,还需要再进行以下判断:
如果parent的平衡因子等于-1或者1,表明还需要继续往上更新平衡因子。
如果parent的平衡因子等于0,表明无需继续往上更新平衡因子了。
如果parent的平衡因子等于-2或者2,表明此时以parent结点为根结点的子树已经不平衡了,需要进行旋转处理。
注意: parent的平衡因子在更新前只可能是-1/0/1(AVL树中每个结点的左右子树高度之差的绝对值不超过1)。
跳出循环的条件
在最坏情况下,平衡因子时一路更新到根结点。直到找到与待插入结点的key值相同的结点判定为插入失败,或者最终走到空树位置进行结点插入。所以循环的条件是parent不为空,这也是使用三叉链结构的原因,我们可以迭代着往上走。
插入代码如下:
template<class K,class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public://插入函数:我们需要将给的pair数据插入到AVL树中。bool insert(const pair<K, V>& kv){//1.插入数据到平衡二叉树中,我们首先需要一个根if (_root == nullptr){_root = new Node(kv);return true;}//2.根据二叉搜索树的特性(小的往左走,大的往右走),找到适合插入的位置Node* parent = nullptr;Node* cur = _root;//从根开始找合适的位置while (cur){//注意:在平衡二叉搜索树中,键值对pair是按key值进行比较的if (cur->_kv.first < kv.first){cur = cur->_right;parent = cur;}else if (cur->_kv.first > kv.first){cur = cur->_left;parent = cur;}else{return false;//相等直接返回false}}//3.插入结点,注意保持三叉链的链接//此时parent指向待插入结点位置的父节点cur = new Node(kv);if (parent->_kv.first>kv.first){parent->_left = cur;cur->_parent = parent;}else{parent->_right = cur;cur->_parent = parent;}// 1、更新平衡因子while (parent) // parent为空,也就更新到根{// 新增在右,parent->bf++;// 新增在左,parent->bf--;if (cur == parent->_left){parent->_bf--;}else{parent->_bf++;}// 是否继续更新依据:子树的高度是否变化// 1、parent->_bf == 0说明之前parent->_bf是 1 或者 -1// 说明之前parent一边高一边低,这次插入填上矮的那边,parent所在子树高度不变,不需要继续往上更新// 2、parent->_bf == 1 或 -1 说明之前是parent->_bf == 0,两边一样高,现在插入一边更高了,// parent所在子树高度变了,继续往上更新// 3、parent->_bf == 2 或 -2,说明之前parent->_bf == 1 或者 -1,现在插入严重不平衡,违反规则// 就地处理--旋转// 旋转:// 1、让这颗子树左右高度不超过1// 2、旋转过程中继续保持他是搜索树// 3、更新调整孩子节点的平衡因子// 4、让这颗子树的高度跟插入前保持一致if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == -1){cur = parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){// 旋转if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if (parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent);}else{assert(false);}break;}else{assert(false);}}return true;}
private:Node* _root = nullptr;
};
4.AVL树的旋转
在AVL树的插入中,我们提到若是在更新平衡因子的过程当中,出现了平衡因子为-2/2的结点,这时我们需要对以该结点为根结点的树进行旋转处理。平衡二叉搜索树的旋转有多种,分别是左单旋,右单旋,左右双旋,右左双旋,我们分别介绍。
旋转的目的:
- 让这棵树的左右子树高度差的绝对值不超过1
- 旋转过程中依然要保存AVL树的特性
- 更新被调整的结点的平衡因子
- 让这棵子树的高度跟插入当前结点之前的高度一致
左单旋
1.什么情况下进行的是左单旋?
单纯的右边高,当前的parent的平衡因子==2,其右孩子的平衡因子为1,即cur的平衡因子为1的时候进行做单旋。 我们就需要把左边压下来。
if (parent->_bf == 2 && cur->_bf == 1)
{RotateL(parent);
}
2.如何进行左单旋?
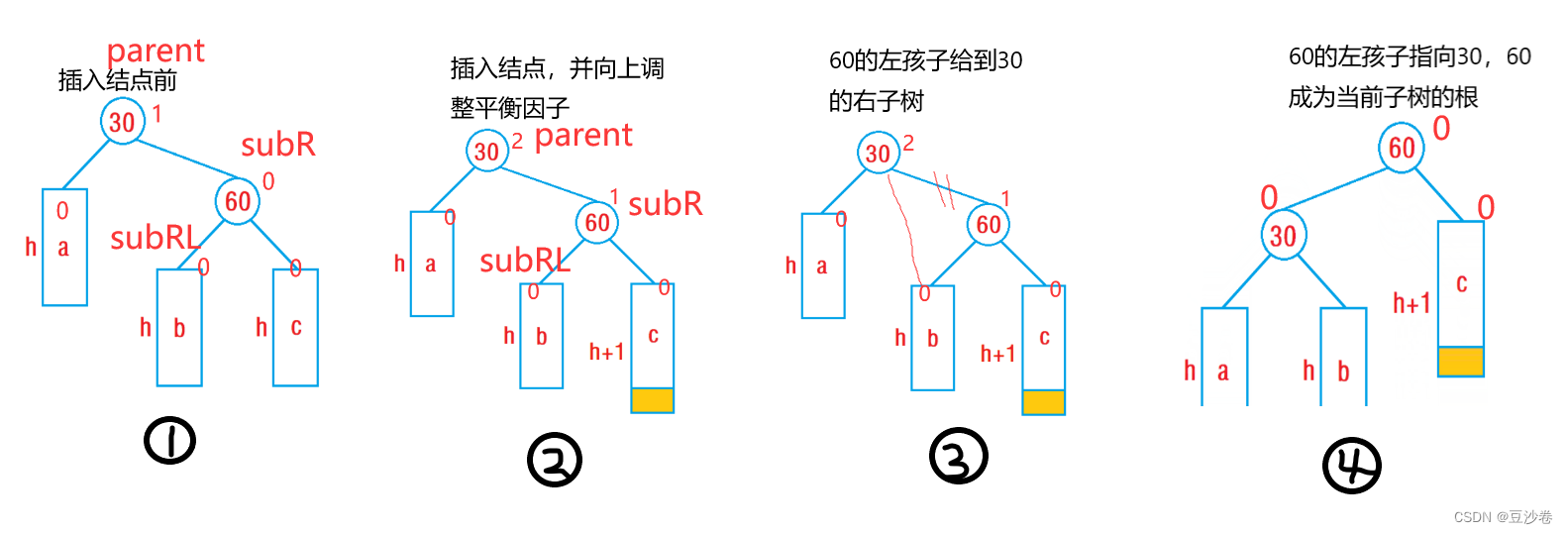
为了提高代码的可阅读性,我们进行一下命名:当前parent指向30,subR(右子树)指向60,subRL(右子树的左子树)指向b。
步骤:
- SubR的左子树作为parent的右子树(这里要注意完善三叉链的连接,勿忘_parent,所以这里有一个注意事项,就是进行subRL->_parent的时候,需要判断subRL是否为空);
- 让parent作为subR的左子树;
- 让subR作为整个子树的根(注意这里要判断subR是子树的根,还是整棵树的root)
- 更新平衡因子。
代码实现:
//左单旋void RotateL(Node* parent){//命名结点Node* subR = parent->_right;Node* subRL = subR->_left;//若parent是某棵子树,则要保留当前结点的父节点,这样旋转之后subR成为根,才能和这棵树连成整体Node* ppNode = parent->_parent;//1.将subR的左子树给到parent的右子树parent->_right = subRL;if (subRL)//注意subRL不为空,才能进行这步,否则会造成对空指针解引用的错误{//完善三叉链的连接subRL->_parent = parent;}//2.将parent给到subR的左子树,subR变成当前子树的根subR->_left = parent;parent->_parent = subR;//3.将旋转完的子树;连接回去if (ppNode == nullptr){//如果ppNode为空,则subR就是当前这棵树的根了_root = subR;subR->_parent = nullptr;}else{//如果刚开始parent是左子树if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}//更新平衡因子parent->_bf = subR->_bf = 0;}
右单旋
1,什么情况下进行右单旋?
单纯的左边高,当前parent的平衡因子== -2,parent左节点的平衡因子等于-1,即cur的平衡因子为-1,我们就需要把右边压下来。
if (parent->_bf == -2 && cur->_bf == -1)
{RotateR(parent);
}
2,如何进行右单旋?
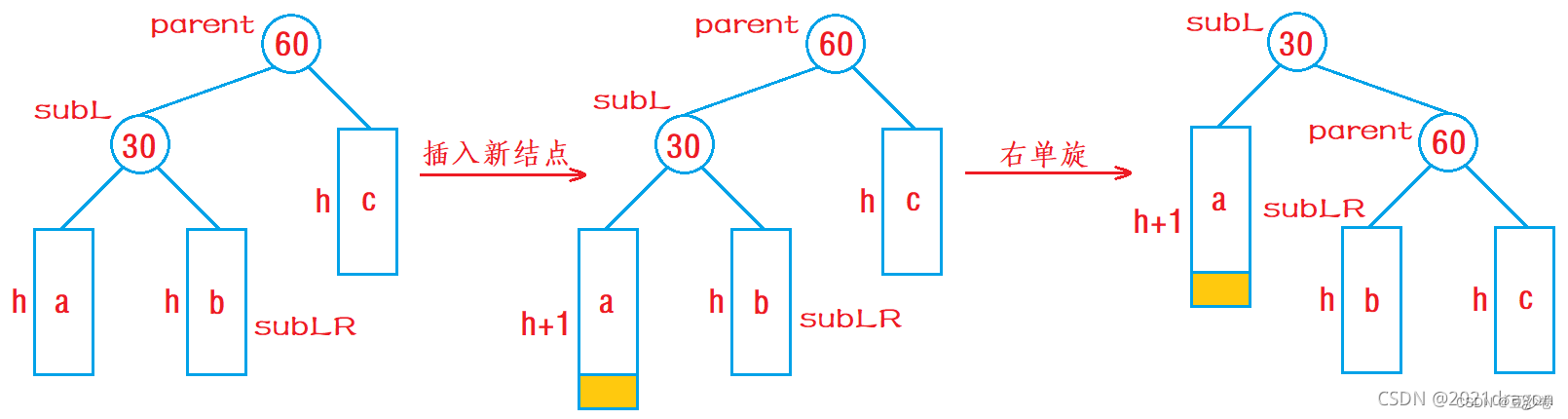
步骤:
- 让subL的右子树作为parent的左子树;
- 让parent作为subL的右子树;
- 让subL作为整个子树的根;
- 更新平衡因子。
void RotateR(Node* parent){//命名结点Node* subL = parent->_left;Node* subLR = subL->_right;//若parent是某棵子树,则要保留当前结点的父节点,这样旋转之后subL成为根,才能和这棵树连成整体Node* ppNode = parent->_parent;//1.将subL的右子树给到parent的左子树parent->_left = subLR;if (subLR)//注意subRL不为空,才能进行这步,否则会造成对空指针解引用的错误{//完善三叉链的连接subLR->_parent = parent;}//2.将parent给到subL的右子树,subL变成当前子树的根subL->_right = parent;parent->_parent = subL;//3.将旋转完的子树;连接回去if (ppNode == nullptr){//如果ppNode为空,则subR就是当前这棵树的根了_root = subL;subL->_parent = nullptr;}else{//如果刚开始parent是左子树if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}//更新平衡因子parent->_bf = subL->_bf = 0;}
左右双旋
1.什么情况下进行左右双旋?
不难发现,前面讲的左单旋和右单旋,它们触发旋转的图形是一条直线,所以当图中出现折线型的路径时,就会触发双旋。
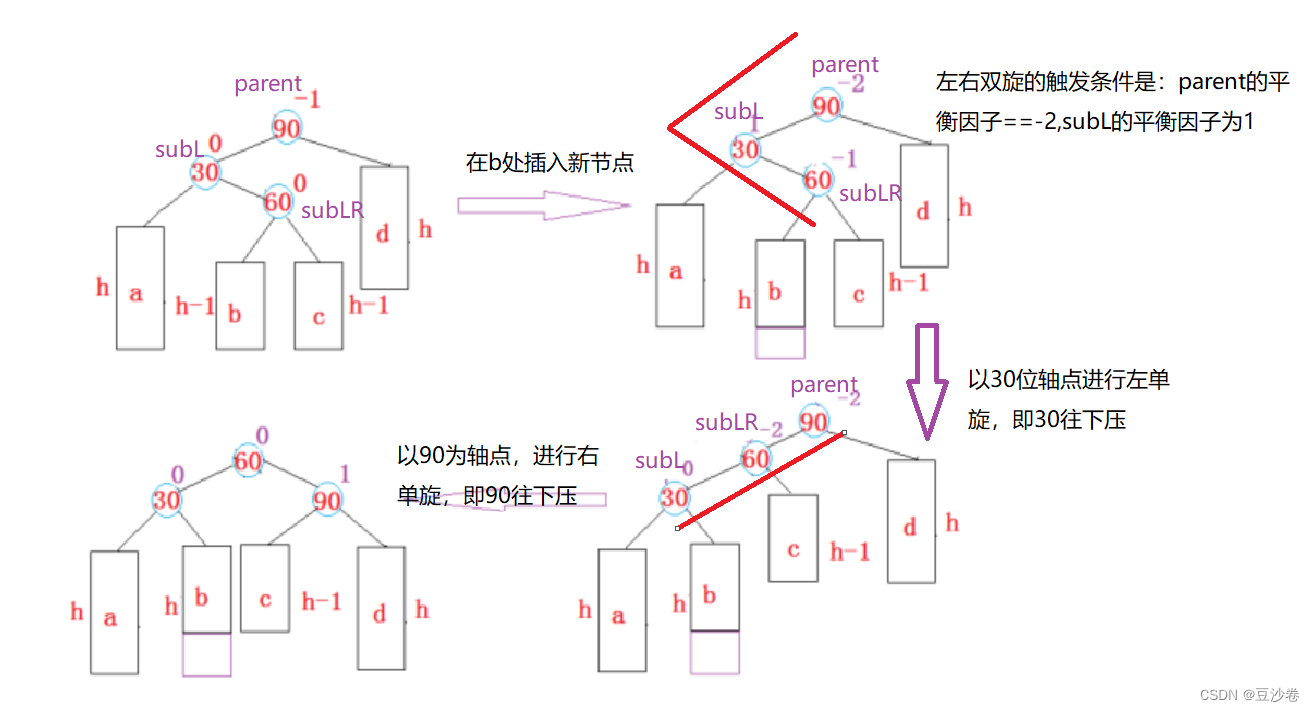
2.如何进行左右双旋?
步骤:
- 以subL为轴点进行左单旋(经过左单旋后,由图可以发现,折线型的路径变成了直线型);
- 以parent为轴点进行右单旋(当出现直线型的路径时,再进行一次单旋即可);
- 更新平衡因子:这是最复杂的一步,我们画的图是在b处插入新的结点,旋转成功后,subL和subLR的平衡因子更新为0,parent的平衡因子变成了1。如果我们是在c处插入新的结点,那么结果又是不同的(这里大家可以自己尝试着换一下旋转过程图)。
左右双旋后,平衡因子的更新随着subLR原始平衡因子的不同分为以下三种情况:
在插入结点后,先记录一下subLR的平衡因子,若平衡因子为-1,则是在b处进行插入,最后subL和subR的平衡因子更新为0,parent的平衡因子变成了1;
若平衡因子为1,则是在c处进行插入,最后subLR和parent的平衡因子更新为0,subL的平衡因子变成了-1;
当subLR原始平衡因子是0时,左右双旋后parent、subL、subLR的平衡因子分别更新为0、0、0。
代码实现:
//左右双旋void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;//以subL为轴点进行左单旋,左边往下压RotateL(parent->_left);//以parent为轴点进行右单旋,右边往下压RotateR(parent);//更新平衡因子if (bf == 1)//subLR右子树新增结点{parent->_bf= 0;subL->_bf = -1;subLR->_bf = 0;}else if (bf == -1){parent->_bf = 1;subL->_bf = 0;subLR->_bf = 0;}else if (bf == 0){parent->_bf = 0;subL->_bf = 0;subLR->_bf = 0;}else{assert(false);}}
右左双旋
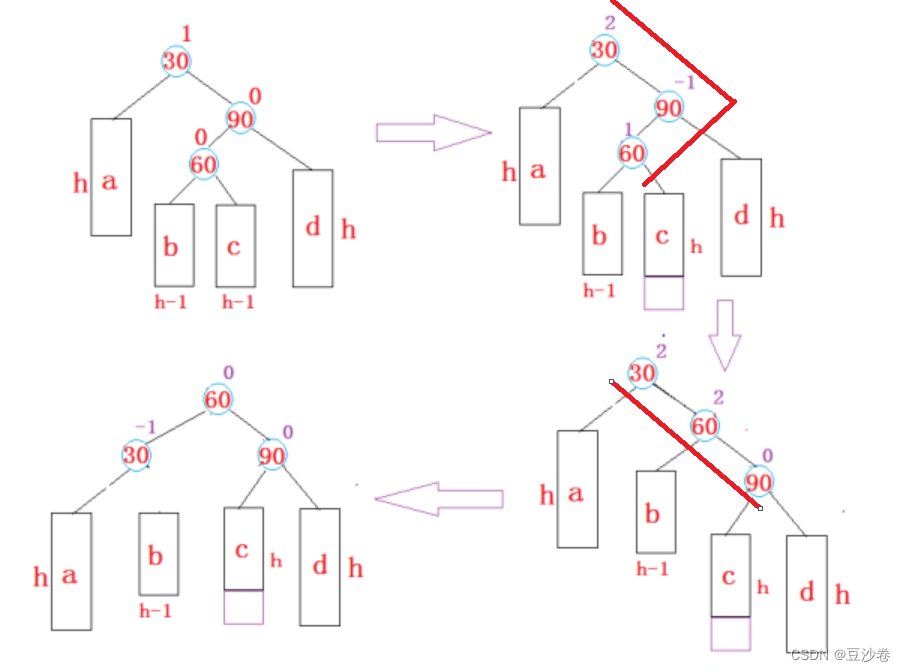
步骤:
- 以subR为旋转点进行右单旋。
- 以parent为旋转点进行左单旋。
- 更新平衡因子。
//右左双旋
void RotateRL(Node* parent)
{Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;//1、以subR为轴进行右单旋RotateR(subR);//2、以parent为轴进行左单旋RotateL(parent);//3、更新平衡因子if (bf == 1){subRL->_bf = 0;parent->_bf = -1;subR->_bf = 0;}else if (bf == -1){subRL->_bf = 0;parent->_bf = 0;subR->_bf = 1;}else if (bf == 0){subRL->_bf = 0;parent->_bf = 0;subR->_bf = 0;}else{assert(false); //在旋转前树的平衡因子就有问题}
}AVL树的验证
AVL树是在二叉搜索树的基础上加入了平衡的限制,因此要验证AVL树,可以分两步:
1.验证其为二叉搜索树
如果中序遍历得到的是一个有序的序列,就说明它是一棵二叉搜索树
2.验证其为平衡树
右子树的高度-左子树的高度绝对值小于等于1
结点的平衡因子是否计算正确
代码实现:
void Inorder(){_Inorder(_root);}void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.first << ":" << root->_kv.second << endl;_Inorder(root->_right);}int Height(Node* root){if (root == nullptr)return 0;int lh = Height(root->_left);int rh = Height(root->_right);return lh > rh ? lh + 1 : rh + 1;}bool IsBalance(){return IsBalance(_root);}bool IsBalance(Node* root){if (root == nullptr){return true;}int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);if (rightHeight - leftHeight != root->_bf){cout << root->_kv.first << "平衡因子异常" << endl;return false;}return abs(rightHeight - leftHeight) < 2&& IsBalance(root->_left)&& IsBalance(root->_right);}
AVL树的删除
可按照二叉搜索树的方式将节点删除,然后再更新平衡因子,最差情况下要一直调整到根节点。
具体实现可参考《算法导论》或《数据结构-用面向对象方法与C++描述》殷人昆版。
AVL树的性能
AVL树是一棵绝对平衡的二叉搜索树,其要求每个结点的左右子树高度差的绝对值小于等于1,这样可以保证访问时的时间复杂度,O(logN),但是如果要对AVL树作一些结构修改的操作,性能就会降低。比如:插入时,我们需要维护其平衡,旋转的次数就比较多,在最差的情况下,还有可能要一直旋转到根。因此,如果需要一直查询高效且有序的数据结构,而且数据的个数是不变的,可以考虑AVL树,但如果一个结构经常需要修改,就不适合用AVL树。
相关文章:

【C++】AVL树,平衡二叉树详细解析
文章目录前言1.AVL树的概念2.AVL树节点的定义3.AVL树的插入4.AVL树的旋转左单旋右单旋左右双旋右左双旋AVL树的验证AVL树的删除AVL树的性能前言 前面对map/multimap/set/multiset进行了简单的介绍,在其文档介绍中发现,这几个容器有个共同点是࿱…...
C/C++开发,无可避免的多线程(篇四).线程与函数的奇妙碰撞
一、函数、函数指针及函数对象 1.1 函数 函数(function)是把一个语句序列(函数体, function body)关联到一个名字和零或更多个函数形参(function parameter)的列表的 C 实体,可以通过返回或者抛…...

elisp简单实例: taglist
从vim 转到emacs 下,一直为缺少vim 中的tablist 插件而感到失落. 从网上得到的一个emacs中的taglist, 它的功能很简陋,而且没有任何说明, 把它做为elisp的简单实例,供初学者入门倒不错,我给它加了很多注释,帮助理解, 说实话,感觉这百行代码还是挺有深度的,慢慢体会,调试才会有收…...
-认知服务(3))
Azure AI基础到实战(C#2022)-认知服务(3)
目录 OpenFileDialog 类上一节代码的API剖析ComputerVisionClientExtensions.ReadAsync MethodReadHeaders ClassReadHeaders.OperationLocation Property探索ReadHeaders加上调试代码可用于 Azure 认知服务的身份验证标头使用单服务订阅密钥进行身份验证使用多服务订阅密钥进行…...
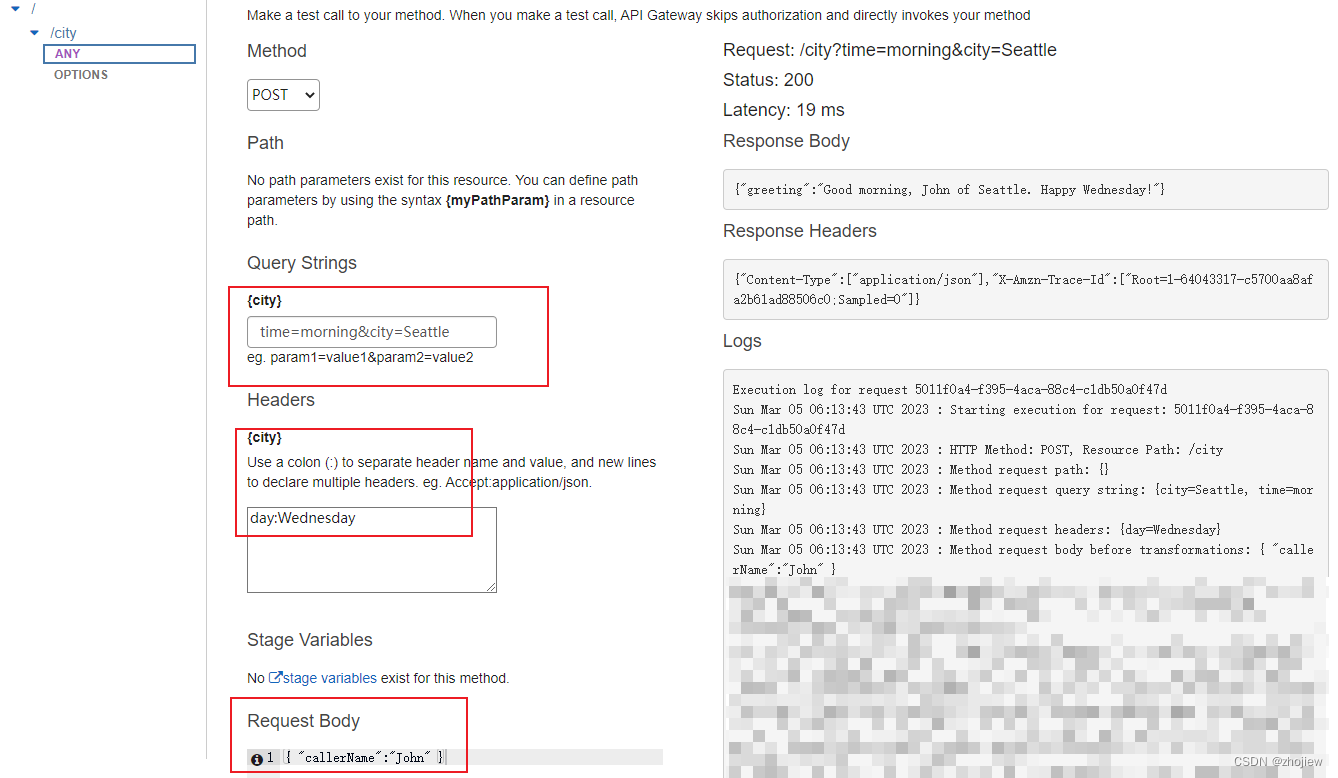
aws apigateway 使用restapi集成lambda
参考资料 代理集成,https://docs.aws.amazon.com/zh_cn/apigateway/latest/developerguide/api-gateway-create-api-as-simple-proxy-for-lambda.html非代理集成,https://docs.aws.amazon.com/zh_cn/apigateway/latest/developerguide/getting-started-…...
HTML基础
HTML 基础 文章目录HTML 基础列表标签无序列表有序列表自定义列表表格标签表格基本标签表格基本结构表格完整结构:合并行和合并列表单标签input 系列标签属性标签text 标签radio 标签 单选框file 标签 文件选择button 标签 按钮input系列标签总结button按钮标签sele…...

ThreadPoolExecutor参数 keepAliveTime allowCoreThreadTimeOut
/*** Timeout in nanoseconds for idle threads waiting for work.* Threads use this timeout when there are more than corePoolSize* present or if allowCoreThreadTimeOut. Otherwise they wait* forever for new work.*/ private volatile long keepAliveTime;等待工作的…...

什么是Hibernate框架?
简单介绍:Hibernate框架是当今主流的java持久层框架之一,是一个开放源码的ORM(Object Relational Mapping,对象关系映射)框架,它对JDBC进行了轻量级的封装,使得JAVA开发人员可以使用面向对象的编…...

指针面试笔试题练习
前言 🎈个人主页:🎈 :✨✨✨初阶牛✨✨✨ 🐻推荐专栏: 🍔🍟🌯 c语言进阶 🔑个人信条: 🌵知行合一 🍉本篇简介:>:介绍c语言中有关指针更深层的知识. 金句分享: ✨星光…...

docker(三)仓库的搭建、官方私有仓库的加密和认证
文章目录一、docker仓库二、仓库Registry工作原理三、搭建本地私有仓库四、配置镜像加速器五、私有仓库的加密认证1.非加密下上传拉取2.insecure registry3.仓库加密4.仓库认证一、docker仓库 什么是仓库 Docker 仓库是用来包含镜像的位置,Docker提供一个注册服务器…...

FPGA实现SDI视频编解码 SDI接收发送,提供2套工程源码和技术支持
目录1、前言2、设计思路和框架SDI接收SDI缓存写方式处理SDI缓存读方式处理SDI缓存的目的SDI发送3、工程1详解4、工程2详解5、上板调试验证并演示6、福利:工程代码的获取1、前言 FPGA实现SDI视频编解码目前有两种方案: 一是使用专用编解码芯片࿰…...

Android 基础知识4-3.5 RadioButton(单选按钮)Checkbox(复选框)详解
一、RadioButton(单选按钮) 1.1、简介 RadioButton表示单选按钮,是button的子类,每一个按钮都有选择和未选中两种状态,经常与RadioGroup一起使用,否则不能实现其单选功能。RadioGroup继承自LinearLayout&a…...

用代码实现解析解的方式求解_梯度下降法思路_导函数有什么用_接23节---人工智能工作笔记0026
这里24节,25节,介绍了一下人工智能高等数学要学习的一些内容,初步了解了一下,微积分中用到的知识~微分~以及导数这里... 然后接着23节,我们还是继续,走人工智能的主线,先把整体的人工智能的内容学习一遍,然后再去回去看数学知识更有目的性. 然后首先来回顾一下,这里机器学习,其…...
大数据ETL开发之图解Kettle工具
详细笔记参考:https://blog.csdn.net/yuan2019035055/article/details/120409547以下只是简单记录一下我学习过程中的心得3.1.5 JSON输入JSONPath 类似于 XPath 在 xml 文档中的定位,JsonPath 表达式通常是用来路径检索或设置Json的。其表达式可以接受“…...

docker-容器数据卷
Docker挂载主机目录访问如果出现cannot open directory.:Permission denied 解决办法:在挂载目录后多加一个--privileged=true参数即可; 一、介绍 卷就是目录或文件,存在于一个或多个容器中,由docker挂载到容器,但不属于联合文件系统,因此能绕过Union Fil…...
【C++】类和对象补充知识点
🏖️作者:malloc不出对象 ⛺专栏:C的学习之路 👦个人简介:一名双非本科院校大二在读的科班编程菜鸟,努力编程只为赶上各位大佬的步伐🙈🙈 目录前言一、再谈构造函数1.1 构造函数体赋…...
路径规划-人工势场法
一.基本思想 目标点对机器人产生吸引力,障碍物对机器人产生排斥力; 所有力的合成构成机器人的控制律 二. 主要步骤 1.构建人工势场 目标点:吸引势场 障碍物:排斥势场 2.根据人工势场计算力 对势场求偏导 3.计算合力 计…...
20230304学习笔记
1、Mybatis #{}和${}的区别是什么 a、#{}是预编辑处理、是占位符,${}是字符串拼接符。 b、#{}替换为?号,用PreparedStatement来赋值,${}直接替换变量的值,用Statement赋值。 c、#{}在DBMS中、自动加入单引号&#…...

[数据集][VOC][目标检测]河道垃圾水面漂浮物数据集目标检测可用yolo训练-1304张介绍
数据集格式:Pascal VOC格式(不包含分割路径的txt文件和yolo格式的txt文件,仅仅包含jpg图片和对应的xml) 图片数量(jpg文件个数):1304 标注数量(xml文件个数):1304 标注类别数:1 标注类别名称:["trash"] …...

JavaWeb--JSP案例
JSP案例8 案例8.1 环境准备8.1.1 创建工程8.1.2 创建包8.1.3 创建表8.1.4 创建实体类8.1.5 准备mybatis环境8.2 查询所有8.2.1 编写BrandMapper8.2.2 编写工具类8.2.3 编写BrandService8.2.4 编写Servlet8.2.5 编写brand.jsp页面8.2.6 测试8.3 添加8.3.1 编写BrandMapper方法8.…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

CppCon 2015 学习:Reactive Stream Processing in Industrial IoT using DDS and Rx
“Reactive Stream Processing in Industrial IoT using DDS and Rx” 是指在工业物联网(IIoT)场景中,结合 DDS(Data Distribution Service) 和 Rx(Reactive Extensions) 技术,实现 …...
