DT DAY3 信号和槽
作业:
1> 思维导图
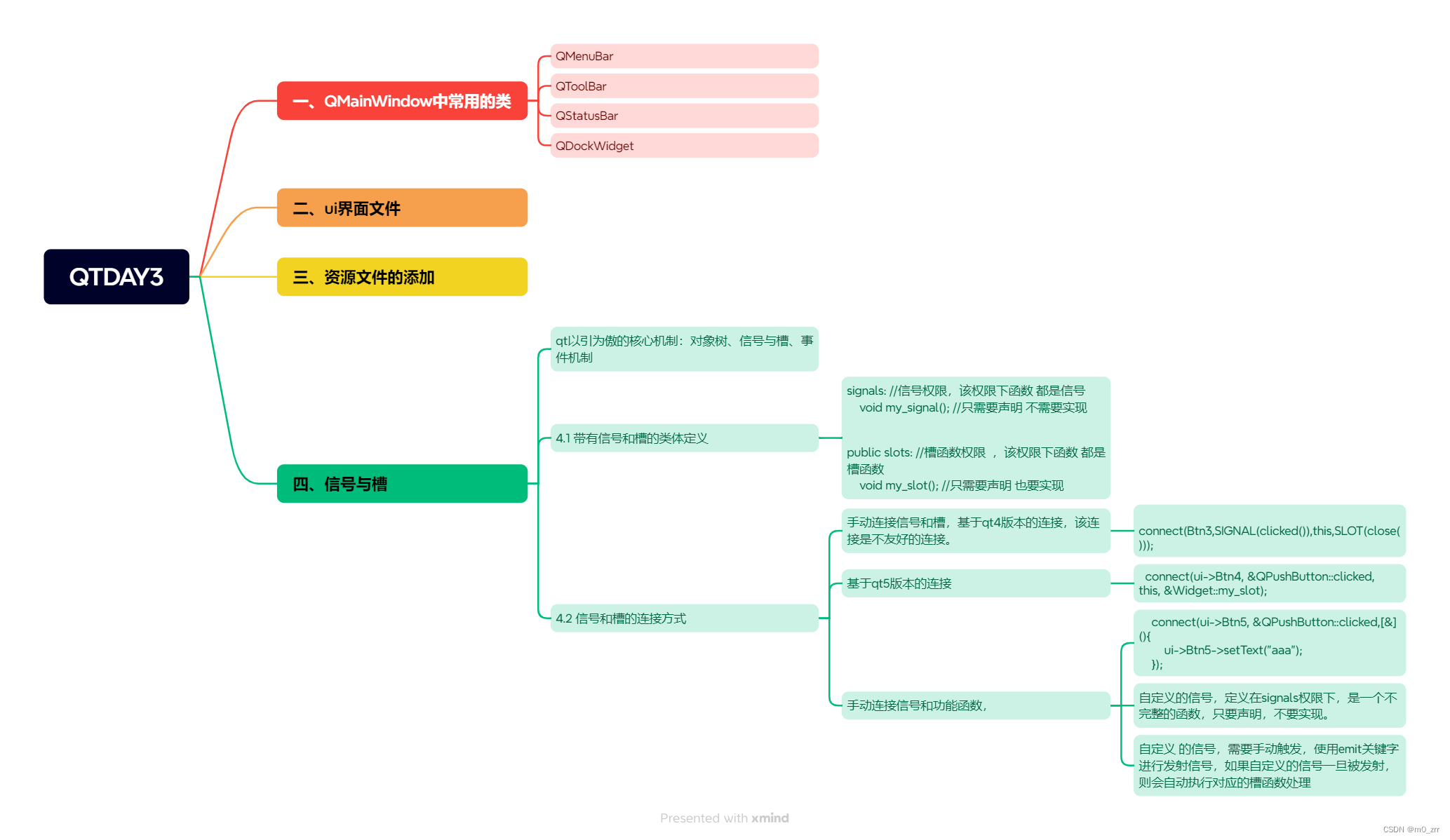
2>
使用手动连接,将登录框中的取消按钮使用qt4版本的连接到自定义的槽函数中,在自定义的槽函数中调用关闭函数
btn3= new QPushButton("按钮3",this);btn3->resize(ui->btn2->width(),ui->btn2->height());btn3->move(ui->btn2->x(),ui->btn2->y()+ui->btn2->height()+10);//手动连接3connect(btn3,SIGNAL(clicked()),this,SLOT(close()))将登录按钮使用qt5版本的连接到自定义的槽函数中,在槽函数中判断ui界面上输入的账号是否为"admin",密码是否为"123456",如果账号密码匹配成功,则输出“登录成功”,并关闭该界面,如果匹配失败,则输出登录失败,并将密码框中的内容清空
connect(ui->btn6,&QPushButton::clicked,this,&Widget::my_slot);});void Widget::my_slot()
{ if(ui->lineEdit=="admin"&& ui->lineEdit_2=="123456"){qDebug() << "login success";//窗口关闭this->close(); } else{qDebug() << "login fail";// 清空ui->lineEdit_2->clear(); }}
Widget::~Widget()
{delete ui;
}相关文章:

DT DAY3 信号和槽
作业: 1> 思维导图 2> 使用手动连接,将登录框中的取消按钮使用qt4版本的连接到自定义的槽函数中,在自定义的槽函数中调用关闭函数 btn3 new QPushButton("按钮3",this);btn3->resize(ui->btn2->width(),ui->b…...

Spring、SpringBoot、SpringCloud三者的区别
Spring、Spring Boot 和 Spring Cloud 是构建企业级 Java 应用程序的不同层次的框架和工具。下面详细介绍它们之间的区别: 1. Spring框架: 概述: Spring 是一个全功能的企业级 Java 框架,提供了依赖注入、面向切面编程、事务管理…...
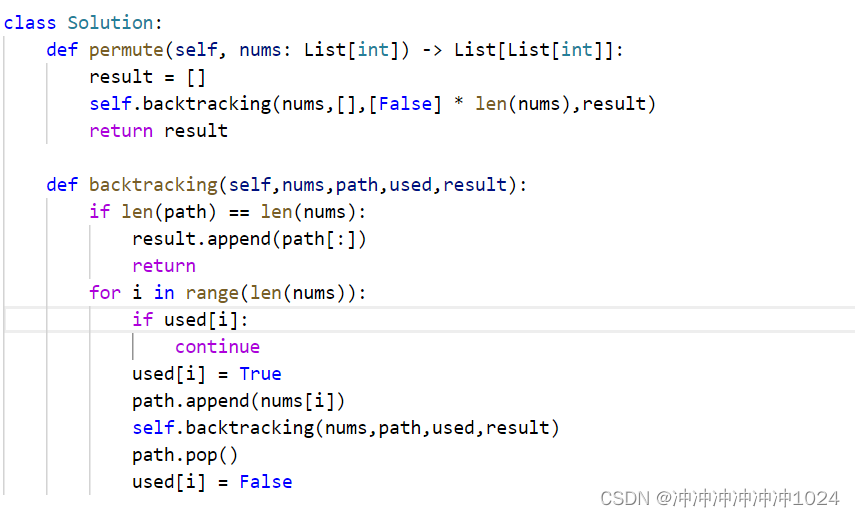
leetcode:46.全排列
1.什么是排列? 有顺序!! 2.树形结构: 使用used数组进行标记取过的元素,一个元素一个元素地进行取值,取完之后将used数组进行标记。 3.代码实现:(循环从i0开始,而不是…...

基于STM32的宠物箱温度湿度监控系统
基于STM32的宠物箱温度湿度监控系统 一、引言 随着人们生活水平的提高,养宠物已经成为越来越多人的选择。宠物作为家庭的一员,其生活环境和健康状况受到了广泛关注。温度和湿度是影响宠物舒适度和健康的重要因素之一。因此,开发一款能够实时监控宠物箱温度和湿度的系统具有…...

《高质量的C/C++编程规范》学习
目录 一、编程规范基础知识 1、头文件 2、程序的板式风格 3、命名规则 二、表达式和基本语句 1、运算符的优先级 2、复合表达式 3、if语句 4、循环语句的效率 5、for循环语句 6、switch语句 三、常量 1、#define和const比较 2、常量定义规则 四、函数设计 1、参…...
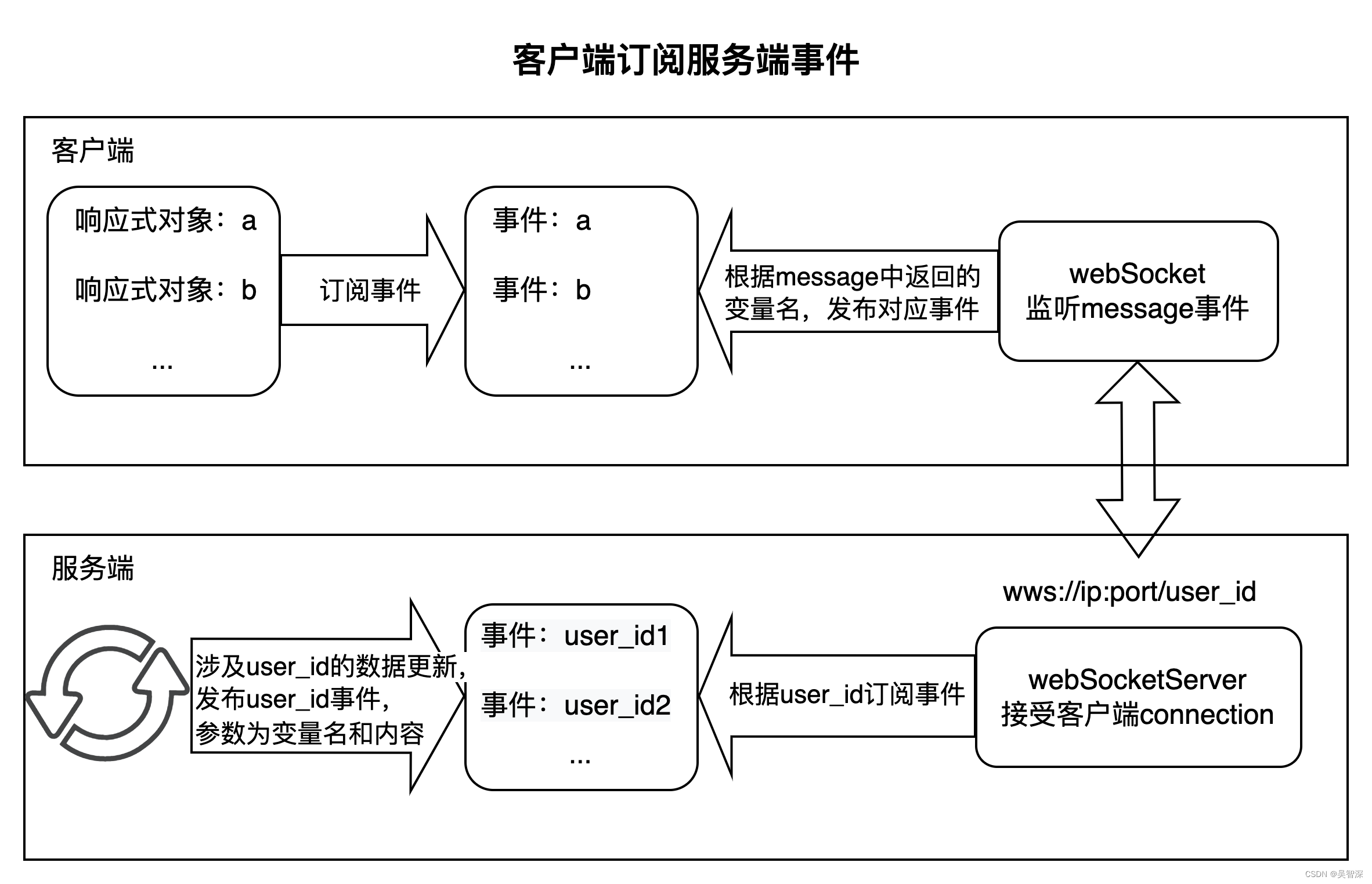
客户端订阅服务端事件的机制
一、场景描述 产业大脑平台是一个典型的审核系统,用户发布到平台的信息需要经过审核员审核后生效。 用户发布信息->审核员审核信息->用户信息生效,这一流程可能发生在用户的同一次登录周期内。为了使客户端能实时响应信息的状态变化,…...
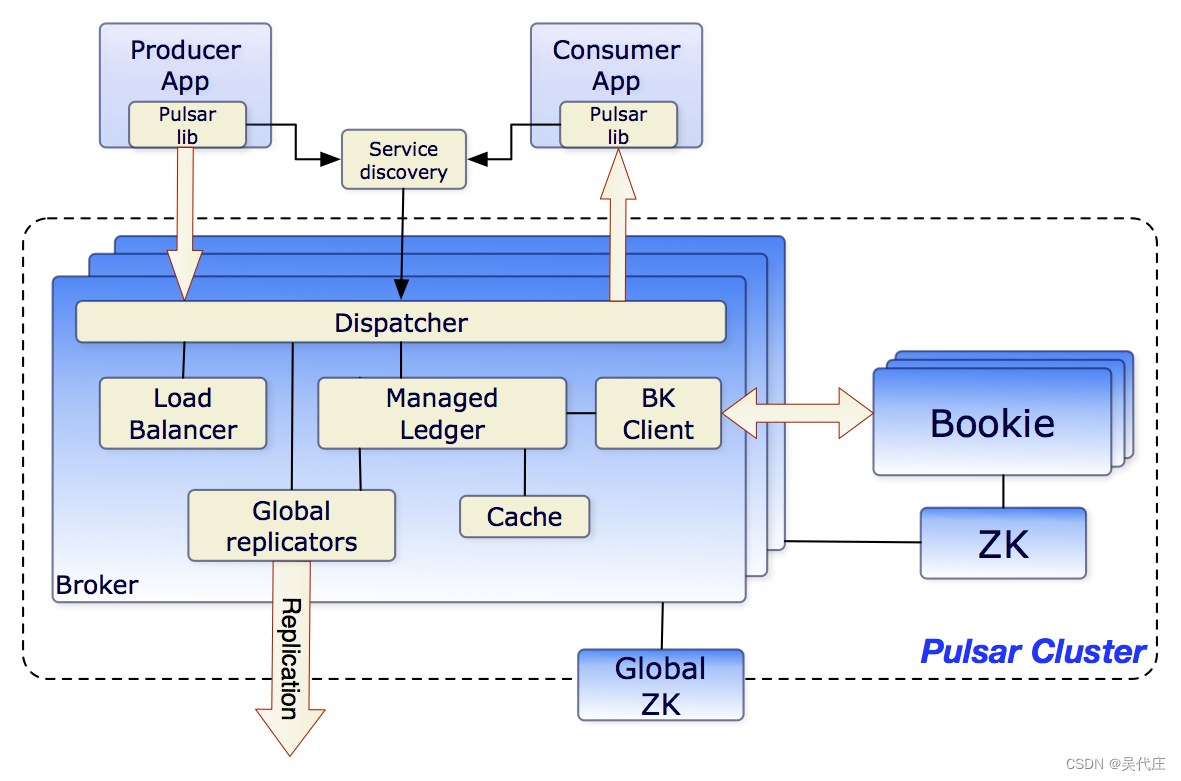
pulsar入门介绍
概述 Pulsar 是一个多租户、高性能的服务器到服务器消息传递解决方案。Pulsar 最初由 Yahoo 开发,由 Apache 软件基金会管理。 特点 Pulsar 的主要功能如下: 原生支持 Pulsar 实例中的多个集群,可跨集群无缝地复制消息。非常低的发布和端…...

Leetcode 3047. Find the Largest Area of Square Inside Two Rectangles
Leetcode 3047. Find the Largest Area of Square Inside Two Rectangles 1. 解题思路2. 代码实现 题目链接:3047. Find the Largest Area of Square Inside Two Rectangles 1. 解题思路 这道题倒是没啥特别的思路,直接暴力求解就是了,因此…...
ELK 简介安装
1、概念介绍 日志介绍 日志就是程序产生的,遵循一定格式(通常包含时间戳)的文本数据。 通常日志由服务器生成,输出到不同的文件中,一般会有系统日志、 应用日志、安全日志。这些日志分散地存储在不同的机器上。 日志…...
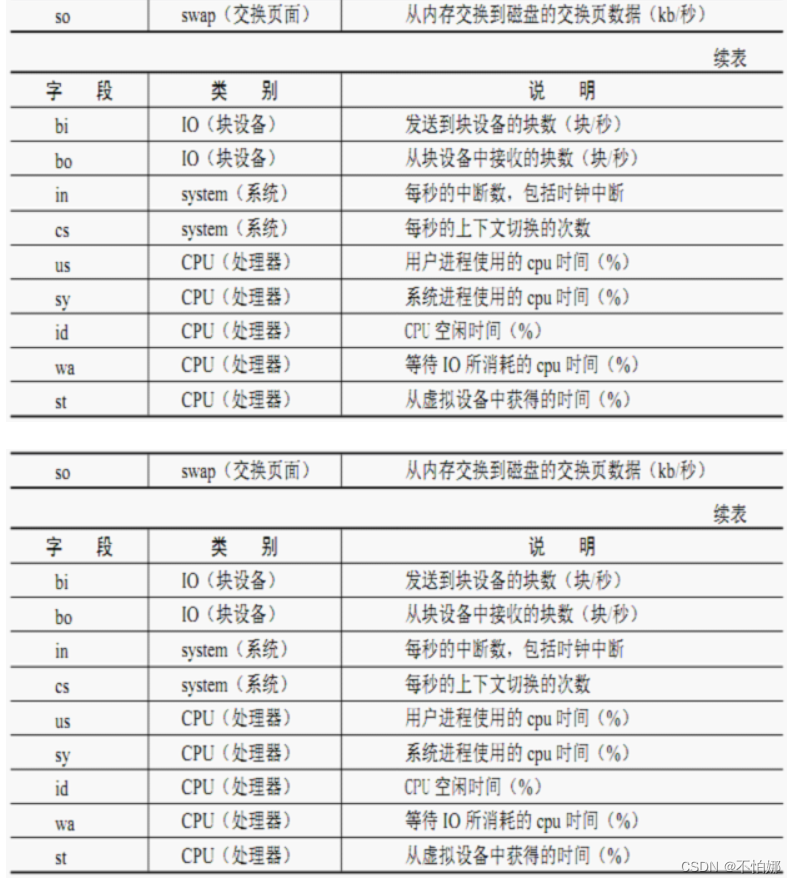
Linux 的交换空间(swap)是什么?有什么用?
目录 swap是什么?swap有什么用?swap使用典型场景如何查看你的系统是否用到交换空间呢?查看系统中swap in/out的情况 swap是什么? swap就是磁盘上的一块区域。它和Windows系统中的交换文件作用类似,但是它是一段连续的…...
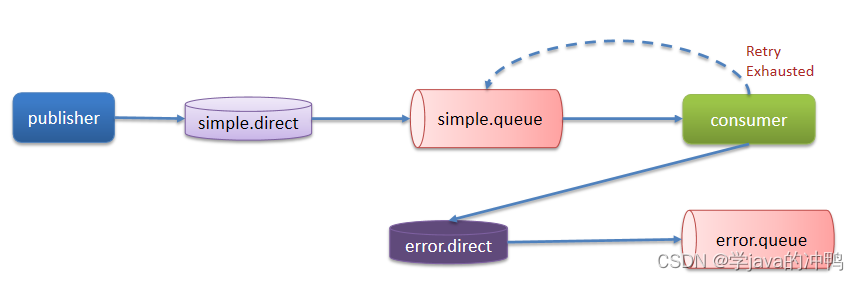
消息中间件篇之RabbitMQ-消息不丢失
一、生产者确认机制 RabbitMQ提供了publisher confirm机制来避免消息发送到MQ过程中丢失。消息发送到MQ以后,会返回一个结果给发送者,表示消息是否处理成功。 当消息没有到交换机就失败了,就会返回publish-confirm。当消息没有到达MQ时&…...

MongoDB中的TTL索引:自动过期数据的深入解析与使用方式
目录 一、TTL索引的深入原理二、TTL索引的使用方式三、TTL索引的限制与考虑因素四、优化TTL索引的策略五、总结 一、TTL索引的深入原理 TTL(Time-To-Live)索引在MongoDB中是一种特殊的索引,用于自动删除过期的文档。其核心原理在于MongoDB会…...

IPV6地址
技术背景:对IPV4做优化,比如地址长度128,简化了报文头部---快 ipv6地址 十六进制,简写前导0忽略,连续的0写成:: IPv6地址类型 1.单播 2.组播---接口有地址后,自动加入到一个组播里 3.任播---允许地址…...
解密API关键词搜索(淘宝京东1688)商品列表数据
API关键词搜索商品列表数据:赋能电商行业的新动力 随着电子商务的蓬勃发展,API(应用程序接口)关键词搜索商品列表数据在电商行业中的重要性日益凸显。这一数据资源不仅为消费者提供了便捷的购物体验,还为电商企业带来…...
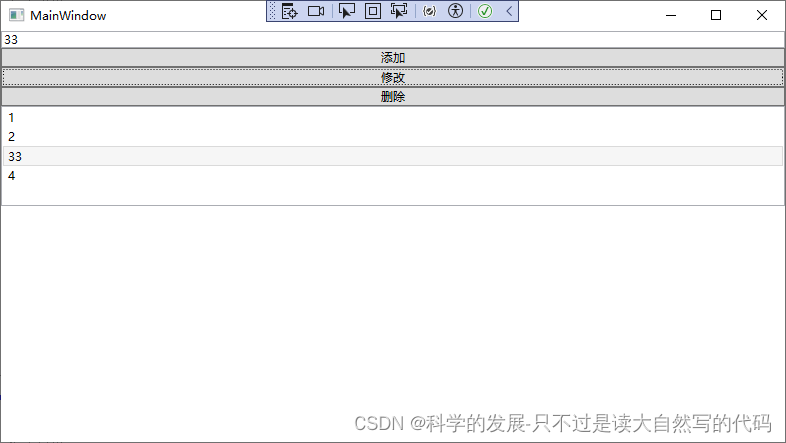
wpf 简单实验 数据更新 列表更新
1.概要 1.1 需求 一个列表提供添加修改删除的功能,添加和修改的内容都来自一个输入框 1.2 要点 DisplayMemberPath"Zhi"列表.ItemsSource datalist;(列表.SelectedItem ! null)(列表.SelectedItem as A).Zhi 内容.Text;datalist.Remove((列表.Selec…...
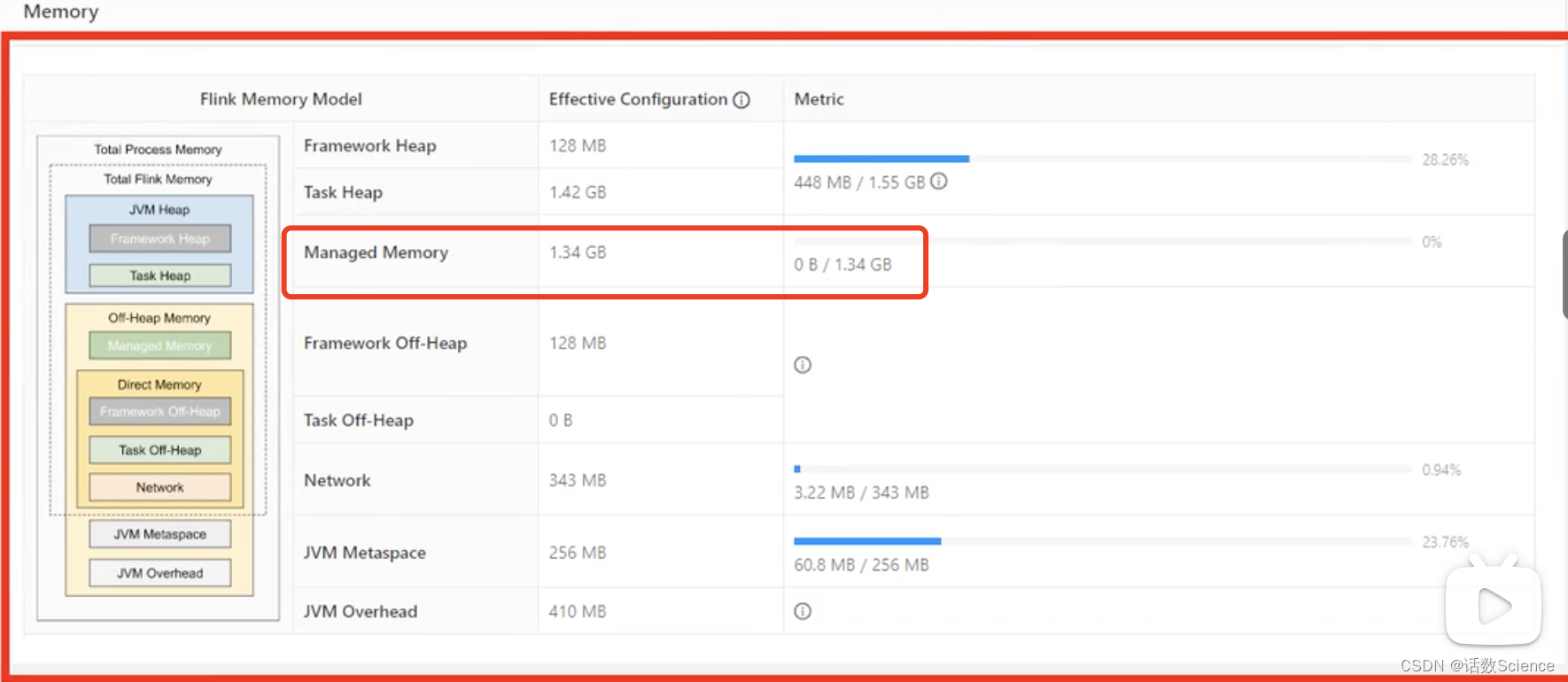
【Flink精讲】Flink性能调优:内存调优
内存调优 内存模型 JVM 特定内存 JVM 本身使用的内存,包含 JVM 的 metaspace 和 over-head 1) JVM metaspace: JVM 元空间 taskmanager.memory.jvm-metaspace.size,默认 256mb 2) JVM over-head 执行开销࿱…...
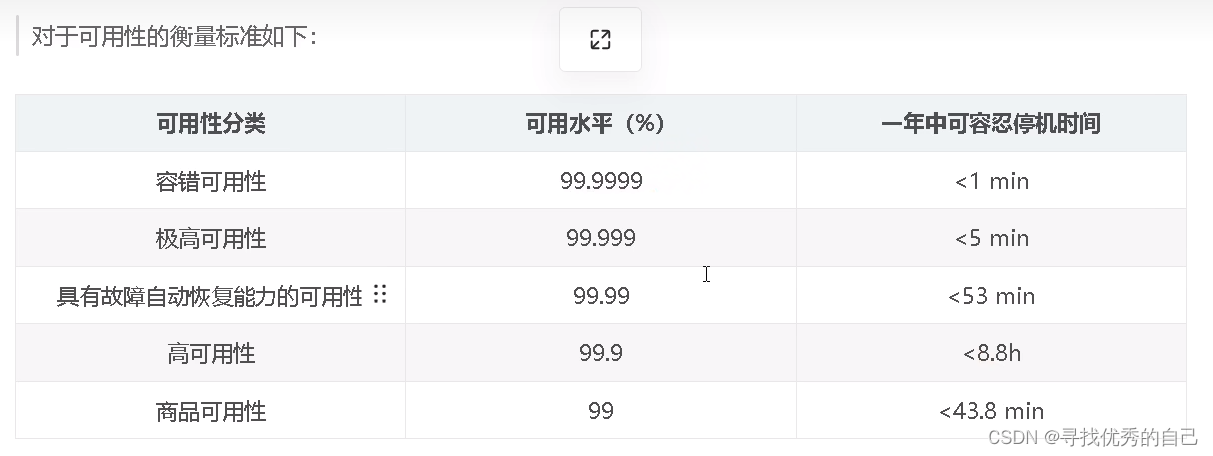
Java 中常用的数据结构类 API
目录 常用数据结构API 对应的线程安全的api 高可用衡量标准 常用数据结构API ArrayList: 实现了动态数组,允许快速随机访问元素。 import java.util.ArrayList; LinkedList: 实现了双向链表,适用于频繁插入和删除操作。 import java.util.LinkedLis…...
基本数据结构(数组,字符串))
JavaScript学习小记(1)基本数据结构(数组,字符串)
一个寒假确实过的很快,这个寒假除了调包调参突然心血来潮想学一下前端,学习过程比较平滑,我是自己找的技术文档+写代码实践来学习的,教程视频虽然详细,但是真的一点都看不动。 目录 JS如何定义变量的老旧的…...

python opencv实现车牌识别
目录 一:实现步骤: 二:实现车牌检测 一:实现步骤: 使用Python和OpenCV实现车牌识别的步骤大致可以分为以下两部分: 车牌检测: 读取需要进行车牌识别的图片。 对图像进行灰度化处理,可能还包括高斯模糊和灰度拉伸。 进行开运算,消除图像中的噪声。 将灰度拉伸后的图…...
)
K8S节点GPU虚拟化(vGPU)
vGPU实现方案 4paradigm提供了k8s-device-plugin,该插件基于NVIDIA官方插件(NVIDIA/k8s-device-plugin),在保留官方功能的基础上,实现了对物理GPU进行切分,并对显存和计算单元进行限制,从而模拟出多张小的vGPU卡。在k8s集群中,基于这些切分后的vGPU进行调度,使不同的容器…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...
