【GPTs分享】GPTs分享之Write For Me
Write For Me 是一个专门定制的GPT版本,旨在为用户提供高质量的文本内容创作服务。它适用于各种写作需求,从商业计划、学术文章到创意故事等。下面是从简介、主要功能、使用案例、优点和局限性几个方面对Write For Me 的详细介绍。
简介
Write For Me 是一个基于人工智能的写作助手,通过深度学习算法训练而成,旨在帮助用户高效地生成各种类型的文本内容。它理解用户的具体需求,包括内容的目的、目标受众、语调、字数限制、风格和格式,并据此定制内容。
主要功能
- 需求理解:Write For Me 能够询问并理解用户关于预期用途、目标受众、语调、字数、风格和格式的具体需求。
- 创建大纲:根据用户需求,它能创建详细的内容大纲,为每个部分提供概要和字数分配。
- 字数管理:在写作过程中,Write For Me 会跟踪字数,确保内容遵守用户的规定,并在各部分间平滑过渡。
- 创意扩展:它使用多种策略如扩展讨论、加入要点列表和有趣的事实来丰富内容,同时保持相关性和质量。
- 分步写作与交付:Write For Me 分步骤编写并交付内容,向用户更新进展并为后续部分做计划。
- 内容质量:它融合SEO策略,专注于使内容吸引人,并适合预定的受众和平台。
- 内容格式化:Write For Me 默认使用Markdown格式,但可以按需调整为任何格式。
使用案例
- 商业写作:为营销材料、商业计划或网站内容创作。
- 学术写作:帮助撰写研究论文、报告或文献综述。
- 创意写作:创作故事、剧本或诗歌。
- 内容营销:撰写博客文章、新闻稿或社交媒体帖子。
优点
- 效率:Write For Me 能够快速生成高质量的内容草稿,节省用户时间。
- 灵活性:它适应各种写作任务和风格要求。
- 创造性:提供创新的内容创意和构思。
- 用户友好:提供易于理解和操作的界面。
局限性
- 人工智能局限:尽管 Write For Me 能提供高质量的内容,但其理解和创造力受限于当前的AI技术水平。
- 个性化:需要足够的信息才能产出高度个性化的内容。
- 复杂主题理解:在处理高度专业化或复杂的主题时,可能需要更多的指导和校正。
体验链接
https://chat.openai.com/g/g-B3hgivKK9-write-for-me
示例




相关文章:

【GPTs分享】GPTs分享之Write For Me
Write For Me 是一个专门定制的GPT版本,旨在为用户提供高质量的文本内容创作服务。它适用于各种写作需求,从商业计划、学术文章到创意故事等。下面是从简介、主要功能、使用案例、优点和局限性几个方面对Write For Me 的详细介绍。 简介 Write For Me …...

css4浮动+清除浮动
浮动 一.常见网页布局1.三种布局方式2.布局准则 二.浮动(float)1.好处2.概念3.三大特性4.使用5.常见网页布局模板6.注意点 三.清除浮动1.why2.本质3.语法4.四种way(后三个都是给父级添加)清除浮动总结 一.常见网页布局 1.三种布局…...
外包干了3个月,技术倒退明显...
先说情况,大专毕业,18年通过校招进入湖南某软件公司,干了接近6年的功能测试,今年年初,感觉自己不能够在这样下去了,长时间呆在一个舒适的环境会让一个人堕落!而我已经在一个企业干了四年的功能测试…...
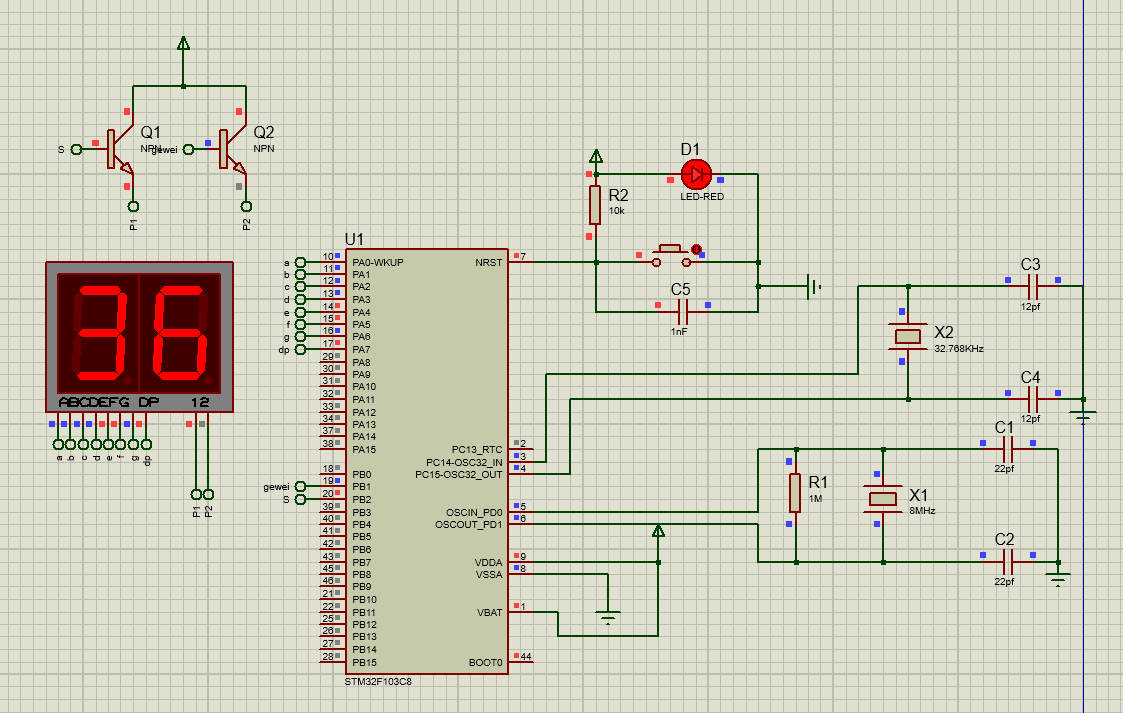
STM32控制数码管从0显示到99
首先 先画电路图吧!打开proteus,导入相关器件,绘制电路图。如下:(记得要保存啊!发现模拟一遍程序就自动退出了,有bug,我是解决不了,所以就是要及时保存,自己重…...

【机器学习算法】KNN鸢尾花种类预测案例和特征预处理。全md文档笔记(已分享,附代码)
本系列文章md笔记(已分享)主要讨论机器学习算法相关知识。机器学习算法文章笔记以算法、案例为驱动的学习,伴随浅显易懂的数学知识,让大家掌握机器学习常见算法原理,应用Scikit-learn实现机器学习算法的应用࿰…...
Windows 自带的 Linux 子系统(WSL)安装与使用
WSL官网安装教程: https://learn.microsoft.com/zh-cn/windows/wsl/install Windows 自带的Linux子系统,比用VM什么的香太多了。可以自己看官方教程,也可以以下步骤完成。 如果中间遇到我没遇到的问题百度,可以在评论区评论&#…...

C语言--贪吃蛇
目录 1. 实现目标2. 需掌握的技术3. Win32 API介绍控制台程序控制台屏幕上的坐标COORDGetStdHandleGetConsoleCursorinfoCONSOLE_CURSOR_INFOSetConsoleCursorInfoSetConsoleCursorPositionGetAsyncKeyState 4. 贪吃蛇游戏设计与分析地图<locale.h>本地化类项setlocale函…...
原型设计工具Axure RP
Axure RP是一款专业的快速原型设计工具。Axure(发音:Ack-sure),代表美国Axure公司;RP则是Rapid Prototyping(快速原型)的缩写。 下载链接:https://www.axure.com/ 下载 可以免费试用…...

HeadFirst读书笔记
一、设计模式入门 1、使用模式最好的方式“把模式装进脑子里,然后在你的设计和已有的应用中,寻找何处可以使用它们”。以往是代码复用,现在是经验复用。 2、软件开发的一个不变的真理就是变化。 二、设计原则 1、找出应用中可能需要变化之…...

【C++】---内存管理new和delete详解
一、C/C内存分布 C/C内存被分为6个区域: (1) 内核空间:存放内核代码和环境变量。 (2)栈区:向下增长(存放非静态局部变量,函数参数,返回值等等) …...

go-zero微服务入门教程
go-zero微服务入门教程 本教程主要模拟实现用户注册和用户信息查询两个接口。 准备工作 安装基础环境 安装etcd, mysql,redis,建议采用docker安装。 MySQL安装好之后,新建数据库dsms_admin,并新建表sys_user&#…...

蓝桥杯刷题--python-12
3768. 字符串删减 - AcWing题库 nint(input()) sinput() res0 i0 while(i<n): if s[i]x: ji1 while(j<n and s[j]x): j1 resmax(j-i-2,0) ij else: i1 print(res) 3777. 砖块 - AcWing题库 # https://www.a…...

LeetCode LCR 085.括号生成
正整数 n 代表生成括号的对数,请设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。 示例 1: 输入:n 3 输出:[“((()))”,“(()())”,“(())()”,“()(())”,“()()()”] 示例 2: 输入&#x…...
抖音视频评论数据提取软件|抖音数据抓取工具
一、开发背景: 在业务需求中,我们经常需要下载抖音视频。然而,在网上找到的视频通常只能通过逐个复制链接的方式进行抓取和下载,这种操作非常耗时。我们希望能够通过关键词自动批量抓取并选择性地下载抖音视频。因此,为…...

【web】云导航项目部署及环境搭建(复杂)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、项目介绍1.1项目环境架构LNMP1.2项目代码说明 二、项目环境搭建2.1 Nginx安装2.2 php安装2.3 nginx配置和php配置2.3.1 修改nginx文件2.3.2 修改vim /etc/p…...

软件测试人员必会的linux命令
文件和目录操作: ● ls:列出目录中的文件和子目录。 ● cd:改变当前工作目录。 ● mkdir:创建新目录。 ● rm:删除文件或目录。 ● cp:复制文件或目录。 ● mv:移动或重命名文件或目录。 文本查看和编辑: ● cat:查看文件内容。 ● more或less:分页查看文件内…...

Mac使用K6工具压测WebSocket
commend空格 打开终端,安装k6 brew install k6验证是否安装成功 k6 version设置日志级别为debug export K6_LOG_LEVELdebug执行脚本(进入脚本所在文件夹下) k6 run --vus 100 --duration 10m --out csvresult.csv script.js 脚本解释&…...
小程序--vscode配置
要在vscode里开发微信小程序,需要安装以下两个插件: 安装后,即可使用vscode开发微信小程序。 注:若要实现鼠标悬浮提示,则需新建jsconfig.json文件,并进行配置,即可实现。 jsconfig.json内容如…...

linux僵尸进程
僵尸进程(Zombie Process)是指在一个进程终止时,其父进程尚未调用wait()或waitpid()函数来获取该进程的终止状态信息,导致进程的资源(如进程表中的记录)仍然保留在系统中的一种状态。 当一个进程结束时&am…...

【web | CTF】攻防世界 Web_php_unserialize
天命:这条反序列化题目也是比较特别,里面的漏洞知识点,在现在的php都被修复了 天命:而且这次反序列化的字符串数量跟其他题目不一样 <?php class Demo { // 初始化给变量内容,也就是当前文件,高亮显示…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...
