2.23C语言学习
P1480 A/B Problem
高精度数除以非高精度数
#include<bits/stdc++.h>
long long b[66660],c[66660],sum=0;
char a[66660];
int n;
int main(){scanf("%s",a);scanf("%d",&n);int len=strlen(a);for(int i=1;i<=len;i++){b[i]=a[i-1]-'0';}for(int i=1;i<=len;i++){c[i]=(b[i]+sum*10)/n;sum=(b[i]+sum*10)%n;}int flag=1;while(c[flag]==0&&flag<len)flag++;for(int i=flag;i<=len;i++){printf("%lld",c[i]);}return 0;
}P1109 学生分组
如果总人数在范围内,就不用输出-1
我们先用一个数组存下每个组的初始人数
那么,只有人数小于下限或大于上限才要调整 所有组多出来的人数和所有组缺的人数分别记成x、y x、y中更大的那个调到在范围内的组和范围外的组 所以,输出x、y中多的那个就可以了
#include<bits/stdc++.h>
using namespace std;
int main(){int n,a[60],sum=0;scanf("%d",&n);for(int i=1;i<=n;i++){scanf("%d",&a[i]);sum+=a[i];}int left,right,suma=0,sumb=0;scanf("%d %d",&left,&right);for(int i=1;i<=n;i++){if(a[i]<left){suma+=left-a[i];}else if(a[i]>right){sumb+=a[i]-right;}}if(sum<n*left||sum>n*right){printf("-1");return 0;}int ans=max(suma,sumb);printf("%d",ans);return 0;
}P2708 硬币翻转
当这一个硬币与下一个硬币不同时,这一个硬币连同它之前的硬币一起翻转
翻转至与下一个硬币相同的一面
直到将所有硬币翻转到同一面
但这里还有一个点要注意:
题目要求所有硬币正面朝上,也就是所有面都是'1'的情况,才算完成
我们就再把全部硬币翻转一次
那么这道题就好解决了
#include<bits/stdc++.h>
using namespace std;
int main(){string str;cin>>str;int cnt=0;for(int i=0;i<str.size()-1;i++){if(str[i]!=str[i+1])cnt++;}if(str[str.size()-1]=='0')cnt++;printf("%d",cnt);return 0;
}P1421 小玉买文具
水题,会写hello world都会写这个
#include<bits/stdc++.h>
using namespace std;
int main(){int x,y;cin>>x>>y;int sum=x*10+y;int nunm=sum/19;cout<<nunm;return 0;
}P1060 [NOIP2006 普及组] 开心的金明
01背包问题,对着模板来就行了
#include<bits/stdc++.h>
using namespace std;
int w[31],s[31],dp[30009];
int main(){int n,m;scanf("%d %d",&m,&n);for(int i=1;i<=n;i++){scanf("%d %d",&w[i],&s[i]);}for(int i=1;i<=n;i++){for(int j=m;j>=w[i];j--){dp[j]=max(dp[j],dp[j-w[i]]+w[i]*s[i]);}}cout<<dp[m];return 0;
}B3849 [GESP样题 三级] 进制转换
经典的精致转换,这里也是把我的板子献上
#include <bits/stdc++.h>
using namespace std;
int main()
{int a, b, cnt = 0;char arr[320] = { 0 };scanf("%d %d",&a,&b);while (a > 0) {int c = a % b;if (c > 9) {arr[cnt++] = (char)(c + 55);}else {arr[cnt++] = (char)(c + 48);}a /= b;}for (int j = cnt - 1; j >= 0; j--){cout << arr[j];}return 0;
}
相关文章:

2.23C语言学习
P1480 A/B Problem 高精度数除以非高精度数 #include<bits/stdc.h> long long b[66660],c[66660],sum0; char a[66660]; int n; int main(){scanf("%s",a);scanf("%d",&n);int lenstrlen(a);for(int i1;i<len;i){b[i]a[i-1]-0;}for(int i1;…...

origin/master master
这里实际上有三件事:origin master是两件事,origin/master一件事。共计三件事。 两个分支: master 是一个本地分支 origin/master是远程分支(它是名为“origin” 的远程分支的本地副本,名为“master”) 一个…...

【数据结构】时间复杂度与空间复杂度
目录 时间复杂度 空间复杂度 时间复杂度 算法的时间复杂度并不是指一个代码运行时间的快慢,因为在不同机器上运行的时间肯定不同,因此算法的时间复杂度指的是基本操作的执行次数,他是一个数学意义上的函数。这个函数并不是C语言中那种函数&…...

分别使用js与jquery写 单击按钮时出现内容 点击删除按钮不会再向下出现
HTML部分 <body><button id"btn">单击我</button><button id"delAll">删除所有事件</button><div id"test"></div> </bady>jQuery代码 <script type"text/JavaScript" src"…...
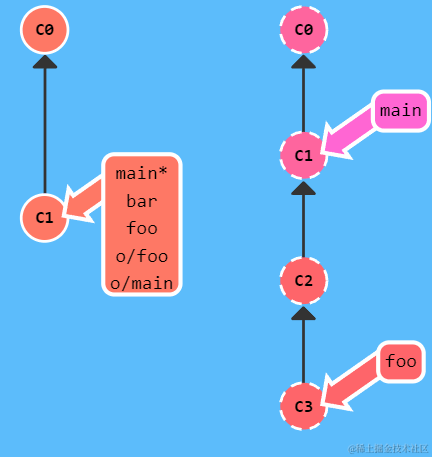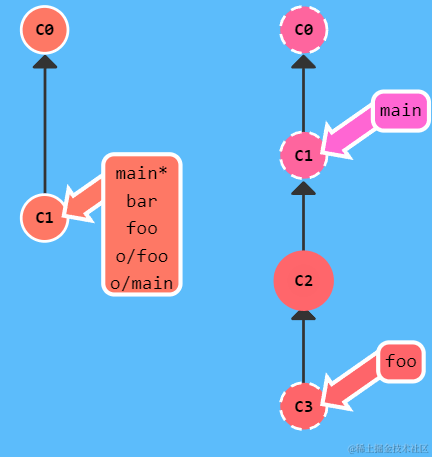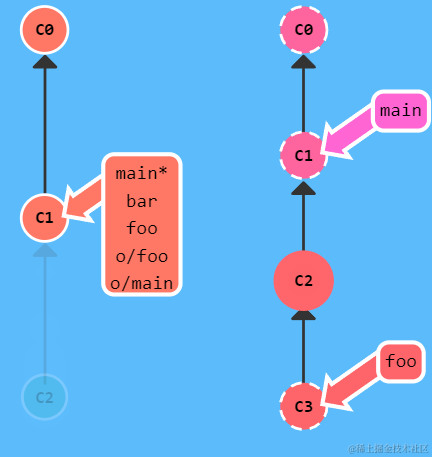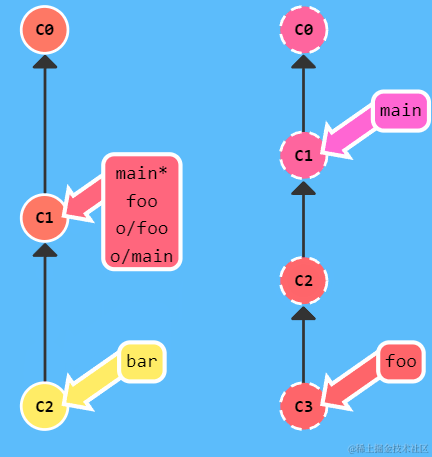
【Git】Git命令的学习与总结
本文实践于 Learn Git Branching 这个有趣的 Git 学习网站。在该网站,可以使用 show command 命令展示所有可用命令。你也可以直接访问网站的sandbox,自由发挥。 一、本地篇 基础篇 git commit git commit将暂存区(staging areaÿ…...

前端工程化面试题 | 18.精选前端工程化高频面试题
🤍 前端开发工程师、技术日更博主、已过CET6 🍨 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 🕠 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 🍚 蓝桥云课签约作者、上架课程《Vue.js 和 E…...

大公司的工程师是怎么废掉的...
大家好,我是砖一。 此文作者以嵌入式工程师为基本视角,细说了从初阶到高阶工程师的资质需求,并提示工程师职业道路上的陷阱。可供参考。 一,基础知识 一个嵌入式工程师,很多都是从51单片机或者STM32单片机开始&…...

将yolov8权重文件转为onnx格式并在c#中使用
yolo模型转ONNX 在yolov8中,我们将训练结果的.pt权重文件转换为onnx格式只需要使用ultralytics库中的YOLO类,使用pip安装ultralytics库,然后执行下面python代码 from ultralytics import YOLO# 加载YOLOv8模型 model YOLO("best.pt&q…...

在Spring Boot启动时禁止自动配置数据源相关的组件、@SpringBootApplication
一、SpringBootApplication(exclude {DataSourceAutoConfiguration.class})注解 在Spring Boot启动时禁止自动配置数据源相关的组件。 SpringBootApplication(exclude {DataSourceAutoConfiguration.class})注解的使用案例 这个注解通常应该写在微服务项目的主启动类上&…...

程序人生:不积跬步无以致千里
程序人生 癸卯年冬月,往渭南韩城,拜访司马迁祠。入门攀爬而上,至人有困乏之时,抬头现:高山仰止。归路下山,始现三官洞,遥想西汉时三官洞,出口处刻意再拜别:高山仰止。泪…...

通过二叉树例题深入理解递归问题
目录 引入: 例1:二叉树的前序遍历: 例2: N叉树的前序遍历: 例3:二叉树的最大深度: 例4:二叉树的最小深度 例5:N叉树的最大深度: 例6:左叶子…...

【Android 协程常见用法】
我们这里只讲解一下,协程在Android项目中常见用法,原理知识不在进行说明了。 依赖 lifecycleScope只能在Activity、Fragment中使用,会绑定Activity和Fragment的生命周期。依赖库: implementation androidx.lifecycle:lifecycle…...
python 进程笔记一 (概念+示例代码)
1. 进程的概念 进程是资源分配的最小单位,也是线程的容器,线程(python 线程 (概念示例代码))是CPU调度的基本单位,一个进程包括多个线程。 程序:例如xxx.py是一个程序 进程…...

各中间件数据库默认访问端口总结
说明 在生态丰富的开发环境下,我们常常需要接触很多中间件产品,中间件默认的连接端口以及可视化ui访问端口也时不时的需要用到,这里循序渐进做好登记,以备查阅! 中间件/数据库名称默认端口管理台端口默认账号密码rabbi…...

鲲鹏arm64架构下安装KubeSphere
鲲鹏arm64架构下安装KubeSphere 官方参考文档: https://kubesphere.io/zh/docs/quick-start/minimal-kubesphere-on-k8s/ 在Kubernetes基础上最小化安装 KubeSphere 前提条件 官方参考文档: https://kubesphere.io/zh/docs/installing-on-kubernetes/introduction/prerequi…...

python 函数-02-返回值注释格式
01 函数返回值 1)python中函数可以没有返回值,也可以有通过return的方式 – 【特殊性,区别于java c#等】 2)返回值可以是一个或者多个,多个时通过逗号隔开 – 【特殊性,区别于java c#等】 3)多…...
【前端素材】推荐优质后台管理系统Upcube平台模板(附源码)
一、需求分析 后台管理系统在多个层次上提供了丰富的功能和细致的管理手段,帮助管理员轻松管理和控制系统的各个方面。其灵活性和可扩展性使得后台管理系统成为各种网站、应用程序和系统不可或缺的管理工具。 当我们从多个层次来详细分析后台管理系统时࿰…...
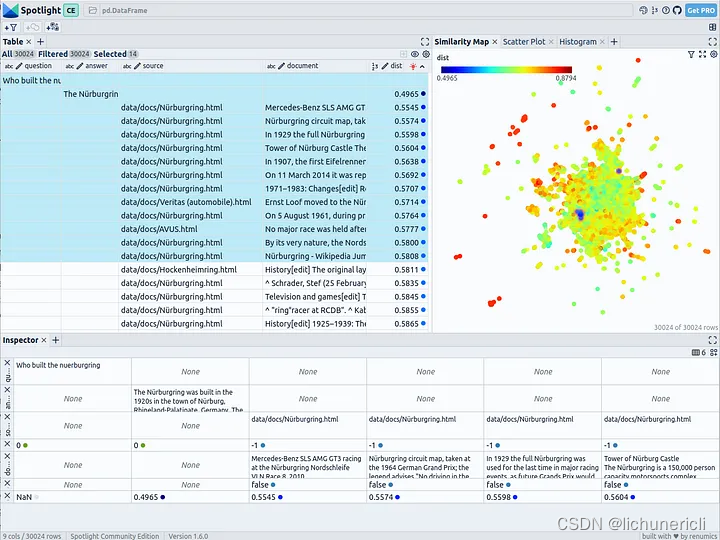
可视化 RAG 数据 — 用于检索增强生成的 EDA
原文地址:Visualize your RAG Data — EDA for Retrieval-Augmented Generation 2024 年 2 月 8 日 Github:https://github.com/Renumics/rag-demo/blob/main/notebooks/visualize_rag_tutorial.ipynb 为探索Spotlight中的数据,我们使用Pa…...

数学建模论文、代码百度网盘链接
1.[2018中国大数据年终总决赛冠军] 金融市场板块划分与轮动规律挖掘与可视化问题 2.[2019第九届MathorCup数模二等奖] 数据驱动的城市轨道交通网络优化策略 3.[2019电工杯一等奖] 露天停车场停车位的优化设计 4.[2019数学中国网络数模一等奖] 基于机器学习的保险业数字化变革…...

mysql 迁移-data目录拷贝方式
背景:从服务器进水坏掉,50多G的数据库要重新做主从,但以导入导出的方式太慢,简直是灾难性的,一夜都没好,只好想到了拷贝mysql数据文件的方式 拷贝的数据文件的前提 1.数据库版本必需一致(可以…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
