Leetcoder Day21| 回溯理论基础+组合
语言:Java/Go
回溯理论基础
回溯函数也就是递归函数;
所有回溯法的问题都可以抽象为树形结构;
回溯法解决的都是在集合中递归查找子集,集合的大小就构成了树的宽度,递归的深度,都构成的树的深度。
适用的题目类型:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 棋盘问题:N皇后,解数独等等
组合无序,排列有序
回溯法解题模板
- 回溯函数返回值及参数:回溯算法中函数返回值一般为void。需要什么参数,就填什么参数
void backtracking(参数)
- 回溯函数终止条件:一般搜到叶子节点了,也就找到了满足条件的一条答案,把这个答案存放起来,并结束本层递归。
if (终止条件) {存放结果;return; }
- 回溯搜索的遍历过程
 上图中,集合大小和孩子的数量是相等的,for循环就是遍历集合区间,可以理解一个节点有多少个孩子,这个for循环就执行多少次。for循环可以理解是横向遍历,backtracking(递归)就是纵向遍历,这样就把这棵树全遍历完了,一般来说,搜索叶子节点就是找的其中一个结果了
上图中,集合大小和孩子的数量是相等的,for循环就是遍历集合区间,可以理解一个节点有多少个孩子,这个for循环就执行多少次。for循环可以理解是横向遍历,backtracking(递归)就是纵向遍历,这样就把这棵树全遍历完了,一般来说,搜索叶子节点就是找的其中一个结果了 for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果 }
因此,回溯算法模板框架如下:
void backtracking(参数) {if (终止条件) {存放结果;return;}for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {处理节点;backtracking(路径,选择列表); // 递归回溯,撤销处理结果}
}
组合
给定两个整数
n和k,返回范围[1, n]中所有可能的k个数的组合。你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2 输出: [[2,4],[3,4],[2,3],[1,2],[1,3],[1,4], ]
组合的题目如果单纯的采用for循环暴力求解,k越大,for嵌套层数就越多很崩溃。因此采用回溯算法,当然,回溯算法本身也是暴力求解,但胜在书写方便。其原理是用递归来解决嵌套层数的问题。每一次的递归中嵌套一个for循环,就可以用于解决多层嵌套循环的问题了。
因此把上面的组合问题抽象为如下树形结构:

这棵树一开始集合是 1,2,3,4, 从左向右取数,取过的数,不再重复取。第一次取1,集合变为2,3,4 ,因为k为2,我们只需要再取一个数就可以了,分别取2,3,4,得到集合[1,2] [1,3] [1,4],以此类推。n相当于树的宽度,k相当于树的深度,图中每次搜索到了叶子节点,我们就找到了一个结果。
因此首先确定回溯三部曲:
- 递归函数的返回值以及参数:首先要定义两个全局变量,一个用来存放符合条件单一结果,一个用来存放符合条件结果的集合;函数里有n和k两个int型的参数;还需要一个参数,为int型变量startIdx,这个参数用来记录本层递归的中,集合从哪里开始遍历。startIdx 是防止出现重复的组合。在集合[1,2,3,4]取1之后,下一层递归,就要在[2,3,4]中取数了,那么下一层递归如何知道从[2,3,4]中取数呢,靠的就是startIdx。用startIdx来记录下一层递归,搜索的起始位置。
- 回溯函数终止条件:path这个数组的大小如果达到k,说明我们找到了一个子集大小为k的组合了,在图中path存的就是根节点到叶子节点的路径。此时用result二维数组,把path保存起来,并终止本层递归。
- 单层搜索的过程:for循环每次从startIndex开始遍历,然后用path保存取到的节点i;backtracking(递归函数)通过不断调用自己一直往深处遍历,总会遇到叶子节点,遇到了叶子节点就要返回。然后进行回溯,撤销本次处理的结果,便于进行下一次递归。
剪枝优化
如果n = 4,k = 4的话,那么第一层for循环的时候,从元素2开始的遍历都没有意义了。 在第二层for循环,从元素3开始的遍历都没有意义了。
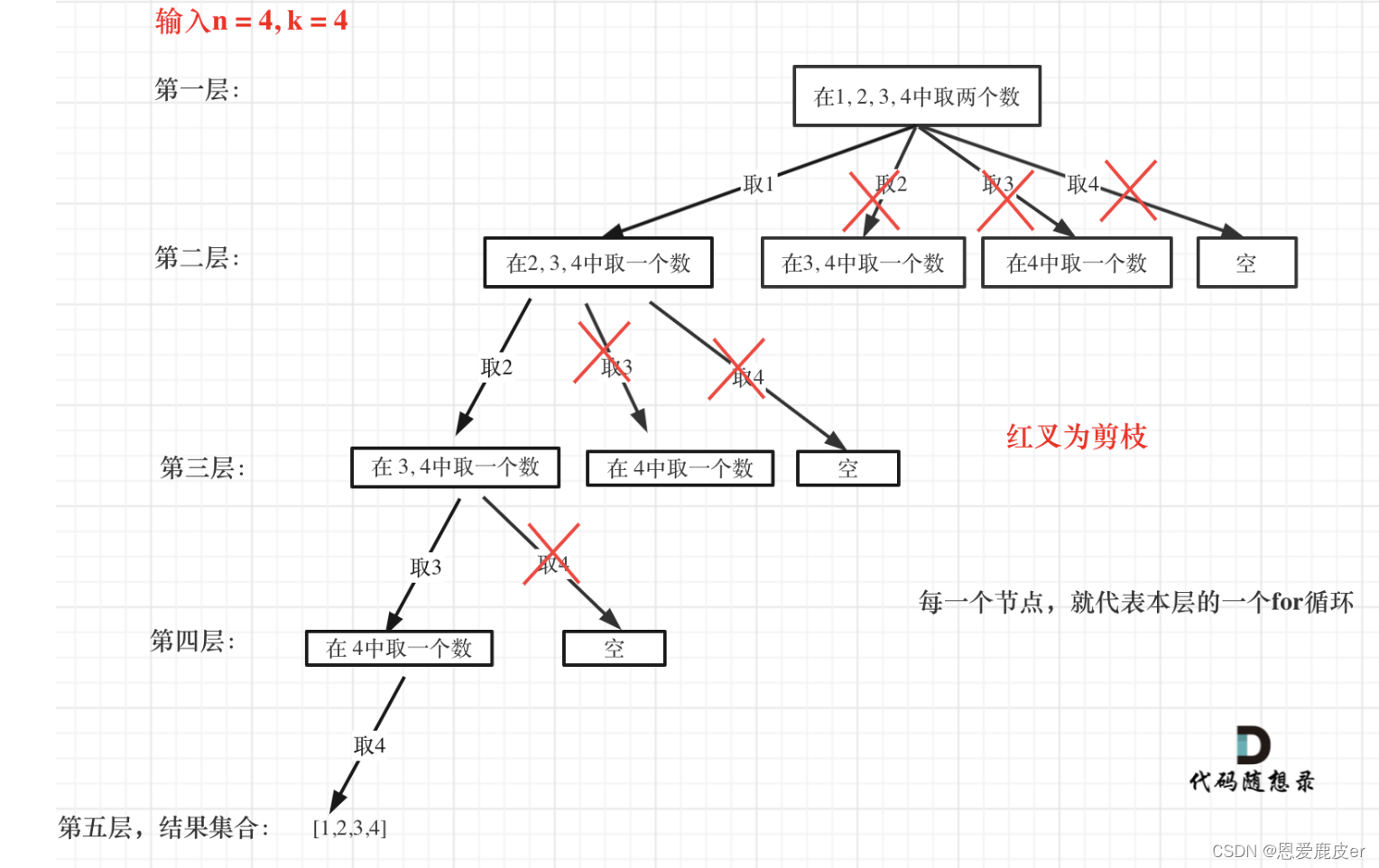
图中每一个节点(图中为矩形),就代表本层的一个for循环,那么每一层的for循环从第二个数开始遍历的话,都没有意义,都是无效遍历。
所以,可以剪枝的地方就在递归中每一层的for循环所选择的起始位置。
如果for循环选择的起始位置之后的元素个数 已经不足 我们需要的元素个数了,那么就没有必要搜索了。
看一下优化过程如下:
-
已经选择的元素个数:path.size();
-
还需要的元素个数为: k - path.size();
-
在集合n中至多要从该起始位置 : n - (k - path.size()) + 1,开始遍历
为什么有个+1呢,因为包括起始位置,我们要是一个左闭的集合。
举个例子,n = 4,k = 3, 目前已经选取的元素为0(path.size为0),n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。
从2开始搜索都是合理的,可以是组合[2, 3, 4]。
所以优化之后的for循环是:
for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) // i为本次搜索的起始位置
class Solution {List<List<Integer>> res = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();public void backTracking(int n, int k, int startIdx){//startIdx标志从哪开始循环if(path.size()==k){res.add(new ArrayList<>(path));return;}for(int i=startIdx;i<=n-(k-path.size())+1;i++){//剪枝path.add(i);backTracking(n,k,i+1); //递归path.removeLast();}} public List<List<Integer>> combine(int n, int k) {backTracking(n,k,1);return res;}
}今日心得
开启回溯章节,在这一章要多熟悉回溯三部曲,以及捋清楚回溯的内在逻辑。并且注意数组、列表和树的操作。
相关文章:

Leetcoder Day21| 回溯理论基础+组合
语言:Java/Go 回溯理论基础 回溯函数也就是递归函数; 所有回溯法的问题都可以抽象为树形结构; 回溯法解决的都是在集合中递归查找子集,集合的大小就构成了树的宽度,递归的深度,都构成的树的深度。 适用的题…...
备战蓝桥杯Day17 - 链表
链表 基本概念 链表是由一系列节点组成的元素集合。 每个节点包含两部分:数据域 item 、指向下一个节点的指针 next 通过节点之间的相互链接,形成一个链表 1. 链表的初始化 # 手动建立链表 # 链表的初始化 class Node(object):def __init__(self, …...
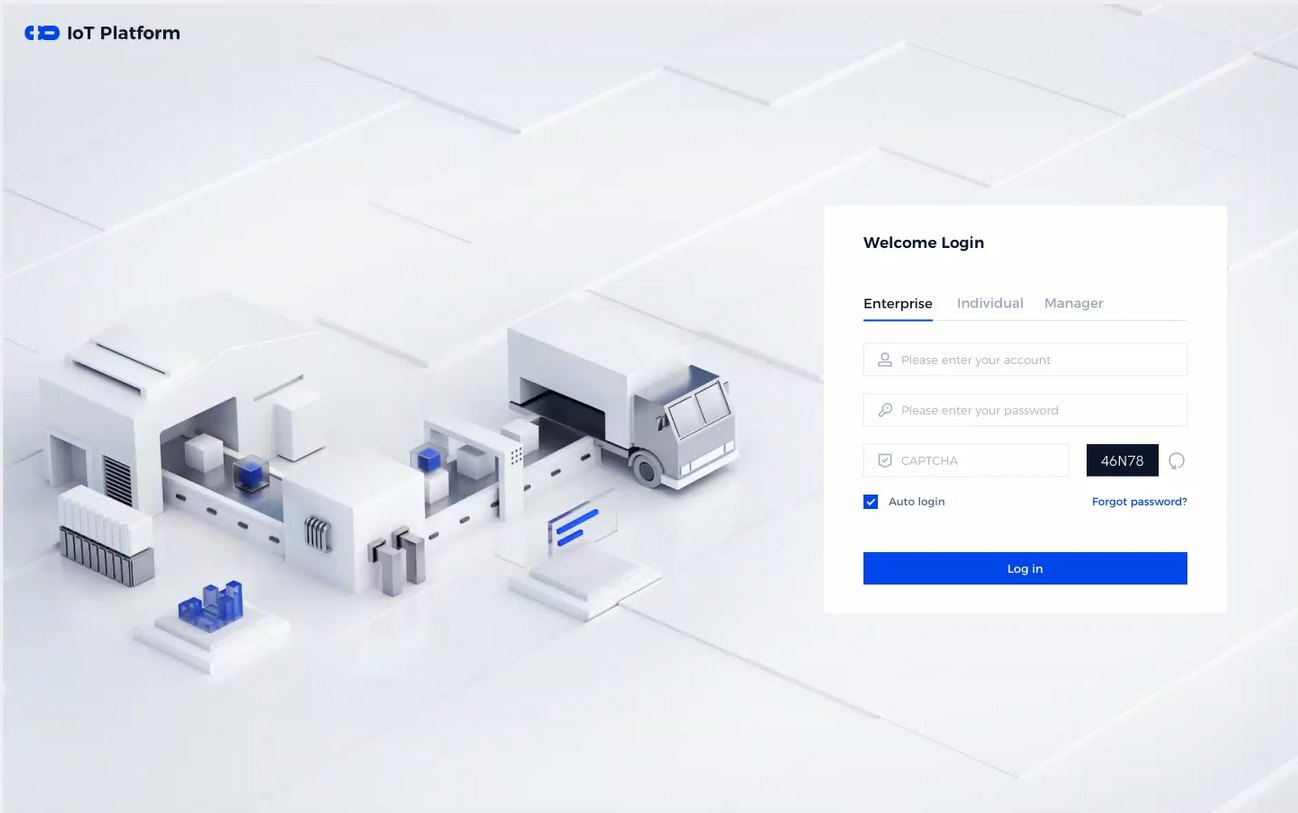
登录页设计新选择:毛玻璃和新拟态风格,非2.5D和插画风
登录页给潜在用户传递了产品的品牌调性,是非常重要的一类页面,之前2.5D和插画风格的登录页流行一时,不过这阵风好像过去了,新的风格开始涌现了。 一、越来越流行的毛玻璃设计风格 毛玻璃风格是指将背景模糊处理,使得…...

14:00面试,14:05就出来了,问的问题有点变态。。。
下午两点,我准时走进了面试的会议室,心中既有期待也有紧张。然而,仅仅五分钟后,我便走出了会议室,心中充满了困惑和挫败感。面试官的问题确实出乎我的预料,它们既深入又具体,让我有些措手不及。…...

关于纯前端想要变成全栈编写接口的学习推荐
推荐学习uniappuniclouduniadmin 学习成本低,不到一个月就能开发出自己的接口,上传到服务空间,并且能够实现后端的功能,能够调用接口 当然这里使用的不是mysql数据库,而是unicloud推荐的存储方式 操作起来也很方便...

Rust升级慢,使用国内镜像进行加速
背景 rustup 是 Rust 官方的跨平台 Rust 安装工具,国内用户使用rustup update的时候,网速非常慢,可以使用国内的阿里云镜像源来进行加速 0x01 配置方法 1. Linux与Mac OS用户配置环境变量 修改~/.bash_profile文件添加如下内容࿱…...

Base64 编码 lua
Base64 编码 -- Base64 字符表 local base64_chars { A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W, X, Y, Z, a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,…...
41.仿简道云公式函数实战-数学函数-SUMIF
1. SUMIF函数 SUMIF 函数可用于计算子表单中满足某一条件的数字相加并返回和。 2. 函数用法 SUMIF(range, criteria, [sum_range]) 其中各参数的含义及使用方法如下: range:必需;根据 criteria 的条件规则进行检测的判断字段。支持的字段…...

挑战30天学完Python:Day22 爬虫
🎉 本系列为Python基础学习,原稿来源于 30-Days-Of-Python 英文项目,大奇主要是对其本地化翻译、逐条验证和补充,想通过30天完成正儿八经的系统化实践。此系列适合零基础同学,或仅了解Python一点知识,但又没…...

AI:138-开发一种能够自动化生成艺术品描述的人工智能系统
🚀点击这里跳转到本专栏,可查阅专栏顶置最新的指南宝典~ 🎉🎊🎉 你的技术旅程将在这里启航! 从基础到实践,深入学习。无论你是初学者还是经验丰富的老手,对于本专栏案例和项目实践都有参考学习意义。 ✨✨✨ 每一个案例都附带关键代码,详细讲解供大家学习,希望…...
智慧城市建设的新里程碑:公共服务电子支付大屏
随着科技的飞速发展,我们的生活正在经历前所未有的变革。电子支付的出现,无疑是这场变革中的一大亮点,它不仅改变了我们日常的支付方式,更成为智慧城市建设的重要一环,为公众提供了更加便捷、高效的服务体验。 在以前&…...

Netty之Decoder详解与实战
在这篇博客文章中,我们将深入探讨Netty框架中的一个核心组件——Decoder,并通过示例解释其工作原理及如何在Netty应用程序中使用它来处理网络通信中的数据解码。 1. 什么是Decoder? 在Netty中,Decoder是一种特殊类型的ChannelHa…...
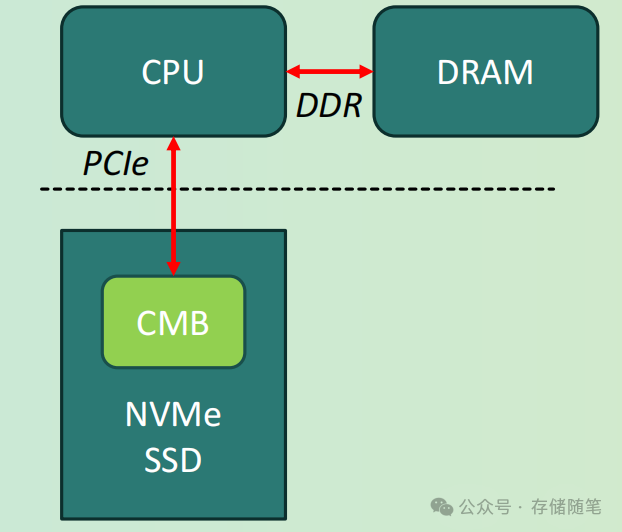
PCIe P2P DMA全景解读
温馨提醒:本文主要分为5个部分,总计4842字,需要时间较长,建议先收藏! P2P DMA简介 P2P DMA软硬件支持 CXL P2P DMA原理差异 P2P DMA应用场景 P2P DMA技术挑战 一、P2P DMA简介 P2P DMA(Peer-to-Peer…...

【Git】window下大小写不敏感问题处理
在Windows环境下,Git因为文件名的大小写敏感性而导致了一些问题。 首先,Windows文件系统是不区分大小写的,这意味着在Windows中创建的两个文件名只有大小写不同,但字母顺序和字符完全相同的文件会被视为相同的文件。然而…...

【JS】【Vue3】【React】获取滚轮位置的方法:JavaScript、Vue 3和React示例
目录 使用JavaScript原生方法在Vue 3中获取滚轮位置在React中获取滚轮位置 随着Web应用程序的发展,滚轮位置的获取变得越来越重要,可以用于实现页面的滚动效果、导航条的隐藏和显示等功能。本文将探讨在JavaScript、Vue 3和React中获取滚轮位置的不同方法…...
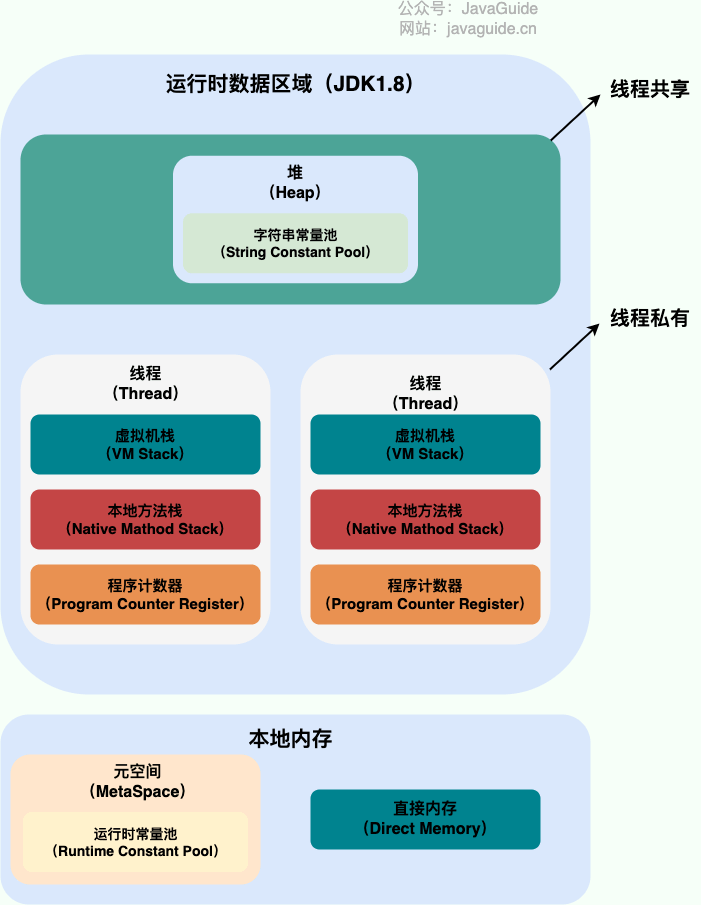
什么是线程和进程?
什么是线程和进程? 文章目录 什么是线程和进程?何为进程?何为线程? Java 线程和操作系统的线程有啥区别?请简要描述线程与进程的关系,区别及优缺点?图解进程和线程的关系程序计数器为什么是私有的?虚拟机栈和本地方法栈为什么是私有的?一句话简单了…...
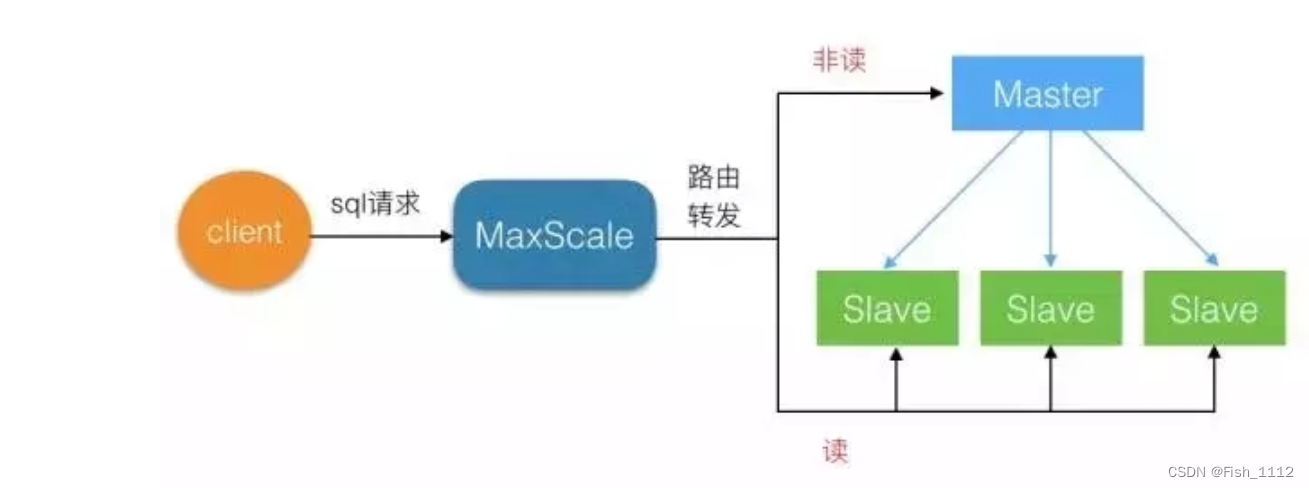
MaxScale实现mysql8读写分离
MaxScale 实验环境 中间件192.168.150.24MaxScale 22.08.4主服务器192.168.150.21mysql 8.0.30从服务器192.168.150.22mysql 8.0.30从服务器192.168.150.23mysql 8.0.30 读写分离基于主从同步 1.先实现数据库主从同步 基于gtid的主从同步配置 主库配置 # tail -3 /etc/my.…...
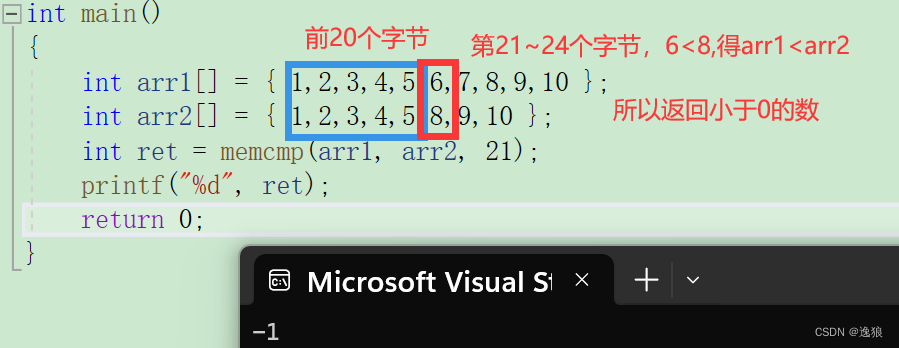
【c语言】内存函数
欢迎关注个人主页:逸狼 创造不易,可以点点赞吗~ 如有错误,欢迎指出~ 目录 memcpy函数的使用和模拟实现 memcpy函数的使用 memcpy函数的模拟实现 memmove的使用和模拟实现 memmove的使用 memmove的模拟实现 memset函数的使用 memcmp函数…...

规则引擎项目
https://github.com/expr-lang/expr https://github.com/gorules/zen...

Docker Image(镜像)
“脚印会旧而梦还在走” Docker 镜像介绍 (1) 如何理解镜像? 🎯 docker image本质就是一个 read-only(只读)文件,这个文件包含了文件系统、源码、库文件、依赖文件、工具等一些运行 application 所必须的文件。 🎯 我们也可以…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...
