【力扣】整数反转,判断是否溢出的数学解法
整数反转原题地址
方法一:数学
反转整数
如何反转一个整数呢?考虑整数操作的3个技巧:
- xmod10 可以取出 x 的最低位,如 x=123 , xmod10=3 。
- x/=10 可以去掉 x 的最低位,如 x=123 , x/=10 , x=12 。
- x=x*10+y 可以在 x 后面续上 y ,其中 y 是一位数,如 x=123 , y=4 , x=x*10+y , x=1234 。
假设要反转的整数为 x ,反转后的整数存储在变量 rev 中, rev 一开始初始化为 0 ,那么反复执行以下操作:
- digit=xmod10 ,取出 x 的最低位数。
- x/=10 ,去掉 x 的最低位数。
- rev=rev*10+digit ,在 rev 后面续上 digit 。
直到 x 为 0 为止,此时 rev 存储的数据符合题目要求。
判断溢出
问题在于,如何判断插入后的数据是否超出 [INT_MIN,INT_MAX] 的范围,导致溢出?
我们来探索不等式 成立的充分必要条件。
先看右半边,即 。
对于任意整数 i ,我们有 ,如对于 123 , 123/10=12 , 123mod10=3 , 123=12*10+3 。
不等式化为: ,带入
,
,
,
移项化简得: ,记
,
- 当 rev=m 时,如果还要推入数字,那么 digit≤2 ,因为 INT_MAX 的最高位为 2 ,此时不等式左边等于 0 ,右边为正数,不等式恒成立。
- 当 rev>m 时,不等式左边至少是 10 ,右边至多是 7 ,不等式恒不成立。
- 当 rev<m 时,不等式左边至多是 -10 ,右边至少是 7-9=-2 ,不等式恒成立。
所以原不等式右半边成立的充分必要条件是 ,即
。同理左半边成立的充分必要条件是
。
原不等式成立的充分必要条件是 。
// 方法一:数学
class Solution
{
public:int reverse(int x){int rev = 0;while (x){if (rev < INT_MIN / 10 || rev > INT_MAX / 10){return 0;}// rev 后面续上 x 的最低位rev = rev * 10 + x % 10;// 去掉 x 的最低位x /= 10;}return rev;}
};相关文章:
【力扣】整数反转,判断是否溢出的数学解法
整数反转原题地址 方法一:数学 反转整数 如何反转一个整数呢?考虑整数操作的3个技巧: xmod10 可以取出 x 的最低位,如 x123 , xmod103 。x/10 可以去掉 x 的最低位,如 x123 , x/10 …...
Jmeter之内置函数__property和__P的区别
1. __property函数 作用 读取 Jmeter 属性 语法格式 ${__property(key,var,default)} 参数讲解 小栗子 ${__property(key)} 读取 key 属性如果找不到 key 属性,则返回 key(属性名) ${__property(key,,default)} 读取 key 属性如果找不到 k…...
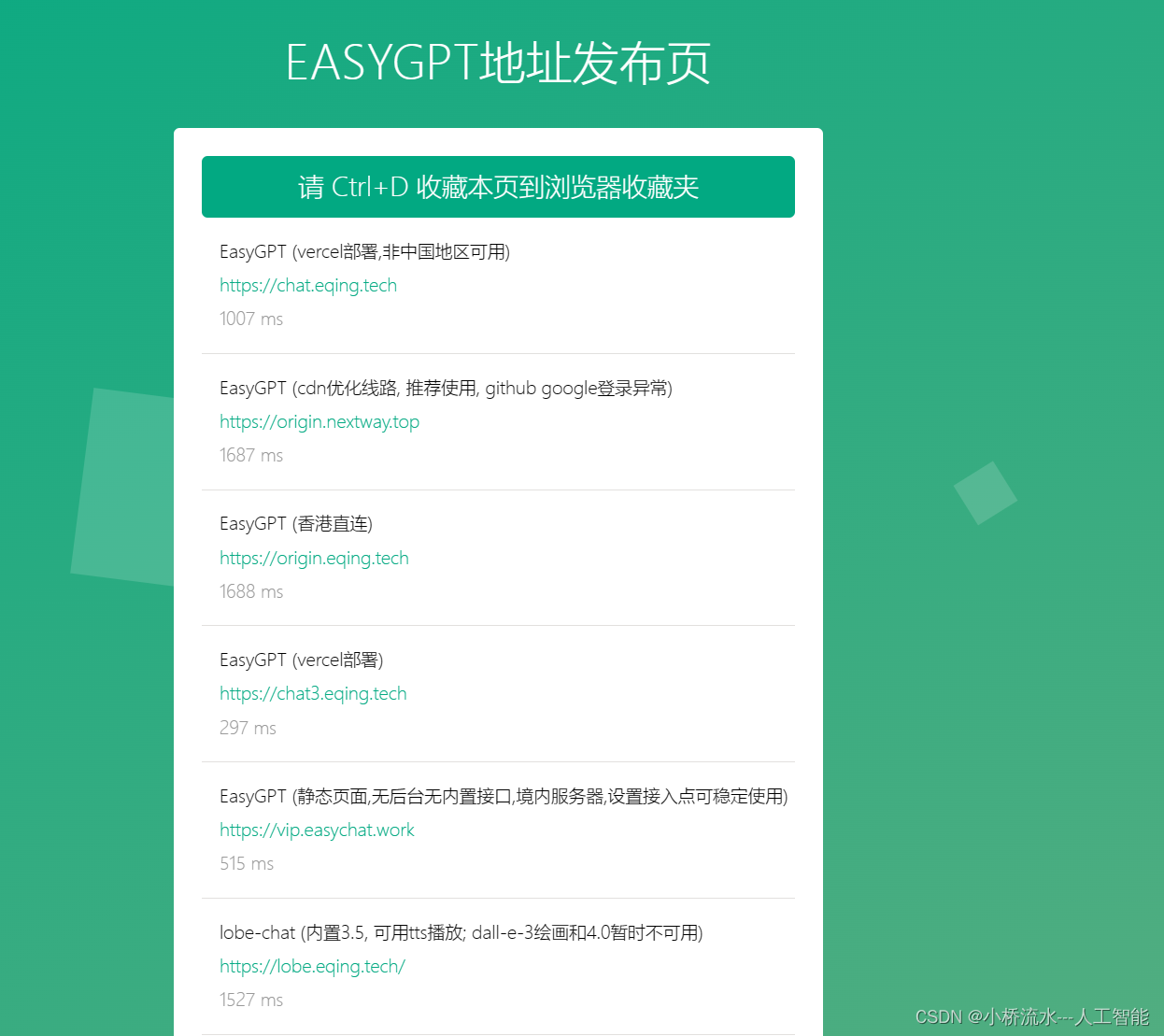
GPT润色指令
1. GPT润色指令 Below is a paragraph from an academic paper. Polish the writing to meet the academic style,improve the spelling, grammar, clarity, concision and overall readability. When necessary, rewrite the whole sentence. Paragraph :你的句子…...

Ubuntu中matplotlib显示中文的方法
其实有很多朋友已经总结得很好了:Ubuntu下让matplotlib显示中文字体_ubuntu matplot 使用汉字-CSDN博客 这里我就是简单补充一下: 按照上面这篇博客,下载:GitHub - tracyone/program_font: fonts for programmer 然后运行&#…...
-StringBuilder-StringJoiner-打乱字符串)
String类-equals和==的区别-遍历-SubString()-StringBuilder-StringJoiner-打乱字符串
概述 String 类代表字符串,Java 程序中的所有字符串文字(例如“abc”)都被实现为此类的实例。也就是说,Java 程序中所有的双引号字符串,都是 String 类的对象。String 类在 java.lang 包下,所以使用的时候…...
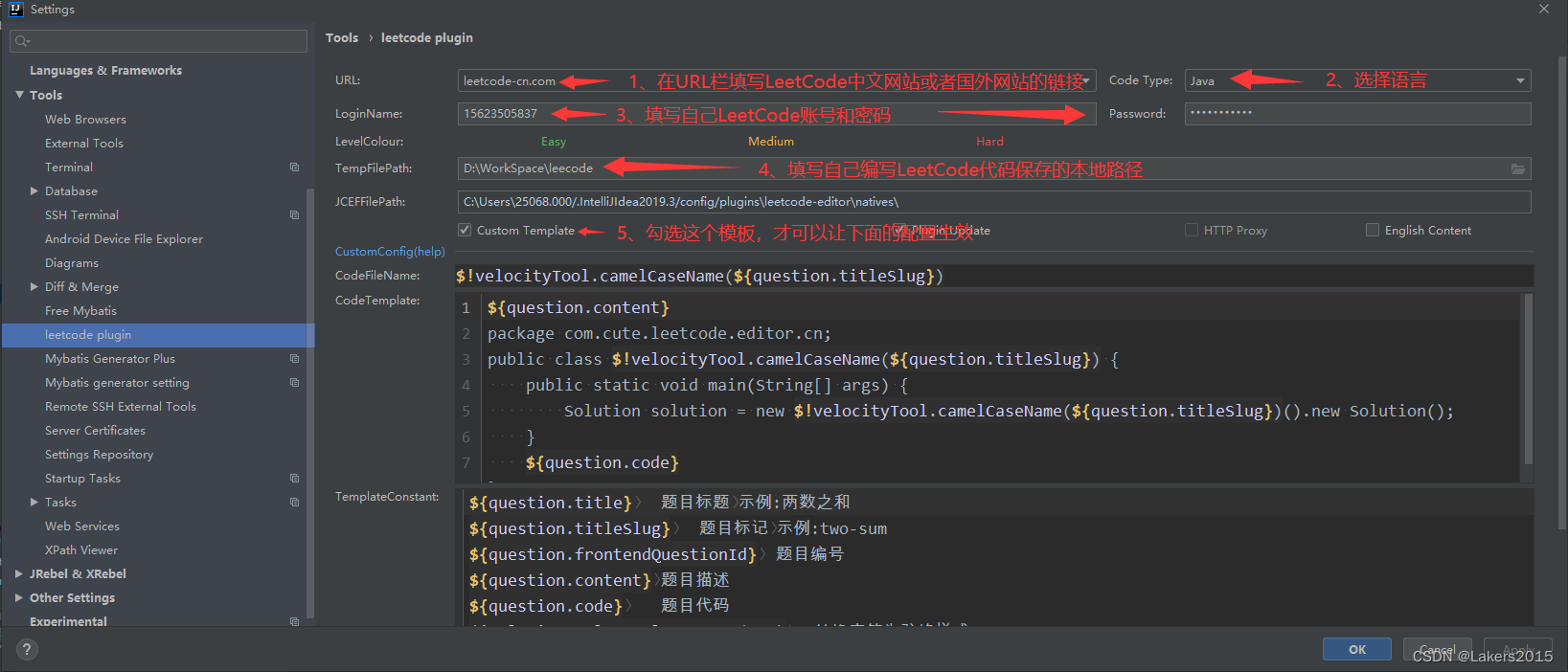
IDEA的LeetCode插件的设置
一、下载插件 选择点击File->Setting->Plugins:搜索LeetCode 二、打开这个插件 选择View —>Tool Windows—>leetcode 三、登陆自己的账号 关于下面几个参数的定义,官方给的是: Custom code template: 开启使用自定义模板&…...
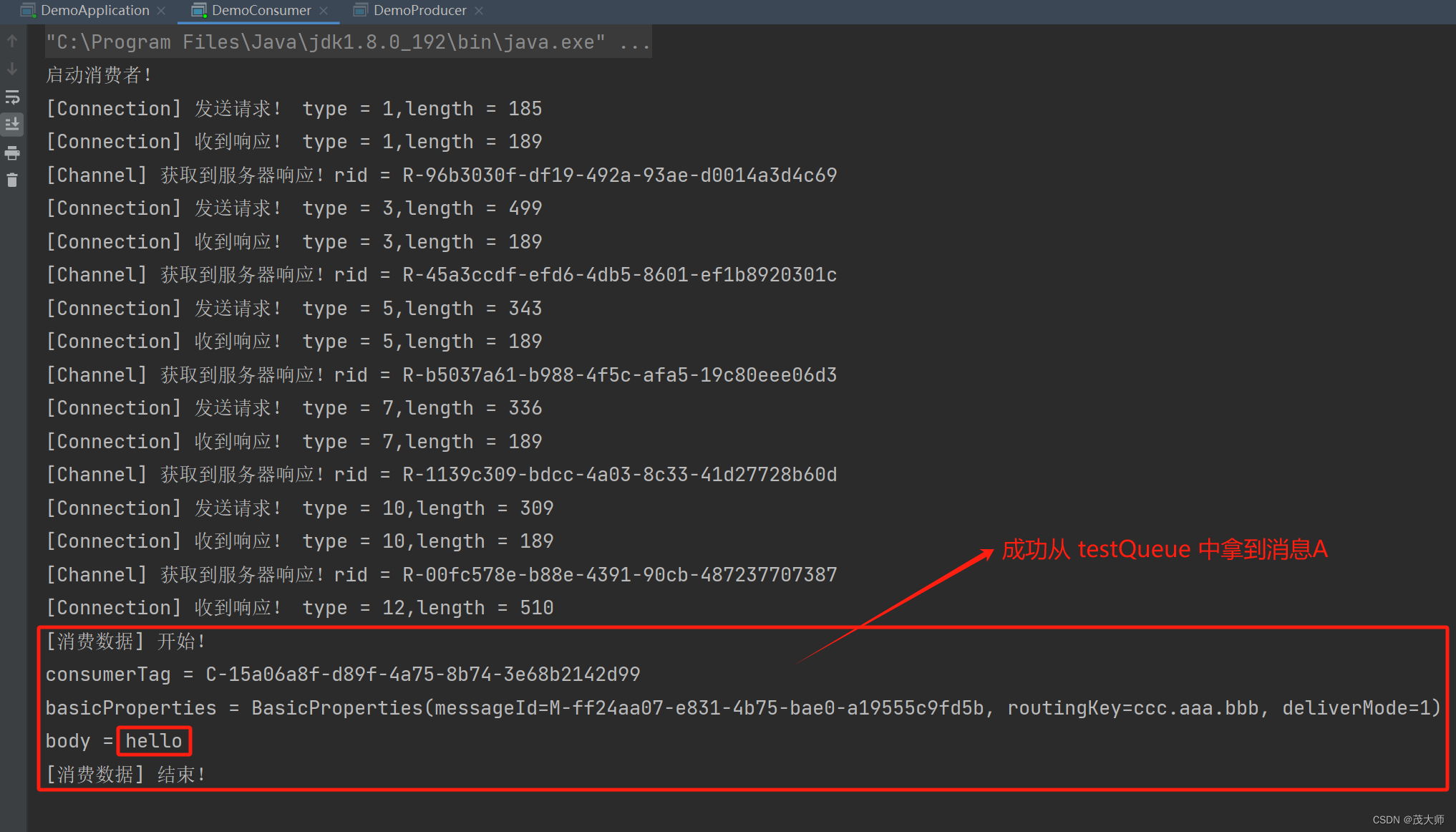
2024.2.29 模拟实现 RabbitMQ —— 项目展示
目录 项目介绍 核心功能 核心技术 演示直接交换机 演示扇出交换机 演示主题交换机 项目介绍 此处我们模拟 RabbitMQ 实现了一个消息队列服务器 核心功能 提供了 虚拟主机、交换机、队列、绑定、消息 概念的管理九大核心 API 创建队列、销毁队列、创建交换机、销毁交换机、…...

React htmlfor
注意,在添加属性时, class 属性需要写成 className ,for 属性需要写成 htmlFor ,这是因为 class 和 for 是 JavaScript 的保留字。 在React中,当我们需要为一个表单元素设置标签时,可以使用htmlFor属性。它…...

现代化数据架构升级:毫末智行自动驾驶如何应对年增20PB的数据规模挑战?
毫末智行是一家致力于自动驾驶的人工智能技术公司,其前身是长城汽车智能驾驶前瞻分部,以零事故、零拥堵、自由出行和高效物流为目标,助力合作伙伴重塑和全面升级整个社会的出行及物流方式。 在自动驾驶领域中,是什么原因让毫末智行…...

理解Stable Diffusion、LoRA、Dreambooth、Hypernetworks、Textual Inversion、Checkpoint
前言 在深度学习和人工智能的领域中,模型生成和调整技术的快速发展为创造性内容的自动化提供了新的可能性。本文将介绍四种重要的模型技术——Stable Diffusion、LoRA、Dreambooth、和Hypernetworks——它们在生成艺术、个性化模型调整和网络结构设计方面各自的特点…...
spring boot3登录开发-2(1图形验证码接口实现)
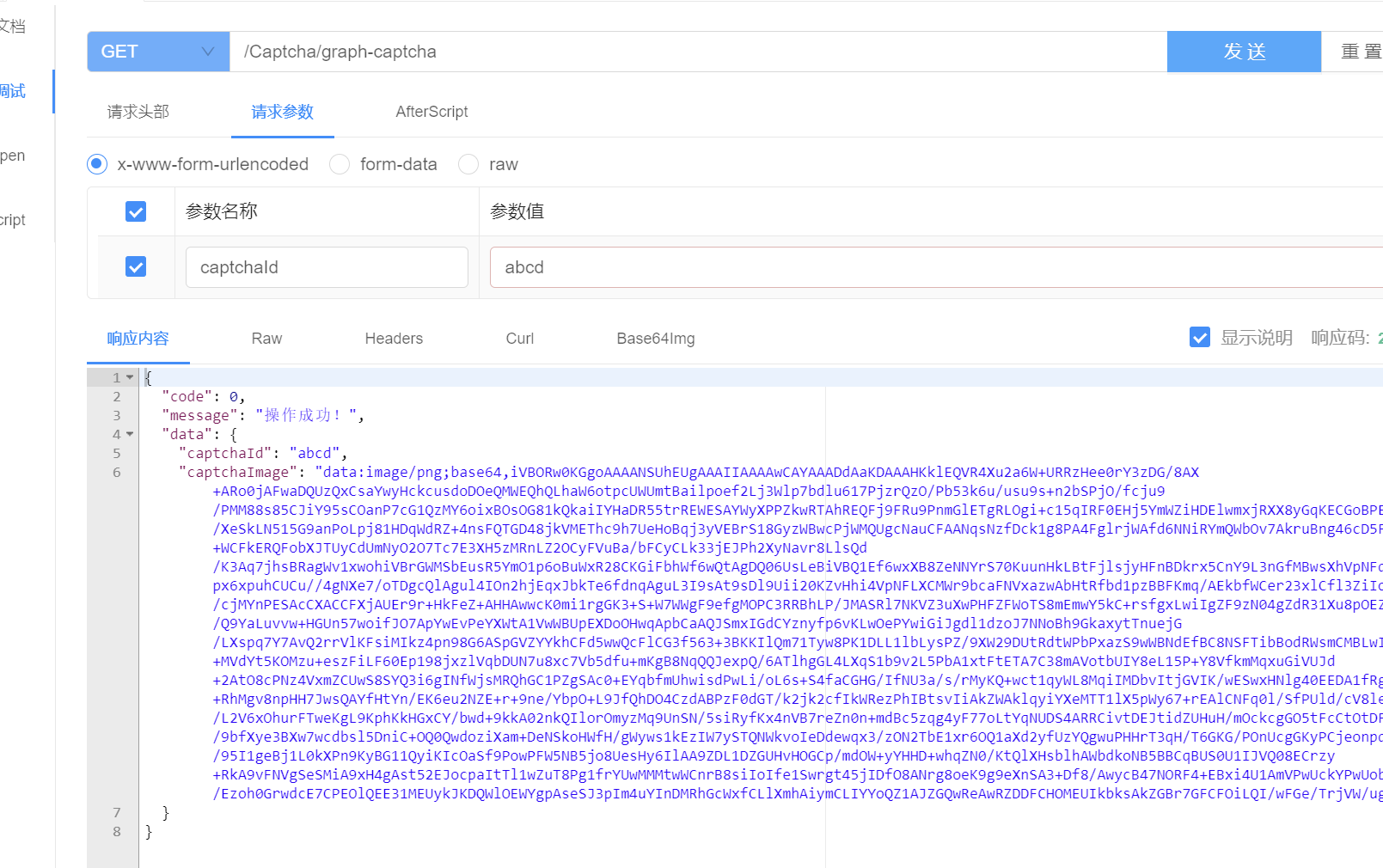
⛰️个人主页: 蒾酒 🔥系列专栏:《spring boot实战》 🌊山高路远,行路漫漫,终有归途。 目录 前置条件 内容简介 图形验证码接口实现 导入糊涂工具依赖 接口分析 编写验证码接口 测试验证码接口 前置条件 …...

网络编程中的问题总结
1、服务端重启后bind失败,因为TCP 套接字状态 TIME_WAIT 引起,该状态在套接字关闭后约保留 2 到 4 分钟。在 TIME_WAIT 状态退出之后,套接字被删除,该地址才能被重新绑定而不出问题。可以通过setsockopt()设置Socket描述符的选项S…...
数据结构-关键路径
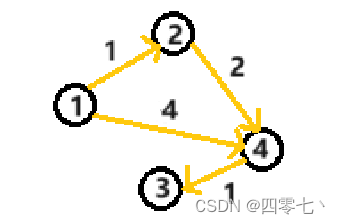
介绍 在AOV网的基础上,如果用对应边来表示活动持续时间,这种有向图被称为AOE网在AOE网中,入度为0的为源点,出度为0的为汇点,整张网看做是一件事情完成的过程,那么这两个点就是事情的开始和结束。每个活动持…...

进程间通信学习笔记(共享内存)
内存映射概念: 共享内存可以通过mmap()映射普通文件使一个磁盘文件与内存中的一个缓冲区相映射,进程可以像访问普通文件一样对文件进行访问,不必再强调read,write。 mmap的优点: 实现了用户空间和内核空间的高效交互方式 mmap的…...

ChatGPT学习第三周
📖 学习目标 ChatGPT在各行各业的应用 探索ChatGPT在不同领域(如教育、客户服务等)的实际应用案例。 ChatGPT的局限性和挑战 讨论ChatGPT面临的挑战,包括偏见、误解及其限制。 ✍️ 学习活动 学习资料 《人工智能通用大模型(…...

R语言混合效应(多水平/层次/嵌套)模型及贝叶斯实现技术应用
回归分析是科学研究中十分重要的数据分析工具。随着现代统计技术发展,回归分析方法得到了极大改进。混合效应模型(Mixed effect model),即多水平模(Multilevel model)/分层模型(Hierarchical Model)/嵌套模…...
[C++]使用C++部署yolov9的tensorrt模型进行目标检测
部署YOLOv9的TensorRT模型进行目标检测是一个涉及多个步骤的过程,主要包括准备环境、模型转换、编写代码和模型推理。 首先,确保你的开发环境已安装了NVIDIA的TensorRT。TensorRT是一个用于高效推理的SDK,它能对TensorFlow、PyTorch等框架训…...

eureka注册中心做了哪些事情/原理?
1.服务注册: 将eureka client发送过来的元数据存储到注册表中 2.服务续约: eureka client默认会每30秒向eureka server发送一次心跳来进行服务续约,通过这一行动来表示自己没有出现故障; 3.服务…...

c语言经典测试题4
1.题1 #include <stdio.h>//没有break的话,输入什么都会往下一直执行下去,而且default在最后就会全都执行 int main() {char c;int v0 0, v1 0, v2 0;do{switch (c getchar())// 输入ADescriptor{casea:caseA:casee:caseE:casei:caseI:caseo:…...
设计模式(五)-观察者模式
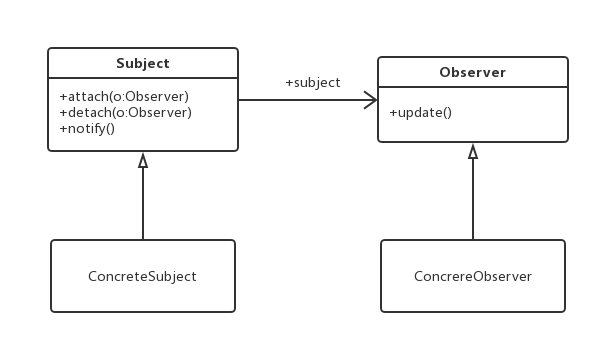
前言 实际业务开发过程中,业务逻辑可能非常复杂,核心业务 N 个子业务。如果都放到一块儿去做,代码可能会很长,耦合度不断攀升,维护起来也麻烦,甚至头疼。还有一些业务场景不需要在一次请求中同步完成&…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...
