R语言混合效应(多水平/层次/嵌套)模型及贝叶斯实现技术应用
回归分析是科学研究中十分重要的数据分析工具。随着现代统计技术发展,回归分析方法得到了极大改进。混合效应模型(Mixed effect model),即多水平模(Multilevel model)/分层模型(Hierarchical Model)/嵌套模型(Nested Model),无疑是现代回归分析中应用最为广泛的统计模型,代表了现代回归分析主流发展方向。混合效应模型形式灵活可以应对现代科学研究中各种数据情况,与传统回归模型相比具有更为强大数据分析能力,且结果更为可信。本课程将分为复杂数据的回归及混合效应模型概述及数据探索;回归与混合效应模型,包括一般线性回归(lm)、广义线性回归(glm);线性混合效应模型(lmm)及广义线性混合效应模型(glmm);贝叶斯(brms)回归与混合效应模型;相关数据回归与混合效应模型及贝叶斯实现,包括嵌套数据、时间自相关数据,空间自相数据及系统发育数据分析;非线性数据回归分析及贝叶斯实现,包括广义可加(混合)模型和非线性(混合)模型等。
张博士:来自中国科学院及重点高校资深专家,长期从事R语言模型、群落生态学、保护生物学、景观生态学和生态模型方面的研究和教学工作,以发表了多篇论文,拥有丰富的科研及实践经验。
复杂数据的回归及混合效应模型概述及数据探索
1复杂数据回归模型的选择策略
1)科学研究中数据及其复杂性
2)回归分析历史、理论基础
3)回归分析基本假设和常见问题
4)复杂数据回归模型选择策略

2如何通过数据探索避免常见统计问题
- 数据缺失(missing value)
- 零值(zero trouble)
- 奇异值/离群值(outliers)
- 异质性(heterogeneity)
- 数据分布正态性(normality)
- 响应变量与预测变量间关系(relationships)
- 交互作用项(interaction)
- 共线性(collinearity)
- 样本独立性(independence)

专题一:回归与混合效应(多水平/层次/嵌套)模型
1.1一般线性模型(lm)
1)基本形式、基本假设、估计方法、参数检验、模型检验
2)一般线性回归、方差分析及协方差分析
3)一般线性回归模型验证
4)一般线性回归模型选择-逐步回归
案例1:鱼类游速与水温关系的回归及协方差分析;
案例2:施肥和种植密度对作物产量的影响
案例3:决定海洋植食性鱼类多样性的决定因子-模型验证
案例4:淡水鱼丰度的环境因子的筛选-逐步回归

1.2广义线性模型(glm)
1) 基本形式、基本假设、估计方法、参数检验、模型检验
2) 0,1数据分析:伯努利分布、二项分布及其过度离散问题
3)计数数据各种情况及模型选择:泊松、伪泊松、负二项、零膨胀泊松、零膨胀负二项、零截断泊松及零截断负二项模型
4) 广义线性模型的模型比较和选择-似然比LR和AIC
案例1:动物身体特征与患病与否(0,1)的关系的逻辑斯蒂回归
案例2:海豹年龄与攻击行为的关系-0,1数据转化为比率数据分析
案例3:不同实验处理下蚜虫多度的差异分析-计数数据泊松回归
其他案例:零膨胀、零截断数据分析。。。。。。。。。。。。。。。。。。。。

1.3线性混合效应模型(lmm)
1) 线性混合效应模型基本原理
2) 线性混合效应模型建模步骤及实现
3) 线性混合效应模型的预测和模型诊断
4) 线性混合效应模型的多重比较
案例1:睡眠时间与反应速度关系
案例2:多因素实验(分层数据)的多重比较

1.4广义线性混合效应模型(glmm)
1)广义线性混合效应模型基本原理
2)广义线性混合效应模型建模步骤及流程
3)广义线性混合效应模型分析0,1数据
4)广义线性混合效应模型分析计数数据及模型选择:泊松、伪泊松、负二项、零膨胀泊松、零膨胀负二项、零截断泊松及零截断负二项模型
案例1:蝌蚪“变态”与否(0,1)的多因素分析-逻辑斯蒂混合效应模型
案例2:虫食种子多度影响因素的多变量分析-泊松混合效应模型
案例3:模拟计数数据-零膨胀、零截断、过度离散等广义混合效应模型

专题二:贝叶斯(brms)回归与混合效应(多水平/层次/嵌套)模型
2.1贝叶斯回归及混合效应模型上
1)贝叶斯回归分析简介
2)利用brms实现贝叶斯回归分析简介
3)贝叶斯回归分析的模型诊断、交叉验证、预测和作图
4)贝叶斯广义线性模型实现:gamma分布、伯努利分布、二项分布等
案例1:鱼游速与温度关系的贝叶斯回归-结果解读、模型验证、模型诊断
案例2:森林生物量与林龄关系贝叶斯回归-gamma分布、brms参数调整
案例3:动物身体特征与患病与否(0,1)的关系的贝叶斯回归-伯努利分布
案例4:海豹年龄与攻击行为的关系-0,1数据转化为比率数据分析-二项分布
其他案例:贝叶斯分析计数数据过度离散、零膨胀等问题

2.2贝叶斯回归及混合效应模型下
1)贝叶斯线性混合效应模型:实现步骤、模型验证、多重比较
2)贝叶斯广义混合效应模型-计数数据分析:泊松、负二项、零膨胀泊松、零膨胀负二项等
案例1:睡眠时间与反应速度关系的贝叶斯线性混合效应模型
案例2:教师受欢迎程度的多变量预测-贝叶斯线性混合效应模型
案例3:虫食种子多度(计数数据)影响因素的多变量分析-贝叶斯广义混合效应模型
其他案例:贝叶斯分析计数数据过度离散、零膨胀等问题

专题三:相关数据回归分析:嵌套、时间、空间、系统发育相关数据分析
3.1嵌套型随机效应混合效应模型分析及贝叶斯实现
1)数据分层问题及嵌套型随机效应混合效应模型介绍
2)嵌套型随机效应混合效应模型分析步骤及流程及模型选择(MuMIn)
3)嵌套型随机效应混合效应模型的方差分解:ICC、varcomp及贝叶斯法
4)经典方差分解案例讲解
案例1:不同种类海豚年龄多因素预测模型及模型选择(MuMIn)- 嵌套结构
案例2:纲/科/属/种型嵌套随机效应的方差分解及贝叶斯方法
案例3:物种属性可塑性和基因多样性对物种丰富度影响的相对贡献-全模型变差分解

3.2时间相关数据分析及贝叶斯实现
1)回归模型的方差异质性问题及解决途径
2)时间自相关分析:线性及混合效应模型及贝叶斯方法
3)时间自相关+方差异质性分析及贝叶斯实现
案例1:模拟数据方差异质性问题-gls,lmm及brms方法比较
案例2:鸟类多度变化的时间自相关分析-gls vs brms
案例3:资源脉冲与食谱关系分析:方差异质性+时间相关-lmm vs brms

3.3空间相关数据分析及贝叶斯实现
1)空间自相关概述
2)空间自相关问题解决方式:自相关修正参数、空间距离权重法、空间邻接权重法
3)空间自相关问题修正基本流程-gls和lme
4)空间自相关贝叶斯修正-空间距离权重 VS 空间邻接权重
案例1:北方林物种多样性与气候关系-一般线性回归模型空间自相关问题修正
案例2:全球水鸟巢穴捕食率影响因素分析-混合效应模型空间自相关问题修正

3.4系统发育相关数据分析及贝叶斯实现
1、系统发育简介:系统发育假说、系统发育信号及系统发育树
2、系统发育树及系统发育距离矩阵构建
3、系统发育信息纳入回归模型-广义最小二乘(gls)
4、系统发育信息纳入混合效应模型(lmm/glmm)及贝叶斯方法实现案例
案例1:模拟数据-系统发育相关对物种属性影响-gls vs brms
案例2:全球水鸟巢穴捕食率影响因素分析-系统发育混合效应模型:lmm vs brms

专题四:非线性关系数据分析:广义可加(混合)模型(GAM/GAMM)和非线性(混合)(NLM/NLMM)模型
4.1“线性”回归的含义及非线性关系的判定
4.2广义可加(混合效应)(GAM/GAMM)模型及贝叶斯实现
4.3非线性(混合效应)(NLM/NLMM)模型及贝叶斯实现

原文链接:
https://mp.weixin.qq.com/s?__biz=MzUyNzczMTI4Mg==&mid=2247615880&idx=5&sn=9dde4dcc335af6bac18dccc8dc2fc5cf&chksm=fa785ab5cd0fd3a32cb23d4d49aebfa20604b09df72402a97a5c23a9aead15047d709e5567d7&token=807046653&lang=zh_CN&scene=21#wechat_redirect
相关文章:

R语言混合效应(多水平/层次/嵌套)模型及贝叶斯实现技术应用
回归分析是科学研究中十分重要的数据分析工具。随着现代统计技术发展,回归分析方法得到了极大改进。混合效应模型(Mixed effect model),即多水平模(Multilevel model)/分层模型(Hierarchical Model)/嵌套模…...
[C++]使用C++部署yolov9的tensorrt模型进行目标检测
部署YOLOv9的TensorRT模型进行目标检测是一个涉及多个步骤的过程,主要包括准备环境、模型转换、编写代码和模型推理。 首先,确保你的开发环境已安装了NVIDIA的TensorRT。TensorRT是一个用于高效推理的SDK,它能对TensorFlow、PyTorch等框架训…...

eureka注册中心做了哪些事情/原理?
1.服务注册: 将eureka client发送过来的元数据存储到注册表中 2.服务续约: eureka client默认会每30秒向eureka server发送一次心跳来进行服务续约,通过这一行动来表示自己没有出现故障; 3.服务…...

c语言经典测试题4
1.题1 #include <stdio.h>//没有break的话,输入什么都会往下一直执行下去,而且default在最后就会全都执行 int main() {char c;int v0 0, v1 0, v2 0;do{switch (c getchar())// 输入ADescriptor{casea:caseA:casee:caseE:casei:caseI:caseo:…...
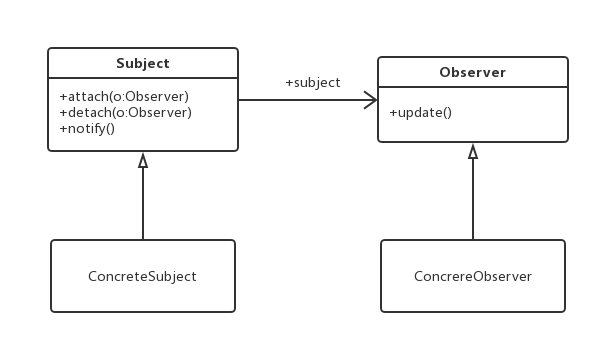
设计模式(五)-观察者模式
前言 实际业务开发过程中,业务逻辑可能非常复杂,核心业务 N 个子业务。如果都放到一块儿去做,代码可能会很长,耦合度不断攀升,维护起来也麻烦,甚至头疼。还有一些业务场景不需要在一次请求中同步完成&…...

MySQL-七种SQL优化
一、插入数据 普通插入: 采用批量插入(一次插入的数据不建议超过1000条) insert into tb_test values(1,Tom),(3, Cat),(3, Jerry)....手动提交事务 start transaction; insert into tb_test values(1,Tom),(3, Cat),(3, Jerry); insert …...

针对Umi、React中遇到的 “xxxx”不能用作 JSX 组件 问题解决方案
一、处理方案 这是因为"types/react"、"types/react-dom"在子依赖中使用的版本不一致导致,一般情况npm会自动帮我们处理版本不一致的问题。如果npm处理不了,就需要我们自己手动处理在package.json中添加一项配置 {name:"test&…...

蓝桥杯备战刷题one(自用)
1.被污染的支票 #include <iostream> #include <vector> #include <map> #include <algorithm> using namespace std; int main() {int n;cin>>n;vector<int>L;map<int,int>mp;bool ok0;int num;for(int i1;i<n;i){cin>>nu…...
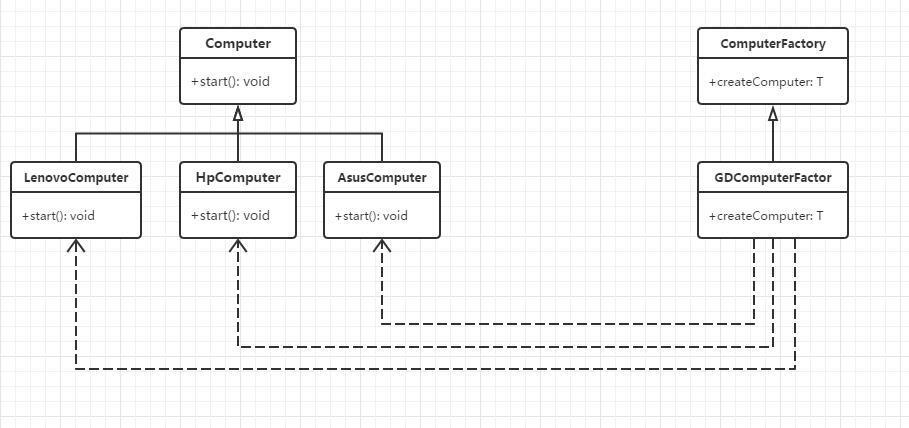
设计模式(十) - 工厂方式模式
前言 在此前的设计模式(四)简单工厂模式中我们介绍了简单工厂模式,在这篇文章中我们来介绍下工厂方法模式,它同样是创建型设计模式,而且又有些类似,文章的末尾会介绍他们之间的不同。 1.工厂方法模式简介 …...

http协议基础与Apache的简单介绍
一、相关介绍: 互联网:是网络的网络,是所有类型网络的母集因特网:世界上最大的互联网网络。即因特网概念从属于互联网概念。习惯上,大家把连接在因特网上的计算机都成为主机。万维网:WWW(world…...
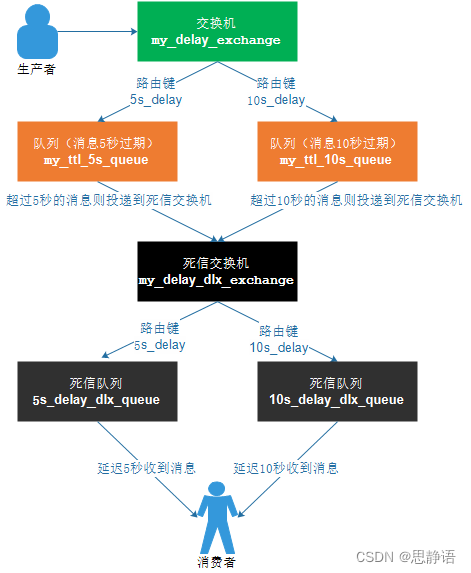
RabbitMQ的死信队列和延迟队列
文章目录 死信队列如何配置死信队列死信队列的应用场景Spring Boot实现RabbitMQ的死信队列 延迟队列方案优劣:延迟队列的实现有两种方式: 死信队列 1)“死信”是RabbitMQ中的一种消息机制。 2)消息变成死信,可能是由于…...

PyQt 逻辑与界面分离
将逻辑与界面分离是一种良好的软件设计实践,可以提高代码的可维护性和可扩展性。在使用 pyuic 工具转换 Qt Designer 的 .ui 文件时,你可以通过以下方式实现逻辑与界面的分离: 创建一个单独的 Python 模块,用于编写主窗口的逻辑代…...

opengl播放3d pose 原地舞蹈脚来回飘动
目录 opengl播放3d pose 原地舞蹈脚来回飘动 设置相机视角 opengl播放3d pose 原地舞蹈脚来回飘动 opengl播放3d pose 原地舞蹈时,脚来回飘动,正常状态是脚应该不动的。 经过反复分析实验验证,找到原因是,渲染计算3d坐标时,都要减去一个offset,这个offset是髋关节的坐…...
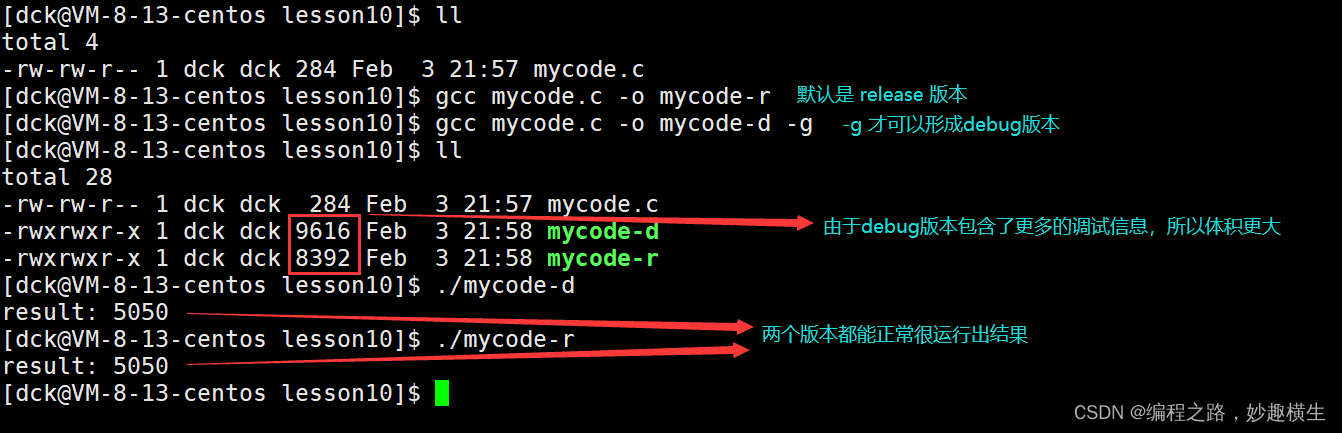
Linux环境基础开发工具使用篇(三) git 与 gdb
一、版本控制器-git 1.简单理解: ①git既是服务端,又是客户端 ②git会记录版本的变化 ③git是一个去中心化的分布式软件 git/gitee 是基于git仓库搭建的网站,让版本管理可视化 2.git 三板斧提交代码 查看安装的git版本 git--version 命令行提交代…...

mybatis---->tx中weekend类
🙌首先weekend可不是mybatis中的类呦~~🙌 它是来自于mybatis的一个扩展库! 如果你要在springboot中使用,需要引入以下依赖~~ <dependency><groupId>tk.mybatis</groupId><artifactId>mapper-spring-boot…...

Shell echo、printf、test命令
目录 Shell echo命令 打印文本消息 显示变量值 输出特殊字符 输出到文件 追加到文件 Shell printf 命令 打印简单文本 Shell test 命令 文件测试 字符串比较 整数比较 逻辑运算 Shell echo命令 打印文本消息 echo "Hello, World!" 显示变量值 name&q…...

腾讯云主机Ubuntu22.04安装Odoo17
一、安装PostgreSQL16 参见之前的文章 Ubuntu22.04安装PostgreSQL-CSDN博客 二、安装Odoo17 本方案使用的nightly版的odoo,安装的都是最新版odoo wget -O - https://nightly.odoo.com/odoo.key | apt-key add - echo "deb http://nightly.odoo.com/17.0/n…...

conda常用命令详解
Conda 是一个功能强大的包管理器和环境管理器,用于安装、部署和管理软件包和其依赖关系。下面是一些常用的 Conda 命令及其详细解释: 创建环境: conda create --name myenv python3.8可以指定创建环境的目录conda create --prefix /path/to/d…...
Java面试——锁
公平锁: 是指多个线程按照申请锁的顺序来获取锁,有点先来后到的意思。在并发环境中,每个线程在获取锁时会先查看此锁维护的队列,如果为空,或者当前线程是等待队列的第一个,就占有锁,否则就会…...
Spring Boot与Netty:构建高性能的网络应用
点击下载《Spring Boot与Netty:构建高性能的网络应用》 1. 前言 本文将详细探讨如何在Spring Boot应用中集成Netty,以构建高性能的网络应用。我们将首先了解Netty的原理和优势,然后介绍如何在Spring Boot项目中集成Netty,包括详…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...
