数学建模【插值与拟合】
一、插值与拟合简介
在数学建模过程中,通常要处理由试验、测量得到的大量数据或一些过于复杂而不便于计算的函数表达式,针对此情况,很自然的想法就是,构造一个简单的函数作为要考察数据或复杂函数的近似。插值和拟合就可以解决这样的问题。
给定一组数据,需要确定满足特定要求的曲线,如果所求曲线通过所给定有限个数据点,这就是插值。有时由于给定的数据存在测量误差,往往具有一定的随机性。因而,要求曲线通过所有数据点不现实也不必要。如果不要求曲线通过所有数据点,而是要求它反映对象整体的变化态势,得到简单实用的近似函数,这就是曲线拟合。
插值和拟合都是根据组数据构造一个近似函数, 但由于近似的要求不同,二者在数学方法上是完全不同的。而面对个实际问题,究竞应该用插值还是拟合,有时容易确定,有时并不明显。
由于插值和拟合是一种手段,并无绝对的适用赛题,也并不算是一种模型,故本篇没有适用赛题、模型流程、流程解析部分。后面将重于使用,分别介绍插值和拟合的操作。
二、插值
1.一维插值
①基本概念
已知未知函数在n+1个互不相同的观测点x0<x1<...<xn处的函数值(或观测值):
yi = f(xi) , i = 0, 1, ..., n
寻求一个近似函数(即近似曲线)中φ(x) ,使之满足
φ(xi) = yi, i = 0, 1, ..., n
即求一条近似曲线φ(x),使其通过所有数据点(xi, yi) i = 0, 1, ..., n
对任意非观测点X(X ≠ xi, i = 0,1, ..., n),要估计该点的函数值f(X),就可以用φ(X)的值作为f(X)的近似估计值,即φ(X) ≈ f(X)。通常称此类建模问题为插值问题,而构造近似函数的方法就称为插值方法。
观测点xi(i = 0, 1, ..., n)称为插值节点,f(x)称为被插函数或原函数,φ(x)为插值函数,φ(xi) = yi称为插值条件,含xi(i = 0, 1, ..., n)的最小区间[a, b](a = min{xi}, b = max{xi})称为插值区间,X称为插值点,φ(X)为被插函数f(x)在X ∈ [a, b] 点处的插值。
这里对于多项式插值,拉格朗日插值、牛顿插值等方法理论部分不做介绍,有兴趣的同学自行查阅。
②函数使用
Ⅰinterp1函数
MATLAB中一维函数interp1的调用格式为
vq = interp1(x0, y0, xq, method, extrapolation)-
x0:已知的插值节点
-
y0:对应x0的函数值
-
xq:欲求函数值的节点坐标
-
vq:求得的节点xq处的函数值
-
method:指定插值的方法,默认为线性插值。其值常用的有:
| 'nearest' | 最近邻插值 |
| 'linear' | 线性插值 |
| 'spline' | 三次样条插值,函数是二次光滑的 |
| 'cubic' | 立方插值,函数是一次光滑的 |
MATLAB2020A不提倡使用函数interp1,建议使用函数griddedInterpolant。
ⅡgriddedInterpolant函数
函数griddedInterpolant适用于任意维数的插值。
一维插值的调用格式为
F = griddedInterpolant(x, v, method, extrapolation)计算对应的函数值的使用格式为
vq = F(xq)n维插值的调用格式为
F = griddedInterpolant(x1, x2,..., xn, v, method, extrapolation)计算对应的函数值的使用格式为
vq = F(xq1, xq2,..., xqn)Ⅲcsape三次样条插值函数
三次样条插值还可以使用函数ecsape,csape的返回值是pp形式。求插值点的函数值,调用函数fnval。
pp = csape(x0, y0)使用默认的边界条件,即拉格朗日边界条件。
pp = csape(x0, y0, conds, valconds)中的conds指定插值的边界条件,详细见官网
利用pp结构的返回值,还可以计算返回值函数的导数和积分,命令分别为fnder,fnint,这两个函数的返回值还是pp结构。
| 调用格式 | 函数功能 |
| pp1 = csape(x0, y0) | 计算插值函数 |
| pp2 = fnder(pp1) | 计算pp1对应函数的导数,返回值pp2也是pp结构 |
| pp3 = fnint(pp1) | 计算pp1对应函数的积分,返回值pp3也是pp结构 |
| y = fnval(pp1, x) | 计算pp1对应的函数在x点的取值 |
2.二维插值
①基本概念
二维插值的基本概念和一维差不多,只不过曲线变成了曲面而已,不做赘述。
②网格数据的插值
已知m×n个节点(xi, yi, zij)(i = 1, 2,.., m; j = 1, 2, ..., n),且x1 <...< xm; y1 < ...< yn。求点(x, y)处的插值z。
Ⅰinterp2函数
z = interp2(x0, y0, z0, x, y, 'method')-
x0,y0:m维和n维向量,表示插值节点
-
z0:n×m矩阵,表示对应插值节点函数值
-
x,y:一维数组,表示插值点。x与y应是方向不同的向量,即一个是行向量,另一个是列向量
-
z:矩阵,行数为y的维数,列数为x的维数,表示得到的插值
-
method:用法同上面的一维插值
如果是三次样条插值,可以使用函数griddedInterpolant和csape。函数girddedInterpolant前面已经介绍过。
Ⅱcsape函数
pp = csape({x0, y0}, z0, conds, valconds);
z = fnval(pp, {x, y})-
x0,y0:分别为m维和n维向量
-
z0:m×n矩阵
-
z:矩阵,行数为y的维数,列数为x的维数,表示得到的插值
③散乱数据的插值
已知n个插值节点(xi, yi, zi)(i =1, 2, ..., n),求点(x, y)处的插值z。
Ⅰgriddata函数
函数griddata的调用格式为
ZI = griddata(x, y, z, XI, YI)-
x,y,z:均为n维向量,指明所给数据点的横坐标、纵坐标和竖坐标
-
XI,YI:给定的网格点的横坐标和纵坐标
-
ZI:网格(XI, YI)处的函数值。XI与YI应是方向不同的向量,即一个是行向量,另一个是列向量
ⅡscatteredInterpolant函数
函数scatteredInterpolant的调用格式为
Fz = scatteredInterpolant(x0, y0, z0, Method, ExtrapolationMethod);-
返回值Fz是结构数组,相当于给出了插值函数的表达式
- x0,y0,z0:分别为已知n个点的x,y,z坐标
- Method:插值方法
- ExtrapolationMethod:区域外部节点的外插方法
要计算插值点(x, y)处的值,调用Fz即可
z = Fz(x, y);三、拟合
1.线性最小二乘法
①解线性方程组拟合参数
要拟合等式中的参数a1, a2, ..., am,把观测值代入等式,得到线性方程组
RA = Y
则A = pinv(R) * Y或简化格式A = R \ Y
②约束线性最小二乘解
在最小二乘意义下解约束线性方程组
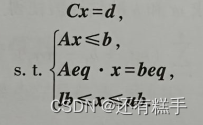
即求解数学规划问题
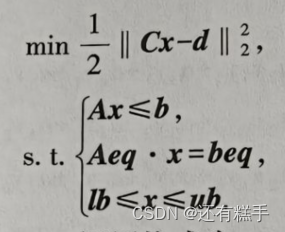
求解上述问题调用函数lsqlin
x = lsqlin(C, d, A, b, Aeq, beq, lb, ub);③多项式拟合
多项式拟合的函数为polyfit,调用格式为
p = polyfit(x, y, n) % 拟合n次多项式,返回值p是多项式对应的系数,排列次序为从高次幂系数到低次幂系数计算多项式p在x处的函数值
y = polyval(p, x);2.fittype和fit函数
函数fit需要和函数fittype配合使用,fittype用于定义拟合的函数类,fit进行函数拟合。fit既可以拟合一元或二元线性函数,也可以拟合一元或二元非线性函数。 这里介绍这两个函数的调用格式。
fittype的调用格式为
aFittype = fittype(libraryModeName) % 利用库模型定义函数类
aFittype = fittype(expression, Name, Value) % 利用字符串定义函数类
aFittype = fittype(linearModeTerm, Name, Value) % 利用基函数的线性组合定义函数类
aFittype = fittype(anonymousFunction, Name, Value) % 利用匿名函数定义函数类函数fit的调用格式为
fitobject = fit(x, y, aFittype) % x和y分别为自变量和因变量的观测值列向量,返回值fitobject为拟合函数的信息
fitobject = fit([x, y], z, aFittype) % [x, y]为自变量的观测值的两列矩阵,z为因变量的观测值列向量,这里是拟合二元函数
[fitobject, gof] = fit(x, y, aFittype, Name, Value) % 返回值gof为结构数组,给出了模型的一些检验统计量3.非线性拟合
MATLAB非线性拟合的主要函数有fit和lsqcurvefit,fit函数使用很方便,但只能拟合一元和二元函数,lsqcurvefit可以拟合任意多个自变量的函数,并且可以约束未知参数的上界和下界,下面用例子讲解。
①fit函数
用下表数据拟合函数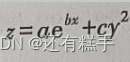
| x1 | 6 | 2 | 6 | 7 | 4 | 2 | 5 | 9 |
| x2 | 4 | 9 | 5 | 3 | 8 | 5 | 8 | 2 |
| y | 14.2077 | 39.3622 | 17.8077 | 11.8310 | 32.8618 | 16.9622 | 33.0941 | 11.1737 |
xy0 = d([1, 2], :)';
z0 = d(3, :)';
g = fittype('a * exp(b * x) + C*y^2', 'dependent' ,'z' , 'independent', {'x', 'y'});
[f, st] = fit(xy0, z0, g, 'StartPoint', rand(1,3));求得z=6.193e的0.04353x次方+0.3995y²
拟合优度R² = 0.9995,拟合的剩余标准差RMSE = 0.2970,拟合效果很好。
②lsqcurvefit函数
要拟合函数y = f(θ, x),给定x的观测值xdata,y的观测值ydata,求参数向量θ,使得误差平方和最小。
lsqcurvefit函数的调用格式为
theta = lsqcurvefit(fun, theta0, xdata, ydata, lb, ub, options)- fun:定义函数f(θ, x)的M函数或匿名函数
- thata0:θ初始值
- lb,ub:参数θ的下界和上界
- options:设置计算过程的一些算法
- theta:拟合参数θ的值
本篇只是很浅显地介绍了各个函数,每个函数的具体用法和参数设置有兴趣的同学可以到官网查询。如果对其中原理理论部分感兴趣也可以查文献搜索。
相关文章:
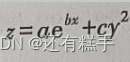
数学建模【插值与拟合】
一、插值与拟合简介 在数学建模过程中,通常要处理由试验、测量得到的大量数据或一些过于复杂而不便于计算的函数表达式,针对此情况,很自然的想法就是,构造一个简单的函数作为要考察数据或复杂函数的近似。插值和拟合就可以解决这…...

汽修专用产品---选型介绍 汽修示波器 汽车示波器 汽车电子 汽修波形 汽车传感器波形 汽车检测
为了满足汽车电子用户的测量需求,我司特推出汽修专用版示波器,一键测量,轻松找出汽车问题。 LOTO各种型号的示波器其实都可以用作汽车传感器信号波形的检测。汽修应用中,工程师对示波器的性能要求对于LOTO产品来说不算高。 在我们…...

如何将简历项目部署到自己的域名下
通过上一篇文章我们得知如何在Github上Fork项目到自己账号下,还有学会配置好简历项目并部署上线,接下来我们就来看一下该项目是如何部署到自己的域名下的 👇 在项目文档中可以看到该简历项目是部署在Vercel上的,首先打开Vercel的官…...

Redisson - 实现Java的Redis分布式和可扩展解决方案
Redisson - 实现Java的Redis分布式和可扩展解决方案 引言: 在现代的分布式系统中,缓存和数据存储扮演着至关重要的角色。Redis作为一种高性能的键值存储数据库,被广泛用于缓存、消息队列、实时数据分析等场景。然而,原生的Redis…...
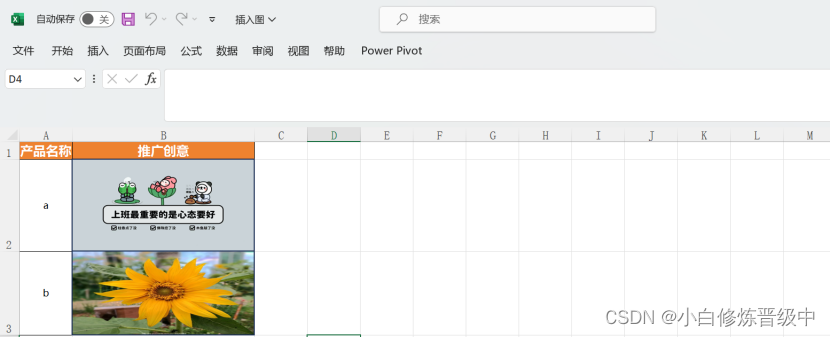
如何利用EXCEL批量插入图片
目录 1.excel打开目标表格; 2.点开视图-宏-录制宏,可以改宏的名字或者选择默认; 3.然后点开视图-宏-查看宏 4.点编辑进去 5.修改代码: (1)打开之后会显示有一堆代码 (2)将这个…...

django rest framework 学习笔记-实战商城3
01用户模块模型定义_哔哩哔哩_bilibili 本博客借鉴至大佬的视频学习笔记 用户模块及商品数据表结构设计 from ckeditor.fields import RichTextField # pip install django-ckeditor from django.db import models# Create your models here. # from wx.richtext import Ri…...

WPF真入门教程29--MVVM常用框架之MvvmLight
1、MVVM模式回顾 关于mvvm模式的基础知识,请看这2个文章: WPF真入门教程23--MVVM简单介绍 WPF真入门教程24--MVVM模式Command命令 做过VUE开发或微信小程序开发的伙伴,就知道MVVM模式,核心就是数据驱动控件,全栈开…...

QT-Day4
思维导图 作业: 头文件 #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QMessageBox> #include <QTimerEvent>//定时器事件类 #include <QTime> #include <QDebug> #include <QPushButton> #include <QT…...
代码随想录算法训练营第三天
● 自己看到题目的第一想法 203.移除链表元素 方法一: 思路: 设置虚拟头节点 dummyhead 设置临时指针 cur 遍历 整个链表 循环: 如果 cur !nullptr &&cur->next !nullptr 则 遍历链表 否则结束遍历 如果 cur->next val 则…...

蓝桥杯刷题1
目录 1. 平方和 2. 门牌制作 3. 卡片 4. 分数 5. 星期一 6. 顺子日期 1. 平方和 题目描述:小明对数位中含有2、0、1、9 的数字很感兴趣,在1 到40 中这样的数包 括1、2、9、10 至32、39 和40,共28 个,他们的和是574&#x…...

前端学习---- 前端HTML基本元素的介绍
一:显示相关的HTML基础知识 1. 推荐的前端编写工具 2. VScode的html速写规则(从a标签开始再用) ①、!:代表生成html的基本框架元素 ②、html元素:直接书写html,不需要加<>,按回车会自动生成 ③、{}…...

力扣思路题:丑数
此题的思路非常奇妙,可以借鉴一下 bool isUgly(int num){if(num0)return false;while(num%20)num/2;while(num%30)num/3;while(num%50)num/5;return num1; }...

C# this关键字的作用
在C#中,this 关键字有以下几种主要作用: 引用当前对象:this 用于引用当前类的实例。可以通过 this 关键字来访问当前对象的成员变量、方法和属性。 class MyClass {private int myVar;public void SetVar(int var){this.myVar var; // 使用…...

Ubuntu18.04虚拟机磁盘扩容-lvm
Ubuntu18.04虚拟机磁盘扩容-lvm 前提虚拟机虚拟磁盘扩容使用新增的磁盘空间扩展vg和lv 前提 没有虚拟机快照虚拟磁盘不是一次性分配空间其它会影响扩容的前置条件 虚拟机虚拟磁盘扩容 此部分不做详细说明。 使用新增的磁盘空间 此节有两种办法,第一种是将新增的…...

低代码开发:数字赋能智能制造的未来
随着数字化转型的深入推进,智能制造已经成为我国制造业发展的重要方向。在这个过程中,低代码开发作为一种高效、便捷的编程方式,正逐渐成为企业数字化转型的得力助手。本文将探讨低代码开发在智能制造领域的应用及价值。 智能制造的挑战 随着…...

janus-gateway的videoroom插件的RTP包录制功能源码详解
引: janus-gateway在配置文件设置后,可以实现对videoroom插件的每个publisher的音频,视频,数据的RTP流录制成mjr文件。 对于音频,视频的mjr文件,可以使用自带的postprocessing工具janus-pp-rec转成mp4文件。 每个pu…...

nginx+keepalived实现nginx高可用集群以及nginx实现Gateway网关服务集群
一、前言 1、简介 Nginx作为一款高性能的Web服务器和反向代理服务器,被广泛使用。且现如今很多高并发场景需要后端服务集群部署,因此nginx也需要支持集群部署从而避免单点故障的问题。 本文将详细介绍使用 KeepalivedNginx 来实现Nginx的高可用集群和N…...

主键、外键、建表范式、MySQL索引、用户管理
1 案例1:主键 1.1 问题 完成如下练习: 练习主键的创建、查看、删除、添加、验证主键练习复合主键的使用练习与auto_increment连用的效果 1.2 方案 主键使用规则: 表头值不允许重复,不允许赋NULL值一个表中只能有一个primary…...
探究前端路由hash和history的实现原理(包教包会)
今天我们来讲一讲前端中很重要的一个部分路由(router),想必前端小伙伴对‘路由’一词都不会感到陌生。但是如果哪天面试官问你,能大概说一说前端路由的实现原理吗? 你又会如何应对呢? 今天勇宝就带着大家一…...

幻兽帕鲁服务器多少钱?有买过的吗?
幻兽帕鲁服务器多少钱?太卷了,降价到24元1个月,阿里云4核16G10M游戏服务器26元1个月、149元半年,腾讯云4核16G游戏服务器32元、312元一年,华为云26元,京东云主机也是26元起。云服务器吧yunfuwuqiba.com给大…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
