算法--动态规划(线性DP、区间DP)
这里写目录标题
- tip
- 数组下标从0开始还是从1开始
- 数学三角形
- 介绍
- 算法思想
- 例题+代码
- 最长上升子序列
- 介绍
- 算法思想
- 例题+代码
- 最长公共子序列
- 介绍
- 算法思想
- 例题+代码
tip
数组下标从0开始还是从1开始
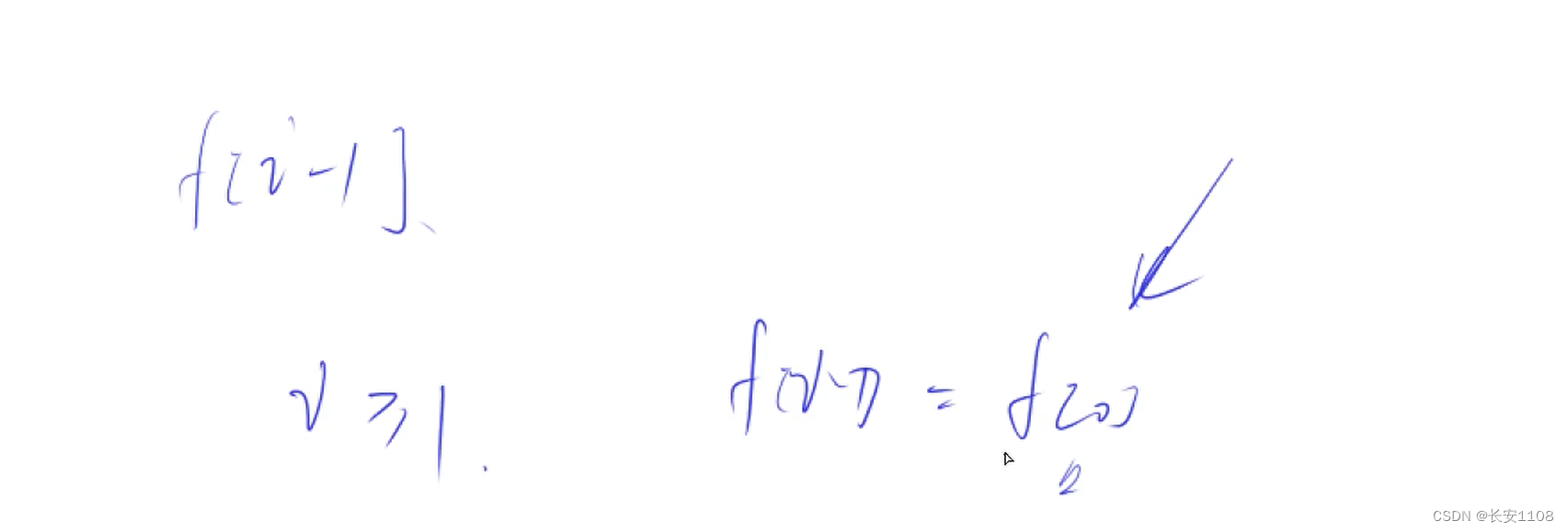
如果代码中涉及到数组下标为i-1(有时候哪怕不是同一个数组也符合情况,因为是针对同一组数据进行的多个数组设置),那么我们可以使 i 从 1开始,这样,当 i = 1 时,就取到了[0],如果这个位置有特殊情况,那么这样一来我们也不必使用 if ,直接对 f [0]设置一个特殊值即可
注意,“输入”与“使用”是统一的,即如果输入数组时决定了使用 i 从 1 开始,那么到时候使用或者取元素时,一定要记得是从 1 开始,
如果输入决定了是从0开始,那么到时候取元素的时候,记得从0开始
数学三角形
介绍
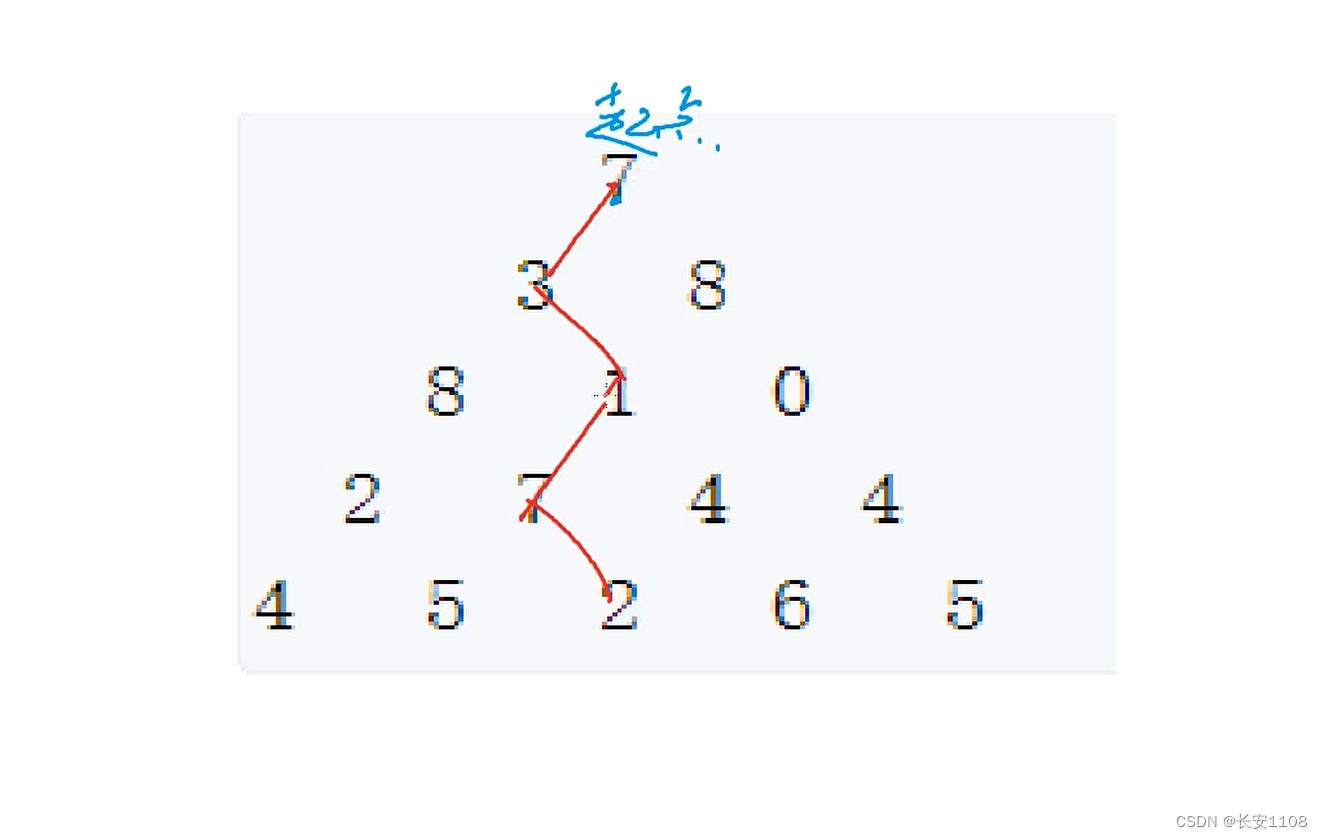
从顶部出发,可以向左下或者右下移动,最后形成一条路径,找到一条路径使得路径上的数字之和最大
算法思想

首先我们对三角形的各个数进行编码,从上到下每行从1开始表上行号,之后,东北方向偏45度进行列号的编排,最左边是1列,之后往右依次是2,3,…,这样一来,我们就可以标定某个元素的位置,这也符合三角形位置的数据在数组内存储时的位置
对于动态规划,仍然是状态表示和状态计算,
状态表示:因为每个元素由一个二维数对进行位置表示,所以,状态表示仍然是一个二维的,如上图所示,属性是max
状态计算:由前面的经验可以总结出:状态计算是一个情况的划分,划分的是上一层的情况,即仅研究上一层即可,之后递推原理会帮助代码完成
上一层的状态有两个,一个来自左上,一个来自右上。
两种划分都是曲线救国的思路,即 f [ i - 1 , j - 1 ] + a[ i , j ],另一个是 f [ i - 1 , j ] + a[ i , j ]
其中 a数组存储了所有的数据,a [ i , j ]就是表示[ i , j ]位置的值
例题+代码
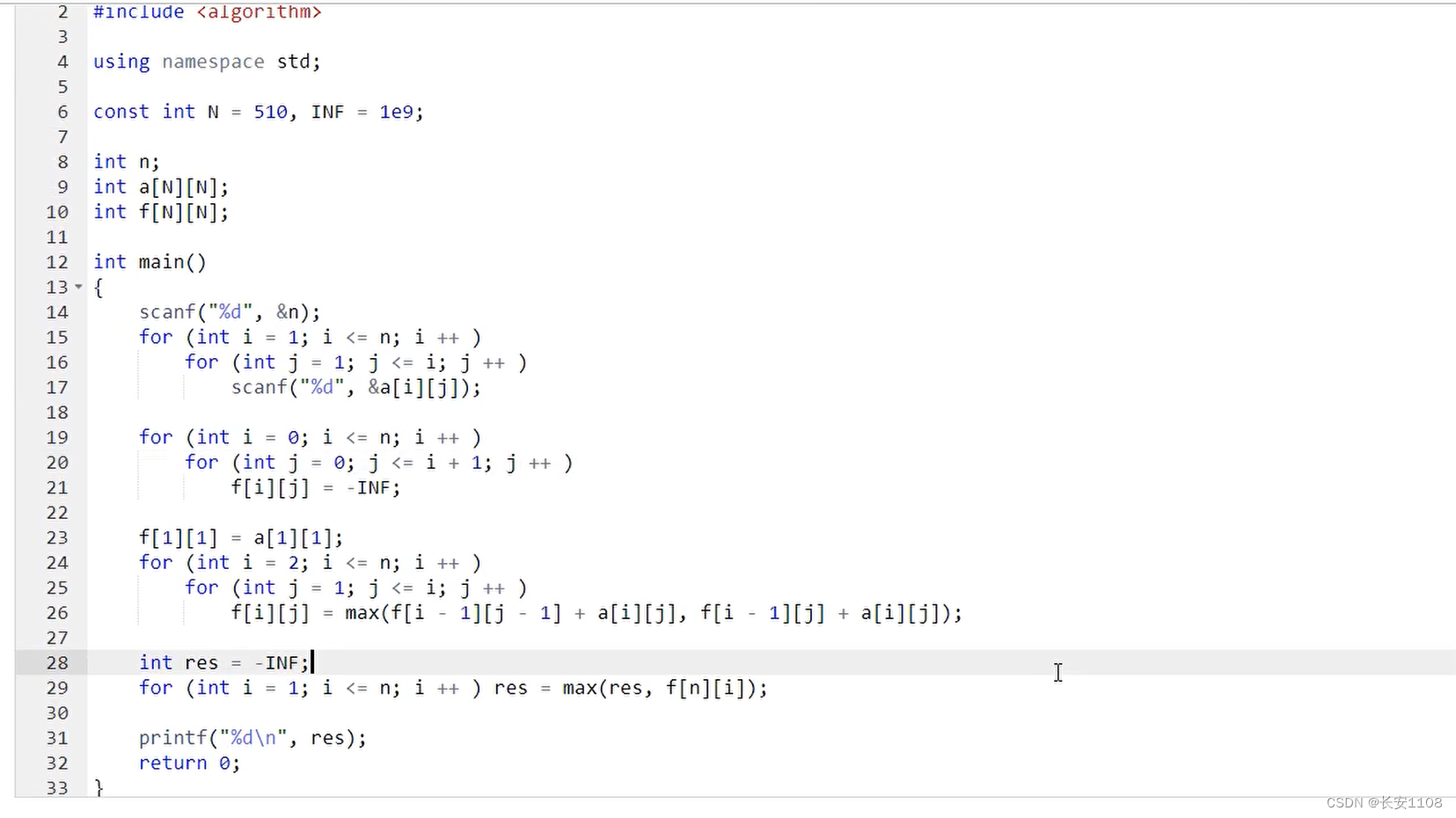
首先,a[N][N]数组是用来存储所有的数据的
f[N][N]是状态表示
之后,main函数里
首先读入n
之后由于这组数据会涉及到 i-1 ,所以使用数组存数据时,i从1开始到小于等于n,j从1开始到小于等于 i (因为是三角形),读入到a[][]数组中,给[0][x] [x][0]这些位置空出来,方便一些特殊情况时拿来使用(包括a数组自己使用或者其他数组使用,总之这个位置要留出来)
之后初始化状态表示,因为状态表示数组涉及到某一点的上边两个角,所以,要处理好边界问题,我们的 i 从 0开始到等于n,j 从 0开始到等于 i + 1 (这样做可以在原来的数据基础上,多加一个0行和0列被初始化,这样的话,当我们遇到如下图所示情况时,就不会出错了),且f[i][j] = - INF,将所有的位置初始化为负无穷,这样的话,最终原数据的外面的位置下标,f[][]的值是负无穷,这样做是为了当我们有路径来到了原数据的外面,那最后的值一定是负无穷,这样我们就可以筛选出来哪些路径是经过了原数据的外面的位置得到的,这些数据可以排除
之后初始化f[1][1] = a[1][1],因为第一个还没有经过任何其他的点,可以初始化为1
之后for循环,i 从 2 开始到等于n(之所以从2开始,是因为1就一个节点,已经被初始化了)
二层循环 ,j 从 1 开始到等于i (仍然是因为输入时是三角形输入)
f[ i ][ j ] = max(f[ i - 1 ][j - 1] + a[ i ][ j ] , f[ i - 1 ][ j ] + a[ i ][ j ])
到此为止,我们就已经可以拿到所有 i j 点的状态了,我们由于是想求最大路径,所以对叶子结点的状态进行求max即可,这里由于之前所有的f都被初始化为了负无穷,所以这样答案也初始化为负无穷去进行比较,而就算有路径经过了负无穷,那最后的值是-INF+一些正数,肯定比-INF要大一点点,所以,res用-INF存储,最后参与到max中
最长上升子序列
介绍


例如这样一个序列,最长子序列就是 1 2 5 6,长度最长是4
算法思想
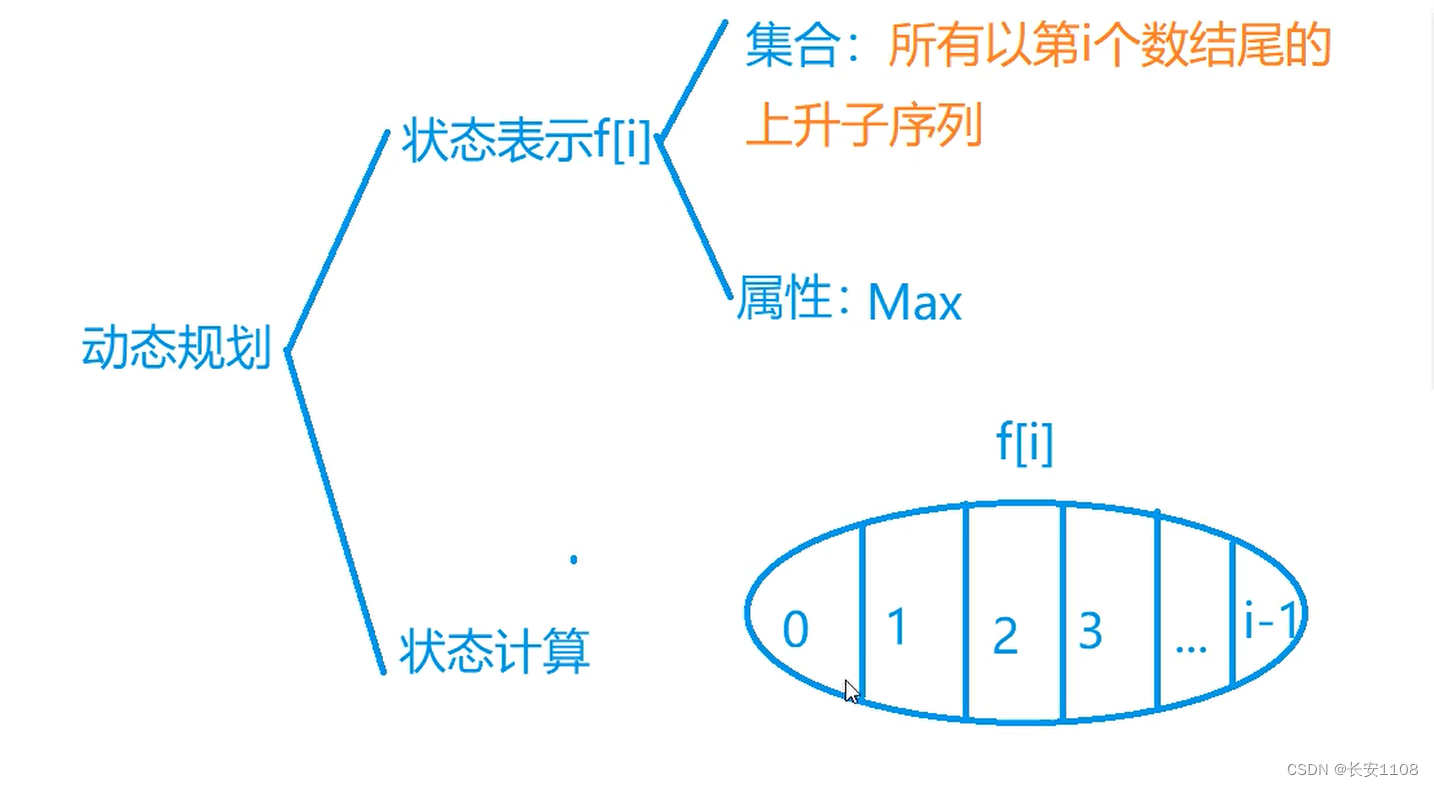
状态表示可以使用一维的,即所有以“第” i 个数结尾的上升子序列,属性是max
状态计算:
划分依据:上一层是第几个数
如果上一层没有数,那么说明只有“第i个数”这一个数
如果上一层的数是第 j 个数,那么可以递推为 f [ j ] + 1(这个j是有条件的,要满足aj < ai)
最后对所有的f[ j ] + 1 (j从0开始到 i - 1)取max就是答案
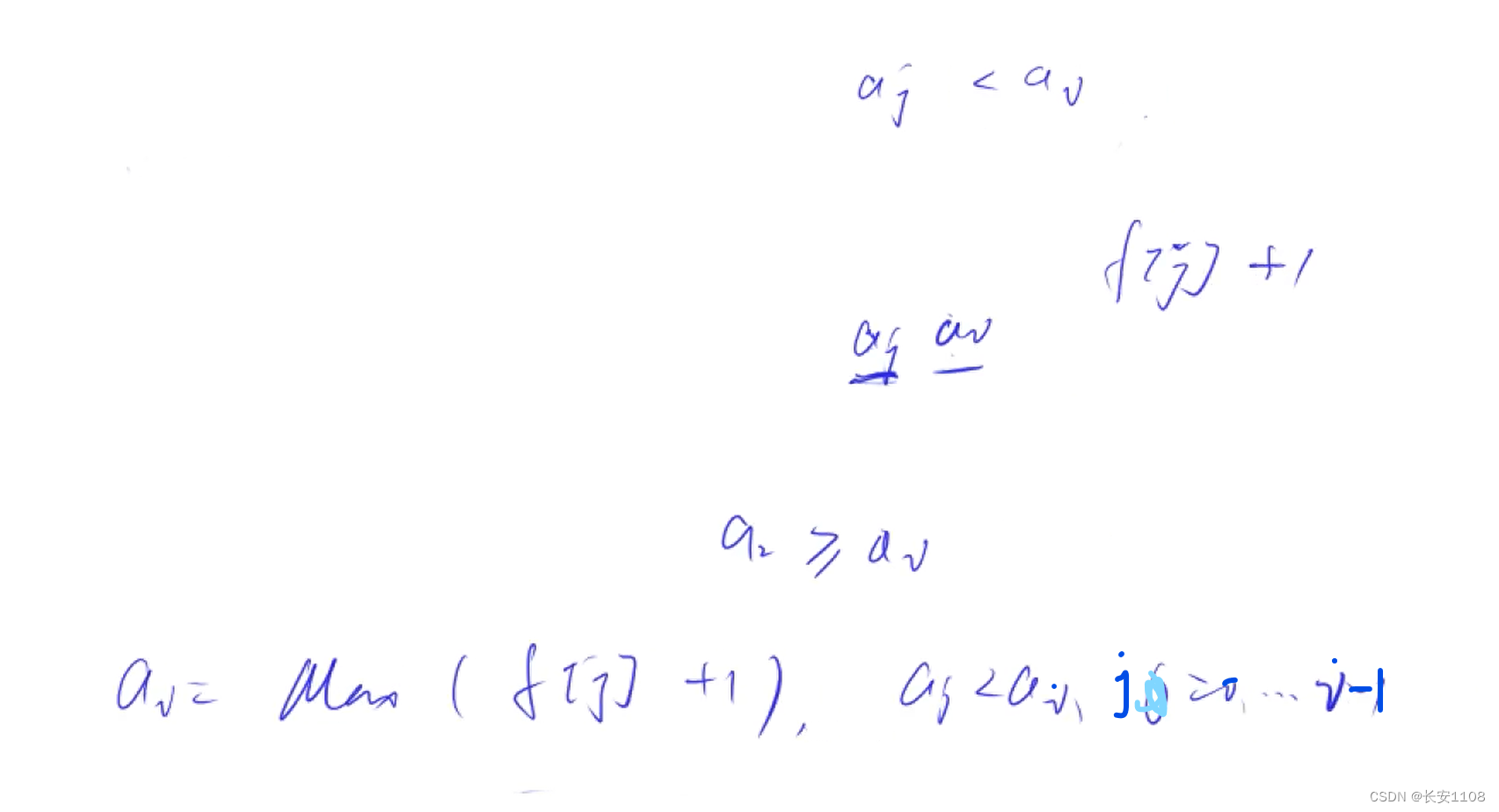
例题+代码
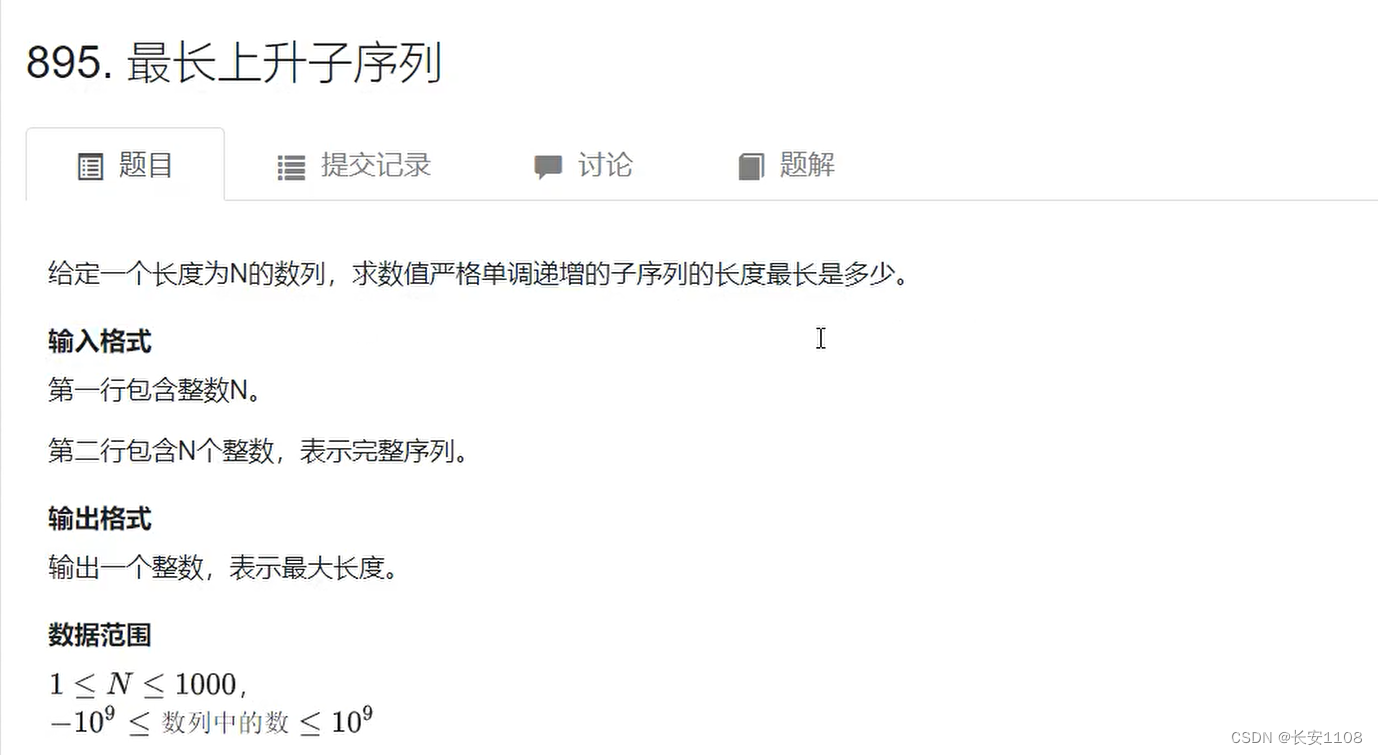
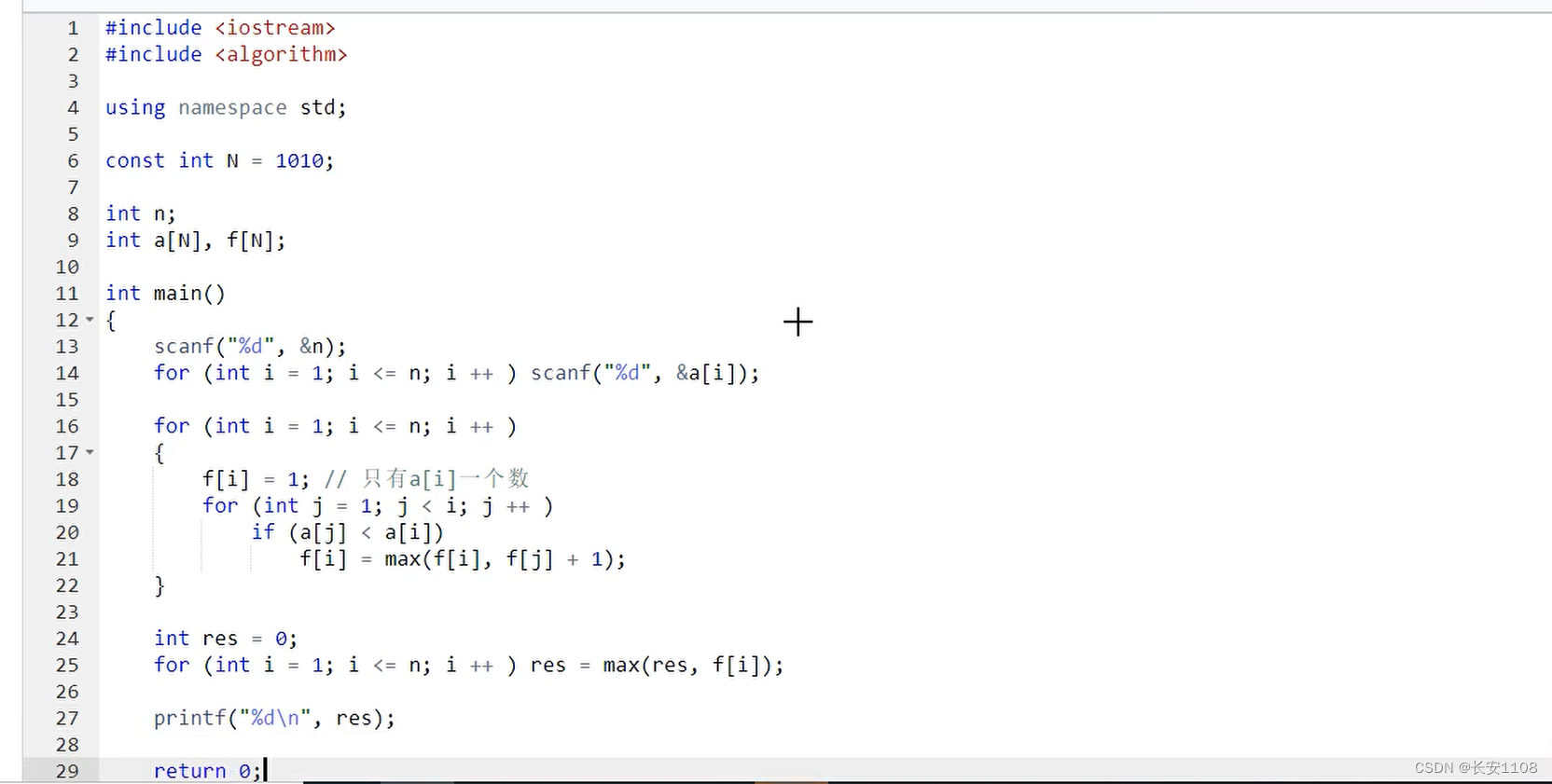
a数组表示将数据进行存储,f数组表示状态表示
在mian函数中
首先输入n
i 从 1 到等于n ,输入a[ i ]
之后对for从1到等于n
f[ i ] = 1 ,(所有的 f 最少是1,所以先初始化为1)
之后,对于for循环,j 从 1 开始到小于 i (因为状态计算时,是以" "前一个数"是第几个数 " 进行划分的,所以j从1到小于i,表示遍历所有划分的情况,为后续取max做准备,这样就可以找到最大的子序列对应的是哪个 j ,因为每个j对应的f[j] 是不同的)
同时判断 if (a[j] < a[i])才是合法的(因为是上升子序列,要求单调)
之后 f[i] = max(f[i] , f[j]+1)(对所有的划分进行max)
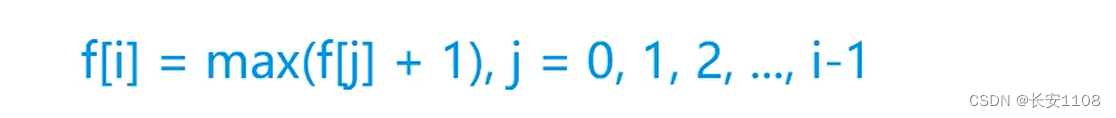
最后,把所有的 f[i] 进行取max,即,将所有的情况取最大值,就是最大子序列
补充:
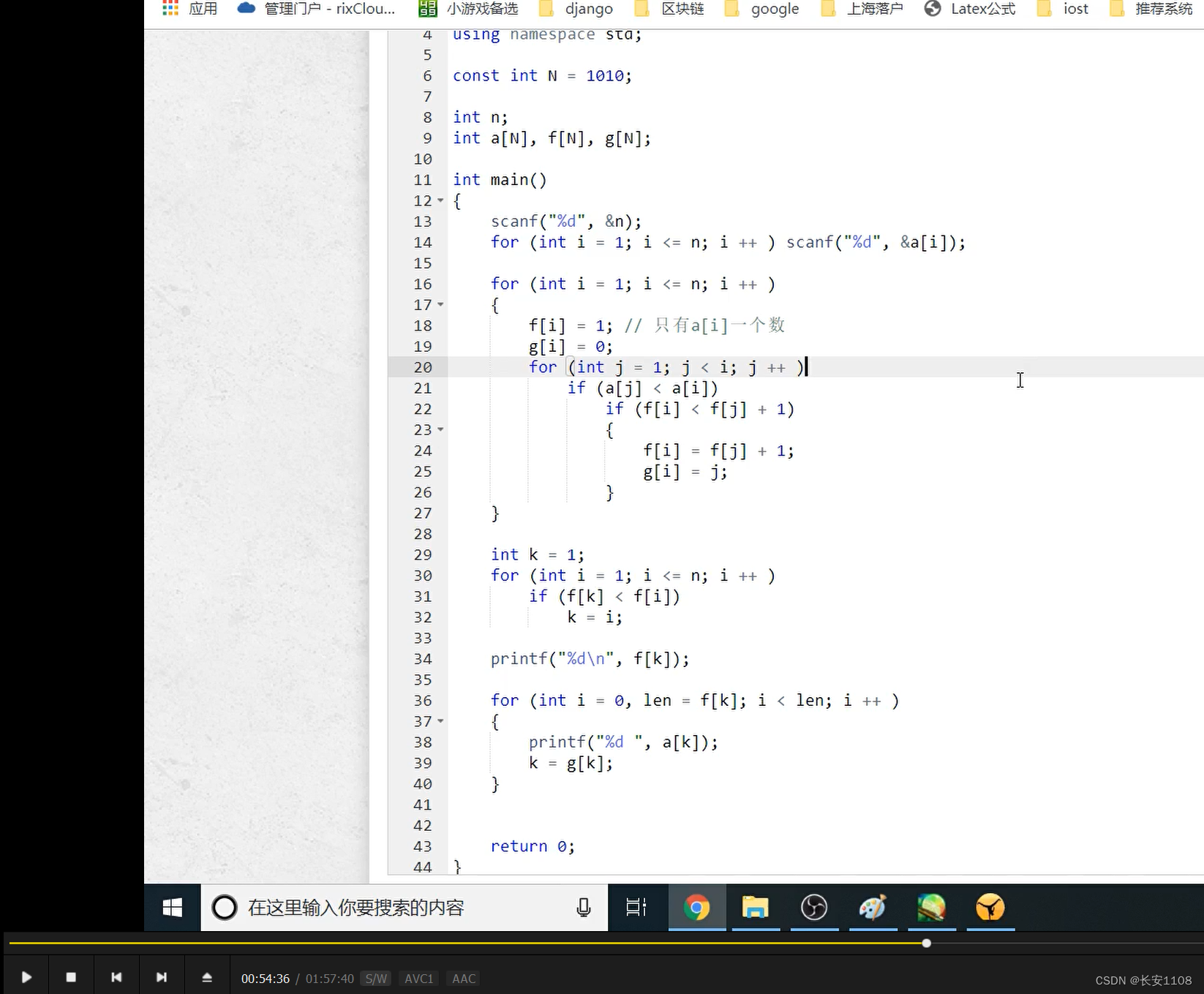
在“动态规划(2)”中00:54时,介绍了如何将最长子序列保存下来
最长公共子序列
介绍

算法思想
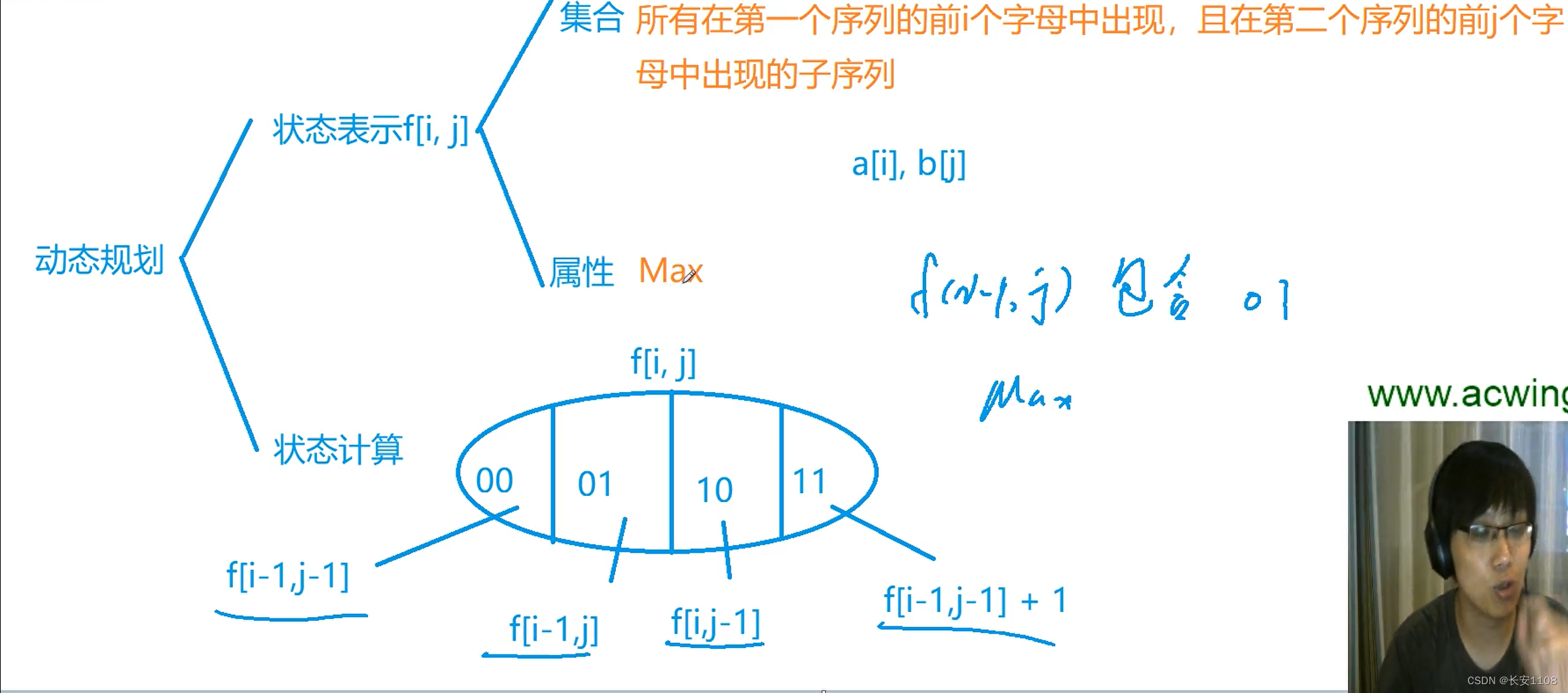
首先,对于状态表示,集合方面,表示所有在第一个序列的前i个字母中出现,且在第二个序列的前 j 个字母中出现的公共子序列,属性是max
之后对于状态计算
可以对公共子序列是否包含a[i] b[j]进行划分,0表示不包含,1表示包含,如上图
之后对于00:
f [ i - 1 , j - 1]
对于11:
f [ i - 1 , j - 1]
对于上面这两个,毫无疑问,确实是这样表示的,
但是对于01和10,我们下面这种表示,是错误的,拿01举例来说,我们想要的是不包含ai但是必须要有bj,而f [i - 1 , j ]表示不包含ai,但是可以有bj也可以没有,所以他是错的,但是f [i - 1 , j ]包含了01这种情况,由于我们是求最大值,而且f的属性也是max,所以,既然f [i - 1 , j ]包含了01的情况,那么就可以拿来进行对比,因为如果对于f [i - 1 , j ]来说,如果01是其所有情况的最大值,那么就符合我们的要求,如果不是,那么我们也没必要再关注01了,而是其他某种情况,所以可以直接用f [i - 1 , j ]。10同理
对于01:
f [i - 1 , j ]
对于10:
f [ i , j - 1 ]
最后补充:
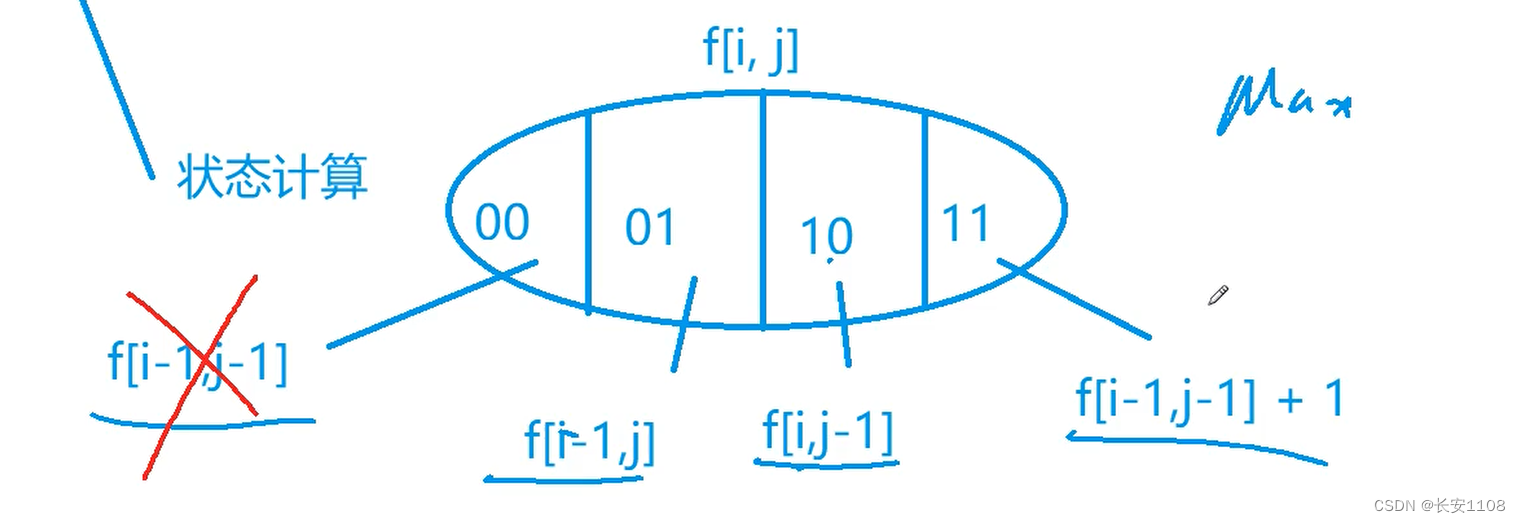
我们在写代码时,不用写00的情况,因为这种情况也被包含在了f [i - 1 , j ]和f [i , j - 1]两种情况里,所以我们在写代码时只需要考虑后面三种情况即可
例题+代码

n和m表示a和b字符串的长度
char a b数组用来存储字符串
f数组是状态表示
之后在main里:
首先输入n 和 m
之后输入字符串,使用%s,以及数组名(这里是数组名+1,可以从数组的第二个位置,也就是下标为1的位置开始将整个字符串都读入,因为代码中出现了i-1)
之后for i 从1~=n
二重循环 j 从1~=m(也就是将所有的 f 进行了遍历)
f[i][j] = max (f[i-1][j] , f[i][j-1]),先将这两个进行取max
之后对11这种情况进行判断
只有当a[i] == b[j]时,才会有第三种情况,所以只有该条件成立,将第三种情况放入max中
最后输出 f[n][m]
相关文章:

算法--动态规划(线性DP、区间DP)
这里写目录标题 tip数组下标从0开始还是从1开始 数学三角形介绍算法思想例题代码 最长上升子序列介绍算法思想例题代码 最长公共子序列介绍算法思想例题代码 tip 数组下标从0开始还是从1开始 如果代码中涉及到数组下标为i-1(有时候哪怕不是同一个数组也符合情况&am…...

【ArcGIS】统计格网中不同土地利用类型占比
基于ArcGIS统计格网中不同土地利用类型占比 数据准备ArcGIS操作步骤1、创建渔网(Create Fishnet)2、建立唯一标识3、选择格网4、提取不同类别土地利用类型5、各类用地面积计算 参考另:可能出现的问题总结Q1:ArcGIS获取唯一值&…...

算法竞赛实用板子
一、声明 自用版参考acwing,致力于实用、好用,板子中有个人理解,持续更新。 二、开板 1.快排 void quick_sort(int q[],int l,int r) {if(l>r)return; //出口int il-1,jr1,xq[lr>>1]; //分治方法while(i<j){do i;w…...

RPA中国 x UiPath | 第六届RPA极客挑战赛,3月16日上海开赛!
随着人工智能技术的不断进步以及数字化转型的深入,企业对于高效、精准、自动化的业务流程需求日益迫切。RPA技术作为连接人类工作与机器操作的桥梁,正逐渐从规则驱动发展为智能决策的助手。 由RPA中国联合UiPath共同主办的【第六届RPA极客挑战赛】将于2…...
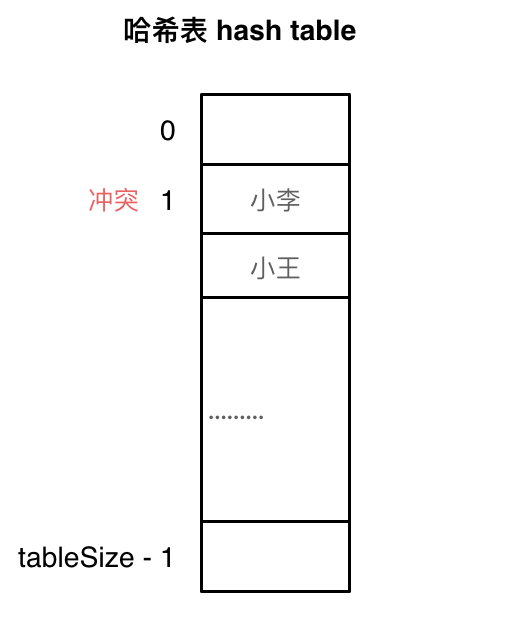
算法打卡day5|哈希表篇01|Leetcode 242.有效的字母异位词 、19.删除链表的倒数第N个节点、202. 快乐数、1. 两数之和
哈希表基础知识 哈希表 哈希表关键码就是数组的索引下标,然后通过下标直接访问数组中的元素;数组就是哈希表的一种 一般哈希表都是用来快速判断一个元素是否出现集合里。例如要查询一个名字是否在班级里: 要枚举的话时间复杂度是O(n)&…...
)
『python爬虫』xpath变化导致无法找到指定元素(持续更新中~)
目录 xpath变化的原因1. 语言设置2. 窗口大小n. 待添加~总结 欢迎关注 『python爬虫』 专栏,持续更新中 欢迎关注 『python爬虫』 专栏,持续更新中 xpath变化的原因 XPath 可能会出现变化的原因有很多,以下是一些常见的情况: 网页…...

人大金仓数据库Kingbase服务SQL基础操作手册
1 kingbase服务 1.1 查看kingbase数据库服务进程 ps -ef|grep kingbase1.2 命令启动kingbase数据库服务 # /opt/Kingbase/ES/V8 为金仓安装目录 # /opt/Kingbase/ES/V8/data 为金仓数据目录 # sys_ctl是数据库服务器启停命令,通过-D选项来来指定数据库数据目录 #…...
赎金信00
题目链接 赎金信 题目描述 注意点 magazine中的每个字符只能在ransomNote中使用一次ransomNote和magazine由小写英文字母组成 解答思路 因为ransomNote和magazine由小写英文字母组成,所以使用大小为26的数组存储magazine中a~z对应出现的次数,ransom…...
如何运行github上的项目
为了讲明白这个过程,特意做了一个相当来说比较好读懂的原理图,希望和我一样初学的小伙伴也能很快上手哈😊 在Github中找到想要部署的项目,这里以BartoszJarocki/CV(线上简历📄)项目为例 先从头…...

机器学习-02-机器学习算法分类以及在各行各业的应用
总结 本系列是机器学习课程的第02篇,主要介绍机器学习算法分类以及在各行各业的应用 本门课程的目标 完成一个特定行业的算法应用全过程: 定义问题(Problem Definition) -> 数据收集(Data Collection) -> 数据分割(Data…...

Java项目学习
一、Java项目学习 1.1 瑞吉外卖(项目提供的资料没笔记) 视频资源:https://www.bilibili.com/video/BV13a411q753/?p1 本人git项目地址:https://gitee.com/xx-xuxin/reggie_take_out.git 瑞吉外卖Day01~Day06没讲的功能(全功能实现…...
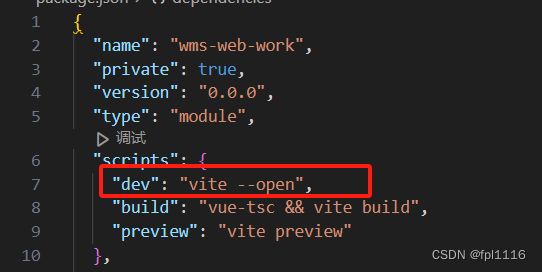
npm run dev和npm run serve两个命令的区别
npm run dev和npm run serve两个命令的区别 前端开发过程中运行Vue项目的时候,有时候使用npm run serve命令可以启动项目,有时候却会报错;有时候使用npm run dev命令可以启动项目,有时候却也会报错。是什么原因造成这种情况呢&am…...
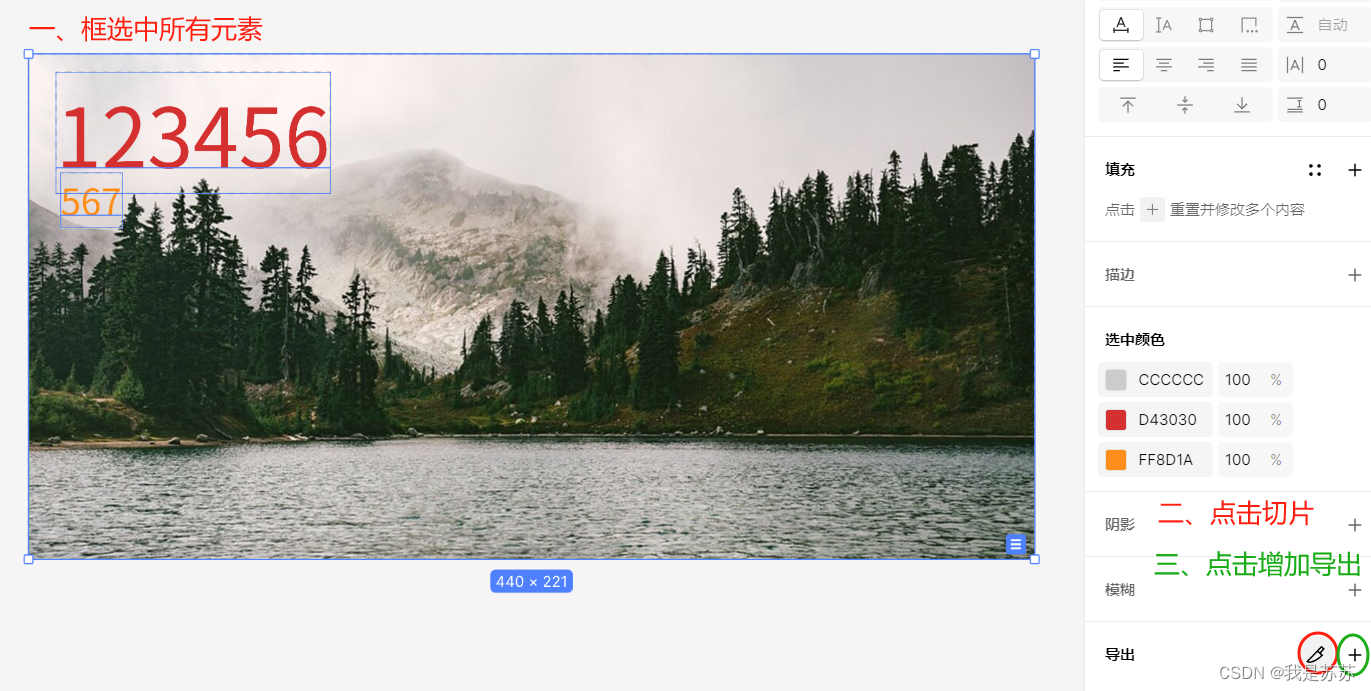
ui设计:利用即使设计设计出漂亮样式
目录 一、基本操作 二、具体介绍 6-1 填充图片 6-2 填充色 6-3 图标 右边栏基础设置 右边栏导出编辑 一、基本操作 二、具体介绍 6-1 填充图片 选择其一图片填充 6-2 填充色 6-3 图标 右边栏基础设置 右边栏导出...

[unity]lua热更新——个人复习笔记【侵删/有不足之处欢迎斧正】
一、AssetBundle AB包是特定于平台的资产压缩包,类似于压缩文件 相对于RESOURCES下的资源,AB包更加灵活轻量化,用于减小包体大小和热更新 可以在unity2019环境中直接下载Asset Bundle Browser 可以在其中设置关联 AB包生成的文件 AB包文件…...

Springboot日常总结-@RestController和@Controller的区别
RestController和 Controlle是两种不同的控制器实现,它们的主要区别在于如何处理返回的数据和是否支持跳转到视图页面。 Controller 是一个基本的控制器注解,它允许你将一个类标记为一个Spring MVC控制器处理器。使用 Controller 的类中的方法可以直接返…...

MongoDB之客户端工具与核心概念及基本类型篇
MongoDB之客户端工具与核心概念及基本类型篇 文章目录 MongoDB之客户端工具与核心概念及基本类型篇1. MongoDB是什么?1. 关于MongoDB2. 相关客户端工具1. MongoDB Compass2. Studio 3T3. Navicat for MongoDB4. NoSQL Manager for MongoDB Professional 2.MongoDB相关概念2.1 …...

Essential C++ 编程基础
Essential C 前言1.1 如何撰写 C程序1.2 对象的定义与初始化1.3 撰写表达式1.4 条件语句和循环语句1.5 如何运用Array和Vector1.6 指针带来弹性1.7 文件的读写 前言 通过Essential C笔记的形式对C相关重点知识进行汇总,读者通读此系列文章就可以轻松的把该语言基础捡…...
07 Qt自绘组件:图片预览小组件ImageViewer
系列文章目录 01 Qt自定义风格控件的基本原则-CSDN博客 02 从QLabel聊起:自定义控件扩展-图片控件-CSDN博客 03 从QLabel聊起:自定义控件扩展-文本控件-CSDN博客 04 自定义Button组件:令人抓狂的QToolButton文本图标居中问题-CSDN博客 0…...

Groovy(第九节) Groovy 之单元测试
JUnit 利用 Java 对 Song 类进行单元测试 默认情况下 Groovy 编译的类属性是私有的,所以不能直接在 Java 中访问它们,必须像下面这样使用 setter: 编写这个测试用例余下的代码就是小菜一碟了。测试用例很好地演示了这样一点:用 Groovy 所做的一切都可以轻易地在 Java 程序…...

gprMax3.0随机介质建模
此处利用gprMax建立随机介质模型,采用matlab生成随机数组,保存为HDF5文件,此处为全代码,无需修改即可运行。在gprMax输入文件中使用#geometry_objects_read:读入自定义的随机模型 此文参考其他博主的自定义几何形状模块gprMax3.0建模时如何自定义目标的几何形状_#geomet…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

goreplay
1.github地址 https://github.com/buger/goreplay 2.简单介绍 GoReplay 是一个开源的网络监控工具,可以记录用户的实时流量并将其用于镜像、负载测试、监控和详细分析。 3.出现背景 随着应用程序的增长,测试它所需的工作量也会呈指数级增长。GoRepl…...
