【LeetCode-300】最长递增子序列(动归)
目录
题目描述
解法1:动态规划
代码实现
题目链接
题目描述
给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。
子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。
示例 1:
-
输入:nums = [10,9,2,5,3,7,101,18]
-
输出:4
-
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
示例 2:
-
输入:nums = [0,1,0,3,2,3]
-
输出:4
示例 3:
-
输入:nums = [7,7,7,7,7,7,7]
-
输出:1
提示:
-
1 <= nums.length <= 2500
-
-10^4 <= nums[i] <= 104
解法1:动态规划
这里我们可以使用dp数组,dp[i]表示了以数组nums[i]结尾的递增子序列。
-
dp[i]的定义
dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度,包括了自身,所以dp[0] = 1
为什么一定表示 “以nums[i]结尾的最长递增子序” ,因为我们在 做 递增比较的时候,如果比较 nums[j] 和 nums[i] 的大小,那么两个递增子序列一定分别以nums[j]为结尾 和 nums[i]为结尾, 要不然这个比较就没有意义了,不是尾部元素的比较那么 如何算递增呢。
-
状态转移方程
位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。
所以:if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
注意这里不是要dp[i] 与 dp[j] + 1进行比较,而是我们要取dp[j] + 1的最大值。
-
dp[i]的初始化
每一个i,对应的dp[i](即最长递增子序列)起始大小至少都是1.
-
确定遍历顺序
dp[i] 是有0到i-1各个位置的最长递增子序列 推导而来,那么遍历i一定是从前向后遍历。
j其实就是遍历0到i-1,那么是从前到后,还是从后到前遍历都无所谓,只要吧 0 到 i-1 的元素都遍历了就行了。 所以默认习惯 从前向后遍历。
遍历i的循环在外层,遍历j则在内层,代码如下:
for (int i = 1; i < nums.size(); i++) {for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);}if (dp[i] > result) result = dp[i]; // 取长的子序列
}代码实现
public class L300 {public int lengthOfLIS(int[] nums) {int len = nums.length;if (len == 1) return 1;int[] dp = new int[len];dp[0] = 1;for (int i = 1; i < len; i++) {for (int j = 0; j < i; j++) {if (nums[i]>nums[j]) {dp[i] = Math.max(dp[i], dp[j]);}}dp[i]++;}
return dp[len-1];}
}相关文章:
)
【LeetCode-300】最长递增子序列(动归)
目录 题目描述 解法1:动态规划 代码实现 题目链接 题目描述 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例…...
Mysterious-GIF-攻防世界-MISC
题目简介: 下载得到gif文件,十六进制编辑器查看,发现末尾有50 4B 03 04文件头。提取后保存为zip文件。 解压该zip文件,得到temp.zip。十六进制编辑器查看temp.zip,会发现有多个文件头和文件尾。 用binwalk分离temp.zi…...
【数据结构和算法初阶(C语言)】链表-单链表(手撕详讲单链表增删查改)
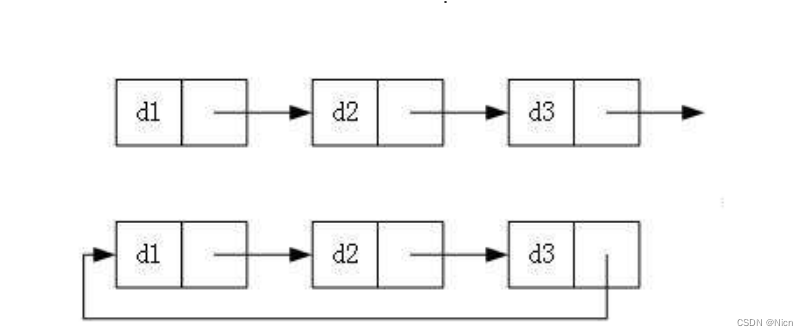
目录 1.前言:顺序表回顾: 1.1顺序表的优缺点 2.主角----链表 2.1链表的概念 2.2定义一个单链表的具体实现代码方式 3.单链表对数据的管理----增删查改 3.1单链表的创建 3.2单链表的遍历实现 3.2.1利用遍历实现一个打印我们链表内容的函数的函数…...
【Go语言】Go语言中的切片
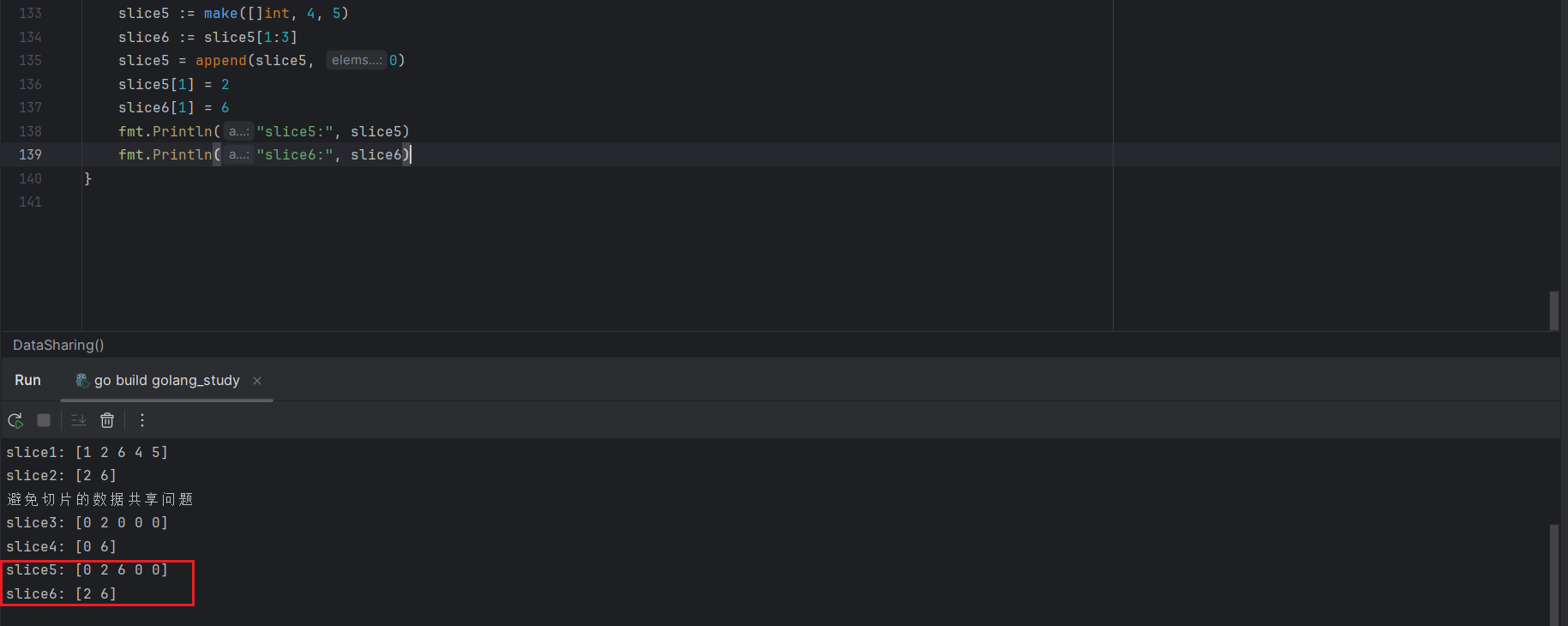
Go语言中的切片 1.切片的定义 Go语言中,切片是一个新的数据类型数据类型,与数组最大的区别在于,切片的类型中只有数据元素的类型,而没有长度: var slice []string []string{"a", "b", "c…...
Qt程序设计-钟表自定义控件实例
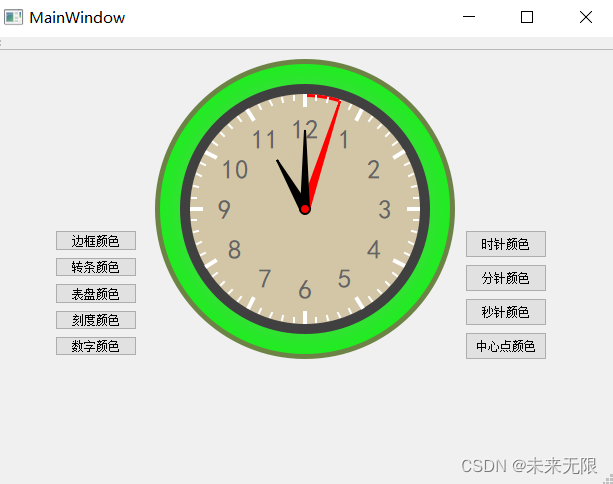
本文讲解Qt钟表自定义控件实例。 效果如下: 创建钟表类 #ifndef TIMEPIECE_H #define TIMEPIECE_H#include <QWidget> #include <QPropertyAnimation> #include <QDebug> #include <QPainter> #include <QtMath>#include <QTimer>#incl…...

Redis的发布订阅功能教程,实现实时消息和key过期事件通知功能
Redis的发布订阅 Redis的发布/订阅(Pub/Sub)功能是一种消息传递模式,用于实现消息发布者(publisher)和订阅者(subscriber)之间的消息通信。在这种模式下,消息的发送者(发布者)将消息发送到特定的频道(channel),而订阅了该频道的接收者(订阅者)将会接收到这些消息…...
4核8g服务器能支持多少人访问?
腾讯云4核8G服务器支持多少人在线访问?支持25人同时访问。实际上程序效率不同支持人数在线人数不同,公网带宽也是影响4核8G服务器并发数的一大因素,假设公网带宽太小,流量直接卡在入口,4核8G配置的CPU内存也会造成计算…...

【Android】切换系统全局语言设置
前两种为应用内部处理,第三种为发送广播由系统服务进行处理 使用反射 这种会直接将安卓设置内的语言列表清空,然后将选择的语言设置为系统语言 该方法存在问题,在首次开机后设置会导致国外应用进不去(只对于here地图个别版本) /*** 设置语言…...
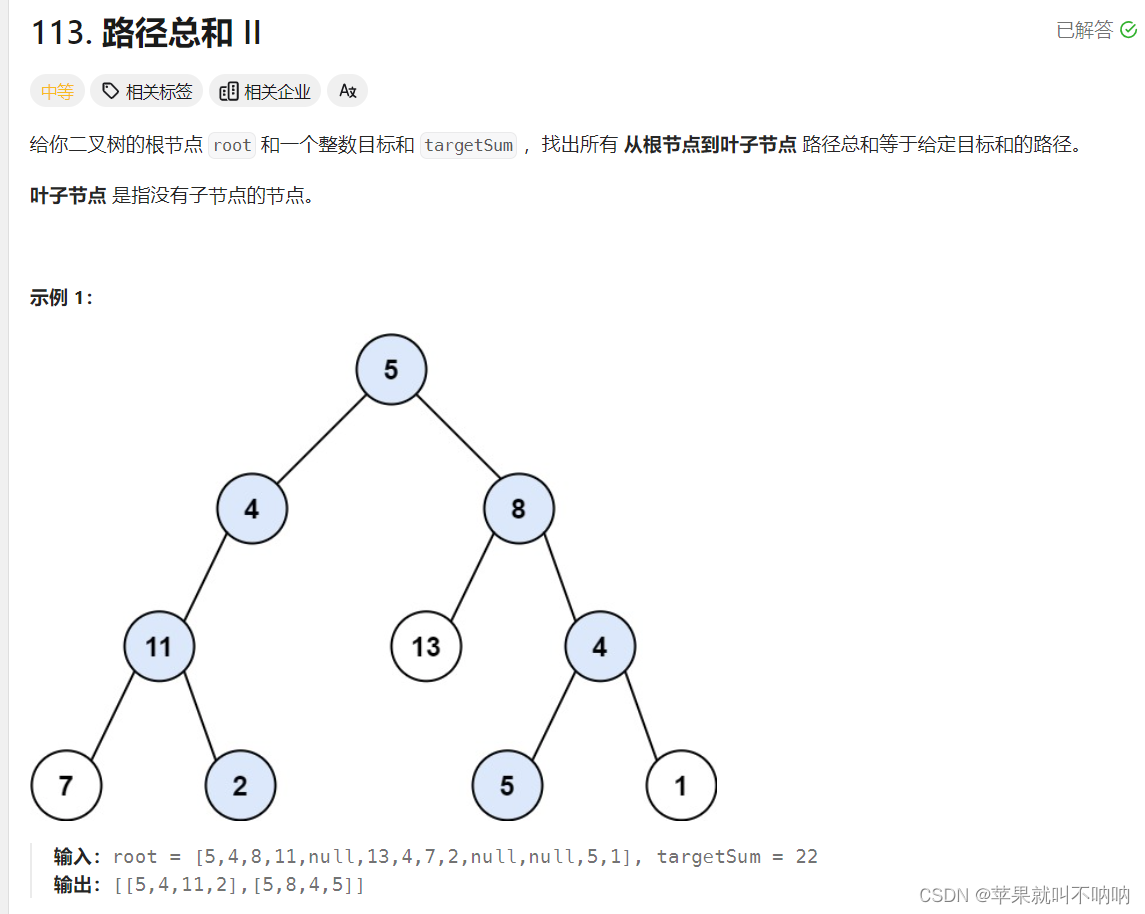
【递归】【回溯】Leetcode 112. 路径总和 113. 路径总和 II
【递归】【回溯】Leetcode 112. 路径总和 113. 路径总和 II 112. 路径总和解法:递归 有递归就有回溯 记得return正确的返回上去 113. 路径总和 II解法 递归 如果需要搜索整棵二叉树,那么递归函数就不要返回值 如果要搜索其中一条符合条件的路径ÿ…...
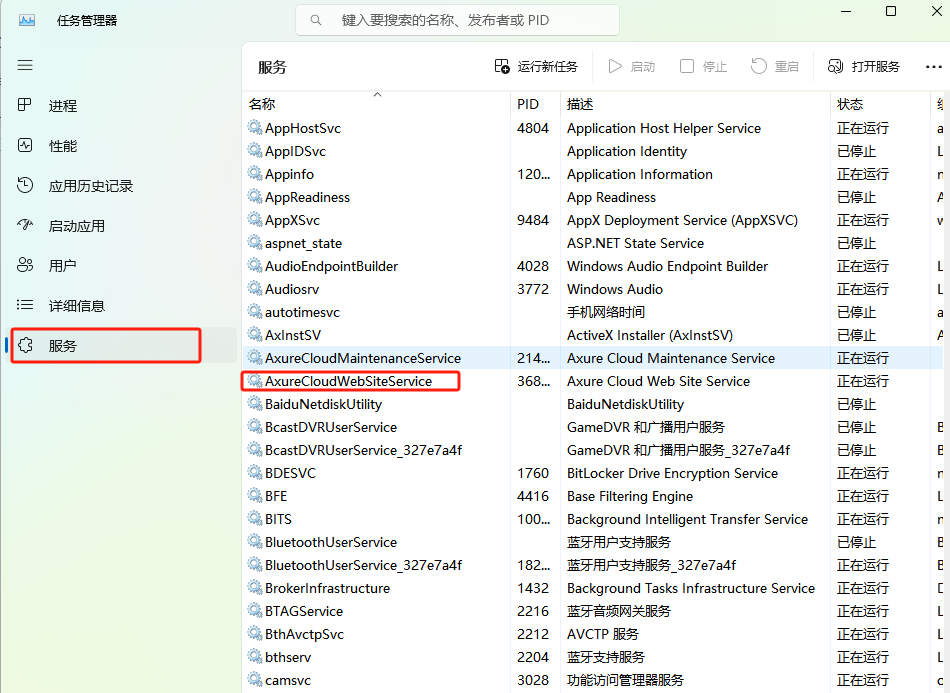
AxureCloud配置文件详细介绍
AxureCloud配置文件详细介绍 原文地址:https://docs.axure.com/axure-cloud/business/custom-settings-json/ 通过修改 customsettings.json 可以修改AxureCloud私有部署的域名、端口、HTTPS、存储目录、是否开启插件等, 默认安装的路径为: C:\Program Files\Axure…...

Centos开机网卡自启动失败
问题背景 每次都要手动启动在这里插入代码片 解决方案: 关闭 NetworkManager 服务 systemctl disable NetworkManager systemctl stop NetworkManager重启就会发现网卡已经可以自动启动了...
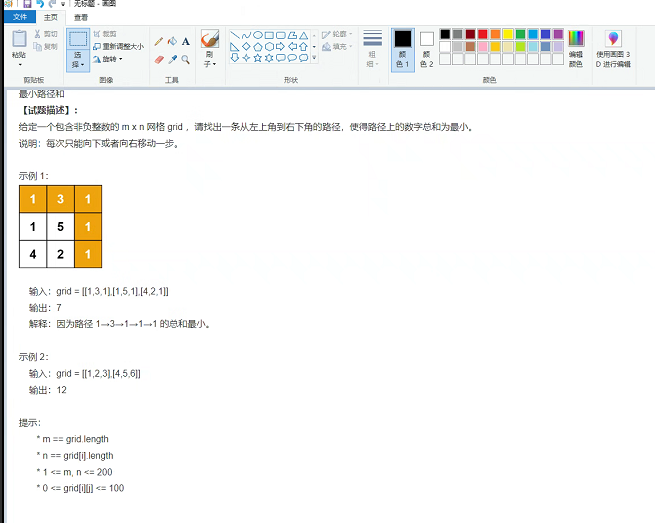
华为OD技术面试案例3-2024年
技术一面: 1.手撕代码,算法题: 【最小路径和】 手撕代码通过,面试官拍了照片 2.深挖项目,做过的自认为最好的一个项目,描述做过的项目的工作过程,使用到哪些技术? 技术二面&…...

全面升级!Apache HugeGraph 1.2.0版本发布
图数据库以独特的数据管理和分析能力,在企业数智化转型的过程中正在成为数据治理的核心,根据IDC调研显示,95%的企业认为图数据库是重要的数据管理工具,超过65%的厂商认为在业务上图数据库优于其他选择,尤其是在金融风控…...

WinCC如何与三菱Q系列PLC进行以太网通讯
本文主要描述人机界面WinCC如何与三菱Q系列PLC进行以太网通讯,主要介绍了CPU自带以太网口和扩展以太网模块两种情况以及分别使用TCP、UDP两种协议进行通讯组态步骤及其注意事项。 一、 说明 WinCC从V7.0 SP2版本开始增加了三菱以太网驱动程序,支持和三…...
Spring11、整合Mybatis
11、整合Mybatis 步骤: 导入相关jar包 junit <dependency><groupId>junit</groupId><artifactId>junit</artifactId><version>4.12</version> </dependency> mybatis <dependency><groupId>org.my…...
错误的集合)
C语言练习:(力扣645)错误的集合
题目链接:645. 错误的集合 - 力扣(LeetCode) 集合 s 包含从 1 到 n 的整数。不幸的是,因为数据错误,导致集合里面某一个数字复制了成了集合里面的另外一个数字的值,导致集合 丢失了一个数字 并且 有一个数字…...

广和通发布基于MediaTek T300平台的RedCap模组FM330系列及解决方案
世界移动通信大会MWC 2024期间,广和通发布基于MediaTek T300平台的RedCap模组FM330系列,加速5G-A繁荣发展。FM330系列及其解决方案采用全球先进RedCap方案,满足移动宽带和工业互联对高能效的需求。 广和通FM330系列采用全球首款6nm制程且集成…...

代码随想录训练营第六十三天打卡|503.下一个更大元素II 42. 接雨水
503.下一个更大元素II 1.暴力法,和每日温度那一题如出一辙,循环数组用了一个取模运算就解决了。 class Solution { public:vector<int> nextGreaterElements(vector<int>& nums) {int n nums.size();vector<int> result;for (i…...
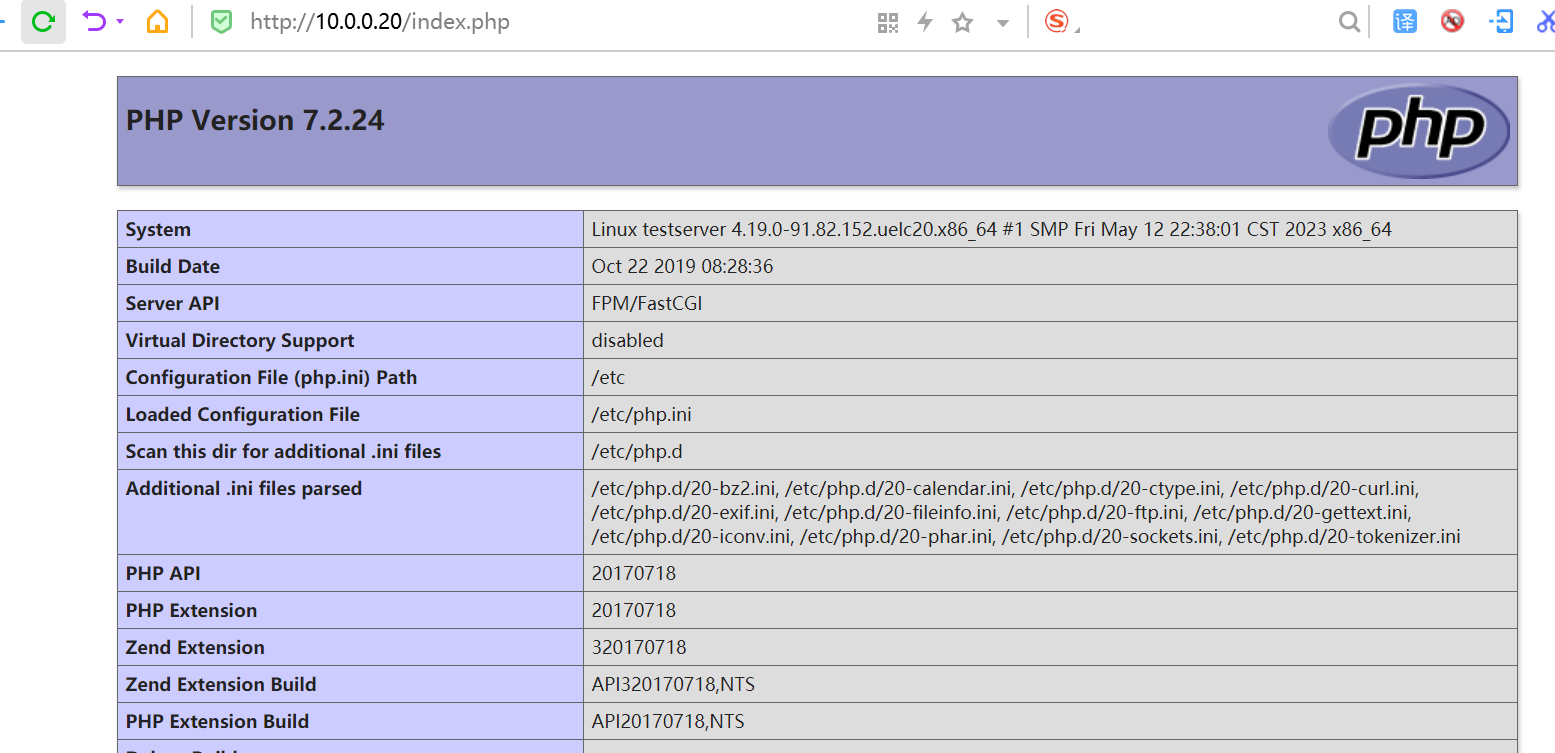
【web】nginx+php环境搭建-关键点(简版)
一、nginx和php常用命令 命令功能Nginxphp-fpm启动systemctl start nginxsystemctl start php-fpm停止systemctl stop nginxsystemctl stop php-fpm重启systemctl restart nginxsystemctl restart php-fpm查看启动状态systemctl status nginxsystemctl status php-fpm开机自启…...

1、什么是ETF?
ETF是Exchange Traded Fund的英文缩写,中文称为“交易型开放式指数基金”,又称“指数股”。ETF是一种指数投资工具,通过复制标的指数来构建跟踪指数变化的组合证券,使得投资者通过买卖一种产品就实现了一揽子证券的交易。简单来说…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

Canal环境搭建并实现和ES数据同步
作者:田超凡 日期:2025年6月7日 Canal安装,启动端口11111、8082: 安装canal-deployer服务端: https://github.com/alibaba/canal/releases/1.1.7/canal.deployer-1.1.7.tar.gz cd /opt/homebrew/etc mkdir canal…...
