【Day59】代码随想录之动态规划_647回文子串_516最长回文子序列
文章目录
- 动态规划理论基础
- 动规五部曲:
- 出现结果不正确:
- 1. 647回文子串
- 2. 516最长回文子序列
动态规划理论基础
动规五部曲:
- 确定dp数组 下标及dp[i] 的含义。
- 递推公式:比如斐波那契数列 dp[i] = dp[i-1] + dp[i-2]。
- 初始化dp数组。
- 确定遍历顺序:从前到后or其他。
- 打印。
出现结果不正确:
- 打印dp日志和自己想的一样:递推公式、初始化或者遍历顺序出错。
- 打印dp日志和自己想的不一样:代码实现细节出现问题。
1. 647回文子串
参考文档:代码随想录
分析:
判断一个字符串里面的有多少个回文串,需要二维dp数组,dp[i][j]表示字符串s的[i, j]之间有多少个回文字符串。当s[i] == s[j]的时候,有可能是回文串,i = j 或者 i和j相差一个时是回文串,如果i和j相差的大于1,则需要判断[i+1, j-1]是否是回文串了。而当s[i] != s[j]的时候,s的[i, j]肯定不是回文串,这也表示dp的初始化是false。
dp五部曲:
- dp[i][j]含义:表示s[i, j]回文串的个数。统计一个字符串中回文串的个数,使用的是bool型的数组,如果dp[i][j] = true;那么最终的回文串个数加1,而不是记录有多少个回文子串。数组类型的设计也很有意思。
- 递推公式:if(s[i] == s[j]) { if(j - i <= 1) {dp[i][j] = true; } else { dp[i][j] = dp[i+1][j-1]; } }
- 初始化:dp[i][j] = false;
- 遍历顺序:根据递推公式可以得知当前的dp[i][j]有可能需要借助左下方的dp[i+1][j-1],所以遍历顺序是从下到上,先更新下面一行的数据;之后从左到右,先更新左侧的数据。
代码:
class Solution {
public:int countSubstrings(string s) {//dp[i]: 以i结尾的回文子串的个数tvector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));int sum = 0;//注意遍历的顺序是从下到上,从左到右的for(int i = s.size() - 1; i >= 0; i--){for(int j = i; j < s.size(); j++){if(s[i] == s[j]) {if(j - i <= 1) {dp[i][j] = true;sum++;}else if(dp[i+1][j-1]){dp[i][j] = true;sum++;}}}}return sum;}
};
2. 516最长回文子序列
参考文档:代码随想录
分析:
和上一题回文子串不同的地方在于这次的回文子序列不要求是连续的。所以还采用和上一题一样的方法使用二维的dp数组。但是为了更新回文子串的长度,需要将数组的类型设为int型。
dp五部曲:
- dp[i][j]含义:表示字符串s中[i, j]之间的最长回文子序列。
- 递推公式:if(s[i] == s[j]) dp[i][j] = dp[i+1][j-1] + 2; else dp[i][j] = max(dp[i+1][j], dp[i][j-1]);

- 初始化:dp[i][i] = 1。其余为0。
- 遍历顺序:根据递推公式,遍历顺序是从下到上,先把下一行的数据更新好,根据下一行的数据更新本行的数据;从左到右,先更新左侧的数据,根据左侧的数据更新本位置的数据。

代码:
class Solution {
public:int longestPalindromeSubseq(string s) {//返回最长回文串的长度,数组类型是int型vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));//初始化for(int i = 0; i < s.size(); i++) dp[i][i] = 1;//更新dpfor(int i = s.size() - 1; i >= 0; i--){for(int j = i + 1; j < s.size(); j++){if(s[i] == s[j]) dp[i][j] = dp[i+1][j-1] + 2;else{dp[i][j] = max(dp[i+1][j], dp[i][j-1]);}}}return dp[0][s.size() - 1];}
};
相关文章:

【Day59】代码随想录之动态规划_647回文子串_516最长回文子序列
文章目录 动态规划理论基础动规五部曲:出现结果不正确: 1. 647回文子串2. 516最长回文子序列 动态规划理论基础 动规五部曲: 确定dp数组 下标及dp[i] 的含义。递推公式:比如斐波那契数列 dp[i] dp[i-1] dp[i-2]。初始化dp数组…...
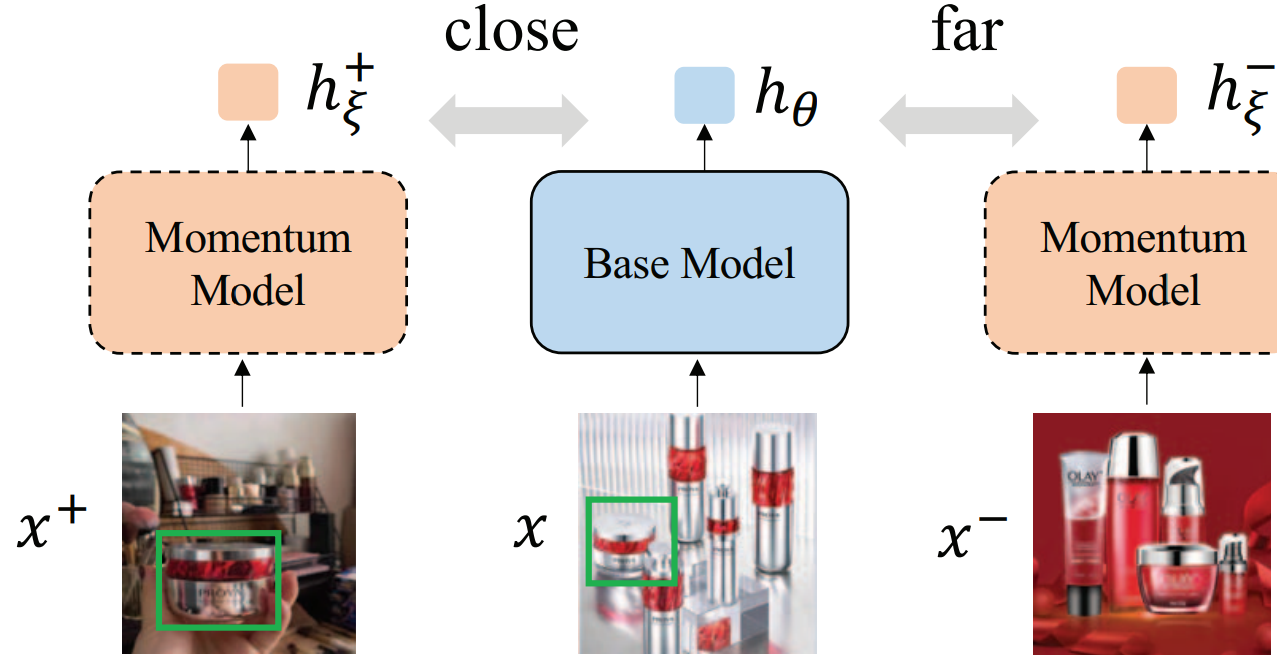
ECLIP
denote the representation of the positive prompt produced by the momentum model as h ξ i h_{\xi}^{i} hξi 辅助信息 作者未提供代码...
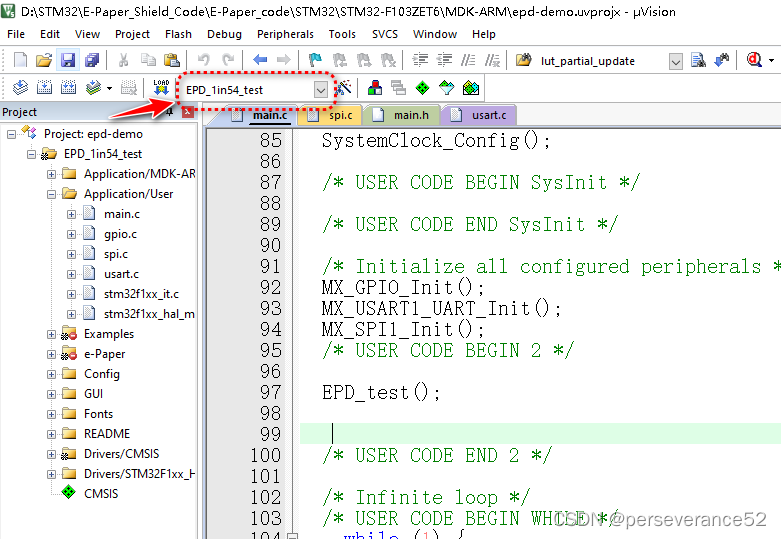
STM32 +合宙1.54“ 电子墨水屏(e-paper)驱动显示示例
STM32 合宙1.54“ 电子墨水屏(e-paper)驱动显示示例 📍相关篇《Arduino框架下ESP32/ESP8266合宙1.54“ 电子墨水屏(e-paper)驱动显示示例》🔖程序是从GooDisplay品牌和微雪电子下同型号规格墨水屏的示例程序…...
使用Postman和JMeter进行signature签名
一、前言 有些接口的请求会带上sign(签名)进行请求,各接口对sign的签名内容、方式可能不一样,但一般都是从接口的入参中选择部分内容组成一个字符串,然后再进行签名操作, 将结果赋值给sign; 完整规范的接口文档都会…...
uni-app nvue vue3 setup中实现加载webview,解决nvue中获取不到webview实例的问题
注意下面的方法只能在app端使用, let wv plus.webview.create("","custom-webview",{plusrequire:"none", uni-app: none, width: 300,height:400,top:uni.getSystemInfoSync().statusBarHeight44 }) wv.loadURL("https://ww…...

IPD(集成产品开发)—核心思想
企业发展到一定阶段就会遇到管理瓶颈,IPD流程是一种高度结构化的产品开发流程,它集成了业界很多优秀的产品开发方法论,像搭积木一样的组合成一种非常有效的流程。如果我们能根据企业的规模和行业特点,对全流程的IPD进行合适的裁剪…...

uniapp android 原生插件开发-测试流程
前言 最近公司要求研究一下 uniapp 的 android 原生插件的开发,为以后的工作做准备。这篇文章记录一下自己的学习过程,也帮助一下有同样需求的同学们 : ) 一、下载安装Hbuilder X , Android studio(相关的安装配置过程网上有很多,…...
)
MyCAT从入门到实战(配置文件介绍)
用户(user) 配置文件位置mycat/conf/user/root.user.json。这个配置文件主要是用来配置MyCAT的登录用户 的,也就是我们连接8066这个端口的用户信息。 [rootservice bin]# cat /usr/local/mycat/conf/users/root.user.json {"dialect&q…...
)
【LeetCode-300】最长递增子序列(动归)
目录 题目描述 解法1:动态规划 代码实现 题目链接 题目描述 给你一个整数数组 nums ,找到其中最长严格递增子序列的长度。 子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例…...
Mysterious-GIF-攻防世界-MISC
题目简介: 下载得到gif文件,十六进制编辑器查看,发现末尾有50 4B 03 04文件头。提取后保存为zip文件。 解压该zip文件,得到temp.zip。十六进制编辑器查看temp.zip,会发现有多个文件头和文件尾。 用binwalk分离temp.zi…...
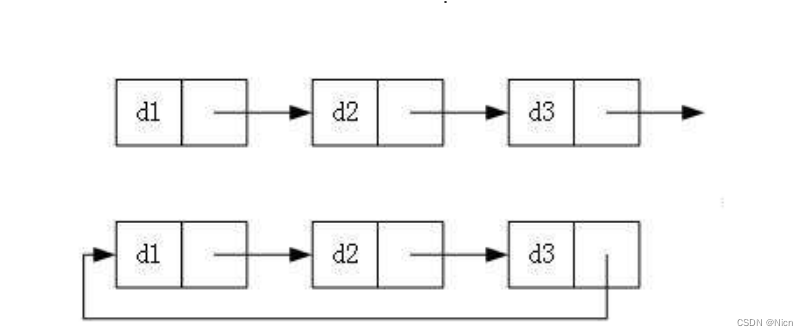
【数据结构和算法初阶(C语言)】链表-单链表(手撕详讲单链表增删查改)
目录 1.前言:顺序表回顾: 1.1顺序表的优缺点 2.主角----链表 2.1链表的概念 2.2定义一个单链表的具体实现代码方式 3.单链表对数据的管理----增删查改 3.1单链表的创建 3.2单链表的遍历实现 3.2.1利用遍历实现一个打印我们链表内容的函数的函数…...
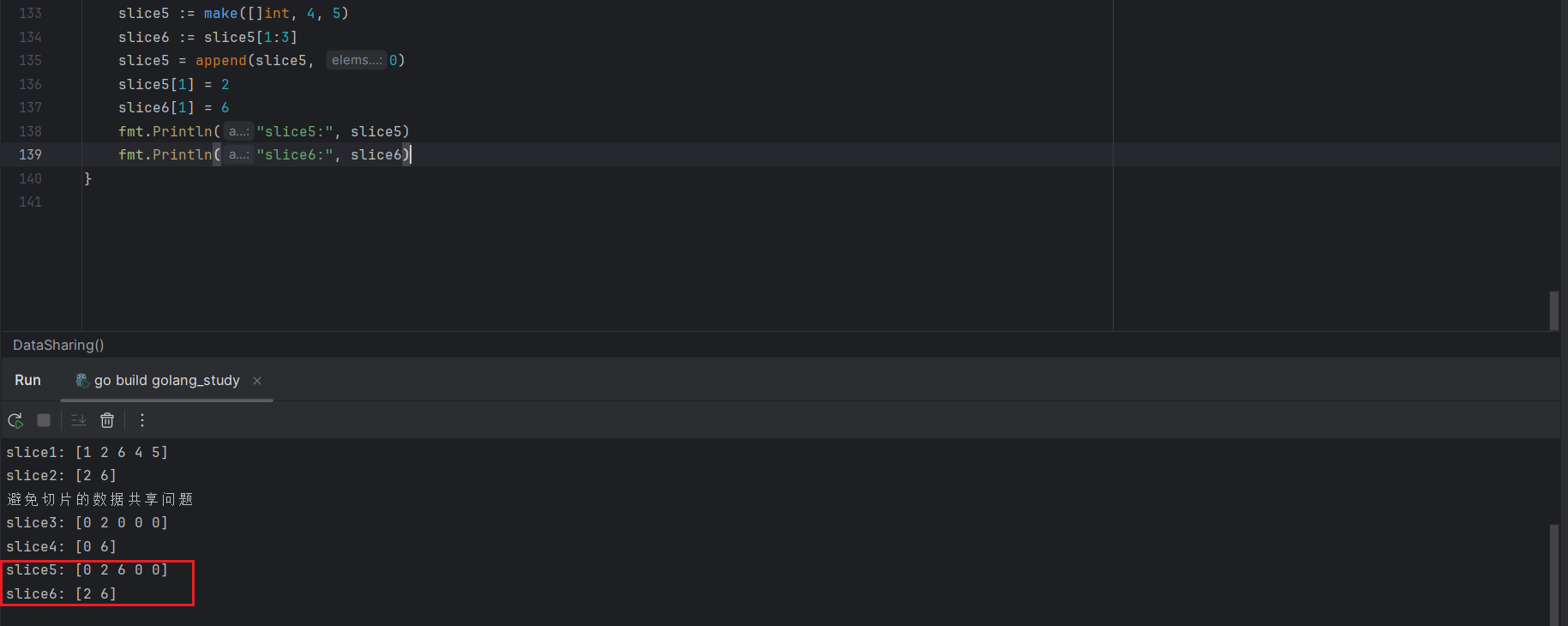
【Go语言】Go语言中的切片
Go语言中的切片 1.切片的定义 Go语言中,切片是一个新的数据类型数据类型,与数组最大的区别在于,切片的类型中只有数据元素的类型,而没有长度: var slice []string []string{"a", "b", "c…...
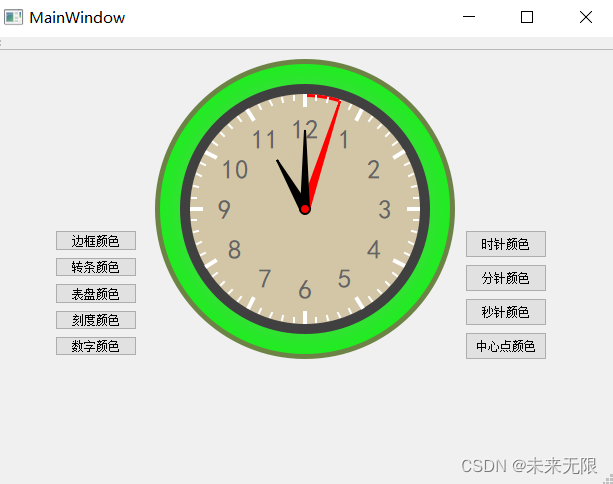
Qt程序设计-钟表自定义控件实例
本文讲解Qt钟表自定义控件实例。 效果如下: 创建钟表类 #ifndef TIMEPIECE_H #define TIMEPIECE_H#include <QWidget> #include <QPropertyAnimation> #include <QDebug> #include <QPainter> #include <QtMath>#include <QTimer>#incl…...

Redis的发布订阅功能教程,实现实时消息和key过期事件通知功能
Redis的发布订阅 Redis的发布/订阅(Pub/Sub)功能是一种消息传递模式,用于实现消息发布者(publisher)和订阅者(subscriber)之间的消息通信。在这种模式下,消息的发送者(发布者)将消息发送到特定的频道(channel),而订阅了该频道的接收者(订阅者)将会接收到这些消息…...
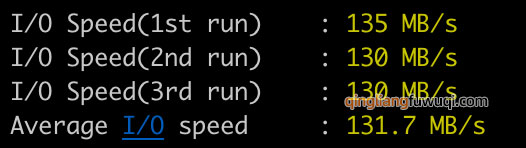
4核8g服务器能支持多少人访问?
腾讯云4核8G服务器支持多少人在线访问?支持25人同时访问。实际上程序效率不同支持人数在线人数不同,公网带宽也是影响4核8G服务器并发数的一大因素,假设公网带宽太小,流量直接卡在入口,4核8G配置的CPU内存也会造成计算…...

【Android】切换系统全局语言设置
前两种为应用内部处理,第三种为发送广播由系统服务进行处理 使用反射 这种会直接将安卓设置内的语言列表清空,然后将选择的语言设置为系统语言 该方法存在问题,在首次开机后设置会导致国外应用进不去(只对于here地图个别版本) /*** 设置语言…...
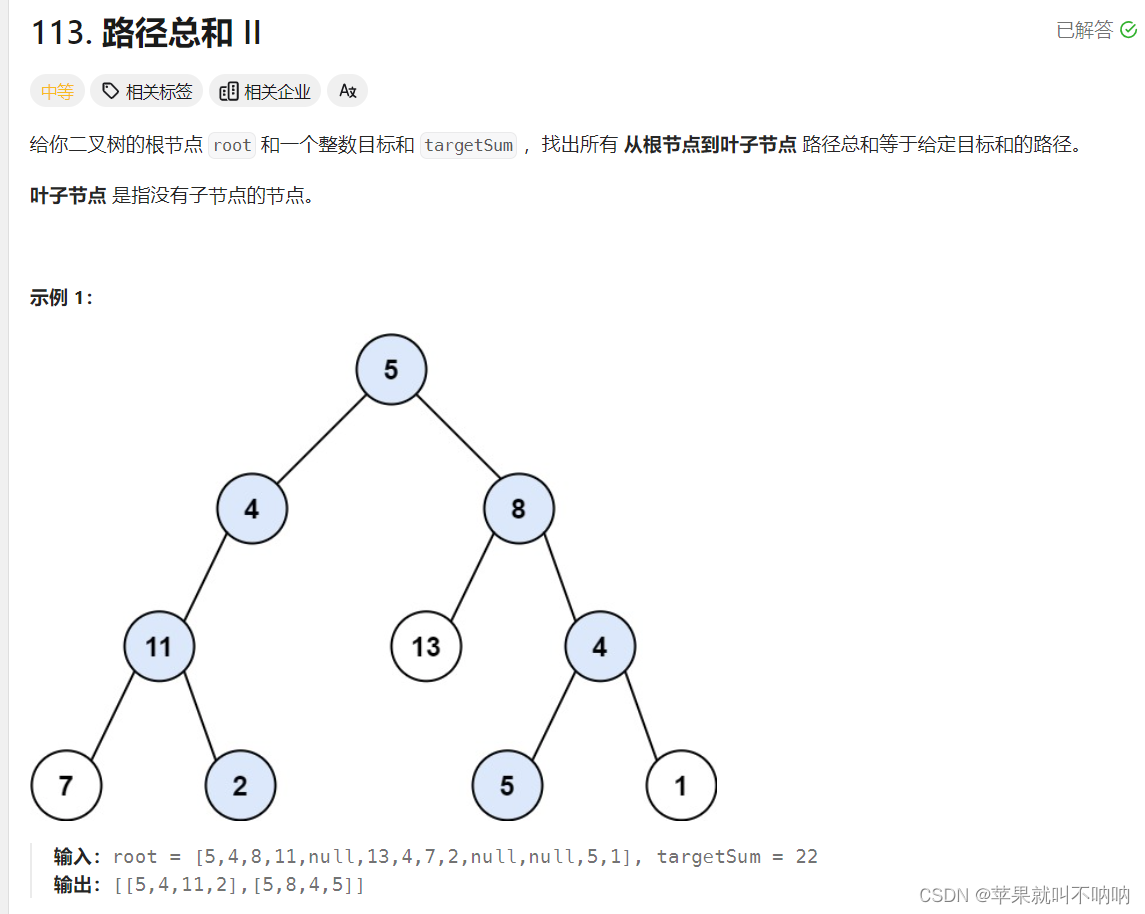
【递归】【回溯】Leetcode 112. 路径总和 113. 路径总和 II
【递归】【回溯】Leetcode 112. 路径总和 113. 路径总和 II 112. 路径总和解法:递归 有递归就有回溯 记得return正确的返回上去 113. 路径总和 II解法 递归 如果需要搜索整棵二叉树,那么递归函数就不要返回值 如果要搜索其中一条符合条件的路径ÿ…...
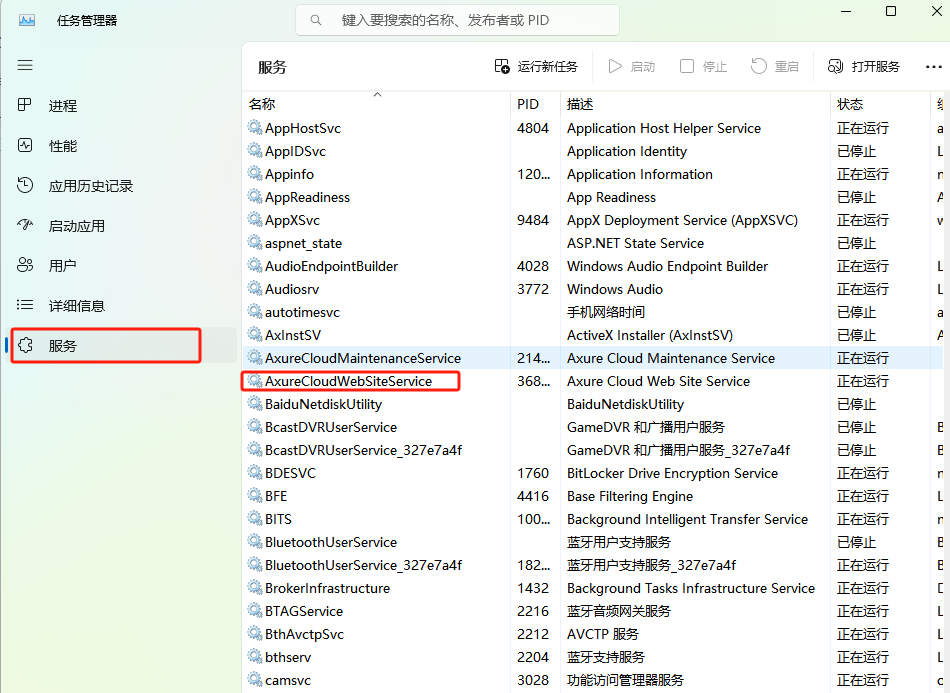
AxureCloud配置文件详细介绍
AxureCloud配置文件详细介绍 原文地址:https://docs.axure.com/axure-cloud/business/custom-settings-json/ 通过修改 customsettings.json 可以修改AxureCloud私有部署的域名、端口、HTTPS、存储目录、是否开启插件等, 默认安装的路径为: C:\Program Files\Axure…...

Centos开机网卡自启动失败
问题背景 每次都要手动启动在这里插入代码片 解决方案: 关闭 NetworkManager 服务 systemctl disable NetworkManager systemctl stop NetworkManager重启就会发现网卡已经可以自动启动了...
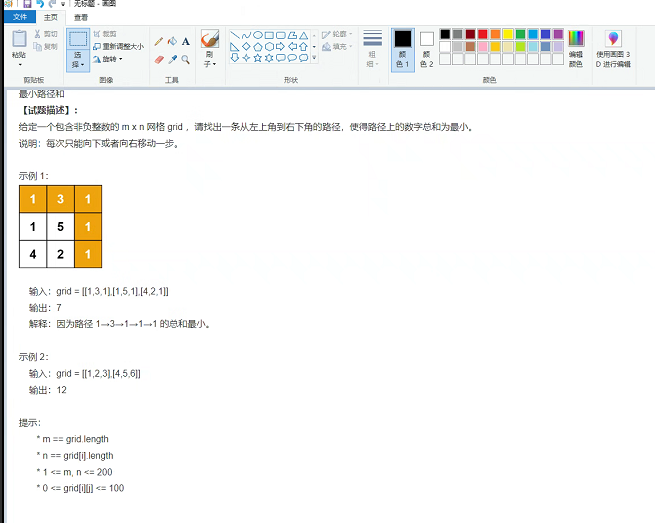
华为OD技术面试案例3-2024年
技术一面: 1.手撕代码,算法题: 【最小路径和】 手撕代码通过,面试官拍了照片 2.深挖项目,做过的自认为最好的一个项目,描述做过的项目的工作过程,使用到哪些技术? 技术二面&…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

USB Over IP专用硬件的5个特点
USB over IP技术通过将USB协议数据封装在标准TCP/IP网络数据包中,从根本上改变了USB连接。这允许客户端通过局域网或广域网远程访问和控制物理连接到服务器的USB设备(如专用硬件设备),从而消除了直接物理连接的需要。USB over IP的…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...
