大语言模型LLM分布式训练:大规模数据集上的并行技术全景探索(LLM系列03)
文章目录
- 大语言模型LLM分布式训练:大规模数据集上的并行技术全景探索(LLM系列03)
- 1. 引言
- 1.1 大语言模型(LLM)的重要性及其规模化挑战
- 1.2 分布式训练策略的需求
- 2. 分布式训练基础原理
- 2.1 并行计算的基本概念与分类
- 3. LLM分布式训练的关键技术
- 3.1 分布式同步训练算法
- 3.2 参数服务器架构
- 3.3 异步训练与优化策略
- 3.4 超大规模LLM中的通信开销与梯度一致性解决方案
大语言模型LLM分布式训练:大规模数据集上的并行技术全景探索(LLM系列03)
1. 引言
1.1 大语言模型(LLM)的重要性及其规模化挑战
大语言模型,如GPT-3、BERT等,在自然语言处理(NLP)领域取得了革命性的突破,其强大的泛化能力、丰富的语义理解和生成能力对AI发展至关重要。然而,随着模型参数量的增长和所需处理的训练数据规模剧增,传统的单机训练方式已无法满足需求。一方面,训练时间显著增加;另一方面,硬件资源限制了模型的进一步扩展。因此,寻求有效的分布式训练策略成为了解决这一挑战的关键。
1.2 分布式训练策略的需求
分布式训练通过将计算任务分散到多个节点上执行,以提高训练效率,缩短收敛时间,并实现更大规模模型的训练。这种策略可以充分利用集群资源,解决单一设备内存和计算力不足的问题,从而推动LLM向更深、更广的方向发展。
2. 分布式训练基础原理
2.1 并行计算的基本概念与分类
并行计算是指同时使用多个处理器或计算机来协同解决问题的过程。在LLM分布式训练中,主要采用三种并行模式:
-
数据并行:将大型数据集划分为多个子集(批次),每个计算节点独立地处理一个子集的数据,然后汇总更新全局模型参数。
# 示例代码简化版 - 假设我们正在使用PyTorch进行数据并行 import torch.nn.parallel model = MyLanguageModel() data_loader = get_data_loader(batch_size=BATCH_SIZE, num_workers=NUM_WORKERS)device = 'cuda' if torch.cuda.is_available() else 'cpu' model.to(device) model = torch.nn.DataParallel(model, device_ids=list(range(NUM_GPUS))) # 使用多GPU进行数据并行for batch in data_loader:inputs, targets = batchinputs, targets = inputs.to(device), targets.to(device)output = model(inputs)# ... 计算损失并反向传播 ... -
模型并行:将模型结构按层或单元分割成多个部分,分别分配给不同设备并行计算,每个设备仅负责模型的一部分。
-
流水线并行:在模型层级结构上实施并行,将模型的不同层分解到不同的计算单元,形成一个连续的处理管线,每一步都在各自的设备上按顺序执行,减少等待时间。
3. LLM分布式训练的关键技术
3.1 分布式同步训练算法
同步训练算法如All-Reduce是确保各计算节点间梯度同步的重要手段。所有节点计算出本地梯度后,通过高效的通信协议(例如Ring All-Reduce)汇总所有节点的梯度信息,然后统一更新模型参数。
3.2 参数服务器架构
Parameter Server是一种常用的分布式系统设计模式,它作为中心化的存储和协调器,负责维护和更新模型参数。各个计算节点异步地从参数服务器读取参数,计算局部梯度,再将梯度发送回参数服务器进行更新。
3.3 异步训练与优化策略
异步训练允许不同节点根据自己的进度更新全局模型,但可能导致不稳定的收敛性和一致性问题。实践中,研究者尝试通过控制更新频率、优化通信策略以及使用延迟补偿等方法平衡效率与稳定性。
3.4 超大规模LLM中的通信开销与梯度一致性解决方案
为降低通信开销,可采取梯度压缩、稀疏通信、选择性通信等策略。同时,为了保证梯度一致性,还引入了诸如同步屏障、动态调整学习率等算法和技术。
相关文章:
)
大语言模型LLM分布式训练:大规模数据集上的并行技术全景探索(LLM系列03)
文章目录 大语言模型LLM分布式训练:大规模数据集上的并行技术全景探索(LLM系列03)1. 引言1.1 大语言模型(LLM)的重要性及其规模化挑战1.2 分布式训练策略的需求 2. 分布式训练基础原理2.1 并行计算的基本概念与分类 3.…...

98.验证二叉搜索树
98.验证二叉搜索树 思路 1.一开始使用递归,想当前节点满足条件后,再使左右子树分别满足条件。失败,只考虑了节点与左右子树的大小,未考虑隔代节点的关系。 2.转变思路,使用中序遍历的方法,从第一个节点开…...

2月21日,每日信息差
🎖 素材来源官方媒体/网络新闻 🎄 10 家央企签订倡议书:将主动向社会开放人工智能应用场景 🌍 上海成为首个固定资产投资破万亿的一线城市 🌋 特斯拉扩建德国工厂的计划遭当地居民反对 🎁 加拿大公司利用木…...

android.text.BoringLayout.isBoring 的 NullPointerException
都是重写TextView.settext()函数导致的坑~ override fun setText(text: CharSequence?, type: BufferType?) {if (text.isNullOrEmpty()) {return}//业务代码super.setText(text, type)} java.lang.NullPointerException at android.text.BoringLayout.isBoring(BoringLayo…...
C++ 高频考点
1. C/C内存有哪几种类型? C中,内存分为5个区:堆(malloc)、栈(如局部变量、函数参数)、程序代码区(存放二进制代码)、全局/静态存储区(全局变量、static变量)和常量存储区(常量&…...
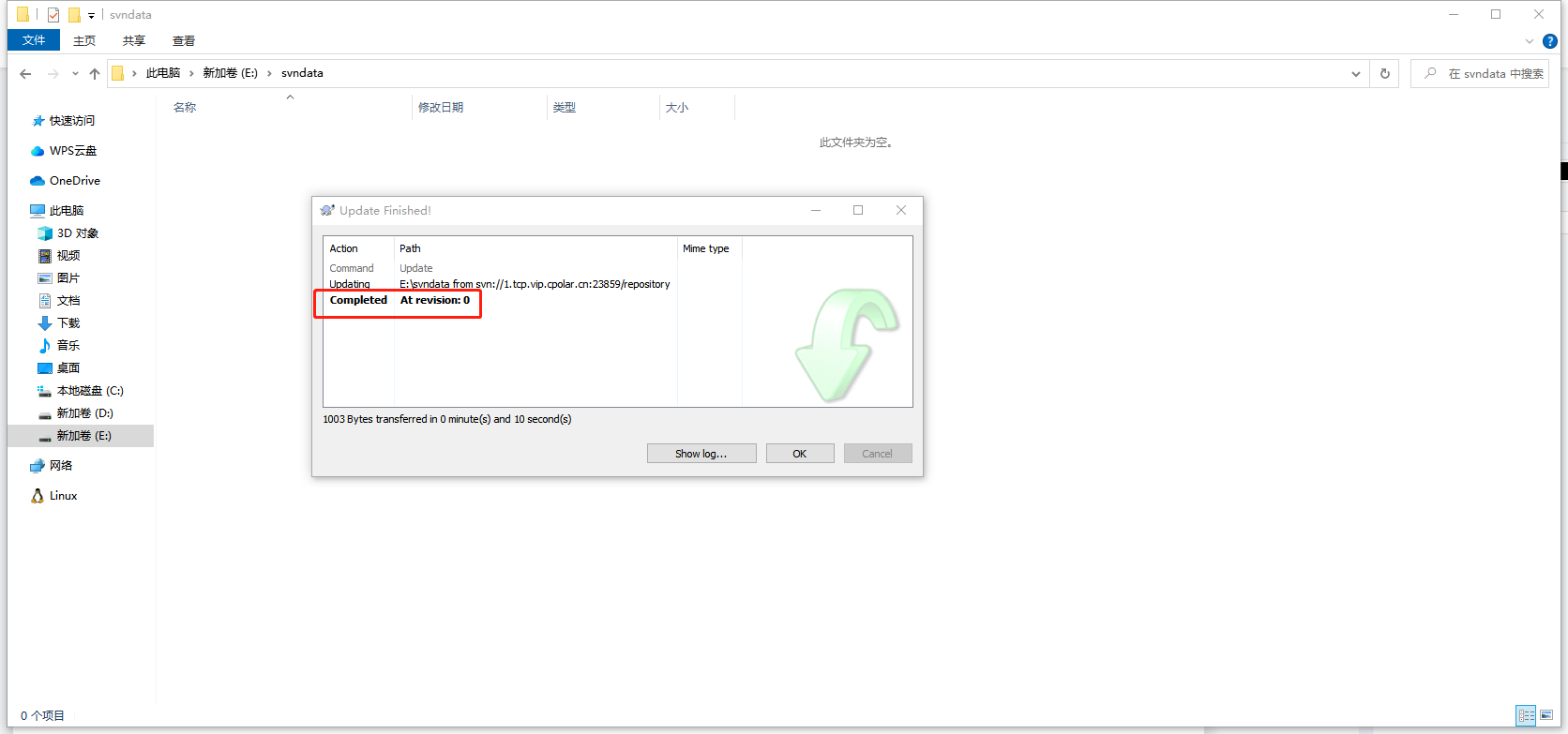
Ubuntu安装SVN服务并结合内网穿透实现公网访问本地存储文件
最近,我发现了一个超级强大的人工智能学习网站。它以通俗易懂的方式呈现复杂的概念,而且内容风趣幽默。我觉得它对大家可能会有所帮助,所以我在此分享。点击这里跳转到网站。 文章目录 前言1. Ubuntu安装SVN服务2. 修改配置文件2.1 修改svns…...

2月20日,每日信息差
第一、中国联通 1 月智慧客服客户问题解决率为 97.9%,大联接用户达 10.02 亿户,5G 套餐用户约 2.64 亿户,物联网终端连接约 5.06 亿户。5G 行业虚拟专网服务客户数为 9185 个,智慧客服问题解决率 97.9%,智能服务占比 8…...

Visual Studio清单作用
1、作用: 制定程序依赖的C运行库的dll及版本,包括mfc,atl,crt等,在Visual Studio安装目录下的vc/redist下有debug和release版本 2、确定应用程序依赖哪些visual C 库方法: 查看项目-》项目设置-》常规&…...
方法的区别是?hashCode()和equals()的关系是什么?)
Java中的==和equals()方法的区别是?hashCode()和equals()的关系是什么?
目录 解释Java中的和equals()方法。 hashCode()和equals()的关系是什么? 解释Java中的和equals()方法。 在Java中,和equals()方法都用于比较两个对象,但它们在比较时的侧重点和行为上有所不同。 1. **运算符:** - 是Java中的…...

yaml-cpp开源库使用
源码下载:https://github.com/jbeder/yaml-cpp 1.yaml-cpp编译 步骤主要如下:进入源码目录后 mkdir build cd build cmake … make make install 2.代码示例 #include "funset.hpp" #include <string> #include <fstream> #i…...

【C++私房菜】序列式容器的迭代器失效问题
目录 一、list的迭代器失效 二、vector的迭代器失效 1、空间缩小操作 2、空间扩大操作 三、总结 在C中,当对容器进行插入或删除操作时,可能会导致迭代器失效的问题。所谓迭代器失效指的是,原先指向容器中某个元素的迭代器,在…...
MySQL 篇-深入了解 DML、DQL 语言(二)
🔥博客主页: 【小扳_-CSDN博客】 ❤感谢大家点赞👍收藏⭐评论✍ 文章目录 1.0 DML、DQL 语言说明 2.0 使用 DML 实现对数据管理和操作 2.1 DML - 增添数据 insert 2.2 DML - 修改数据 update 2.3 DML - 删除数据 delete 3.0 使用 DQL 实现对…...
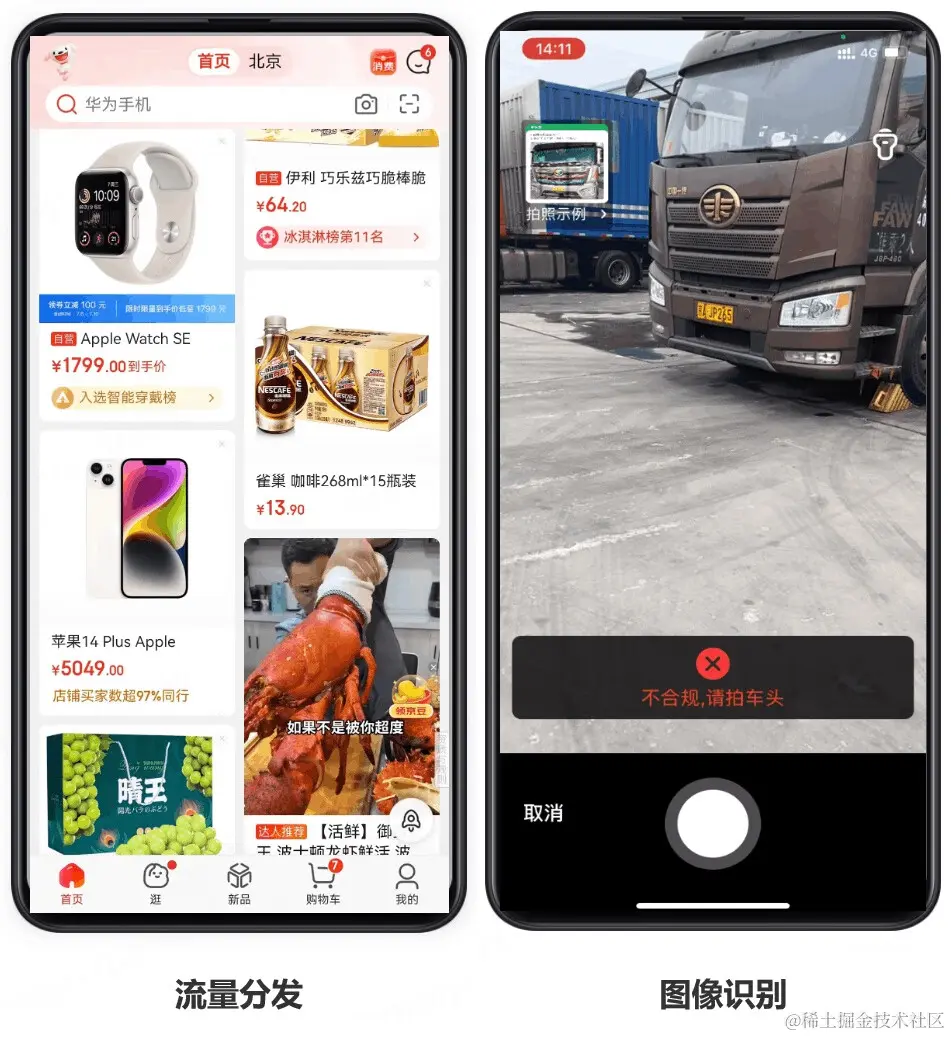
端智能:面向手机计算环境的端云协同AI技术创新
近年来,随着移动端设备软硬件能力的进步,移动端的算力有了很大提升,同时面向移动端的机器学习框架和模型轻量化技术越来越成熟,端上的AI能力逐渐进入大众视野,端智能在电商领域也开始逐步走向规模化应用。通过持续探索…...

PHP函数 “password_hash“ 哈希密码
哈希函数是一种将输入转换为固定长度字符串的方法,这个过程是不可逆的,也就是无法从哈希值还原出原始输入。通过将密码进行哈希处理,即使数据库泄露,攻击者也无法简单地获取到用户密码。 在PHP中,我们可以使用 "…...

第十一天-Excel的操作
目录 1.xlrd-Excel的读模块 安装 使用 获取工作簿 读取工作簿的内容 xlsxwriter-Excel的写模块 安装 使用 生成图表 add_series参数 图表的样式 demo:生成图表 Excel的操作在python中有多个模块,为了能够快速使用,选择了相对简单…...

【java任意文件漏洞修复,使用文件魔数解决】
java任意文件漏洞修复,使用文件魔数解决 背景: 客户进行渗透测试,验证上传文件的程序没有对上传文件作任何过滤,导致可以上传任意文件到服务器,甚至是病毒文件和Webshell木马文件。 解决办法:对于上传的附件…...

LeetCode 热题 100 | 二叉树(二)
目录 1 543. 二叉树的直径 2 102. 二叉树的层序遍历 3 108. 将有序数组转换为二叉搜索树 菜鸟做题,语言是 C 1 543. 二叉树的直径 这道题和 124. 二叉树中的最大路径和 太像了 题眼:二叉树的 直径 是指树中任意两个节点之间 最长路径的长度 。…...
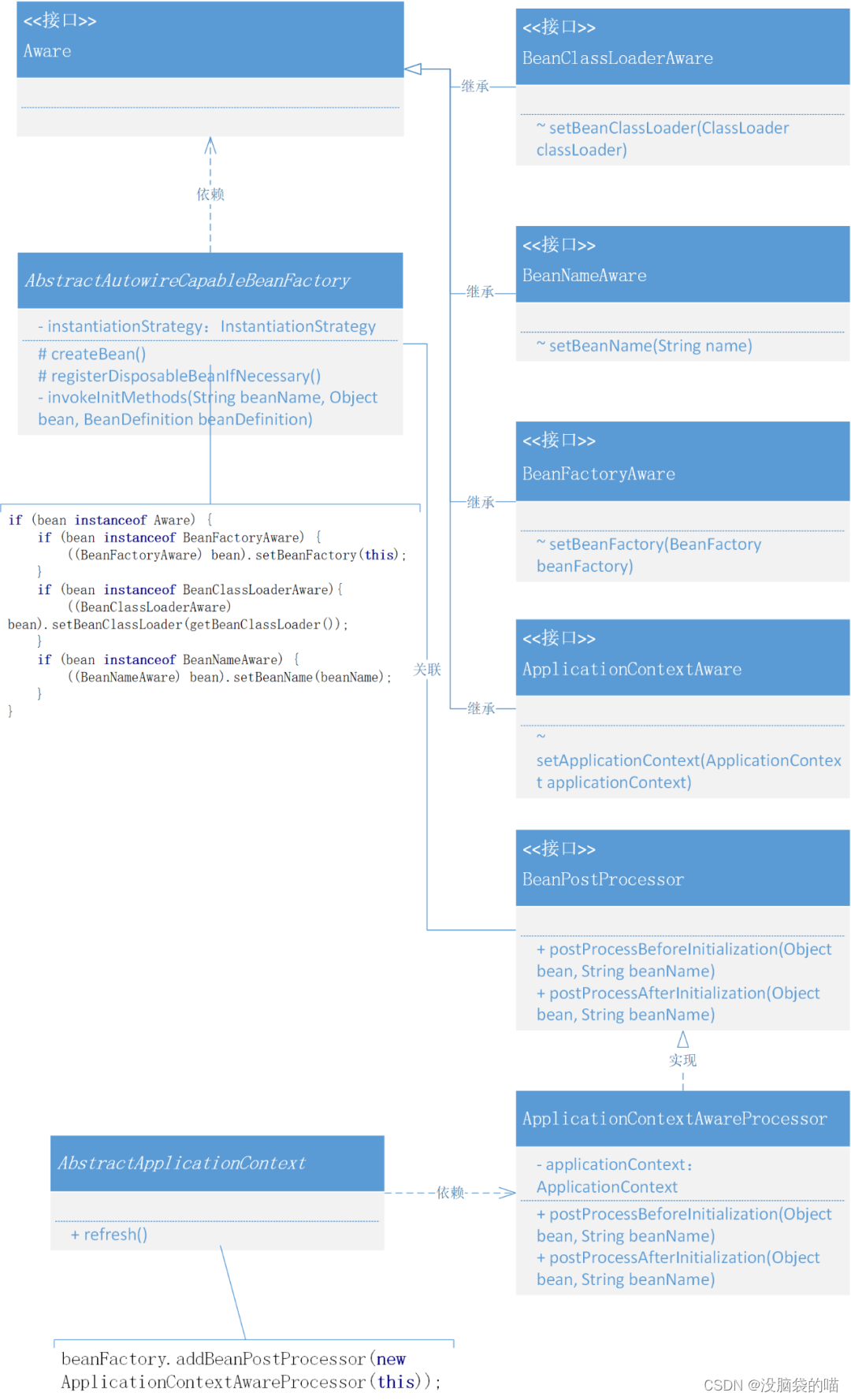
mini-spring|定义标记类型Aware接口,实现感知容器对象
**前言:**如果我们想获得 Spring 框架提供的 BeanFactory、ApplicationContext、BeanClassLoader等这些能力做一些扩展框架的使用时该怎么操作呢。所以我们本章节希望在 Spring 框架中提供一种能感知容器操作的接口,如果谁实现了这样的一个接口ÿ…...
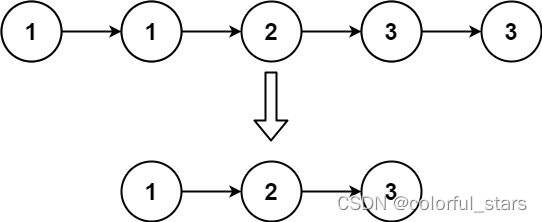
83. 删除排序链表中的重复元素
给定一个已排序的链表的头 head , 删除所有重复的元素,使每个元素只出现一次 。返回 已排序的链表 。 输入:head = [1,1,2] 输出:[1,2] 输入:head = [1,1,2,3,3] 输出:[1,2,3] 提示: 链表中节点数目在范围 [0, 300] 内-100 <= Node.val <= 100题目数据保证链表已…...

贪心算法
贪心算法 例题1、股票买卖题目信息思路题解 2、货仓选址题目信息思路题解 3、糖果传递题目信息思路题解 4、雷达设备题目信息思路题解 例题 1、股票买卖 题目信息 思路 相邻两天,后>前,则交易一次 题解 #include <bits/stdc.h> #define en…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...
