不平衡数据集的建模的技巧和策略
不平衡数据集是指一个类中的示例数量与另一类中的示例数量显著不同的情况。 例如在一个二元分类问题中,一个类只占总样本的一小部分,这被称为不平衡数据集。类不平衡会在构建机器学习模型时导致很多问题。
不平衡数据集的主要问题之一是模型可能会偏向多数类,从而导致预测少数类的性能不佳。这是因为模型经过训练以最小化错误率,并且当多数类被过度代表时,模型倾向于更频繁地预测多数类。这会导致更高的准确率得分,但少数类别得分较低。
另一个问题是,当模型暴露于新的、看不见的数据时,它可能无法很好地泛化。这是因为该模型是在倾斜的数据集上训练的,可能无法处理测试数据中的不平衡。
在本文中,我们将讨论处理不平衡数据集和提高机器学习模型性能的各种技巧和策略。将涵盖的一些技术包括重采样技术、代价敏感学习、使用适当的性能指标、集成方法和其他策略。通过这些技巧,可以为不平衡的数据集构建有效的模型。
处理不平衡数据集的技巧
重采样技术是处理不平衡数据集的最流行方法之一。这些技术涉及减少多数类中的示例数量或增加少数类中的示例数量。
欠采样可以从多数类中随机删除示例以减小其大小并平衡数据集。这种技术简单易行,但会导致信息丢失,因为它会丢弃一些多数类示例。
过采样与欠采样相反,过采样随机复制少数类中的示例以增加其大小。这种技术可能会导致过度拟合,因为模型是在少数类的重复示例上训练的。
SMOTE是一种更高级的技术,它创建少数类的合成示例,而不是复制现有示例。这种技术有助于在不引入重复项的情况下平衡数据集。
代价敏感学习(Cost-sensitive learning)是另一种可用于处理不平衡数据集的技术。在这种方法中,不同的错误分类成本被分配给不同的类别。这意味着与错误分类多数类示例相比,模型因错误分类少数类示例而受到更严重的惩罚。
在处理不平衡的数据集时,使用适当的性能指标也很重要。准确性并不总是最好的指标,因为在处理不平衡的数据集时它可能会产生误导。相反,使用 AUC-ROC等指标可以更好地指示模型性能。
集成方法,例如 bagging 和 boosting,也可以有效地对不平衡数据集进行建模。这些方法结合了多个模型的预测以提高整体性能。Bagging 涉及独立训练多个模型并对它们的预测进行平均,而 boosting 涉及按顺序训练多个模型,其中每个模型都试图纠正前一个模型的错误。
重采样技术、成本敏感学习、使用适当的性能指标和集成方法是一些技巧和策略,可以帮助处理不平衡的数据集并提高机器学习模型的性能。
在不平衡数据集上提高模型性能的策略
收集更多数据是在不平衡数据集上提高模型性能的最直接策略之一。通过增加少数类中的示例数量,模型将有更多信息可供学习,并且不太可能偏向多数类。当少数类中的示例数量非常少时,此策略特别有用。
生成合成样本是另一种可用于提高模型性能的策略。合成样本是人工创建的样本,与少数类中的真实样本相似。这些样本可以使用 SMOTE等技术生成,该技术通过在现有示例之间进行插值来创建合成示例。生成合成样本有助于平衡数据集并为模型提供更多示例以供学习。
使用领域知识来关注重要样本也是一种可行的策略,通过识别数据集中信息量最大的示例来提高模型性能。例如,如果我们正在处理医学数据集,可能知道某些症状或实验室结果更能表明某种疾病。通过关注这些例子可以提高模型准确预测少数类的能力。
最后可以使用异常检测等高级技术来识别和关注少数类示例。这些技术可用于识别与多数类不同且可能是少数类示例的示例。这可以通过识别数据集中信息量最大的示例来帮助提高模型性能。
在收集更多数据、生成合成样本、使用领域知识专注于重要样本以及使用异常检测等先进技术是一些可用于提高模型在不平衡数据集上的性能的策略。这些策略可以帮助平衡数据集,为模型提供更多示例以供学习,并识别数据集中信息量最大的示例。
不平衡数据集的练习
这里我们使用信用卡欺诈分类的数据集演示处理不平衡数据的方法
import pandas as pd
import numpy as np
from sklearn.preprocessing import RobustScaler
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.metrics import confusion_matrix, classification_report,f1_score,recall_score,roc_auc_score, roc_curve
import matplotlib.pyplot as plt
import seaborn as sns
from matplotlib import rc,rcParams
import itertools
import warnings
warnings.filterwarnings("ignore", category=DeprecationWarning)
warnings.filterwarnings("ignore", category=FutureWarning)
warnings.filterwarnings("ignore", category=UserWarning)
读取数据
df = pd.read_csv("creditcard.csv")
df.head()
print("Number of observations : " ,len(df))
print("Number of variables : ", len(df.columns))
#Number of observations : 284807
#Number of variables : 31
查看数据集信息
df.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 284807 entries, 0 to 284806
Data columns (total 31 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Time 284807 non-null float64
1 V1 284807 non-null float64
2 V2 284807 non-null float64
3 V3 284807 non-null float64
4 V4 284807 non-null float64
5 V5 284807 non-null float64
6 V6 284807 non-null float64
7 V7 284807 non-null float64
8 V8 284807 non-null float64
9 V9 284807 non-null float64
10 V10 284807 non-null float64
11 V11 284807 non-null float64
12 V12 284807 non-null float64
13 V13 284807 non-null float64
14 V14 284807 non-null float64
15 V15 284807 non-null float64
16 V16 284807 non-null float64
17 V17 284807 non-null float64
18 V18 284807 non-null float64
19 V19 284807 non-null float64
20 V20 284807 non-null float64
21 V21 284807 non-null float64
22 V22 284807 non-null float64
23 V23 284807 non-null float64
24 V24 284807 non-null float64
25 V25 284807 non-null float64
26 V26 284807 non-null float64
27 V27 284807 non-null float64
28 V28 284807 non-null float64
29 Amount 284807 non-null float64
30 Class 284807 non-null int64
dtypes: float64(30), int64(1)
memory usage: 67.4 MB
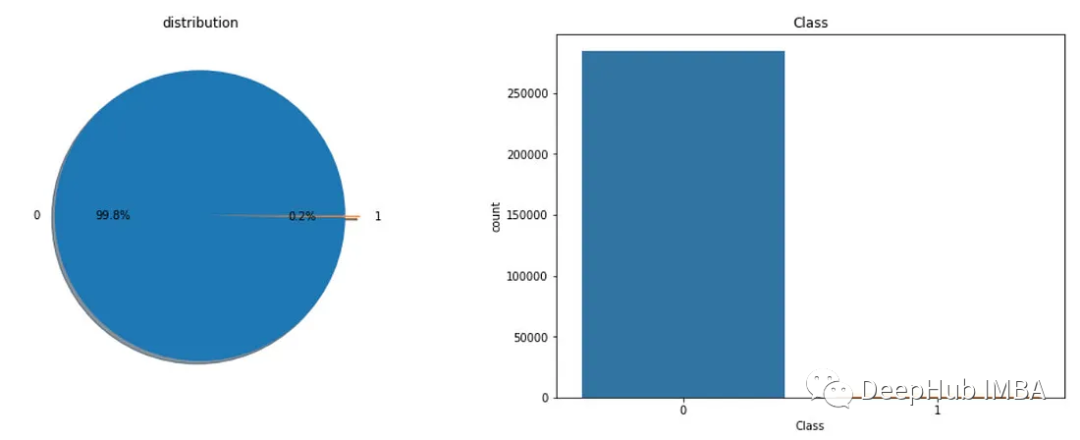
查看分类类别:
f,ax=plt.subplots(1,2,figsize=(18,8))
df['Class'].value_counts().plot.pie(explode=[0,0.1],autopct='%1.1f%%',ax=ax[0],shadow=True)
ax[0].set_title('dağılım')
ax[0].set_ylabel('')
sns.countplot('Class',data=df,ax=ax[1])
ax[1].set_title('Class')
plt.show()
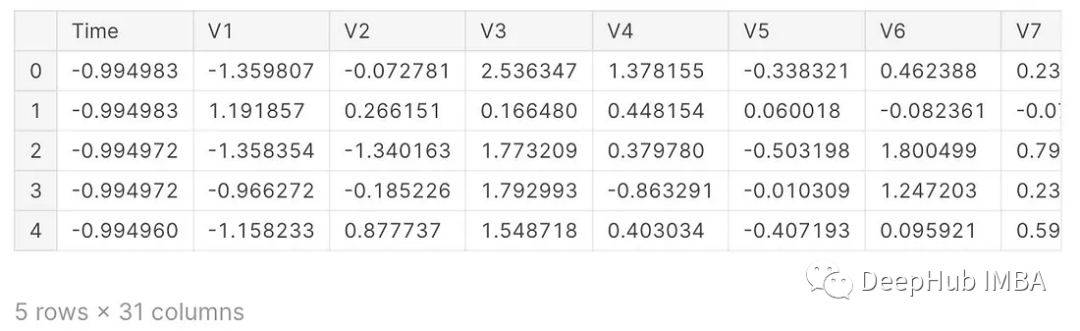
rob_scaler = RobustScaler()
df['Amount'] = rob_scaler.fit_transform(df['Amount'].values.reshape(-1,1))
df['Time'] = rob_scaler.fit_transform(df['Time'].values.reshape(-1,1))
df.head()
创建基类模型
X = df.drop("Class", axis=1)
y = df["Class"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.20, random_state=123456)
model = LogisticRegression(random_state=123456)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy: %.3f"%(accuracy))
我们创建的模型的准确率评分为0.999。我们可以说我们的模型很完美吗?
混淆矩阵是一个用来描述分类模型的真实值在测试数据上的性能的表。它包含4种不同的估计值和实际值的组合。
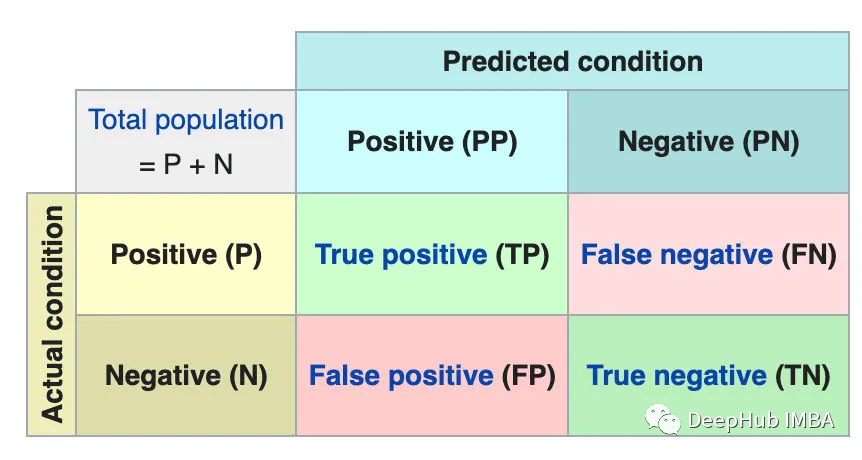
def plot_confusion_matrix(cm, classes,
title='Confusion matrix',
cmap=plt.cm.Blues):
plt.rcParams.update({'font.size': 19})
plt.imshow(cm, interpolation='nearest', cmap=cmap)
plt.title(title,fontdict={'size':'16'})
plt.colorbar()
tick_marks = np.arange(len(classes))
plt.xticks(tick_marks, classes, rotation=45,fontsize=12,color="blue")
plt.yticks(tick_marks, classes,fontsize=12,color="blue")
rc('font', weight='bold')
fmt = '.1f'
thresh = cm.max()
for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
plt.text(j, i, format(cm[i, j], fmt),
horizontalalignment="center",
color="red")
plt.ylabel('True label',fontdict={'size':'16'})
plt.xlabel('Predicted label',fontdict={'size':'16'})
plt.tight_layout()
plot_confusion_matrix(confusion_matrix(y_test, y_pred=y_pred), classes=['Non Fraud','Fraud'],
title='Confusion matrix')
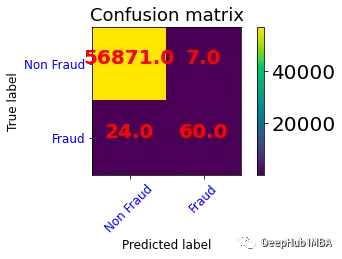
•非欺诈类共进行了56875次预测,其中56870次(TP)正确,5次(FP)错误。
•欺诈类共进行了87次预测,其中31次(FN)错误,56次(TN)正确。
该模型可以预测欺诈状态,准确率为0.99。但当检查混淆矩阵时,欺诈类的错误预测率相当高。也就是说该模型正确地预测了非欺诈类的概率为0.99。但是非欺诈类的观测值的数量高于欺诈类的观测值的数量,这拉搞了我们对准确率的计算,并且我们更加关注的是欺诈类的准确率,所以我们需要一个指标来衡量它的性能。
选择正确的指标
在处理不平衡数据集时,选择正确的指标来评估模型的性能非常重要。传统指标,如准确性、精确度和召回率,可能不适用于不平衡的数据集,因为它们没有考虑数据中类别的分布。
经常用于不平衡数据集的一个指标是 F1 分数。F1 分数是精确率和召回率的调和平均值,它提供了两个指标之间的平衡。计算如下:
F1 = 2 * (precision * recall) / (precision + recall)
另一个经常用于不平衡数据集的指标是 AUC-ROC。AUC-ROC 衡量模型区分正类和负类的能力。它是通过绘制不同分类阈值下的TPR与FPR来计算的。AUC-ROC 值的范围从 0.5(随机猜测)到 1.0(完美分类)。
print(classification_report(y_test, y_pred))
precision recall f1-score support
0 1.00 1.00 1.00 56875
1 0.92 0.64 0.76 87
accuracy 1.00 56962
macro avg 0.96 0.82 0.88 56962
weighted avg 1.00 1.00 1.00 56962
返回对0(非欺诈)类的预测有多少是正确的。查看混淆矩阵,56870 + 31 = 56901个非欺诈类预测,其中56870个预测正确。0类的精度值接近1 (56870 / 56901)
返回对1 (欺诈)类的预测有多少是正确的。查看混淆矩阵,5 + 56 = 61个欺诈类别预测,其中56个被正确估计。0类的精度为0.92 (56 / 61),可以看到差别还是很大的
过采样
通过复制少数类样本来稳定数据集。
随机过采样:通过添加从少数群体中随机选择的样本来平衡数据集。如果数据集很小,可以使用这种技术。可能会导致过拟合。randomoverampler方法接受sampling_strategy参数,当sampling_strategy = ' minority '被调用时,它会增加minority类的数量,使其与majority类的数量相等。
我们可以在这个参数中输入一个浮点值。例如,假设我们的少数群体人数为1000人,多数群体人数为100人。如果我们说sampling_strategy = 0.5,少数类将被添加到500。
y_train.value_counts()
0 227440
1 405
Name: Class, dtype: int64
from imblearn.over_sampling import RandomOverSampler
oversample = RandomOverSampler(sampling_strategy='minority')
X_randomover, y_randomover = oversample.fit_resample(X_train, y_train)
采样后训练
model.fit(X_randomover, y_randomover)
y_pred = model.predict(X_test)
plot_confusion_matrix(confusion_matrix(y_test, y_pred=y_pred), classes=['Non Fraud','Fraud'],
title='Confusion matrix')
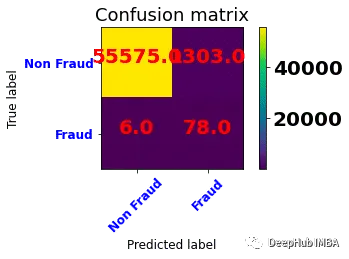
应用随机过采样后,训练模型的精度值为0.97,出现了下降。但是从混淆矩阵来看,模型的欺诈类的正确估计率有所提高。
SMOTE 过采样:从少数群体中随机选取一个样本。然后,为这个样本找到k个最近的邻居。从k个最近的邻居中随机选取一个,将其与从少数类中随机选取的样本组合在特征空间中形成线段,形成合成样本。
from imblearn.over_sampling import SMOTE
oversample = SMOTE()
X_smote, y_smote = oversample.fit_resample(X_train, y_train)
使用SMOTE后的数据训练
model.fit(X_smote, y_smote)
y_pred = model.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
plot_confusion_matrix(confusion_matrix(y_test, y_pred=y_pred), classes=['Non Fraud','Fraud'],
title='Confusion matrix')
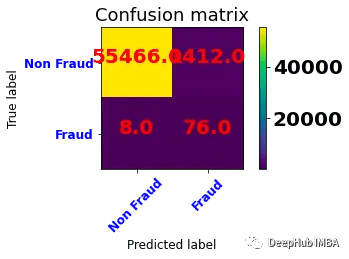
可以看到与基线模型相比,欺诈的准确率有所提高,但是比随机过采样有所下降,这可能是数据集的原因,因为SMOTE采样会生成心的数据,所以并不适合所有的数据集。
总结
在这篇文章中,我们讨论了处理不平衡数据集和提高机器学习模型性能的各种技巧和策略。不平衡的数据集可能是机器学习中的一个常见问题,并可能导致在预测少数类时表现不佳。
本文介绍了一些可用于平衡数据集的重采样技术,如欠采样、过采样和SMOTE。还讨论了成本敏感学习和使用适当的性能指标,如AUC-ROC,这可以提供更好的模型性能指示。
处理不平衡的数据集是具有挑战性的,但通过遵循本文讨论的技巧和策略,可以建立有效的模型准确预测少数群体。重要的是要记住最佳方法将取决于特定的数据集和问题,为了获得最佳结果,可能需要结合各种技术。因此,试验不同的技术并使用适当的指标评估它们的性能是很重要的。
作者:Emine Bozkuş
相关文章:

不平衡数据集的建模的技巧和策略
不平衡数据集是指一个类中的示例数量与另一类中的示例数量显著不同的情况。 例如在一个二元分类问题中,一个类只占总样本的一小部分,这被称为不平衡数据集。类不平衡会在构建机器学习模型时导致很多问题。不平衡数据集的主要问题之一是模型可能会偏向多数…...

3. 算法效率
同一个问题的不同算法在性能上的比较,现在的方法主要是算法时间复杂度。算法效率是算法操作(operate)或处理(treat)数据的重复次数最小。 例题选自《编程珠玑》第8章,算法设计技术。 这个问题是一维模式识别(人工智能)中的一个问题。 输入有n个元素的向量,输出连续子向…...

仪表放大器放大倍数分析-运算放大器
仪表放大器是一种非常特殊的精密差分电压放大器,它的主要特点是采用差分输入、具有很高的输入阻抗和共模抑制比,能够有效放大在共模电压干扰下的信号。本文简单分析一下三运放仪表放大器的放大倍数。 一、放大倍数理论分析 三运放仪表放大器的电路结构…...
laravel8多模块、多应用和多应用路由
1、安装多应用模块 composer require nwidart/laravel-modules2、执行命令,config文件夹下生成一个modules.php配置文件 php artisan vendor:publish --provider"Nwidart\Modules\LaravelModulesServiceProvider"3、修改config文件夹下的modules.php&am…...

【Java学习笔记】6.Java 变量类型
Java 变量类型 在Java语言中,所有的变量在使用前必须声明。声明变量的基本格式如下: type identifier [ value][, identifier [ value] ...] ;格式说明:type为Java数据类型。identifier是变量名。可以使用逗号隔开来声明多个同类型变量。 …...

Promise对象状态属性 工作流程 Promise对象的几个属性
Promise 对象状态属性介绍 实例对象中的一个属性 PromiseState pending 1、pending 变为 resolved / fullfilled 成功 2、pending 变为 rejected 失败 说明:只有这2种,且一个promise对象只能改变一次 无论变为成功还是失败,都会有一个结果…...

webgpu思考obj携带属性
今天在搞dbbh.js的时候,想到一个问题,啥问题呢,先看看情况 画2个材质不相同的box的时候 首先开始createCommandEncoder,然后beginRenderPass,分歧就在这里了 第一个box,他有自己的pipeline,第二个也有,那么…...
设计模式(只谈理解,没有代码)
1.什么是设计模式设计模式,是一套被反复使用、多数人知晓的、经过分类编目的、代码设计经验的总结。使用设计模式是为了可重用代码、让代码更容易被他人理解、保证代码可靠性、程序的重用性。2.为什么要学习设计模式看懂源代码:如果你不懂设计模式去看Jd…...

06、Eclipse 中使用 SVN
Eclipse 中使用 SVN1 在 Eclipse 中安装 SVN 客户端插件1.1 在线安装1.2 离线安装2 SVN 在 Eclipse 分享3 检出提交更新3.1 检出3.2 提交3.3 更新4 Eclipse 中 SVN 图标及其含义4.1 ?图标4.2 图标4.3 金色圆柱图标4.4 * 图标5 恢复历史版本5.1 恢复步骤5.2 权限控制…...

Zookeeper3.5.7版本——客户端命令行操作(命令行语法)
目录一、命令行语法二、help命令行语法示例一、命令行语法 命令行语法列表 命令基本语法功能描述help显示所有操作命令ls path使用 ls 命令来查看当前 znode 的子节点 [可监听]-w 监听子节点变化-s 附加次级信息create普通创建-s 含有序列-e 临时(重启或者超时消失…...

2023.03.05 学习周报
文章目录摘要文献阅读1.题目2.摘要3.介绍4.SAMPLING THE OUTPUT5.LOSS FUNCTION DESIGN5.1 ranking loss: Top1 & BPR5.2 VANISHING GRADIENTS5.3 ranking-max loss fuction5.4 BPR-max with score regularization6.实验7.结论深度学习1.相关性1.1 什么是相关性1.2 协方差1…...
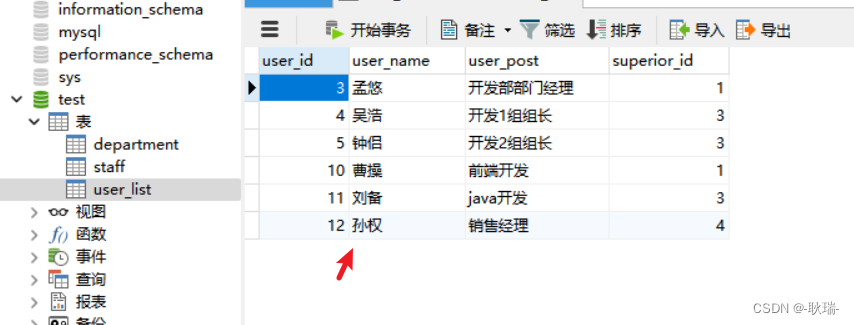
java Spring JdbcTemplate配合mysql实现数据批量修改
其实这个操作和批量添加挺像的 调的同一个方法 首先 我们看数据库结构 这是我本地的 mysql 里面有一个test数据库 里面有一张user_list表 然后创建一个java项目 然后 引入对应的JAR包 在src下创建 dao 目录 在下面创建一个接口 叫 BookDao 参考代码如下 package dao;impo…...
《算法分析与设计》笔记总结
《算法分析与设计》笔记总结第一章 算法引论1.1 算法与程序1.2 表达算法的抽象机制1.3 描述算法1.4 算法复杂性分析第二章 递归与分治策略2.1 递归的概念2.2 分治法的基本思想2.3 二分搜索技术2.4 大整数乘法2.5 Strassen矩阵乘法2.7 合并排序2.8 快速排序2.9 线性时间选择2.10…...

序列化与反序列化概念
序列化是指将对象的状态信息转换为可以存储或传输的形式的过程。 在Java中创建的对象,只要没有被回收就可以被复用,但是,创建的这些对象都是存在于JVM的堆内存中,JVM处于运行状态时候,这些对象可以复用, 但…...
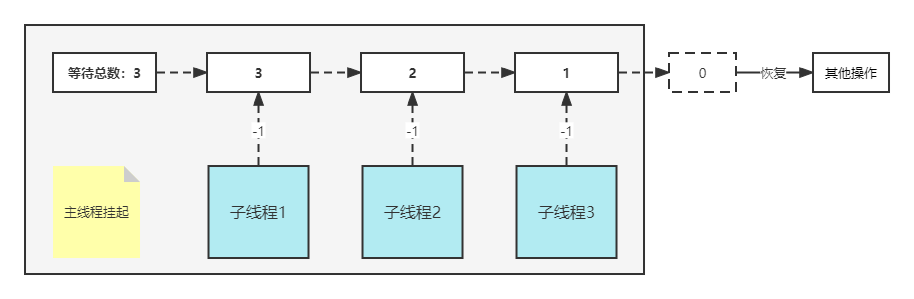
【Java并发编程】CountDownLatch
CountDownLatch是JUC提供的解决方案 CountDownLatch 可以保证一组子线程全部执行完牛后再进行主线程的执行操作。例如,主线程启动前,可能需要启动并执行若干子线程,这时就可以通过 CountDownLatch 来进行控制。 CountDownLatch是通过一个线程…...

【iOS】Blocks
BlockBlocks概要什么是Blocks?Block语法Block类型变量截获自动变量值__block说明符Blocks的实现Block的实质Blocks概要 什么是Blocks? Blocks可简单概括为: 带有自动变量(局部变量)的匿名函数 在使用Blocks时&#x…...
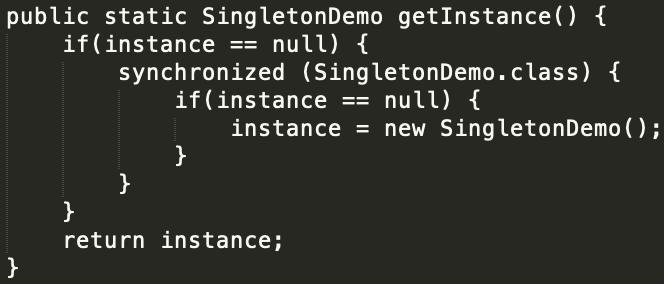
Java Volatile的三大特性
本文通过学习:周阳老师-尚硅谷Java大厂面试题第二季 总结的volatile相关的笔记volatile是Java虚拟机提供的轻量级的同步机制,三大特性为:保证可见性、不保证原子性、禁止指令重排一、保证可见性import java.util.concurrent.TimeUnit;class M…...
Android Compose——一个简单的Bilibili APP
Bilibili移动端APP简介依赖效果登录效果WebView自定义TobRow的Indicator大小首页推荐LazyGridView使用Paging3热门排行榜搜索模糊搜索富文本搜索结果视频详情合集信息Coroutines进行网络请求管理,避免回调地狱添加suspendwithContextGit项目链接末简介 此Demo采用A…...
二叉树的最近公共祖先【Java实现】
题目描述 现有一棵n个结点的二叉树(结点编号为从0到n-1,根结点为0号结点),求两个指定编号结点的最近公共祖先。 注:二叉树上两个结点A、B的最近公共祖先是指:二叉树上存在的一个结点P,使得P既是…...
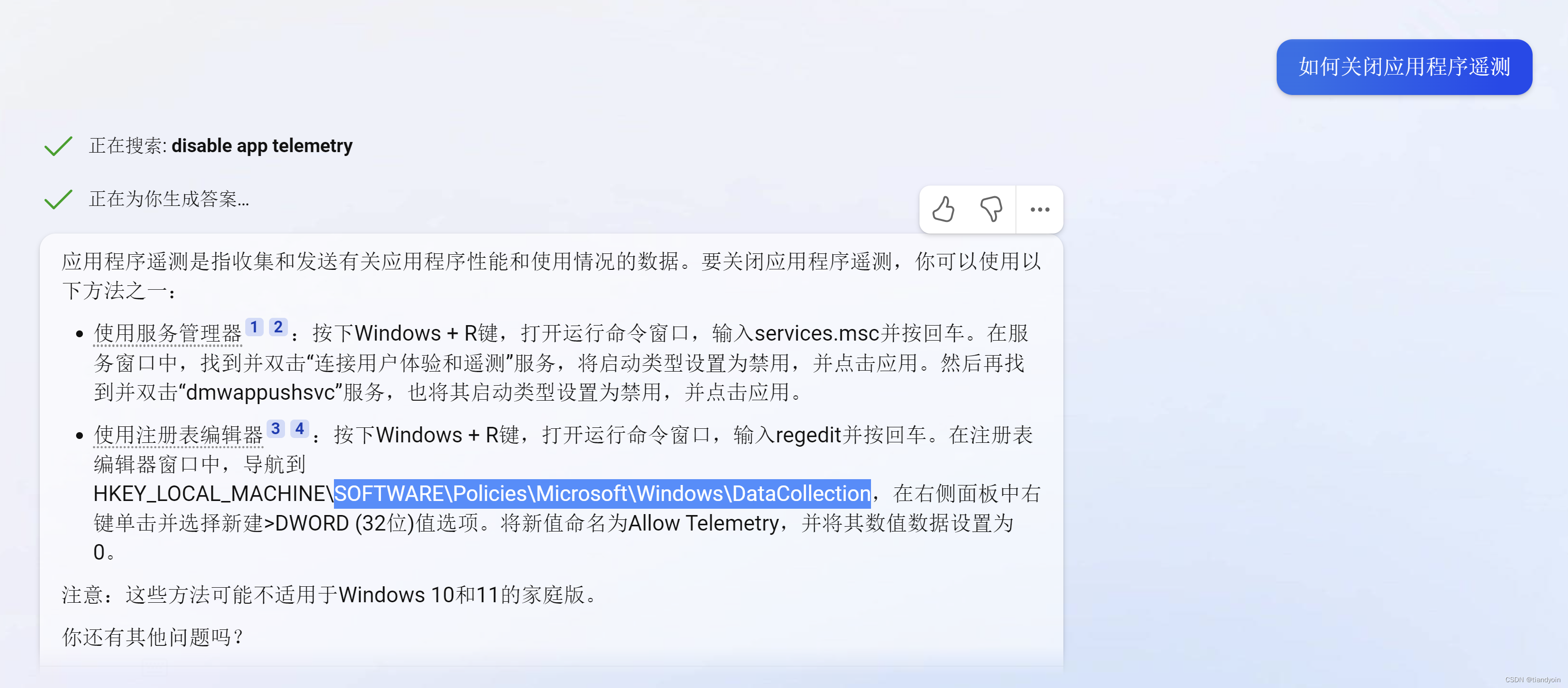
关闭应用程序遥测,禁止Windows收集用户信息
目录 1. 先创建还原点,防止意外 2. 界面设置 3. 服务 (1) GPEdit.msc - 本地计算机策略 - 计算机配置 - 管理模板 - Windows 组件 - 应用程序兼容性 - 关闭应用程序遥测 - 已启用 (2) GPEdit.msc - 本地计算机策略 - 计算机配置 - 管理模板 - Windows 组件 - 数…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...
