神经网络系列---权重初始化方法
文章目录
- 权重初始化方法
- Xavier初始化(Xavier initialization)
- Kaiming初始化,也称为He初始化
- LeCun 初始化
- 正态分布与均匀分布
- Orthogonal Initialization
- Sparse Initialization
- n_in和n_out
- 代码实现
权重初始化方法
Xavier初始化(Xavier initialization)
是一种用于初始化神经网络权重的方法,也称为Glorot初始化。更有效地传播信号并减少梯度消失或梯度爆炸的问题。适用于激活函数为tanh或sigmoid的情况。
Xavier初始化的计算方法如下:
- Glorot(或 Xavier)初始化:
- 适用于激活函数如sigmoid和tanh。
- 初始化公式: σ = 2 n in + n out \sigma = \sqrt{\frac{2}{n_{\text{in}} + n_{\text{out}}}} σ=nin+nout2
其中, n in n_{\text{in}} nin 是输入单元数, n out n_{\text{out}} nout 是输出单元数。
对于单个神经元的权重w,从均匀分布或正态分布中随机采样,具体取决于所选择的激活函数:
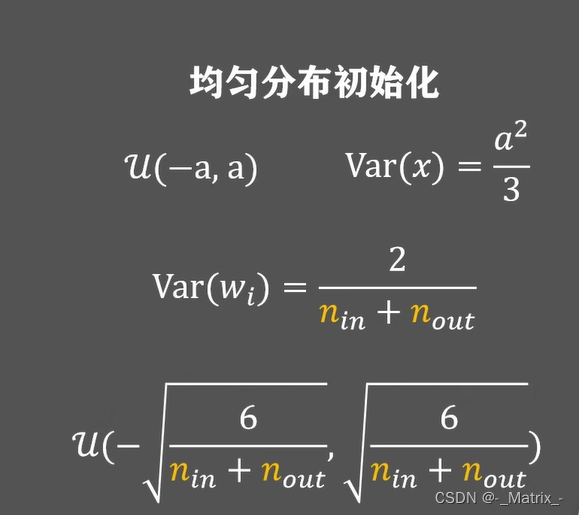
- 如果使用
tanh激活函数,从均匀分布采样:- 采样范围:
[-sqrt(6 / (n_in + n_out)), sqrt(6 / (n_in + n_out))] - 其中
n_in是上一层的输入节点数量,n_out是当前层的输出节点数量。
- 采样范围:
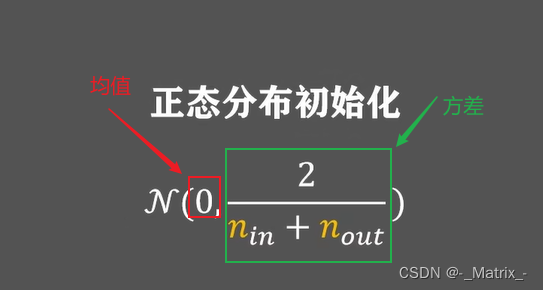
- 如果使用
sigmoid激活函数,从正态分布采样:- 均值:0
- 方差:
sqrt(2 / (n_in + n_out)) - 其中n_in是上一层的输入节点数量,n_out是当前层的输出节点数量。
Kaiming初始化,也称为He初始化
- He 初始化:
- 适用于ReLU及其变种(如LeakyReLU)激活函数。
- 初始化公式: σ = 2 n in \sigma = \sqrt{\frac{2}{n_{\text{in}}}} σ=nin2
这种初始化方法主要用于修正线性单元(Rectified Linear Units,ReLU)激活函数的神经网络。
与Xavier初始化适用于tanh和sigmoid等S型激活函数不同,Kaiming初始化专门针对ReLU激活函数的特性进行优化。ReLU是一个常用的非线性激活函数,它在输入大于零时保持不变,在输入小于等于零时输出为零。
Kaiming初始化的计算方法如下:
对于单个神经元的权重w,从均匀分布或正态分布中随机采样,具体取决于所选择的激活函数:
-
如果使用
ReLU激活函数,从正态分布采样:- 均值:0
- 方差:
sqrt(2 / n_in) - 其中n_in是上一层的输入节点数量。
-
对于带有ReLU激活的卷积层,可以使用相同的初始化方法,只是需要考虑卷积层的输入通道数量(即n_in)。
LeCun 初始化
- 适用于Sigmoid激活函数。
- 初始化公式: σ = 1 n in \sigma = \sqrt{\frac{1}{n_{\text{in}}}} σ=nin1
正态分布与均匀分布
- 使用较小的标准差(如0.01)从正态分布中采样权重。
- 使用较小的范围(如-0.01到0.01)从均匀分布中采样权重。
Orthogonal Initialization
- 使用正交矩阵初始化权重。这种初始化方法对于某些任务和模型架构可能很有益。
Sparse Initialization
- 将大部分权重初始化为0,只初始化一小部分非零的权重。
n_in和n_out
n_in和n_out分别表示神经网络层的输入节点数量和输出节点数量。这些节点也称为神经元,它们是网络的基本组成部分。
-
n_in:代表上一层(前一层)的节点数量,也就是当前层的输入数量。在神经网络中,每个神经元都会接收来自上一层所有节点的输入,这些输入被加权和后传递给当前神经元的激活函数。因此,n_in指的是上一层与当前层之间的连接数量。
-
n_out:代表当前层的节点数量,也就是当前层的输出数量。每个神经元会将经过激活函数处理后的结果传递给下一层所有节点,形成下一层的输入。因此,n_out指的是当前层与下一层之间的连接数量。
代码实现
#include <iostream>
#include <Eigen/Dense>
#include <random>
#include <cmath>Eigen::MatrixXd glorotInitialize(int rows, int cols);
Eigen::MatrixXd heInitialize(int rows, int cols);
Eigen::MatrixXd lecunInitialize(int rows, int cols);
Eigen::MatrixXd normalDistributionInitialize(int rows, int cols, double std_dev=0.01);
Eigen::MatrixXd uniformDistributionInitialize(int rows, int cols, double limit=0.01);
Eigen::MatrixXd orthogonalInitialize(int rows, int cols);
// Sparse Initialization需要额外参数来确定稀疏度,这里我们使用一个简化版本,指定一个非零的权重数。
Eigen::MatrixXd sparseInitialize(int rows, int cols, int nonZeroCount);//1. **Glorot (Xavier) Initialization**:Eigen::MatrixXd glorotInitialize(int rows, int cols) {std::random_device rd;std::mt19937 gen(rd());double limit = sqrt(6.0 / (rows + cols));std::uniform_real_distribution<> dis(-limit, limit);Eigen::MatrixXd matrix(rows, cols);for(int i = 0; i < rows; i++) {for(int j = 0; j < cols; j++) {matrix(i, j) = dis(gen);}}return matrix;
}//**He Initialization**:Eigen::MatrixXd heInitialize(int rows, int cols) {std::random_device rd;std::mt19937 gen(rd());double std_dev = sqrt(2.0 / rows);std::normal_distribution<> dis(0, std_dev);Eigen::MatrixXd matrix(rows, cols);for(int i = 0; i < rows; i++) {for(int j = 0; j < cols; j++) {matrix(i, j) = dis(gen);}}return matrix;
}//3. **LeCun Initialization**:Eigen::MatrixXd lecunInitialize(int rows, int cols) {std::random_device rd;std::mt19937 gen(rd());double std_dev = sqrt(1.0 / rows);std::normal_distribution<> dis(0, std_dev);Eigen::MatrixXd matrix(rows, cols);for(int i = 0; i < rows; i++) {for(int j = 0; j < cols; j++) {matrix(i, j) = dis(gen);}}return matrix;
}//4. **Normal Distribution Initialization**:Eigen::MatrixXd normalDistributionInitialize(int rows, int cols, double std_dev) {std::random_device rd;std::mt19937 gen(rd());std::normal_distribution<> dis(0, std_dev);Eigen::MatrixXd matrix(rows, cols);for(int i = 0; i < rows; i++) {for(int j = 0; j < cols; j++) {matrix(i, j) = dis(gen);}}return matrix;
}//5. **Uniform Distribution Initialization**:Eigen::MatrixXd uniformDistributionInitialize(int rows, int cols, double limit) {std::random_device rd;std::mt19937 gen(rd());std::uniform_real_distribution<> dis(-limit, limit);Eigen::MatrixXd matrix(rows, cols);for(int i = 0; i < rows; i++) {for(int j = 0; j < cols; j++) {matrix(i, j) = dis(gen);}}return matrix;
}//6. **Orthogonal Initialization**:
Eigen::MatrixXd orthogonalInitialize(int rows, int cols) {// 创建一个随机矩阵std::random_device rd;std::mt19937 gen(rd());std::normal_distribution<> dis(0, 1);Eigen::MatrixXd randomMatrix(rows, cols);for(int i = 0; i < rows; i++) {for(int j = 0; j < cols; j++) {randomMatrix(i, j) = dis(gen);}}// 使用QR分解获得正交矩阵Eigen::HouseholderQR<Eigen::MatrixXd> qr(randomMatrix);Eigen::MatrixXd orthogonalMatrix = qr.householderQ();// 如果您需要一个具有特定维度的正交矩阵(例如rows != cols),您可以选择一个子矩阵return orthogonalMatrix.block(0, 0, rows, cols);
}//7. **Sparse Initialization**:Eigen::MatrixXd sparseInitialize(int rows, int cols, int nonZeroCount) {Eigen::MatrixXd matrix = Eigen::MatrixXd::Zero(rows, cols);std::random_device rd;std::mt19937 gen(rd());std::uniform_real_distribution<> dis(-1, 1);for(int i = 0; i < nonZeroCount; i++) {int r = rand() % rows;int c = rand() % cols;matrix(r, c) = dis(gen);}return matrix;
}
int main() {int rows = 5;int cols = 5;// Glorot InitializationEigen::MatrixXd weights_glorot = glorotInitialize(rows, cols);std::cout << "Glorot Initialized Weights:" << std::endl << weights_glorot << std::endl << std::endl;// He InitializationEigen::MatrixXd weights_he = heInitialize(rows, cols);std::cout << "He Initialized Weights:" << std::endl << weights_he << std::endl << std::endl;// LeCun InitializationEigen::MatrixXd weights_lecun = lecunInitialize(rows, cols);std::cout << "LeCun Initialized Weights:" << std::endl << weights_lecun << std::endl << std::endl;// Normal Distribution InitializationEigen::MatrixXd weights_normal = normalDistributionInitialize(rows, cols);std::cout << "Normal Distribution Initialized Weights:" << std::endl << weights_normal << std::endl << std::endl;// Uniform Distribution InitializationEigen::MatrixXd weights_uniform = uniformDistributionInitialize(rows, cols);std::cout << "Uniform Distribution Initialized Weights:" << std::endl << weights_uniform << std::endl << std::endl;// Sparse Initializationint nonZeroCount = 10; // As an example, set 10 weights to non-zero valuesEigen::MatrixXd weights_sparse = sparseInitialize(rows, cols, nonZeroCount);std::cout << "Sparse Initialized Weights with " << nonZeroCount << " non-zero values:" << std::endl << weights_sparse << std::endl;return 0;
}相关文章:

神经网络系列---权重初始化方法
文章目录 权重初始化方法Xavier初始化(Xavier initialization)Kaiming初始化,也称为He初始化LeCun 初始化正态分布与均匀分布Orthogonal InitializationSparse Initializationn_in和n_out代码实现 权重初始化方法 Xavier初始化(X…...

【重要公告】BSV区块链协会宣布将启动多项动态安全增强措施
发表时间:2024年2月16日 2024年2月16日,瑞士楚格 - BSV区块链协议的管理机构BSV区块链协会(以下简称“BSV协会”)宣布对其运营模式实施全新的安全架构,其中包括引入网络访问规则和数字资产找回协议,以及…...
)
软件设计模式之访问者模式(Visitor Pattern)
访问者模式是一种行为型设计模式,它允许你定义一系列操作,这些操作可以应用于对象结构中的元素,而不改变这些元素的类。通过这种方式,可以在不改变各个元素的类的情况下,增加新的操作。 1. 何时使用访问者模式&#x…...
【MySQL】主从同步原理、分库分表
主从同步原理 1. 主从同步原理 MySQL 经常先把命令拷入硬盘的日志,再执行日志的命令,这样的好处: 日志的位置固定,拷入硬盘的开销不大;将命令先准备好,而不是边读边执行,性能更好,…...

uniapp如何实现关闭前面指定数目页面
需求 : 路由从 页面A -> 页面B-> 页面C-> 页面D 我希望在 页面C跳到页面CD 后 在页面D 中 点击返回(物理键或是代码返回),直接返回到A,而不是页面C 所以我需要把BC页面给销毁掉 以下是我的实现思路,在h…...
使用 Helm 安装 极狐GitLab
本篇作者 徐晓伟 使用 Helm 简便快捷的部署与管理 极狐GitLab 前提条件 k8s 完成 helm 的配置 k8s 完成 ingress 的配置 内存至少 10G 演示环境是 龙蜥 Anolis 8.4(即:CentOS 8.4)最小化安装k8s 版本 1.28.2calico 版本 3.26.1nginx ingre…...

K8S部署postgresql
(作者:陈玓玏) 一、前置条件 已部署k8s,服务端版本为1.21.14 二、部署postgresql 拉取镜像,docker pull postgres,不指定版本,自动从docker hub拉取最新版本;配置configmap&…...

Go 如何控制并发的goroutine数量?
为什么要控制goroutine并发的数量? 在开发过程中,如果不对goroutine加以控制而进行滥用的话,可能会导致服务整体崩溃。比如耗尽系统资源导致程序崩溃,或者CPU使用率过高导致系统忙不过来。 用什么方法控制goroutine并发的数量&a…...

【黑马程序员】1、TypeScript介绍_黑马程序员前端TypeScript教程,TypeScript零基础入门到实战全套教程
课程地址:【黑马程序员前端TypeScript教程,TypeScript零基础入门到实战全套教程】 https://www.bilibili.com/video/BV14Z4y1u7pi/?share_sourcecopy_web&vd_sourceb1cb921b73fe3808550eaf2224d1c155 目录 1、TypeScript介绍 1.1 TypeScript是什…...
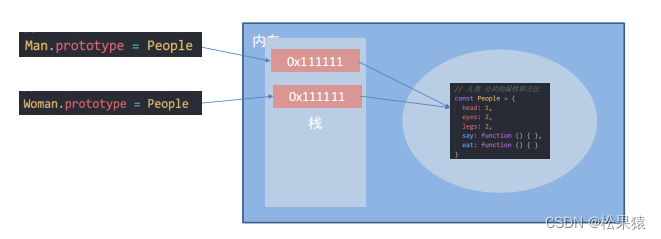
JS进阶——深入对象
构造函数 封装是面向对象思想中比较重要的一部分,js面向对象可以通过构造函数实现的封装。 前面我们学过的构造函数方法很好用,但是 存在浪费内存的问题 原型 目标:能够利用原型对象实现方法共享 构造函数通过原型分配的函数是所有对象所…...

Gitlab部署管理
一、安装 1.docker安装gitlab sudo docker run -d \-p 6080:80 -p 6022:22 \--name gitlab \--restart always \-v /srv/gitlab/config:/etc/gitlab \-v /srv/gitlab/logs:/var/log/gitlab \-v /srv/gitlab/data:/var/opt/gitlab \gitlab/gitlab-ce:latest2.存储说明 存储应…...
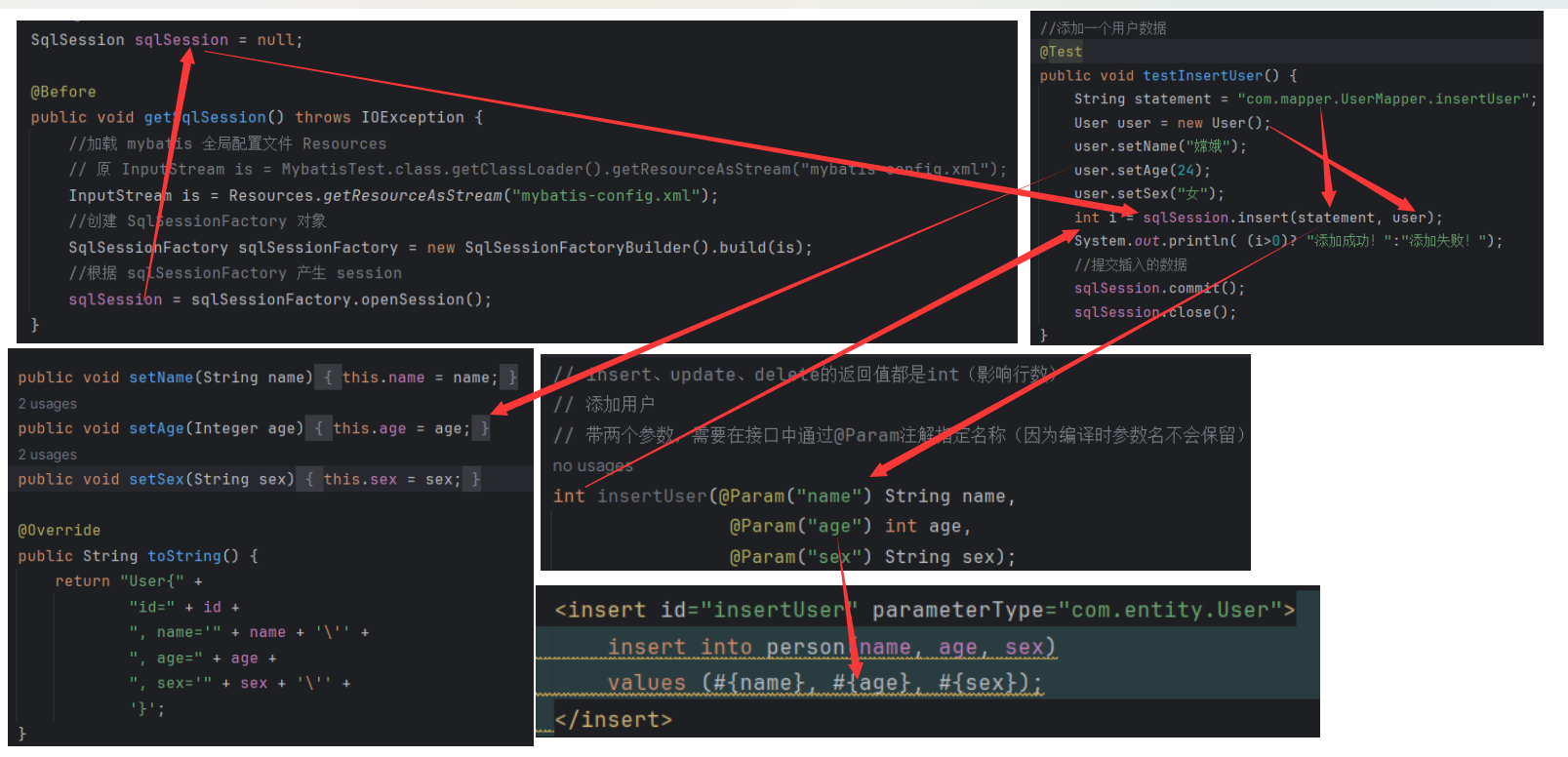
MyBatis 学习(二)之 第一个 MyBatis 案例
目录 1 配置 MyBatis 方式 1.1 XML 配置文件 1.2 Java 注解配置 1.3. Java API 配置 2 在 MySQL 中创建一张表 3 创建一个基于 Maven 的 JavaWeb 工程 4 编写 User 实体类 5 创建 Mybatis 全局配置文件 6 编写一个 DAO 或 Mapper 接口 7 编写 SQL 映射配置文件&#…...
)
30天自制操作系统(第21天)
21.1 攻克难题——字符串显示API 显示单个字符时,用 [CS:ECX] 的方式特意指定了 CS(代码段寄存器),因此可以成功读取 msg的内容。但在显示字符串时,由于无法指定段地址,程序误以为是 DS而从完全错误的内存地…...
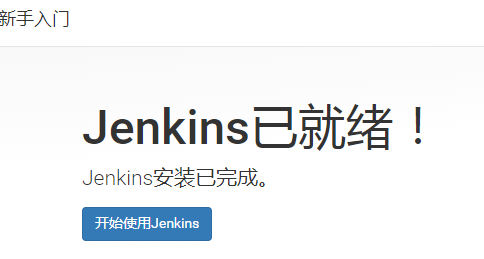
linux系统Jenkins的安装
Jenkins安装 安装上传安装包解压包首次登录要去服务器查看密码,更改密码选择需要安装的插件设置Admin用户和密码安装完成 安装 上传安装包 上传 jdk17 tomcat jenkins.war的安装包 . 上传 tomcat安装包解压包 解压jdk tar xf jdk-11.0.18_linux-x64_bin.tar.gz解…...

【GStreamer】basic-tutorial-1:GstBus、GstMessage详解
【目录】郭老二博文之:图像视频汇总 1、先看示例 #include <gst/gst.h>int main (int argc, char *argv[]) {GstElement *pipeline;GstBus...

Python中的可变变量与不可变变量
python中的可变与不可变变量 一、变量的三个参数 就像区分一个人一样,同样都是张三,可能这个张三就不是那个张三。同一个变量是指的什么相同呢? Python中的对象包含三个要素,id(内存地址),typ…...

OpenGL调用窗口,方向键和鼠标
9.2 OpenGL调用窗口,方向键和鼠标 9.2.1 opengl调用窗口 OpenGL调用窗口步骤: 第一步:初始化 GLFW,初始化OpenGL,初始化窗口,初始化上下文 第二步:设置窗口大小和位置,设置输入输出 第三步…...
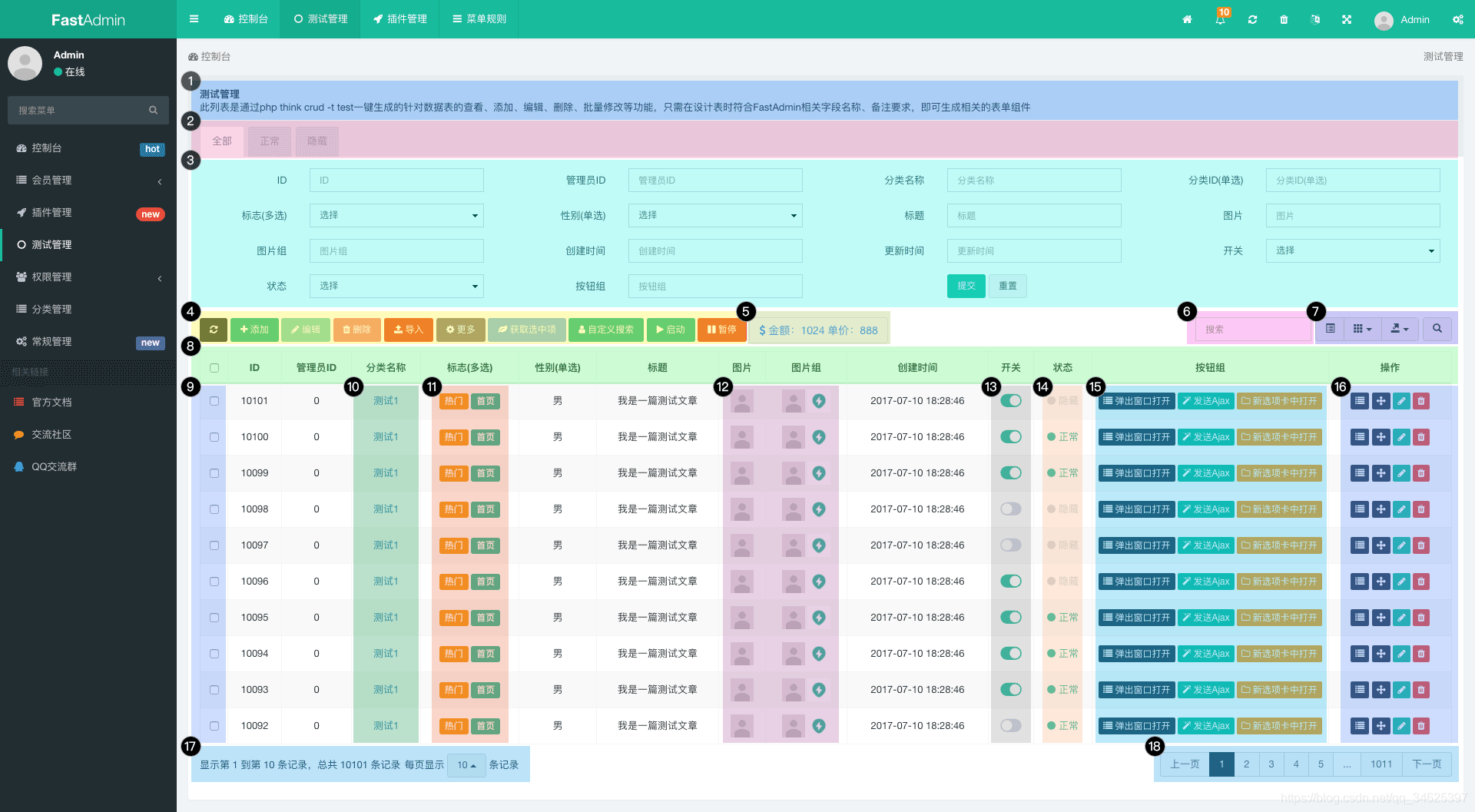
fastAdmin表格列表的功能
更多文章,请关注:fastAdmin后台功能详解 | 夜空中最亮的星 FastAdmin是一款基于ThinkPHP5Bootstrap的极速后台开发框架。优点见开发文档 介绍 - FastAdmin框架文档 - FastAdmin开发文档 在这里上传几张优秀的快速入门图: 一张图解析FastAdmin中的表格列…...

用来检查 CUDA、Conda 和 PyTorch 的版本的python文件
提供的 Python 代码片段包括几个语句,用来检查 CUDA、Conda 和 PyTorch 的版本,以及一些与 CUDA 相关的系统配置。让我们分解一下:PyTorch 版本和配置:torch.__config__.show():显示 PyTorch 的构建配置。 torch.__ver…...

基于Redisson,实现分布式锁注解
1.原始写法 我们平常使用redisson的分布式锁是不是基本都用下面的这个模板,既然是模板,那为何不把他抽出来呢? // 尝试加锁,最多等待100秒,上锁以后10秒自动解锁 boolean res lock.tryLock(100, 10, TimeUnit.SECON…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
