G. Special Permutation(构造)
1、题目
G. Special Permutation
这道题的意思是给我们从111到nnn的排列,然后我们对这个排列的顺序上进行调换,需要满足的条件是任意两个相邻元素的绝对值的差满足条件:2≤∣pi−pi+1∣≤42\leq |p_i-p_{i + 1}|\leq 42≤∣pi−pi+1∣≤4
2、分析
我们很容易发现,如果我们把奇数放在一起,偶数放在一起,那么对于这两部分而言,内部相邻的元素必定是满足条件的。
现在的问题是奇数部分和偶数部分之间衔接的地方,我们需要让这个地方也满足条件。因此,我们可以将奇数从大到小枚举,那么最后一
个奇数就一定是111。为了保证偶数和111的差值的绝对值是大于等于222的,我们就不能在111的右面放222。所以我们可以在111的右面放444。在444的右
面放222,222的后面放666。666后面按照升序枚举剩余的偶数即可。
根据上面的条件可以知道,我们必须得有444才行。所以如果我们的nnn是比444小,就无法构造出符合条件的序列,反之即可以构造。
3、代码
#include<bits/stdc++.h>
using namespace std;void solve()
{int n;cin >> n;vector<int>v(n);if(n < 4){cout << -1 << endl;return;}for(int i = n; i > 0; i --){if(i % 2)cout << i << " ";}cout << 4 << " ";for(int i = 2; i <= n; i ++ ){if(!(i % 2) && i != 4){cout << i << " ";}}cout << endl;return;
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);int t;cin >> t;while(t --)solve();
}
相关文章:
)
G. Special Permutation(构造)
1、题目 G. Special Permutation 这道题的意思是给我们从111到nnn的排列,然后我们对这个排列的顺序上进行调换,需要满足的条件是任意两个相邻元素的绝对值的差满足条件:2≤∣pi−pi1∣≤42\leq |p_i-p_{i 1}|\leq 42≤∣pi−pi1∣≤4 …...
QML动态对象管理
QML中有多种方式来动态创建和管理QML对象: Loader (加载器)Repeater(复制器)ListView,GridWiew,PethView(视图) (之后会介绍)使用加载器ÿ…...

cmake入门03 -自定义find外部库
自定义检测外部库使用pkg-config查找库搜索.pc配置文件cmake函数链接到库自定义find库检测外部库的便捷方法:使用CMake自带的find-module使用<package>Config.cmake, <package>ConfigVersion.cmake和<package>Targets.cmake。这些文件由软件商提供…...
Dubbo源码解析-——服务导出
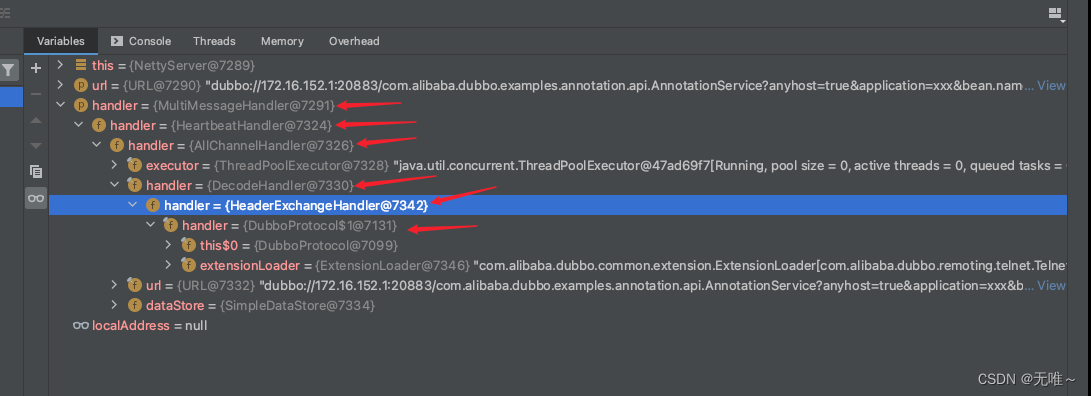
前言 在之前我们讲过Spring和Dubbo的集成,我们在服务上标注了DubboService的注解,然后最终Dubbo会调用到ServiceBean#export方法中,本次我们就来剖析下服务导出的全流程。 一、前置回顾 由于ServiceBean实现了ApplicationListener接口&…...

vue+django+neo4j 基于知识图谱红楼梦问答系统
vuedjangoneo4j 基于知识图谱红楼梦问答系统 项目背景 知识图谱是一种以图谱形式描述客观世界中存在的各种实体、概念及其关系的技术, 广泛应用于智能搜索、自动问答和决策支持等领域. 可视分析技术可以将抽象的知识图谱映射为图形元素, 帮助用户直观地感知和分析数据, 从而提…...

2023年全国最新食品安全管理员精选真题及答案13
百分百题库提供食品安全管理员考试试题、食品安全员考试预测题、食品安全管理员考试真题、食品安全员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 121.关于食品召回的说法,以下表述不正确的是(&am…...

Keychron K7 Pro 轻薄矮轴机械键盘开箱体验
文章目录1. 拆箱2. 零件3. 外观4. 声音5. 特点5.1 有线 / 无线5.2 RGB背光5.3 轻薄5.4 mac / win / iphone 切换5.5 人体工程学支持5.6 扁平双射PBT键帽5.7 重新设计的稳定器5.8 扁平Gateron(佳达隆)轴体5.9 热插拔5.10 支持 QMK / VIA 改键6. 对比6.1 K7 与 K7 Pro 参数对比6.…...
加油站ai视觉识别系统 yolov7
加油站ai视觉识别系统通过yolov7网络模型深度学习,加油站ai视觉识别算法对现场画面中人员打电话抽烟等违规行为,还有现场出现明火烟雾等危险状态。除此之外,模型算法还可以对卸油时灭火器未正确摆放、人员离岗不在现场、卸油过程静电释放时间…...
【电子学会】2022年12月图形化二级 -- 绘制风车
绘制风车 1. 准备工作 (1)隐藏默认的小猫角色; (2)选择背景:“Xy-grid”。 2. 功能实现 (1)小猫角色的初始位置为(x:0,y:0); (2)线条粗细为…...

【golang/go语言】Go语言代码实践——高复用、易扩展性代码训练
某个项目里有一段老代码写的不是很好,想着能否通过自己掌握的知识,将其改善一下。感兴趣的小伙伴可以通过了解背景和需求,自己试想下该如何实现,如果有更好的方案也欢迎留言讨论。 1. 背景及需求 (1) 背景 假设我们的下游提供了…...
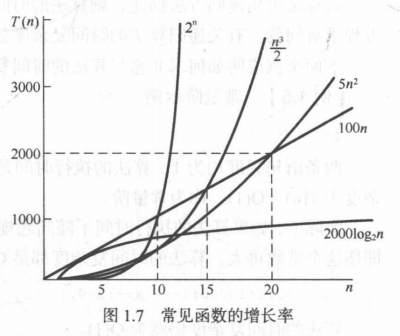
[数据结构与算法(严蔚敏 C语言第二版)]第1章 绪论(学习复习笔记)
1.1 数据结构的研究内容 计算机解决问题的步骤 从具体问题抽象出数学模型设计一个解此数学模型的算法编写程序,进行测试、调试,直到解决问题 计算机解决问题的过程中寻求数学模型的实质是 分析问题,从中提取操作的对象,并找出这些…...

05_Pulsar的主要组件介绍与命令使用、名称空间、Pulsar的topic相关操作、Pulsar Topic(主题)相关操作_高级操作、
1.5.Apache Pulsar的主要组件介绍与命令使用 1.5.1.多租户模式 1.5.1.1. 什么是多租户 1.5.1.2.Pulsar多租户的相关特征_安全性(认证和授权) 1.5.1.3.Pulsar多租户的相关特性_隔离性 1.5.1.4.Pulsar多租户的相关操作 1-获取租户列表 2-创建租户 3-获取配…...

我的终端怎么莫名卡死了?shell下ctrl+s的含义
在终端下面一不小心按下了ctrl s,整个终端就锁住了,不知道原油的同学可能会以为终端卡死了,找不到原因只好关闭终端重新打开,然后下意识还不忘吐槽一句,垃圾ubuntu,动不动卡死。 事实上ctrl s在终端下是…...
【Vue】Vue的简单介绍与基本使用
一、什么是VueVue是一款用于构建用户界面的 JavaScript 框架。它基于标准 HTML、CSS 和 JavaScript 构建,并提供了一套声明式的、组件化的编程模型,帮助你高效地开发用户界面。无论是简单还是复杂的界面,Vue 都可以胜任。1.构建用户界面传统方…...

网络知识篇
网络知识篇 局域网 当多台计算机或设备通过同一物理或逻辑连接(例如以太网或Wi-Fi网络)连接在一起,并且它们可以相互通信时,就构成了一个局域网(Local Area Network,LAN)。 子网划分 为了更…...
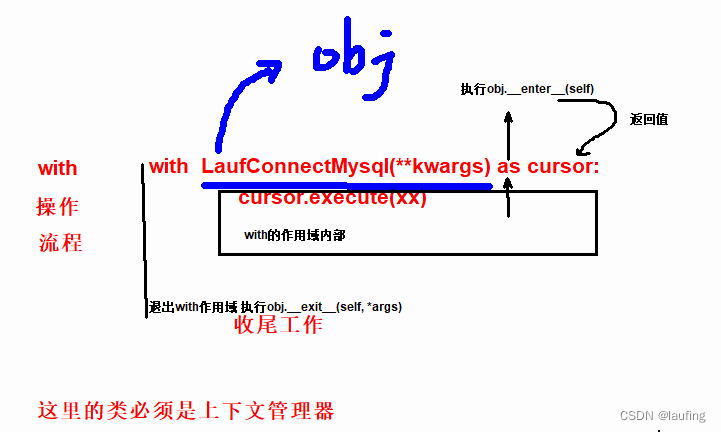
python 连接数据库
文章目录同步操作同步连Mysql同步连redis同步连mongodb异步操作异步连mysql异步连redis异步连mongodb同步操作 同步连Mysql python 连接mysql可以使用pymysql、mysqlclient等。 安装: # win pip install pymysql 连接mysql: # __author__ "laufing"…...

一文讲明白一致性hash算法
一致性Hash算法常用来解决数据分片时的数据扩容/缩容的性能问题。 一、业内数据分片用的Hash算法,将节点的hash值对节点数取余。 存取通过key / value的方式对节点取余。 二、数据分片使用hash算法的优缺点: 优点:简单,方便。 缺…...

Java分布式解决方案(一)
随着互联网的不断发展,互联网企业的业务在飞速变化,推动着系统架构也在不断地发生变化。 如今微服务技术越来越成熟,很多企业都采用微服务架构来支撑内部及对外的业务,尤其是在高 并发大流量的电商业务场景下,微服务…...
设备树的节点和属性)
设备树系统学习(二)设备树的节点和属性
一、节点 1.节点命名格式 格式:<name>[@<unit-address>] name:是一个简单的 ASCII 字符串,长度最多为 31 个字符,节节点是根据它所代表的设备类型来命名的,比如 “gpu” 就表示这个节点是 gpu外设。 unit-address:一般表示设备的地址或寄存器首地址,可以为…...

【数据结构】二叉树的基本操作中的一些易错点
文章目录前言一、求二叉树节点个数二、求树的叶子结点个数三、求树的高度四、二叉树查找值为x的结点总结前言 笔者整理出了一些关于萌新在入门二叉树时容易犯的一些错误,你也来试试自己会不会掉到这些坑里把~ 一、求二叉树节点个数 错误示例: int Tre…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
)
LLaMA-Factory 微调 Qwen2-VL 进行人脸情感识别(二)
在上一篇文章中,我们详细介绍了如何使用LLaMA-Factory框架对Qwen2-VL大模型进行微调,以实现人脸情感识别的功能。本篇文章将聚焦于微调完成后,如何调用这个模型进行人脸情感识别的具体代码实现,包括详细的步骤和注释。 模型调用步骤 环境准备:确保安装了必要的Python库。…...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...
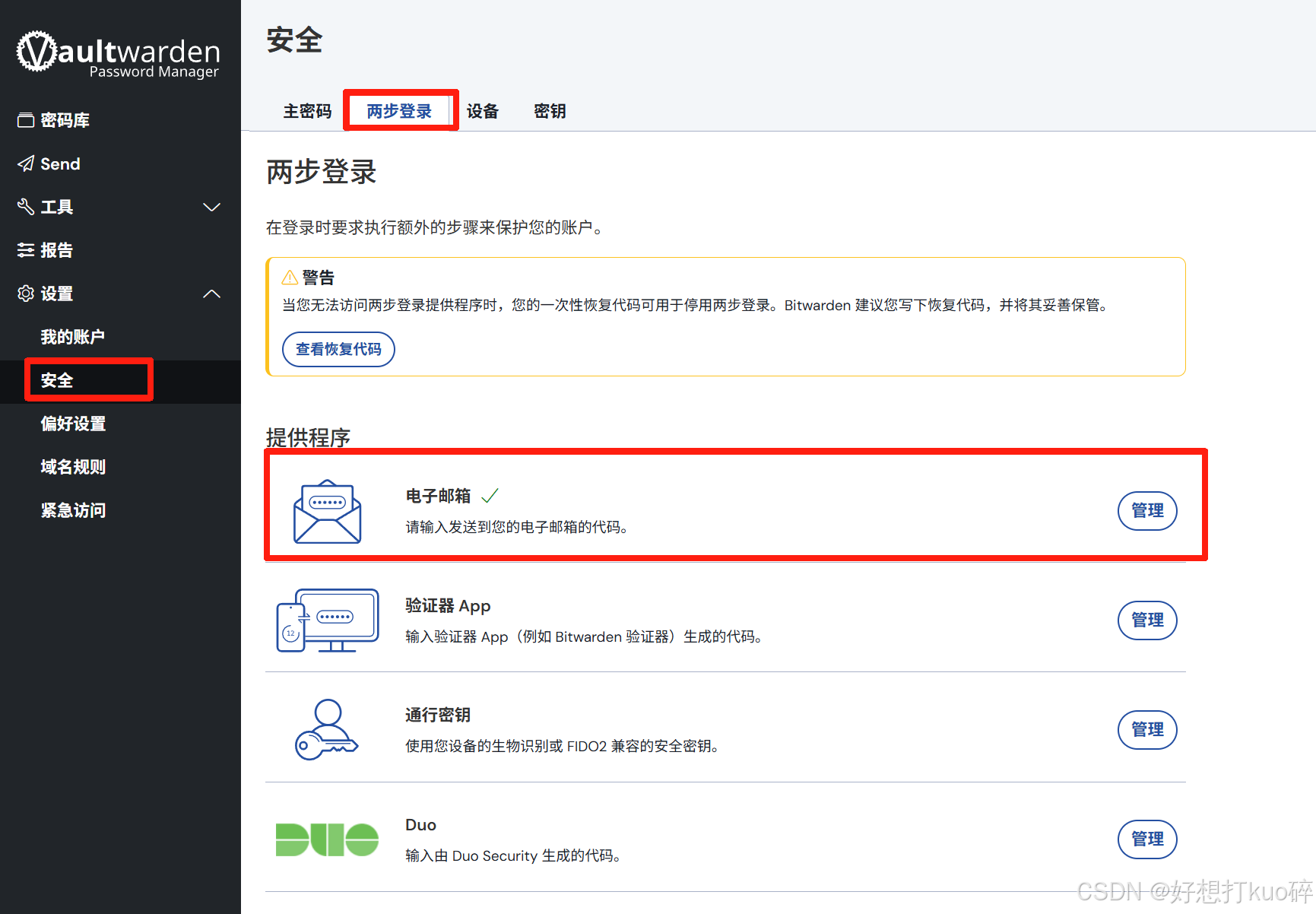
轻量安全的密码管理工具Vaultwarden
一、Vaultwarden概述 Vaultwarden主要作用是提供一个自托管的密码管理器服务。它是Bitwarden密码管理器的第三方轻量版,由国外开发者在Bitwarden的基础上,采用Rust语言重写而成。 (一)Vaultwarden镜像的作用及特点 轻量级与高性…...
