贝叶斯分类器
贝叶斯分类器
1. 引言
贝叶斯分类器是一种基于贝叶斯定理的分类算法,它利用特征之间的关系和类别的先验概率来进行分类。贝叶斯分类器在文本分类、垃圾邮件过滤、医学诊断等领域有着广泛的应用。
贝叶斯分类算法是统计学的一种分类方法,是一类利用概率统计知识进行分类的方法。这类算法均以贝叶斯定理为基础,统称为贝叶斯分类。贝叶斯的核心思想为可以概括为:先验概率+数据=后验概率。(一般而言,先验概率就是对于数据所在领域的历史经验,贝叶斯学派大胆假设先验分布的模型,如正态分布、伯努利分布等)
在所有的机器学习分类算法当中,朴素贝叶斯和其他绝大多数的分类算法不同。对于大多数的分类算法,比如决策树、逻辑回归、支持向量机等,他们都是判别方法,也就是直接学习出特征输出Y和特征X之间的关系,要么是决策函数 Y = f ( X ) Y=f(X) Y=f(X),要么是条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X),但是朴素贝叶斯是生成方法,也就是直接找出特征输出Y和特征X之间的联合分布 P ( X , Y ) P(X, Y) P(X,Y),然后利用 P ( Y ∣ X ) = P ( X , Y ) P ( X ) P(Y|X) = \frac{P(X,Y)}{P(X)} P(Y∣X)=P(X)P(X,Y)得到。
2. 预备知识
为了理解贝叶斯分类器,我们需要了解一些基本的概念:
- 贝叶斯定理:用于计算在观测到数据后,类别的后验概率。
- 先验概率:在观测到数据之前,对类别的概率分布的估计。
- 条件概率:在给定某个条件下,某个事件发生的概率。
2.1 贝叶斯定理
贝叶斯定理是一个关于条件概率的公式,又称为“逆概率”或“后验概率”。它表述了当我们已知某个条件下的观察结果时,我们可以利用这些信息来更新对一个假设的概率估计。其公式为:
P ( H ∣ E ) = P ( E ∣ H ) P ( H ) P ( E ) P(H|E) = \frac{P(E|H)P(H)}{P(E)} P(H∣E)=P(E)P(E∣H)P(H)
其中, P ( H ∣ E ) P(H|E) P(H∣E)表示在发生E的情况下, H H H发生的概率; P ( E ∣ H ) P(E|H) P(E∣H)表示在发生H的情况下,E发生的概率; P ( H ) P(H) P(H)表示H发生的先验概率, P ( E ) P(E) P(E)表示E发生的概率。
2.2 最大似然估计
最大似然估计(Maximum Likelihood Estimation, MLE),也称为极大似然估计,是用来估计概率模型参数的一种方法。它可以在已知随机变量属于某种概率分布的前提下,利用随机变量的一些观测值估计出分布的参数值。
对于函数 p ( x ∣ θ ) p(x|\theta) p(x∣θ),输入有两个: x x x表示某个具体数据, θ \theta θ表示模型的参数。
- 如果 θ \theta θ已知, x x x是变量,则该函数称为概率函数(probability function),描述对于不同的样本点 x x x,其出现的概率是多少;
- 如果 x x x已知, θ \theta θ是变量,该函数称为似然函数(likelihood function),描述对于不同的模型参数,出现 x x x这个样本点的概率是多少。
极大似然估计假设样本集中的所有样本都是独立同分布的,样本集合为 D D D,以此来估计参数向量 θ \theta θ。记已知的样本集为: D = x 1 , x 2 , . . . , x N D={x_1, x_2, ..., x_N} D=x1,x2,...,xN。
似然函数(likelihood function):联合概率密度函数 p ( D ∣ θ ) p(D|\theta) p(D∣θ)称为 D = { x 1 , . . . , x N } D=\{x_1, ..., x_N\} D={x1,...,xN}关于 θ \theta θ的似然函数。
L ( θ ) = p ( D ∣ θ ) = p ( x 1 , . . . , x N ∣ θ ) = ∏ i = 1 N p ( x i ∣ θ ) L(\theta) = p(D|\theta)=p(x_1,...,x_N|\theta)=\prod_{i=1}^N p(x_i|\theta) L(θ)=p(D∣θ)=p(x1,...,xN∣θ)=i=1∏Np(xi∣θ)
值得注意的是,这里的 p ( x 1 , . . . , x N ∣ θ ) = ∏ i = 1 N p ( x i ∣ θ ) p(x_1,...,x_N|\theta)=\prod_{i=1}^N p(x_i|\theta) p(x1,...,xN∣θ)=∏i=1Np(xi∣θ)的前提是属性之间相互独立,这是朴素贝叶斯所作出的假设。
3. 算法介绍
贝叶斯分类器模型表述为
P ( c ∣ x ) = P ( x , c ) P ( x ) P(c|x)=\frac{P(x,c)}{P(x)} P(c∣x)=P(x)P(x,c)
基于贝叶斯定理, P ( c ∣ x ) P(c|x) P(c∣x)可写为
P ( c ∣ x ) = P ( c ) P ( x ∣ c ) P ( x ) P(c|x)=\frac{P(c)P(x|c)}{P(x)} P(c∣x)=P(x)P(c)P(x∣c)
其中, P ( c ) P(c) P(c)是类“先验”概率, P ( x ∣ c ) P(x|c) P(x∣c)是样本 x x x相对于类标记c的类条件概率,或者称之为“似然”;对于每个类别来说,分母都是相同的,因而在求解时可以只比较分子部分。
朴素贝叶斯模型的关键在于计算给定样本时的每个类别的后验概率,后验概率最大的类别即为输出类别。
令 D c D_c Dc表示训练集 D D D中第c个类别样本组成的集合,假设这些样本是独立同分布的,则参数 θ c \theta_c θc对于数据集 D c D_c Dc的似然是
P ( D c ∣ θ c ) = ∏ x ∈ D c P ( x ∣ θ c ) P(D_c|\theta_c)=\prod _{x\in D_c}P(x|\theta_c) P(Dc∣θc)=x∈Dc∏P(x∣θc)
对 θ c \theta_c θc进行极大似然估计,就是去寻找能够最大化似然 P ( D c ∣ θ c ) P(D_c|\theta_c) P(Dc∣θc)的参数值 θ c ^ \hat{\theta_c} θc^,直观上看,极大似然估计是试图在 θ c \theta_c θc的所有可能取值中,找到一个能够使得数据出现的“可能性”最大的值,也即
θ c ^ = a r g m a x θ c P ( D c ∣ θ c ) \hat{\theta_c} = argmax_{\theta_c}P(D_c|\theta_c) θc^=argmaxθcP(Dc∣θc)
估计类条件概率的一种常用策略是先假定其具有某种确定的概率分布形式,再根据训练样本对概率分布的参数进行估计。
在连续属性的情形下,假设概率密度函数 p ( x ∣ c ) ∼ N ( μ c , σ c 2 ) p(x|_c)\sim N(\mu_c, \sigma_c^2) p(x∣c)∼N(μc,σc2),则参数 μ c \mu_c μc和 σ c 2 \sigma_c^2 σc2的极大似然估计为
μ c ^ = 1 D c ∑ x ∈ D c x σ c 2 ^ = 1 D c ∑ x ∈ D c ( x − μ c ^ ) ( x − μ c ^ ) T \hat{\mu_c} = \frac{1}{D_c}\sum_{x\in D_c}x \\ \hat{\sigma_c^2} = \frac{1}{D_c}\sum_{x\in D_c}(x-\hat{\mu_c})(x-\hat{\mu_c}) ^T μc^=Dc1x∈Dc∑xσc2^=Dc1x∈Dc∑(x−μc^)(x−μc^)T
也就是说,通过极大似然法得到的正态分布均值就是样本均值,方差就是 ( x − μ c ^ ) ( x − μ c ^ ) T (x-\hat{\mu_c})(x-\hat{\mu_c}) ^T (x−μc^)(x−μc^)T的均值。
归纳为步骤:
- 计算每个类别的先验概率。
- 对于每个特征,计算在给定类别的条件下的类条件概率。
- 根据贝叶斯定理计算后验概率。
- 根据后验概率选择类别。
4. 代码调用
下面是一个简单的Python代码实现贝叶斯分类器的示例:
from sklearn.naive_bayes import GaussianNB
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score# 加载数据集
data = load_iris()
X = data.data
y = data.target# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)# 创建贝叶斯分类器模型
model = GaussianNB()# 在训练集上训练模型
model.fit(X_train, y_train)# 在测试集上进行预测
y_pred = model.predict(X_test)# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)参考文献
- https://mp.weixin.qq.com/s/AQnMNOJznAbnTy5QnALaCw
- https://blog.csdn.net/yinyu19950811/article/details/78060267
- 周志华《机器学习》
相关文章:

贝叶斯分类器
贝叶斯分类器 1. 引言 贝叶斯分类器是一种基于贝叶斯定理的分类算法,它利用特征之间的关系和类别的先验概率来进行分类。贝叶斯分类器在文本分类、垃圾邮件过滤、医学诊断等领域有着广泛的应用。 贝叶斯分类算法是统计学的一种分类方法,是一类利用概率…...

游戏服务之会话管理
会话的概念与作用 游戏服务器 Session(会话)是指在游戏服务器和客户端之间建立的一个临时的连接。它可以用于存储和管理用户的游戏状态和信息。 当用户登录游戏时,服务器会为该用户创建一个 Session,可用于记录用户的登录状态、角色信息等个人信息。服务器会为每个会话分…...

LeetCode20 有效的括号
题目 给定一个只包括 (,),{,},[,] 的字符串 s ,判断字符串是否有效。有效字符串需满足:1、左括号必须用相同类型的右括号闭合。 2、左括号必须以正确的顺序闭合。 3、每个右括号都有一个对应的相…...

sql实战_基于某推荐比值问题
将一个月内某PL对应的MBLX出现的最高的频次的占比值最大的值统计出来,并且还要把XHLX,MBLX字段添加上作为最终的推荐字段 Select * from(select *,row_number( ) over (partition by PL order by 占比最大值 desc ) rn from 表) where rn 1;…...
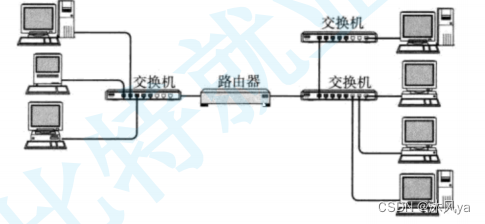
协议的概念+本质+作用+最终表现形式,网络问题(技术+应用+解决的协议+存在原因),主机的对称性
目录 协议 概念 示例 -- 摩斯密码 介绍 作用 协议的本质 作用 网络问题 引入 技术问题 应用问题 主机的对称性 问题对应的协议 问题出现的原因 理解协议(代码层面) 举例 -- 快递单 协议的最终表现形式 协议被双方主机认知的基础 协议 概念 协议是在计算机通信…...
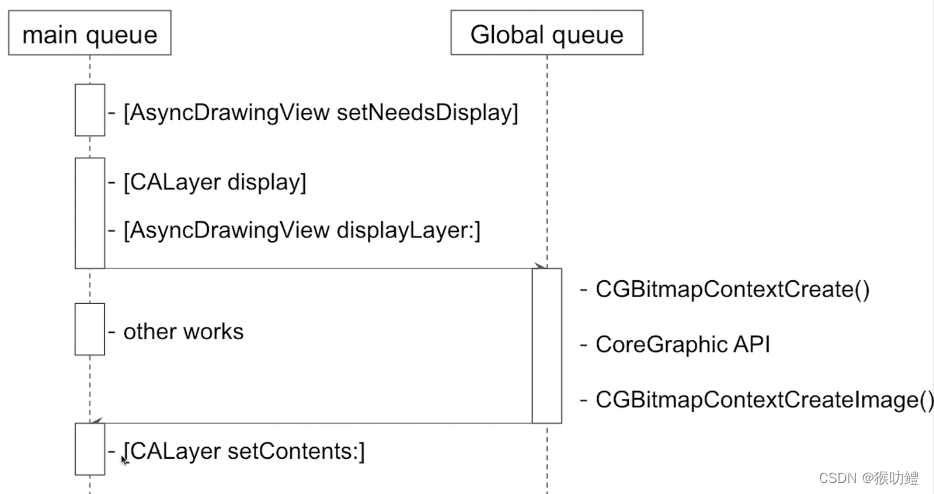
iOS中卡顿产生的主要原因及优化思路
卡顿本质上是一个UI体验上的问题,而UI的渲染及显示,主要涉及CPU和GPU两个层面。若 CPUGPU渲染耗时超过16.7ms,就会在屏幕vsync信号到来时无法更新屏幕内容,进而导致卡顿。 iOS中UI渲染主要包含Layout->Draw->Prepare->Co…...
spring boot集成Elasticsearch 7.16.3
环境:Elasticsearch 版本 7.16.3 Elasticsearch for windows下载地址 windows 若依 spring boot版本 2.6.0 pom文件添加 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-elasticsearch<…...

HTML5+CSS3小实例:环绕小球弹性loading动画
实例:环绕小球弹性loading动画 技术栈:HTML+CSS 效果: 源码: 【HTML】 <!DOCTYPE html> <html lang="zh-CN"><head><meta charset="UTF-8" /><meta http-equiv="X-UA-Compatible" content="IE=edge&quo…...
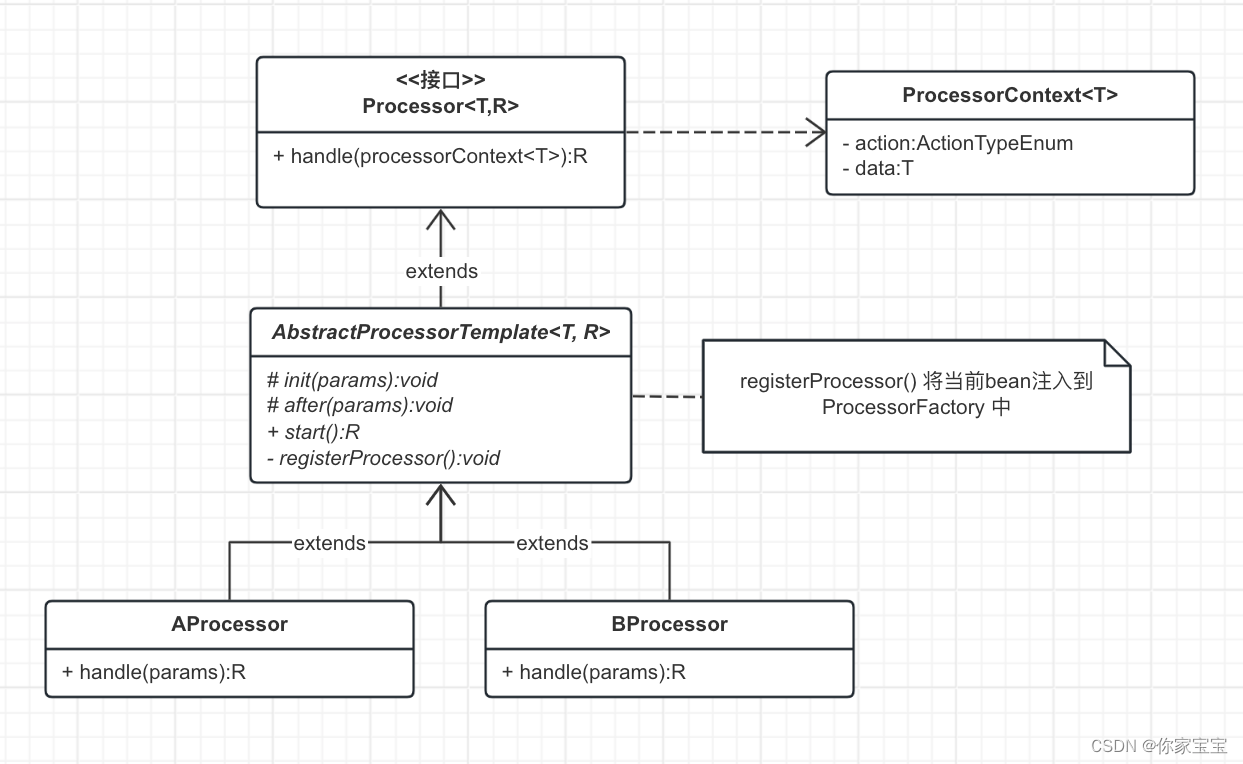
SpringBoot 自定义注解实现操作日志记录
文章目录 前言正文一、项目结构介绍二、核心类2.1 核心注解2.1.1 CLog 日志注解2.1.2 ProcessorBean 处理器bean 2.2 切面类2.3 自定义线程池2.4 工具类2.4.1 管理者工具类 2.5 测试2.5.1 订单创建处理器2.5.2 订单管理者2.5.3 订单控制器2.5.4 测试报文2.5.5 测试结果 附录1、…...

ubuntu常见配置
ubuntu各个版本的安装过程大差小不差,可以参考,ubuntu20.04 其它版本换一下镜像版本即可 安装之后需要配置基本的环境,我的话大概就以下内容,后续可能有所删改 sudo apt-get update sudo apt-get install gcc sudo apt-get inst…...
electron+vue3全家桶+vite项目搭建【27】封装窗口工具类【1】雏形
文章目录 引入思路抽出公共声明文件抽出全局通用数据类型和方法主进程模块1.抽离基础常量2.封装窗口工具类 渲染进程模块测试结果 引入 demo项目地址 可以看到我们之前在主进程中的逻辑全部都塞到index.ts文件中,包括窗口的一些事件处理,handle监听&am…...
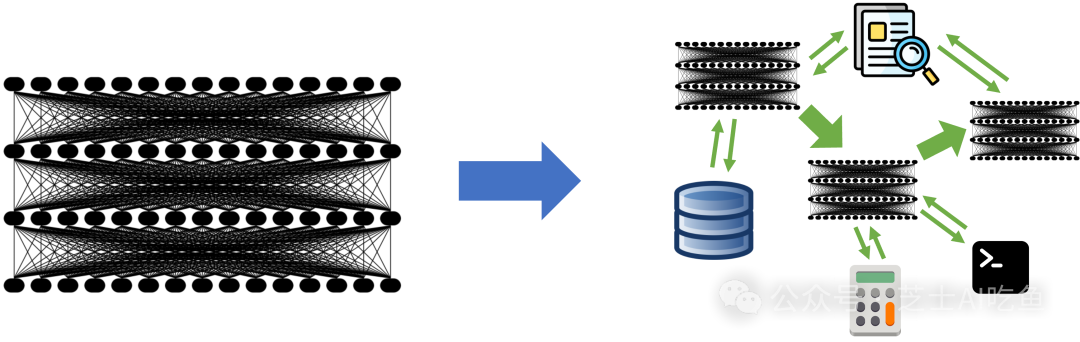
从模型到复合AI系统的转变
2023年,大型语言模型(LLM)吸引了所有人的注意力,它可以通过提示来执行通用任务,例如翻译或编码。这自然导致人们将模型作为AI应用开发的主要成分而密切关注,所有人都在想新的LLM将带来什么能力。然而,随着越来越多的开发者开始使用LLM构建,我们认为这种关注正在迅速改变:最先进…...

将仓库A中的部分提交迁移到仓库B中
结论: 使用git format-patchgit am即可实现 使用场景: 例如仓库A这里有5个提交记录,commitid1, commitid2, commitid3, commitid4,commitid5 仓库B想用仓库A中提交的代码,手动改比较慢,当改动较多的时候…...

信息安全技术基础
本博客地址:https://security.blog.csdn.net/article/details/136331705 一、信息安全基础 1、信息安全的基本要素有机密性、完整性、可用性、可控性与可审查性。信息安全的范围包括设备安全、数据安全、内容安全和行为安全。其中数据安全即采取措施确保数据免受未…...
flask知识--01
flask介绍 # python 界的web框架: Django:大而全,使用率较高 :https://github.com/django/django -FastAPI:新项目选择使用它:https://github.com/tiangolo/fastapi -flask:公司一些…...

软考52-上午题-【数据库】-关系模式2
一、关系模式的回顾 见:软考38-上午题-【数据库】-关系模式 二、关系模式 2-1、关系模式的定义 示例: 念法:A——>B A决定B,或者,B依赖于A。 2-2、函数依赖 1、非平凡的函数依赖 如果X——>Y,&a…...

devc++跑酷小游戏3.5.0
本来想搞存档的,失败了,要再学学文件操作的函数。还有一个打印地图的函数,更失败,彻底放弃。最近开学了,游戏不会经常更新,要写作业。昨天写到10点T_T #include<bits/stdc.h> #include<windows.h…...

Redisson限流算法
引入依赖 <dependency><groupId>org.redisson</groupId><artifactId>redisson-spring-boot-starter</artifactId><version>3.12.3</version> </dependency>建议版本使用3.15.5以上 使用 这边写了一个demo示例,定…...

GPT与MBR:硬盘分区表格式的革新与区别
概述 在计算机存储领域,硬盘分区是管理数据和操作系统部署的基础。两种广泛使用的分区表格式——MBR(Master Boot Record)和GPT(GUID Partition Table),各自代表了不同的技术阶段和发展需求。本文将详细介…...

机器学习-1
文章目录 前言机器学习基本定义 练习题 前言 在本片开始将为大家介绍机器学习相关的知识点。 机器学习基本定义 夏天,我们通常会去水果店里买西瓜,我们看到一个根蒂蜷缩、敲起来声音浑浊的青绿色的西瓜,我们提着西瓜就去结账了,…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
