LeetCode每日一题2673. Make Costs of Paths Equal in a Binary Tree
文章目录
- 一、题目
- 二、题解
一、题目
You are given an integer n representing the number of nodes in a perfect binary tree consisting of nodes numbered from 1 to n. The root of the tree is node 1 and each node i in the tree has two children where the left child is the node 2 * i and the right child is 2 * i + 1.
Each node in the tree also has a cost represented by a given 0-indexed integer array cost of size n where cost[i] is the cost of node i + 1. You are allowed to increment the cost of any node by 1 any number of times.
Return the minimum number of increments you need to make the cost of paths from the root to each leaf node equal.
Note:
A perfect binary tree is a tree where each node, except the leaf nodes, has exactly 2 children.
The cost of a path is the sum of costs of nodes in the path.
Example 1:
Input: n = 7, cost = [1,5,2,2,3,3,1]
Output: 6
Explanation: We can do the following increments:
- Increase the cost of node 4 one time.
- Increase the cost of node 3 three times.
- Increase the cost of node 7 two times.
Each path from the root to a leaf will have a total cost of 9.
The total increments we did is 1 + 3 + 2 = 6.
It can be shown that this is the minimum answer we can achieve.
Example 2:
Input: n = 3, cost = [5,3,3]
Output: 0
Explanation: The two paths already have equal total costs, so no increments are needed.
Constraints:
3 <= n <= 105
n + 1 is a power of 2
cost.length == n
1 <= cost[i] <= 104
二、题解
class Solution {
public:int minIncrements(int n, vector<int>& cost) {int res = 0;for(int i = n / 2;i > 0;i--){res += abs(cost[i * 2 - 1] - cost[i * 2]);cost[i - 1] += max(cost[i * 2 - 1],cost[i * 2]);}return res;}
};
相关文章:

LeetCode每日一题2673. Make Costs of Paths Equal in a Binary Tree
文章目录 一、题目二、题解 一、题目 You are given an integer n representing the number of nodes in a perfect binary tree consisting of nodes numbered from 1 to n. The root of the tree is node 1 and each node i in the tree has two children where the left ch…...

贝叶斯分类器
贝叶斯分类器 1. 引言 贝叶斯分类器是一种基于贝叶斯定理的分类算法,它利用特征之间的关系和类别的先验概率来进行分类。贝叶斯分类器在文本分类、垃圾邮件过滤、医学诊断等领域有着广泛的应用。 贝叶斯分类算法是统计学的一种分类方法,是一类利用概率…...

游戏服务之会话管理
会话的概念与作用 游戏服务器 Session(会话)是指在游戏服务器和客户端之间建立的一个临时的连接。它可以用于存储和管理用户的游戏状态和信息。 当用户登录游戏时,服务器会为该用户创建一个 Session,可用于记录用户的登录状态、角色信息等个人信息。服务器会为每个会话分…...

LeetCode20 有效的括号
题目 给定一个只包括 (,),{,},[,] 的字符串 s ,判断字符串是否有效。有效字符串需满足:1、左括号必须用相同类型的右括号闭合。 2、左括号必须以正确的顺序闭合。 3、每个右括号都有一个对应的相…...

sql实战_基于某推荐比值问题
将一个月内某PL对应的MBLX出现的最高的频次的占比值最大的值统计出来,并且还要把XHLX,MBLX字段添加上作为最终的推荐字段 Select * from(select *,row_number( ) over (partition by PL order by 占比最大值 desc ) rn from 表) where rn 1;…...
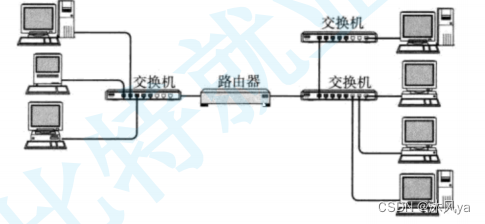
协议的概念+本质+作用+最终表现形式,网络问题(技术+应用+解决的协议+存在原因),主机的对称性
目录 协议 概念 示例 -- 摩斯密码 介绍 作用 协议的本质 作用 网络问题 引入 技术问题 应用问题 主机的对称性 问题对应的协议 问题出现的原因 理解协议(代码层面) 举例 -- 快递单 协议的最终表现形式 协议被双方主机认知的基础 协议 概念 协议是在计算机通信…...
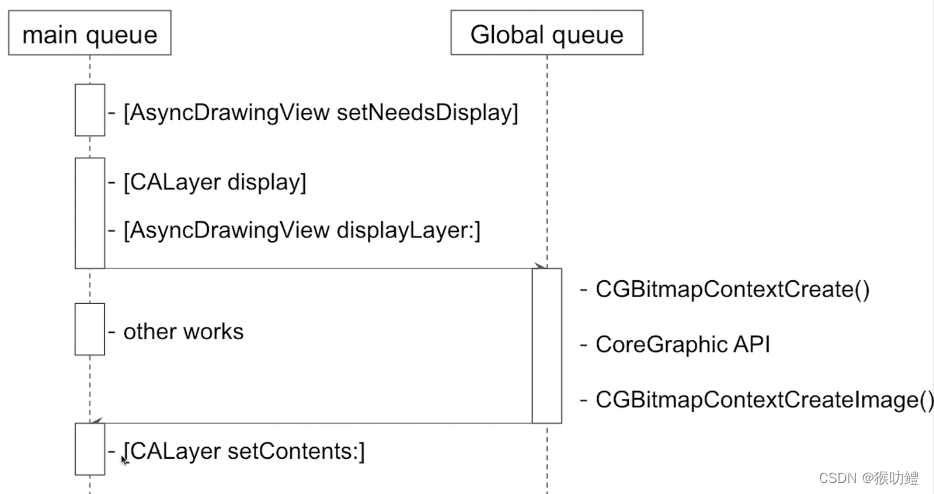
iOS中卡顿产生的主要原因及优化思路
卡顿本质上是一个UI体验上的问题,而UI的渲染及显示,主要涉及CPU和GPU两个层面。若 CPUGPU渲染耗时超过16.7ms,就会在屏幕vsync信号到来时无法更新屏幕内容,进而导致卡顿。 iOS中UI渲染主要包含Layout->Draw->Prepare->Co…...
spring boot集成Elasticsearch 7.16.3
环境:Elasticsearch 版本 7.16.3 Elasticsearch for windows下载地址 windows 若依 spring boot版本 2.6.0 pom文件添加 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-elasticsearch<…...

HTML5+CSS3小实例:环绕小球弹性loading动画
实例:环绕小球弹性loading动画 技术栈:HTML+CSS 效果: 源码: 【HTML】 <!DOCTYPE html> <html lang="zh-CN"><head><meta charset="UTF-8" /><meta http-equiv="X-UA-Compatible" content="IE=edge&quo…...
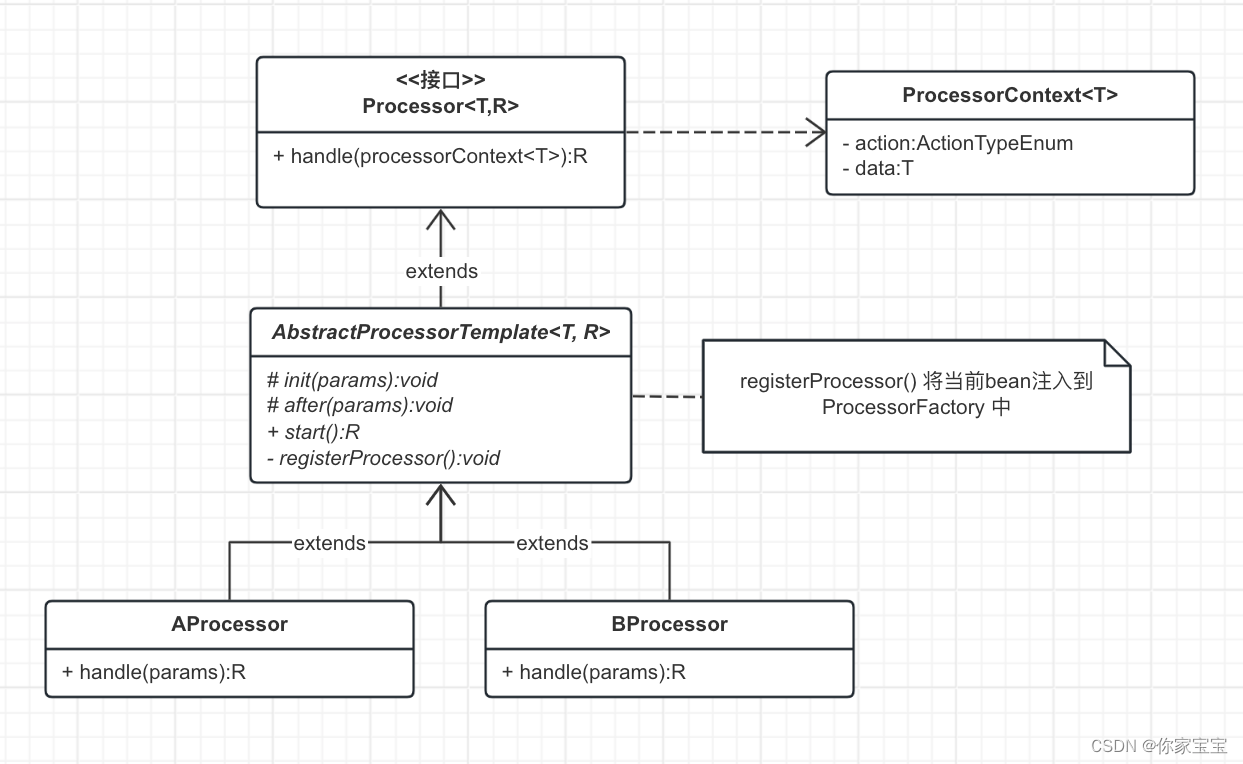
SpringBoot 自定义注解实现操作日志记录
文章目录 前言正文一、项目结构介绍二、核心类2.1 核心注解2.1.1 CLog 日志注解2.1.2 ProcessorBean 处理器bean 2.2 切面类2.3 自定义线程池2.4 工具类2.4.1 管理者工具类 2.5 测试2.5.1 订单创建处理器2.5.2 订单管理者2.5.3 订单控制器2.5.4 测试报文2.5.5 测试结果 附录1、…...

ubuntu常见配置
ubuntu各个版本的安装过程大差小不差,可以参考,ubuntu20.04 其它版本换一下镜像版本即可 安装之后需要配置基本的环境,我的话大概就以下内容,后续可能有所删改 sudo apt-get update sudo apt-get install gcc sudo apt-get inst…...
electron+vue3全家桶+vite项目搭建【27】封装窗口工具类【1】雏形
文章目录 引入思路抽出公共声明文件抽出全局通用数据类型和方法主进程模块1.抽离基础常量2.封装窗口工具类 渲染进程模块测试结果 引入 demo项目地址 可以看到我们之前在主进程中的逻辑全部都塞到index.ts文件中,包括窗口的一些事件处理,handle监听&am…...
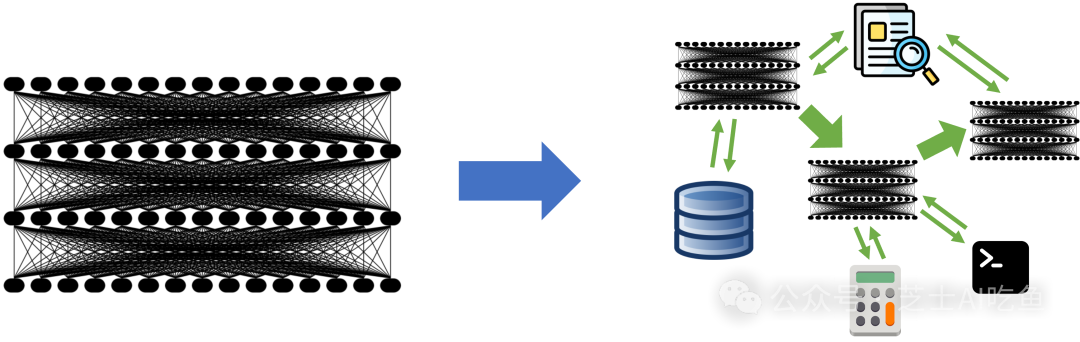
从模型到复合AI系统的转变
2023年,大型语言模型(LLM)吸引了所有人的注意力,它可以通过提示来执行通用任务,例如翻译或编码。这自然导致人们将模型作为AI应用开发的主要成分而密切关注,所有人都在想新的LLM将带来什么能力。然而,随着越来越多的开发者开始使用LLM构建,我们认为这种关注正在迅速改变:最先进…...

将仓库A中的部分提交迁移到仓库B中
结论: 使用git format-patchgit am即可实现 使用场景: 例如仓库A这里有5个提交记录,commitid1, commitid2, commitid3, commitid4,commitid5 仓库B想用仓库A中提交的代码,手动改比较慢,当改动较多的时候…...

信息安全技术基础
本博客地址:https://security.blog.csdn.net/article/details/136331705 一、信息安全基础 1、信息安全的基本要素有机密性、完整性、可用性、可控性与可审查性。信息安全的范围包括设备安全、数据安全、内容安全和行为安全。其中数据安全即采取措施确保数据免受未…...
flask知识--01
flask介绍 # python 界的web框架: Django:大而全,使用率较高 :https://github.com/django/django -FastAPI:新项目选择使用它:https://github.com/tiangolo/fastapi -flask:公司一些…...

软考52-上午题-【数据库】-关系模式2
一、关系模式的回顾 见:软考38-上午题-【数据库】-关系模式 二、关系模式 2-1、关系模式的定义 示例: 念法:A——>B A决定B,或者,B依赖于A。 2-2、函数依赖 1、非平凡的函数依赖 如果X——>Y,&a…...

devc++跑酷小游戏3.5.0
本来想搞存档的,失败了,要再学学文件操作的函数。还有一个打印地图的函数,更失败,彻底放弃。最近开学了,游戏不会经常更新,要写作业。昨天写到10点T_T #include<bits/stdc.h> #include<windows.h…...

Redisson限流算法
引入依赖 <dependency><groupId>org.redisson</groupId><artifactId>redisson-spring-boot-starter</artifactId><version>3.12.3</version> </dependency>建议版本使用3.15.5以上 使用 这边写了一个demo示例,定…...

GPT与MBR:硬盘分区表格式的革新与区别
概述 在计算机存储领域,硬盘分区是管理数据和操作系统部署的基础。两种广泛使用的分区表格式——MBR(Master Boot Record)和GPT(GUID Partition Table),各自代表了不同的技术阶段和发展需求。本文将详细介…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...
