【力扣hot100】刷题笔记Day15
前言
- 今天要刷的是图论,还没学过,先看看《代码随想录》这部分的基础
深搜DFS理论基础
-
深搜三部曲
- 确认递归函数、参数
- 确认终止条件
- 处理目前搜索节点出发的路径
-
代码框架
-
void dfs(参数) {if (终止条件) {存放结果;return;}for (选择:本节点所连接的其他节点) {处理节点;dfs(图,选择的节点); // 递归回溯,撤销处理结果} }
-
797. 所有可能的路径 - 力扣(LeetCode)
-
DFS
-
class Solution:def allPathsSourceTarget(self, graph: List[List[int]]) -> List[List[int]]:res = [] # 存放结果path = [0] # 当前路径def dfs(root: int):if root == len(graph) - 1: # 如果到达最后节点存入结果,res.append(path[:]) # path[:]避免使用引用,deep copyreturnfor node in graph[root]: # 遍历root所有节点path.append(node) # path加上当前遍历节点dfs(node) # 下一层继续搜索path.pop() # 回溯,撤销节点dfs(0)return res
-
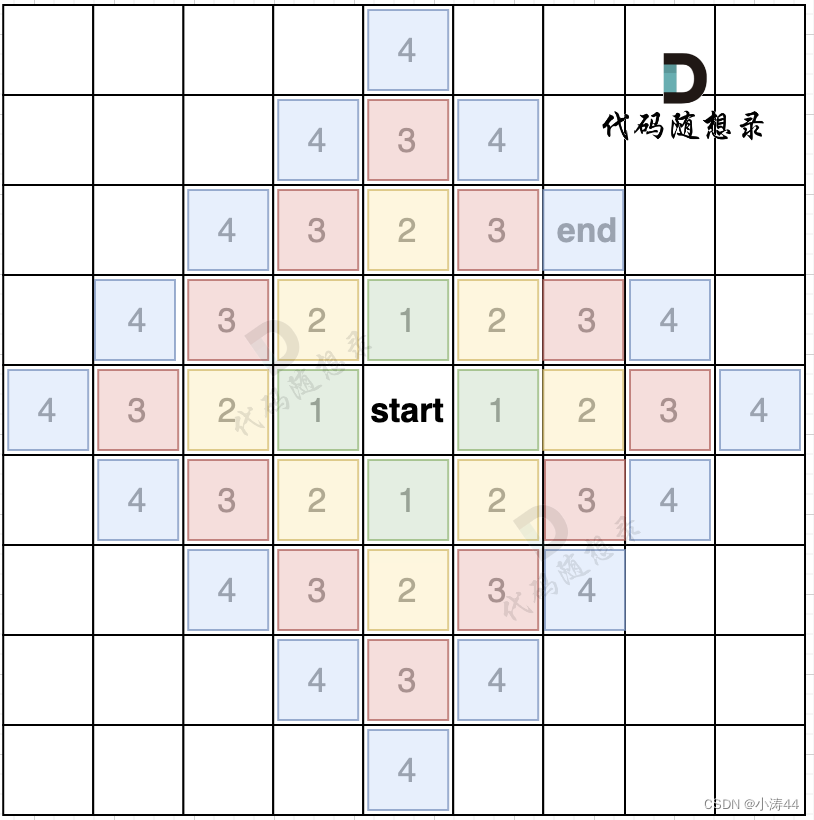
广搜BFS理论基础
- 适用于解决两个点之间的最短路径问题
-
from collections import deque dir = [(0, 1), (1, 0), (-1, 0), (0, -1)] # 创建方向元素def bfs(grid, visited, x, y):queue = deque() # 初始化队列queue.append((x, y)) # 放入第一个元素/起点visited[x][y] = True # 标记为访问过的节点while queue: # 遍历队列里的元素curx, cury = queue.popleft() # 取出第一个元素for dx, dy in dir: # 遍历四个方向nextx, nexty = curx + dx, cury + dyif nextx < 0 or nextx >= len(grid) or nexty < 0 or nexty >= len(grid[0]): continue # 越界了,直接跳过if not visited[nextx][nexty]: # 如果节点没被访问过 queue.append((nextx, nexty)) # 加入队列visited[nextx][nexty] = True # 标记为访问过的节点
200. 岛屿数量 - 力扣(LeetCode)
-
DFS
-
class Solution:def numIslands(self, grid: List[List[str]]) -> int:m, n = len(grid), len(grid[0])# visited = [[False] * n for _ in range(m)] # 如果不能修改用标记grid# 深搜当前陆地部分def dfs(x, y): # x表示行,y表示列grid[x][y] = "0" # 遍历到的节点就置为0以防重复,用visited则删除此句for nx, ny in [(x-1,y), (x+1,y), (x,y-1), (x,y+1)]:if 0 <= nx < m and 0 <= ny < n and grid[nx][ny] == "1":# if 0 <= nx < m and 0 <= ny < n and grid[nx][ny] == "1" and not visited[nx][ny]:# visited[nx][ny] = Truedfs(nx,ny)# 依次遍历每个节点搜索大陆res = 0for i in range(m):for j in range(n):if grid[i][j] == "1":# if not visited[i][j] and grid[i][j] == '1':# visited[i][j] = Trueres += 1 # 遇到没访问过的陆地,+1dfs(i, j)# 返回总陆地数return res
-
-
BFS
-
class Solution:def numIslands(self, grid: List[List[str]]) -> int:m, n = len(grid), len(grid[0])# visited = [[False] * n for _ in range(m)] # 如果不能修改用visited标记grid中已访问节点# 广搜当前陆地部分def bfs(x, y): # x表示行,y表示列q = deque()q.append((x,y))grid[x][y] = "0" # 遍历到的节点就置为0以防重复,用visited则删除此句# visited[x][y] = True # 用visitedwhile q:x0, y0 = q.popleft() # 当前遍历节点加入队列for nx, ny in [(x0-1,y0), (x0+1,y0), (x0,y0-1), (x0,y0+1)]:if 0 <= nx < m and 0 <= ny < n and grid[nx][ny] == "1": # 用visited则删除此句# if 0 <= nx < m and 0 <= ny < n and grid[nx][ny] == "1" and not visited[nx][ny]:q.append((nx, ny))grid[nx][ny] = "0" # 加入列表就标记为访问过,用visited则删除此句# visited[nx][ny] = True # 用visited # 依次遍历每个节点搜索大陆res = 0for i in range(m):for j in range(n):if grid[i][j] == "1":# if not visited[i][j] and grid[i][j] == '1':res += 1 # 遇到没访问过的陆地,+1bfs(i, j)# 返回总陆地数return res
-
-
并查集
- 没接触过并查集,依据这道题在B站大学找了相关视频和文章学习一下
-
## 解法三:UnionFind 并查集经典解法 class UnionFind: ## 定义为一个类。后面类似的题目,也可以直接搬去使用def __init__(self, grid): ## 初始化m, n = len(grid), len(grid[0])self.count = 0 ## count 是最终结果,初始化为0self.parent = [-1] * (m * n) ## 初始化 parent 数组取值全部为 -1## rank 秩,表示树的高度,在连接的时候要规定秩小的指向秩大的元素self.rank = [0] * (m * n) ## rank 用来实现上下左右的合并;初始化全部为 0 ## 计算陆地的总数 count;修改 parent 数组陆地元素的取值for i in range(m):for j in range(n):if grid[i][j] == "1": ## 对于陆地元素,把它的parent初始化为它的一维化的位置self.parent[i * n + j] = i * n + j ## parent初始化为元素本身的一维化的(位置)索引self.count += 1 ## 陆地总数## find 方法给union 方法调用def find(self, i):if self.parent[i] != i: ## 对于索引不等于自身的元素self.parent[i] = self.find(self.parent[i]) ## 路径优化。把所有链式关系,简化为一层的父子关系return self.parent[i] ## 返回父亲的索引(也等于该索引对应的取值)## 最关键是 union 方法,用来处理目标元素并计算岛屿数量def union(self, x, y):rootx = self.find(x) ## 找到自己的 root 索引rooty = self.find(y) ## 找到自己的 root 索引if rootx != rooty: ## 如果不等,则进行合并if self.rank[rootx] <= self.rank[rooty]: ## 如果 rank 更小self.parent[rootx] = rooty ## 秩小的指向秩大的元素else:self.parent[rooty] = rootx ## 秩小的指向秩大的元素if self.rank[rootx] == self.rank[rooty]: ## 如果秩相等self.rank[rootx] += 1 ## 如果深度相同,新节点的 rank + 1self.count -= 1 ## 合并一次,则陆地数量减一(岛屿数量=陆地数量-总的合并次数)## 主类 + 主函数 class Solution:def numIslands(self, grid: List[List[str]]) -> int: ## 主函数nr = len(grid) ## number of rowif nr == 0:return 0nc = len(grid[0]) ## number of columnuf = UnionFind(grid) ## 调用并查集函数## 遍历每一个位置for r in range(nr):for c in range(nc):if grid[r][c] == "1": ## 碰到陆地 1grid[r][c] = "0" ## 先修改为 0for x, y in [(r - 1, c), (r + 1, c), (r, c - 1), (r, c + 1)]: ## 遍历上下左右if 0 <= x < nr and 0 <= y < nc and grid[x][y] == "1": ## 碰到新的 1uf.union(r * nc + c, x * nc + y) ## 调用并查集函数return uf.count
后言
- 并查集这个学得我好累,这就是缺乏基础吧,路漫漫啊
相关文章:

【力扣hot100】刷题笔记Day15
前言 今天要刷的是图论,还没学过,先看看《代码随想录》这部分的基础 深搜DFS理论基础 深搜三部曲 确认递归函数、参数确认终止条件处理目前搜索节点出发的路径 代码框架 void dfs(参数) {if (终止条件) {存放结果;return;}for (选择:本节点…...

vue-显示数据
v-text和v-html专门用来展示数据, 其作用和插值表达式类似。v-text和v-html可以避免插值闪烁问题. 当网速比较慢时, 使用{{}}来展示数据, 有可能会产生插值闪烁问题。 插值闪烁: 在数据未加载完成时,页面会显示出原始的{{}}, 过一会才会展示正常数据.语法…...

kali linux常用命令
1. 网络扫描 功能:网络扫描是用来发现网络中的设备、服务和开放端口的过程。 命令:nmap 例子:nmap -sP 192.168.1.0/24 这个命令使用 Nmap 进行网络扫描,列出 192.168.1.0/24 网段中的所有活跃主机。 2. 密码破解 功能…...
HTML5:七天学会基础动画网页4
backgorund-size 值与说明 length(单位像素):设置背景图片高度和宽度,第一个值设置宽度,第二个值设置高度,如果只给出一个值,第二个是设置为auto。 percentage(百分比):以父元素的百分比来设置背景图像的宽度和高度,…...

Web安全之接口鉴权
目录 接口鉴权定义 为什么会有cookie还有session还有token这种技术的存在?...

shardingsphere 集成springboot【水平分表】
创建sharding_sphere数据库 在数据库中创建两张表,t_order_1和t_order_2 分片规则:如果订单编号是偶数添加到t_order_1,如果是奇数添加到t_order_2 创建实体类 public class Order { private Integer id; private Integer orderType; private Int…...
GO 的 Web 开发系列(六)—— 遍历路径下的文件
文件 IO 处理是程序的基础功能,WEB 程序中通过文件 IO 实现附件的上传与下载。在 GO 中,有多种方式可以遍历文件目录,获取文件路径,本文从使用层面上论述这些函数。 预先准备一个包含子目录的目录,用于遍历测试&#…...

Flutter 处理异步操作并根据异步操作状态动态构建界面的方法FutureBuilder
概述 当界面的内容需要依靠网络请求的数据,就需要处理苦恼的,状态是空,非空的逻辑了,不然页面构建可能会报错,而FutureBuilder提供了一个非常好的解决方法,直接看代码 代码 异步操作函数 即网络请求函数…...
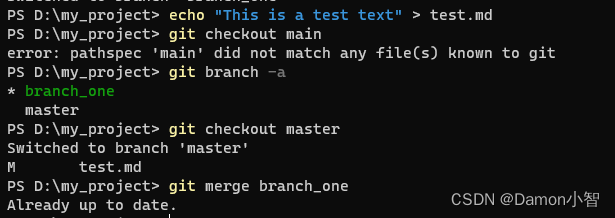
Git教程-Git的基本使用
Git是一个强大的分布式版本控制系统,它不仅用于跟踪代码的变化,还能够协调多个开发者之间的工作。在软件开发过程中,Git被广泛应用于协作开发、版本管理和代码追踪等方面。以下是一个详细的Git教程,我们将深入探讨Git的基本概念和…...

Java解决长度为K子的数组中的的最大和
Java解决长度为K子的数组中的的最大和 01 题目 给你一个整数数组 nums 和一个整数 k 。请你从 nums 中满足下述条件的全部子数组中找出最大子数组和: 子数组的长度是 k,且子数组中的所有元素 各不相同 。 返回满足题面要求的最大子数组和。如果不存在子…...
【手机端测试】adb基础命令
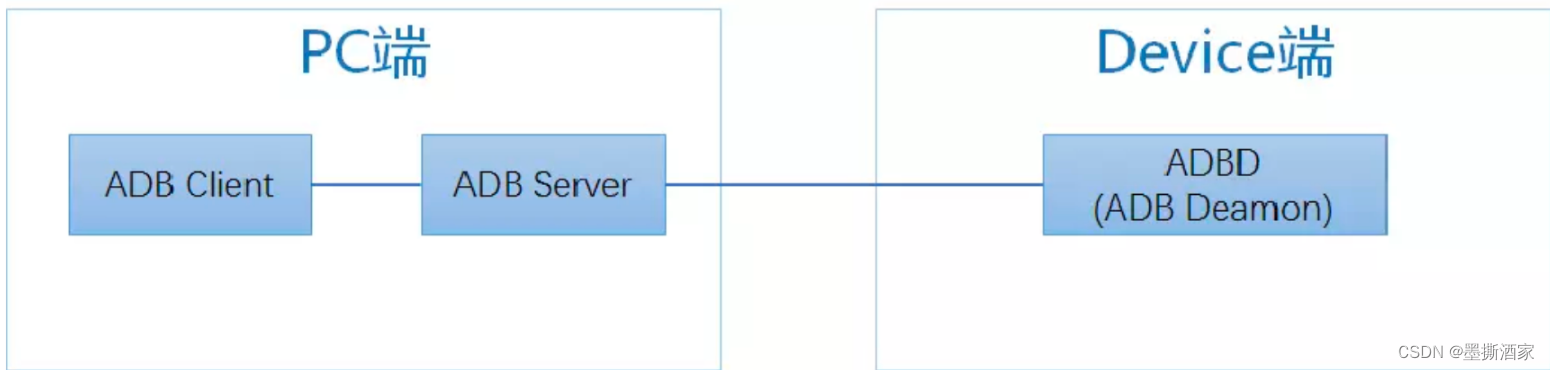
一、什么是adb adb(Android Debug Bridge)是android sdk的一个工具 adb是用来连接安卓手机和PC端的桥梁,要有adb作为二者之间的维系,才能让用户在电脑上对手机进行全面的操作。 Android的初衷是用adb这样的一个工具来协助开发人…...

【数据结构】深入探讨二叉树的遍历和分治思想(一)
🚩纸上得来终觉浅, 绝知此事要躬行。 🌟主页:June-Frost 🚀专栏:数据结构 🔥该文章主要讲述二叉树的递归结构及分治算法的思想。 目录: 🌍前言:🌍…...
 和 post() 方法—— W3school 详解 简单易懂(二十四))
jQuery AJAX get() 和 post() 方法—— W3school 详解 简单易懂(二十四)
jQuery get() 和 post() 方法用于通过 HTTP GET 或 POST 请求从服务器请求数据。 HTTP 请求:GET vs. POST 两种在客户端和服务器端进行请求-响应的常用方法是:GET 和 POST。 GET - 从指定的资源请求数据POST - 向指定的资源提交要处理的数据 GET 基本…...

Linux中如何进行LVM逻辑卷扩容?
#注意:如果lv所在的vg有空间直接扩容就ok了! 1.创建pv pvcreate /dev/sdb 执行以上命令得到以下内容: Physical volume "/dev/sdb" successfully created. 2.直接vgextend扩容 vgextend vg1 /dev/sdb #卷组名字,将…...

现代企业架构框架——应用架构
现代企业架构框架——应用架构。 现代企业架构中的应用架构是指企业在构建和维护应用系统时所采用的一种架构框架。应用架构旨在实现应用系统的可扩展性、灵活性、可维护性和可重用性,以满足企业在数字化时代对应用系统的快速交付和持续创新的需求。下面将详细介绍应用架构的…...

期货开户保证金保障市场正常运转
期货保证金是什么?在期货市场上,采取保证金交易制度,投资者只需按期货合约的价值,交一定比率少量资金即可参与期货合约买卖交易,这种资金就是期货保证金。期货保证金(以下简称保证金〕按性质与作用的不同。…...

WebGIS----wenpack
学习资料:https://webpack.js.org/concepts/ 简介: Webpack 是一个现代化的 JavaScript 应用程序的模块打包工具。它能够将多个 JavaScript 文件和它们的依赖打包成一个单独的文件,以供在网页中使用。 Webpack 还具有编译和转换其他类型文…...

【Maven】Maven 基础教程(二):Maven 的使用
《Maven 基础教程》系列,包含以下 2 篇文章: Maven 基础教程(一):基础介绍、开发环境配置Maven 基础教程(二):Maven 的使用 😊 如果您觉得这篇文章有用 ✔️ 的话&#…...
mirthConnect忽略HTTPS SSL验证
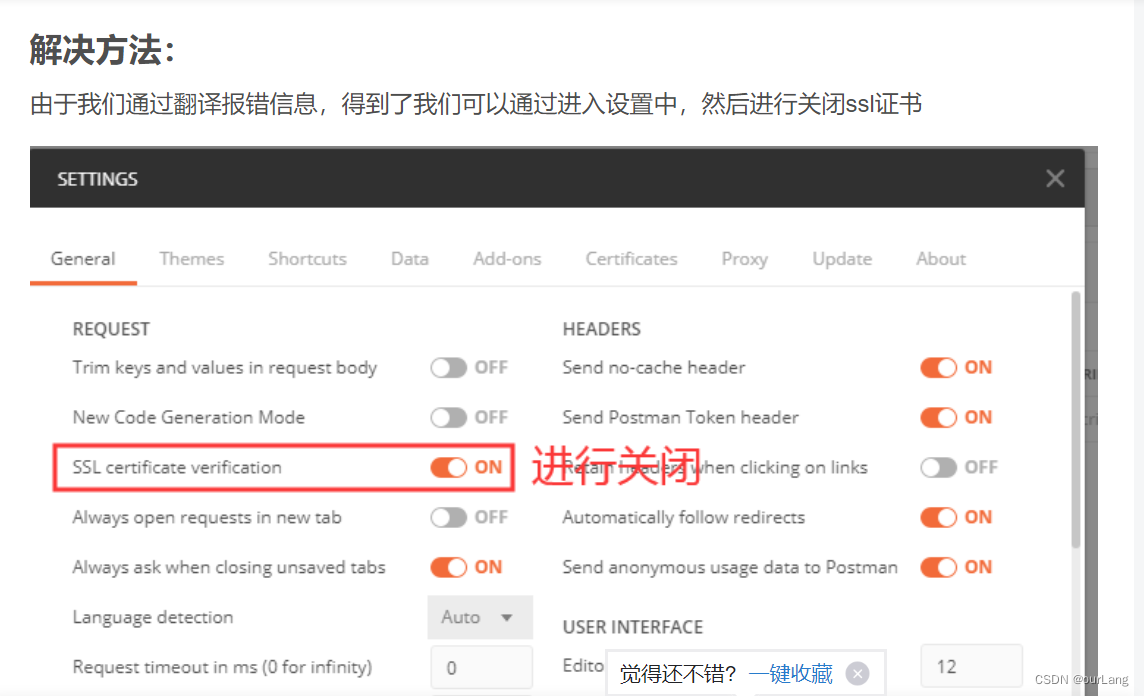
mirthConnect SSL忽略验证 1、下载https网站证书 点击不安全---->证书无效 2、查看mirth 秘钥库口令 在mirthConnect 的conf目录下面keystore.storepass 3、导入证书到本地 在jdk的bin目录下面执行 keytool -importcert -file "下载的网站证书路径" -keysto…...
libvirt命名空间xmlns:qemu的使用
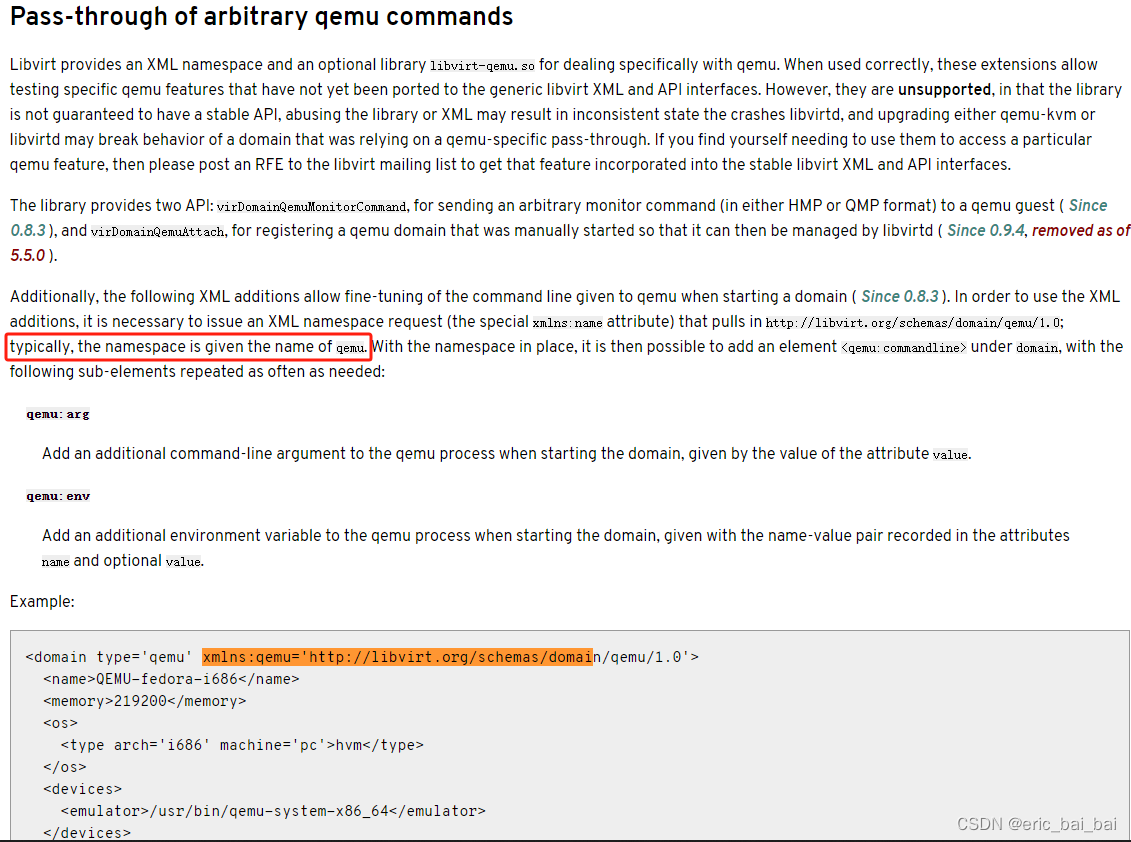
示例xml <domain type{domain_type} xmlns:qemuhttp://libvirt.org/schemas/domain/qemu/1.0><qemu:commandline><qemu:commandline><qemu:arg value-newarg/><qemu:env nameQEMU_ENV valueVAL/></qemu:commandline></domain>"…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...
