机试指南:Ch5:线性数据结构 Ch6:递归与分治
文章目录
- 第5章 线性数据结构
- 1.向量 vector
- 2.队列 queue
- (1)队列的特点、应用
- (2)基本操作
- (3)例题
- 例题1:约瑟夫问题2 (难度:中等)
- (4)习题
- 习题1:排队打饭 (难度:中等)
- 3.栈 stack
- (1)栈的特点、应用
- (2)基本操作
- (3)例题
- 例题1:编排字符串 (难度:简单)
- 例题2:括号匹配 (难度:中等)
- 例题3:计算表达式 (难度:困难)
- (4)习题
- 习题1:堆栈的使用 (难度:简单)
- 习题2:模拟出入栈游戏 (难度:中等)
- 习题3:简单计算器 (难度:困难)
- 第6章 递归与分治
- 1.递归
- (1)原理
- ①函数
- ②递归
- (2)例题
- 例题1:n的阶乘 (难度:入门)
- 例题2:汉诺塔Ⅲ (难度:简单)【分治法-递归】
- 2.分治
- (1)原理
- (2)例题
- 例题1:跳台阶 (难度:简单)
- 例题2:不连续1的子串(难度:中等)
- 例题3:2的幂次方(难度:困难)
- (3)习题
- 习题1:Fibonacci (难度:入门)
- 习题2:二叉树 (难度:简单)【递归】
- 习题3:骨牌铺地砖 (难度:简单) 【动态规划】
- 习题4:矩阵幂 (难度:中等) 【矩阵计算】
- 习题5:全排列 (难度:困难)【递归回溯法 - DFS】
第5章 线性数据结构
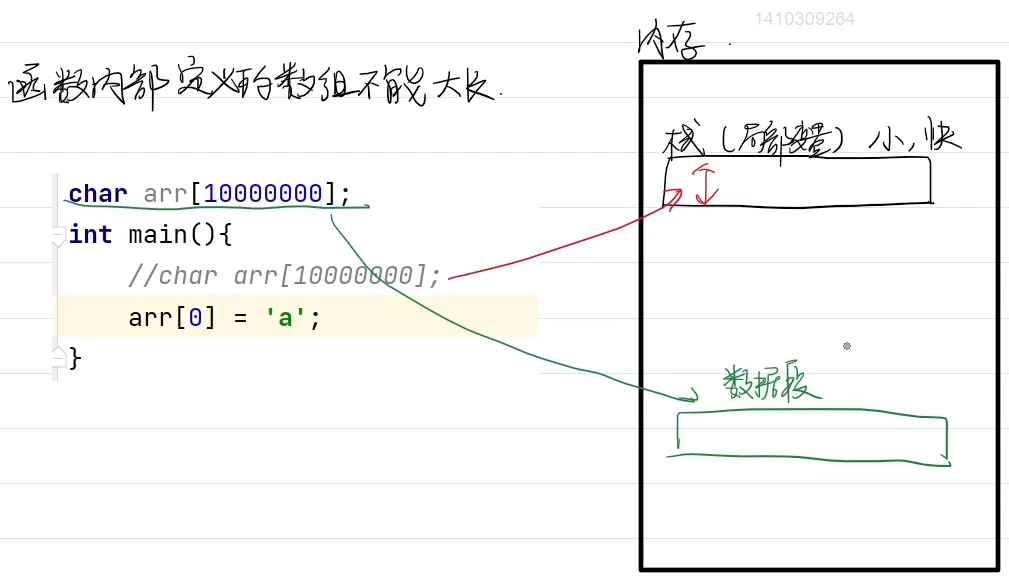
1.当定义的数组特别大,达到1千万时,不能定义在函数内部,会崩溃。栈比较小,但快。
要定义在全局位置,数据段中。
【局部大数组会崩溃,全局大数组不会崩溃】
2.标准模板库STL
1.向量 vector
vector是动态数组,长度可改变。 vector<int> vec;//创建空向量,长度为0
普通静态数组长度是固定不变的。int arr[100];//创建长度为100的静态数组
1.头文件
#include <vector>
using namespace std;
2.声明向量
vector<int> vec;//长度为0
3.赋初值
vector<int> vec2 = {1,2,3};
4.申请一定空间的向量,所有元素初值默认为0
vector<int> vec3(10000);
※5.尾部插入:尾部扩容 push_back(元素) 。效率最高,插入n个为O(n),插入1个为O(1)。
vec.push_back(1);//vec[0]=1
vec.push_back(3);//vec[1]=3
※6.任意位置插入:
vec.insert(pos,[个数,]内容);//头部插入字符串
vec.insert(vec.begin(),str);
※7.尾部删除:弹出尾部元素 pop_back()
vec.pop_back();
※8.下标访问
vec[i] //下标>=n时,数组越界
9.长度计算
vec.size();
10.两种遍历方法
①下标遍历
for(unsigned int i = 0; i < vec.size(); ++i){printf("vec[%d] = %d\n",i,vec[i]);
}
②迭代器遍历
for(vector<int>::iterator it = vec.begin(); it != vec.end(); ++it){printf("vec[] = %d\n",*it);
}
11.随机位置的插入:insert(位置,元素)
vector<int>::iterator it1 = vec.begin()+1;//迭代器指针指向vector的第二个位置
vec.insert(it1,3);//在vector第二个位置插入元素3
12.随机位置的删除:erase(位置);
vec.erase(vec.begin());//删除vector的第一个位置的元素
13.vector的实现原理
(1)vector的组成、申请空间(堆上)
vector是类类型,包括size容量、capacity内存大小、ptr首地址
首地址存放在栈上,但vector申请的内存空间在堆区上,堆区比栈区大,因此vector可申请空间比静态数组在栈上申请的空间可以大很多。【静态数组 - 栈 - 小空间。 vector - 堆- 大空间】
(2)vector的扩容机制
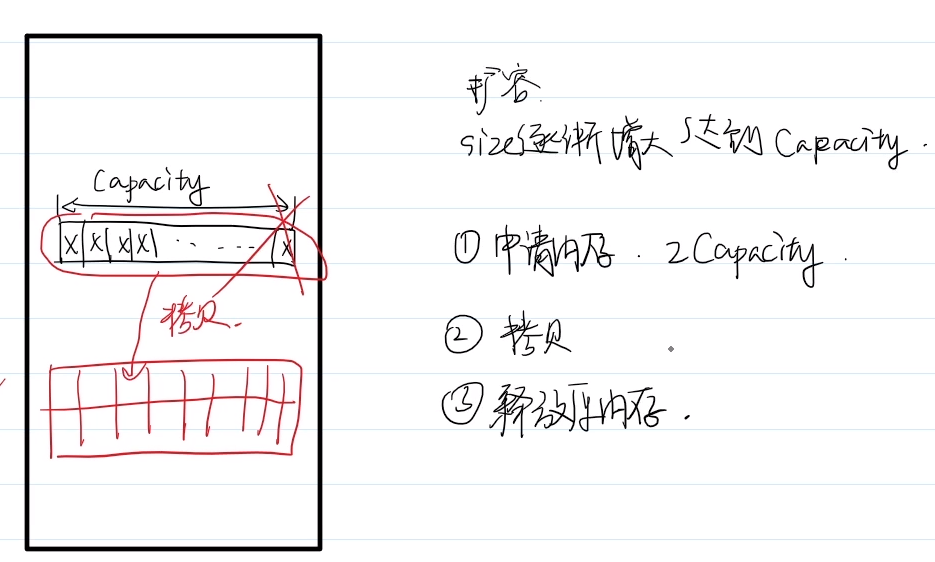
2.队列 queue
(1)队列的特点、应用
1.队列的特点
队列queue是受限制的线性表
先进先出,FIFO
队尾入队,队头出队。
2.队列应用:
广度优先遍历 BFS
(2)基本操作
0.头文件
#include <queue>
using namespace std;queue<int> myQueue;
1.队尾入队 .push(变量名)
for(int i = 0;i <= 5;++i){myQueue.push(i);
}
2.队头出队 .pop()
3.判空 .empty()
4.队首元素 .front()
5.队尾元素 .back()
#include <iostream>
#include <queue>
using namespace std;int main() {//队列初始化queue<int> myQueue;//判空if(myQueue.empty()){cout << "myQueue is empty!" << endl;}//队尾入队for(int i = 0 ; i < 10; ++i){myQueue.push(i);//打印队首、队尾cout << "队首:" << myQueue.front() << " 队尾:" << myQueue.back() << endl;}cout << "---------------" << endl;//队首出队for(int i = 0 ; i < 9; ++i){myQueue.pop();//打印队首、队尾cout << "队首:" << myQueue.front() << " 队尾:" << myQueue.back() << endl;}return 0;
}
(3)例题
例题1:约瑟夫问题2 (难度:中等)
提交网址:http://bailian.openjudge.cn/practice/3254


思路:队头元素插入队尾,然后队头元素出队,以此实现循环队列
#include <iostream>
#include <queue>
using namespace std;int main() {queue<int> myQueue;int n,p,m;while(cin >> n >> p >> m){if(n==0 && p==0 && m==0) break;//初始化队列for(int i = 1; i <= n; ++i){myQueue.push(i);}//将编号为p旋转到队头for(int i = 1; i < p; ++i) { //将1到p-1号元素从队头调整到队尾myQueue.push(myQueue.front()); //队头元素插入队尾myQueue.pop(); //队头出队}//开始计数过程while(!myQueue.empty()){//将m-1个元素从队头调整到队尾for(int i = 1; i < m; ++i){myQueue.push(myQueue.front());myQueue.pop();}//打印并移除第m个元素cout << myQueue.front();if(myQueue.size() > 1) cout << ",";myQueue.pop();}cout << endl;}return 0;
}
(4)习题
习题1:排队打饭 (难度:中等)
提交网址:https://www.acwing.com/problem/content/description/5063/

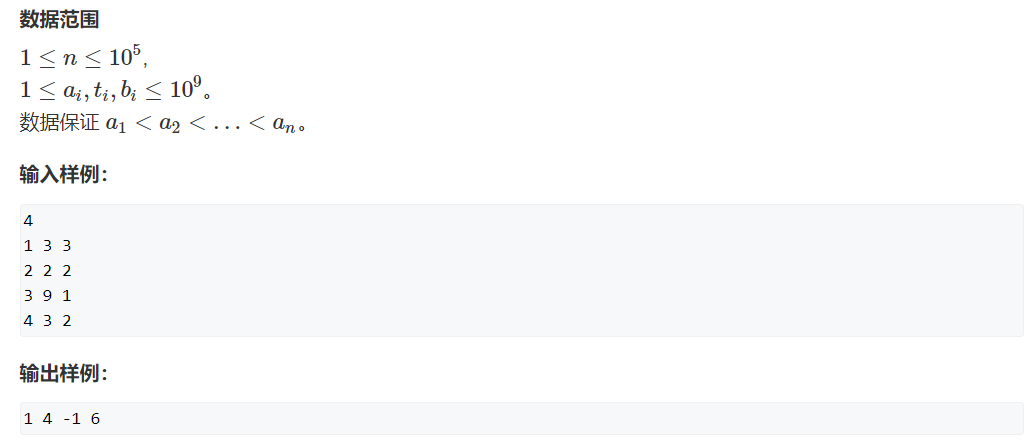
几个注意事项:
①可能前面有连续几个没打上饭的,得用int记录而不是bool
②有些数值超过了int的表示范围,将数组由int类型改为long long
#include <iostream>
using namespace std;int main() {int n;long long a[100010],t[100010],b[100010],res[100010]; //a[i]为到达时刻,t[i]为打饭耗时,b[i]为最大等待时长,res[i]为打饭时刻或-1cin >> n;for(int i = 1; i <= n; ++i){cin >> a[i] >> t[i] >> b[i];}res[1] = a[1]; //第一位同学到达后立即开始打饭cout << res[1] <<" ";int count = 0; //count记录前面有连续多少位同学没有打上饭for(int i = 2; i <= n; ++i){if(a[i]+b[i] < res[i-1-count]+t[i-1-count]){ //上一位开始打饭时间+打饭耗时超过了该同学最大等待时间,则放弃打饭cout << "-1 ";count++;}else{res[i] = max(res[i-1-count]+t[i-1-count],a[i]); //max(最早可以打饭时刻,该同学到达时间)cout << res[i] << " ";count = 0;}}cout << endl;return 0;
}
3.栈 stack
(1)栈的特点、应用
1.栈的特点
栈也是操作受限的线性表,只能一端进出。
后进先出
栈,禁止操作的一端称为盲端。允许元素插入和删除的一端称为栈顶。
2.栈的应用
①深度优先遍历 DFS:逆序输出
②表达式解析、表达式求值
③递归
④括号匹配
(2)基本操作
0.头文件
#include <stack>
using namespace std;
1.初始化
stack<typename> myStack//定义
2.方法
.push():压栈,将元素加入栈中
.pop():弹栈
.top():获取栈顶内容
.size():栈大小
.empty():判断栈是否为空
#include <iostream>
#include <stack>
using namespace std;int main() {//栈初始化stack<int> myStack;//栈判空if(myStack.empty()){cout << "myStack is empty!" << endl;}//入栈(压栈)for(int i = 0; i < 10 ; ++i){myStack.push(i);cout << "top is " << myStack.top() << endl;}cout << "---------------" <<endl;//出栈(弹栈)for(int i = 0 ; i < 9; ++i){myStack.pop();cout << "top is " << myStack.top() << endl;}return 0;
}
(3)例题
例题1:编排字符串 (难度:简单)
提交网址:https://www.acwing.com/problem/content/3578/


思路:准备一个临时栈,用于演示弹栈
#include <iostream>
#include <stack>
#include <string>
using namespace std;int main() {string str;stack<string> myStack,tempStack;int m;cin >> m;for(int i = 0; i < m; ++i){cin >> str;myStack.push(str);tempStack = myStack;for(int i = 1; !tempStack.empty(); ++i){if(i > 4) break; //最多输出4个字符串cout << i << "=" << tempStack.top() << " ";tempStack.pop();}cout << endl;}return 0;
}
例题2:括号匹配 (难度:中等)
提交网址:https://www.acwing.com/problem/content/3696/
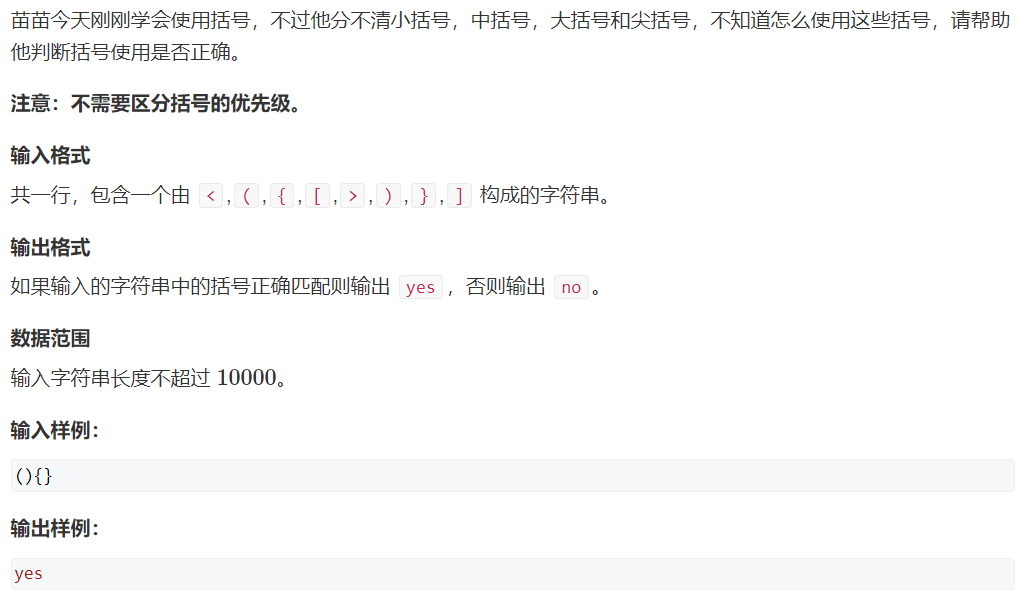
思路:栈实现。遇到右括号都是同一种思路,写好一个else if,后面都是复制了
#include <iostream>
#include <string>
#include <stack>
using namespace std;int main() {stack<char> myStack;string str;cin >> str;for(int i = 0; i < str.size(); ++i){//1.遇到左括号,入栈if(str[i] == '<' || str[i] == '(' || str[i] == '[' || str[i] == '{'){myStack.push(str[i]);}//2.遇到右尖括号else if(str[i] == '>'){if(myStack.empty() || myStack.top()!='<'){cout << "no" << endl;return 0;}else{ //栈顶就是左尖括号,匹配myStack.pop();}}//3.遇到右小括号else if(str[i] == ')'){if(myStack.empty() || myStack.top()!='('){cout << "no" << endl;return 0;}else{ //栈顶就是左小括号,匹配myStack.pop();}}//4.遇到右中括号else if(str[i] == ']'){if(myStack.empty() || myStack.top()!='['){cout << "no" << endl;return 0;}else{ //栈顶就是左中括号,匹配myStack.pop();}}//5.遇到右大括号else if(str[i] == '}'){if(myStack.empty() || myStack.top()!='{'){cout << "no" << endl;return 0;}else{ //栈顶就是左大括号,匹配myStack.pop();}}}if(myStack.empty()) cout << "yes" << endl;else cout << "no" << endl;return 0;
}
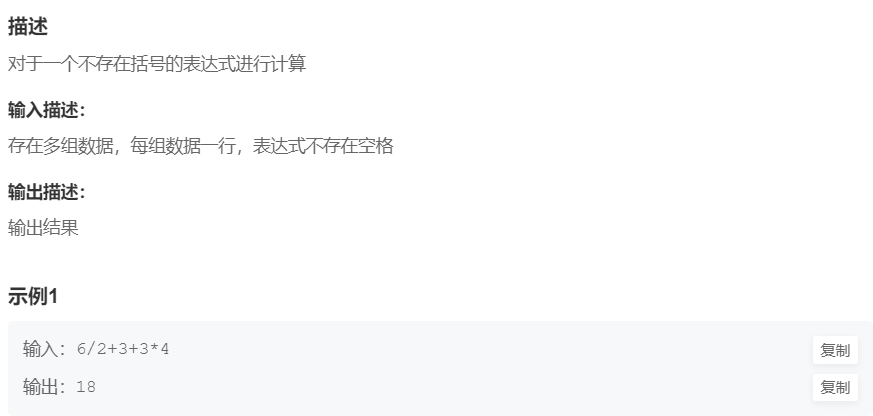
例题3:计算表达式 (难度:困难)
提交网址:http://t.cn/AiKKJjJ5
#include <stdio.h>
#include <string>
#include <stack>
#include <map>
using namespace std;
int main() {char str[1000] = { 0 };map<char, int> priority = {{'\0',0},{'+',1},{'-',1},{'*',2},{'/',2}};while (scanf("%s", str) != EOF) {string numStr = "";stack<char> opStack;stack<double> numStack;for (int i = 0; ; ++i) {if (str[i] >= '0' && str[i] <= '9') {numStr.push_back(str[i]);}else {double num = stod(numStr);numStr = "";numStack.push(num);// 什么时候弹栈? 栈非空 && 新op的优先级 不高于 栈顶的优先级// 循环弹栈和计算while (!opStack.empty() &&priority[str[i]] <= priority[opStack.top()]) {double rhs = numStack.top();numStack.pop();double lhs = numStack.top();numStack.pop();char curOp = opStack.top();opStack.pop();if (curOp == '+') {numStack.push(lhs + rhs);}else if (curOp == '-') {numStack.push(lhs - rhs);}else if (curOp == '*') {numStack.push(lhs * rhs);}else if (curOp == '/') {numStack.push(lhs / rhs);}}// 栈为空 或者 新op的优先级高于栈顶if (str[i] == '\0') {printf("%d\n", (int)numStack.top());break;}else {opStack.push(str[i]);}}}}return 0;
}
(4)习题
习题1:堆栈的使用 (难度:简单)
提交网址:http://t.cn/AiKKM6F6


#include <iostream>
#include <stack>
using namespace std;int main() {int n;while(cin >> n){stack<int> myStack;char c;int a;for(int i = 0; i < n; ++i){cin >> c;if(c == 'A'){if(myStack.empty()) cout << "E" << endl;else cout << myStack.top() << endl;}else if(c == 'P'){cin >> a;myStack.push(a);}else if(c == 'O'){if(!myStack.empty()) myStack.pop();}}}return 0;
}
习题2:模拟出入栈游戏 (难度:中等)
提交网址:https://www.acwing.com/problem/content/3681/
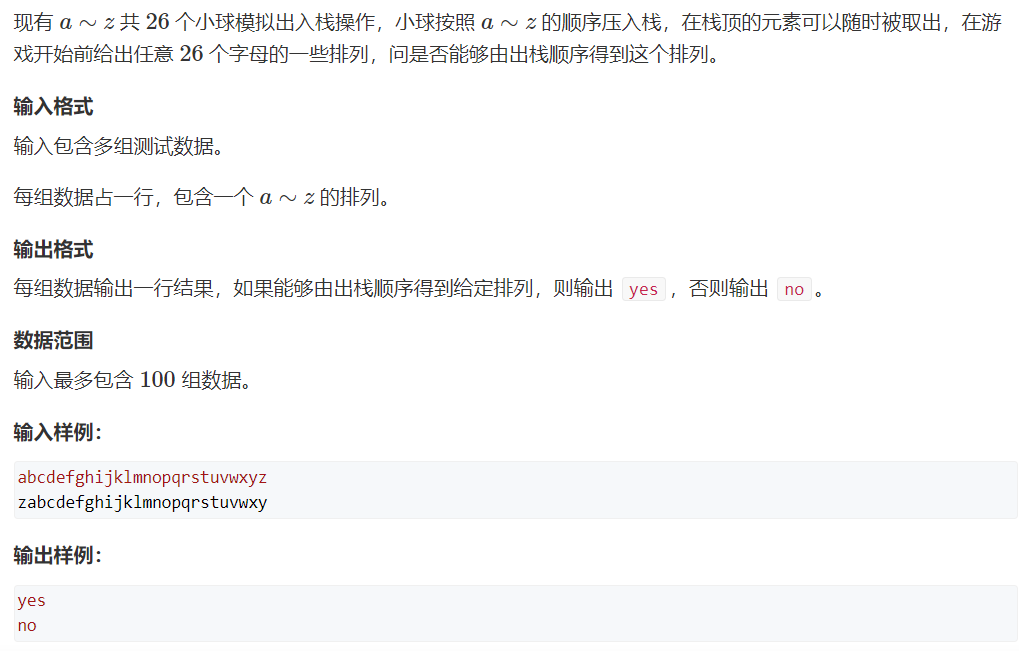
注意,栈的初始化放在while循环里。放在外面可能会因为上一轮未清空,受脏数据影响
#include <iostream>
#include <stack>
#include <string>
using namespace std;int main() {string str1 = "abcdefghijklmnopqrstuvwxyz",str2;while(cin >> str2){stack<char> stk;int k = 0;for(int i = 0 ; i < str1.size(); ++i){stk.push(str1[i]);while(stk.size() && k < str2.size() && stk.top() == str2[k]){//核心while循环:stk.pop(); //比较栈顶元素和字符串str2中当前位置的字符是否相等k++;}}if(stk.empty()) cout << "yes" << endl;else cout << "no" << endl;}return 0;
}
习题3:简单计算器 (难度:困难)
提交网址:http://t.cn/AiKoGS94

第6章 递归与分治
1.递归
(1)原理
1.什么是递归?
函数在函数体内调用自身函数的行为叫做递归
(在函数定义中调用本函数,叫做递归)
2.递归的原理:
①代码段:PC走到被调函数的入口
②栈区:栈帧压入栈内
逐过程、逐语句
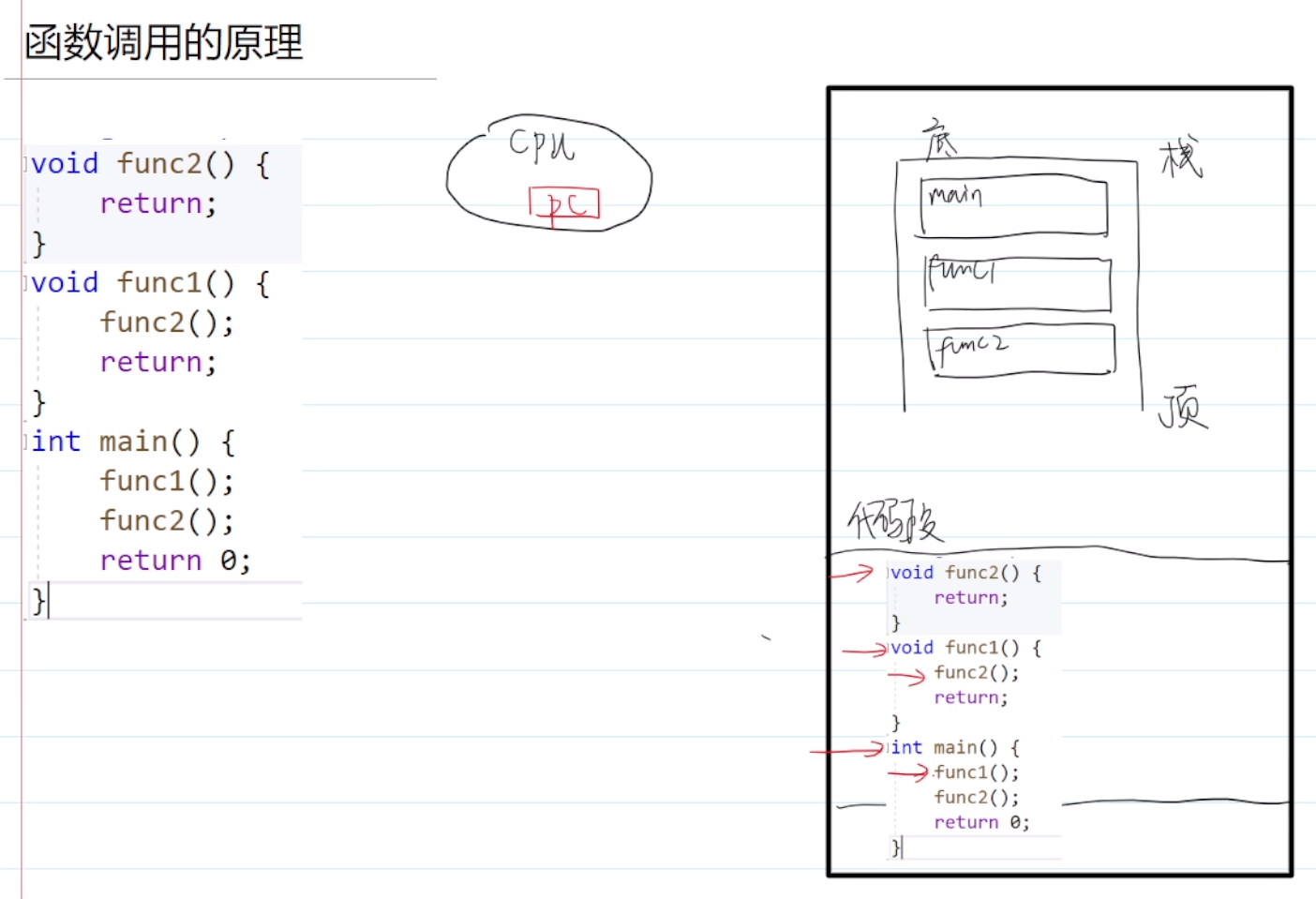
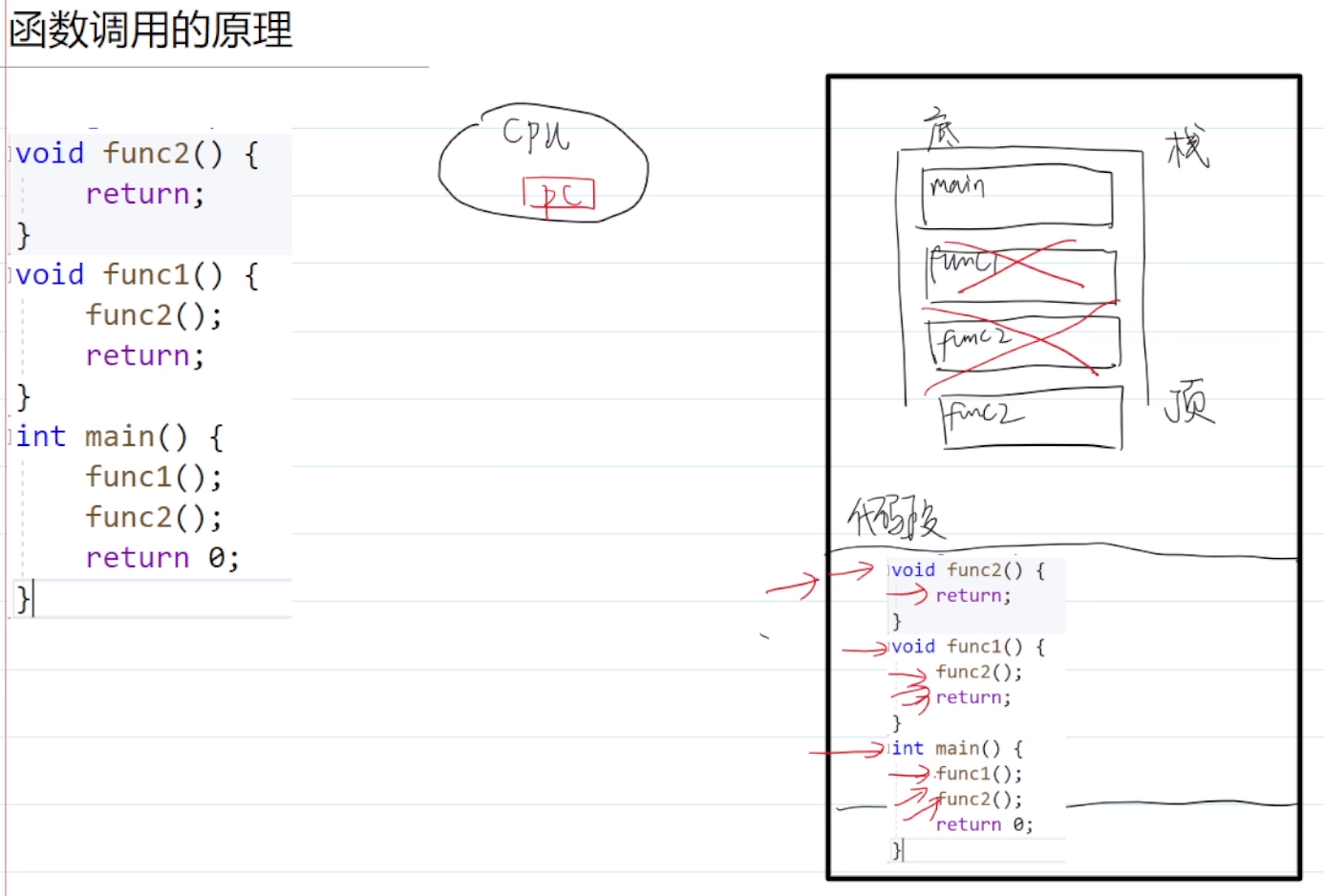
3.如何使用递归?
①递归一定要有递归出口
②每次递归,变量条件向着递归出口靠近
4.递归与分治的关系:
分治是一种思想,分而治之;递归是一种实现方法,函数调用自己。
分治思想可用递归来实现,也可以用其他方法来实现。递归作为一种方法,不止可以用于实现递归思想,也可以用来实现其他思想。
但总的来说,一般都用递归方法来实现分治的思想。故两者本不是同一纬度的概念,但是经常放在一起谈论。
常见的分治:求斐波那契数列、快速排序
常见的递归:求n的阶乘
5.2023旧版本内容:
从函数到递归
①大问题→小问题,等价条件
②确定最小问题,即递归出口
①函数
C语言编写的代码,以函数定义为单位。
call:把PC移到被调函数
ret:把PC移回主调函数
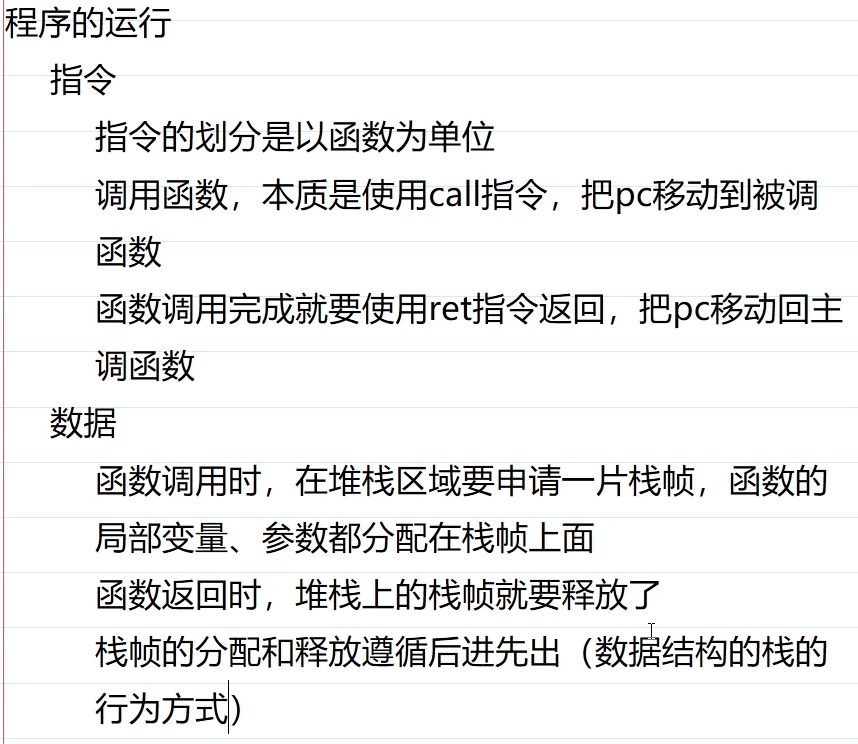
②递归
递归关注的两个点:
①大问题转化为小问题:规模n→规模n-1
②最小问题:递归出口
(2)例题
例题1:n的阶乘 (难度:入门)
提交网址:https://www.nowcoder.com/share/jump/2891302591709206218373

C++:
#include <iostream>
using namespace std;long long factorial(int n){if(n == 0 || n == 1) return n;else{return n * factorial(n-1);}
}int main(){int n;cin >> n;cout << factorial(n);return 0;
}
C语言:
#include <cstdio>long long int Factorial(int n){if(n == 0){return 1;}else{return n*Factorial(n-1);}
}int main(){int n;while(scanf("%d",&n) != EOF){printf("%lld",Factorial(n));}return 0;
}
例题2:汉诺塔Ⅲ (难度:简单)【分治法-递归】


思路:
①n-1片为整体,先由第一柱搬到第三柱,最大片由第一柱搬到第二柱;[Hanoi(n-1) + 1]
②n-1片从第三柱搬回第一柱,最大片由第二柱搬到第三柱; [Hanoi(n-1) + 1]
③n-1片由第一柱搬到第三柱,完成。[Hanoi(n-1)]
#include <iostream>
using namespace std;long long Hanoi(int n){ //搬运n片共需要Hanoi(n)步if(n == 1){return 2; }else{return 3 * Hanoi(n-1) + 2; }
}int main() {int n;while(cin >> n){cout << Hanoi(n) << endl;}return 0;
}
2.分治
(1)原理
1.名称解释
分治法,分而治之 (divide-and-conquer method)
2.分治法的两个要素
①大问题转化为相似的小问题,直至转化为最小问题
②最小问题的解决方案

3.分治法的代码模板
①分解:大问题拆成小问题
②治理:找到等价条件,解决递归出口(最小问题)
③合并

(2)例题
例题1:跳台阶 (难度:简单)
提交网址:https://www.acwing.com/problem/content/823/
思路:因为每次只能走1级或2级台阶,所以走n级台阶只会是从n-1或n-2级台阶上去的。根据加法原理,这两种方案的数量可以相加得到走n级台阶的方案。同样的,走n-1级的方案可以拆分为走n-2级和走n-3级方案之和。

#include <iostream>
using namespace std;int f(int n){if(n == 1){return 1;}else if(n == 2){return 2;}else{return f(n-1) + f(n-2);}
}int main() {int n; //n级台阶while(cin >> n){cout << f(n) << endl;}return 0;
}
测试可得:
f(1)=1,f(2)=2,f(3)=3,f(4)=5,f(5)=8,f(6)=13,f(7)=21 …
可知,跳台阶问题是斐波那契数列问题的变形,即后一个值是前两个值之和。
优化分析:
但是由栈帧示意图,我们发现很多f(n)会重复计算多次。当n很大时,该算法的效率会很低。我们自然而然地想到如何避免重复计算从而提高函数的效率。
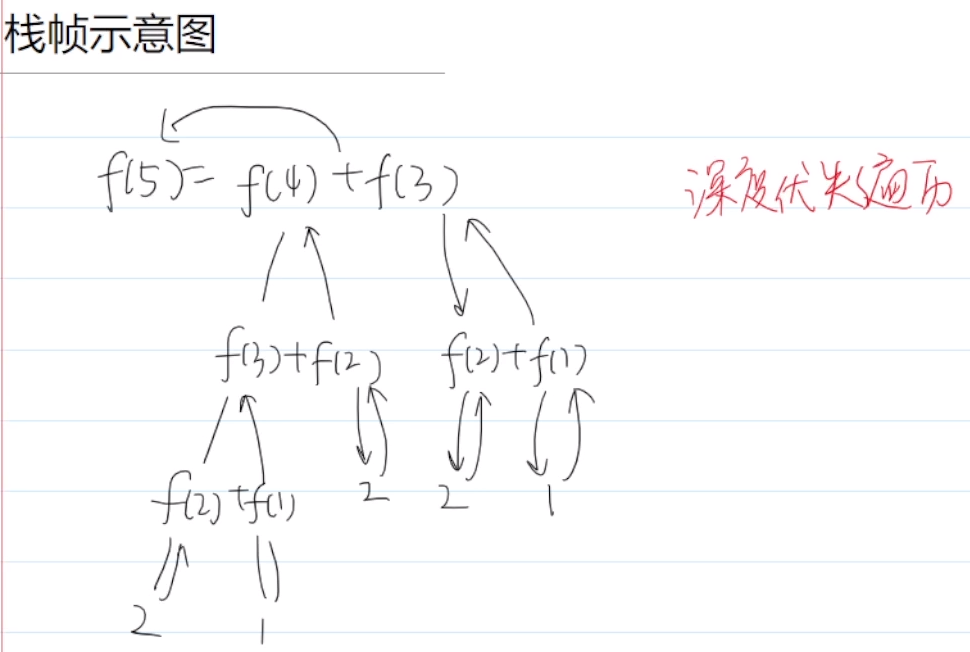
优化:用数组存储已经计算过的结果
例题2:不连续1的子串(难度:中等)
提交网址:https://www.acwing.com/problem/content/3709/
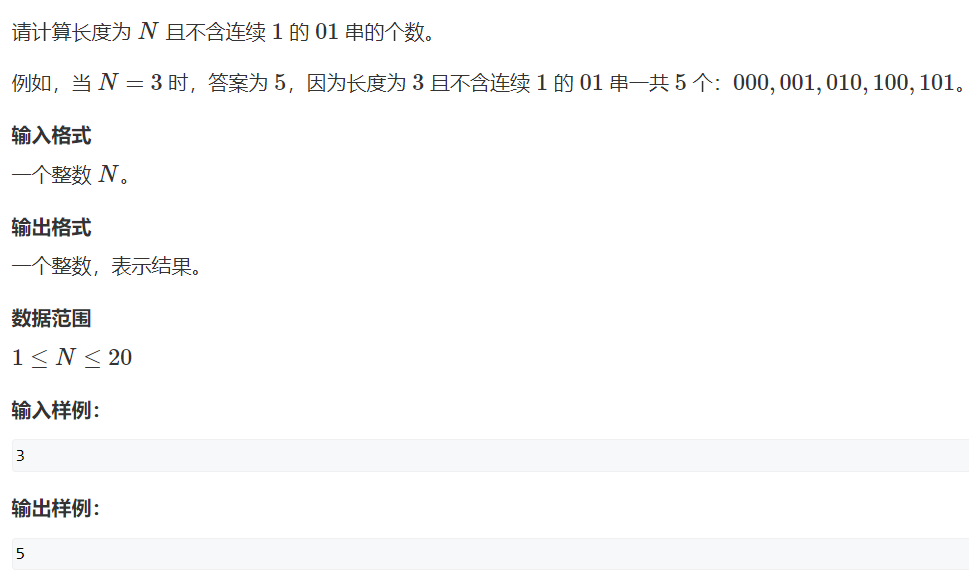
24炉灰老师:分解为小问题,并给出最小问题的解决方案(递归出口)
#include <iostream>
using namespace std;int f0(int n); // 函数声明写在前面,
int f1(int n); // 则这两个函数就可以交叉调用int f0(int n){ // 末尾为0if(n == 1){return 1;}else{return f0(n-1) + f1(n-1);};
}int f1(int n){ // 末尾为1if(n == 1){return 1;}else{return f0(n-1);}
}int main() {int n;while(cin >> n){cout << f0(n)+f1(n) << endl;}return 0;
}
例题3:2的幂次方(难度:困难)
提交网址:https://www.acwing.com/problem/content/3486/

分析:由大问题分解为小问题,用分治法

将n转化为2的指数形式:

24炉灰老师
#include <stdio.h>
#include <string>
#include <vector>
using namespace std;
string Get2sExponet(int n) {if (n == 0) {return "0";}vector<int> exp;for (int i = 15; i >= 0; --i) {if ((n & (1 << i)) != 0) {exp.push_back(i);}}// n = 2^(exp[0]) + 2^(exp[1]) + ... + 2^(exp[size-1])string res = "";for (int i = 0; i < exp.size(); ++i) {if (i != 0) {res += "+";}if (exp[i] == 1) {res += "2";}else {res += "2(" + Get2sExponet(exp[i]) + ")";}}return res;
}
int main() {int n;while (scanf("%d", &n) != EOF) {printf("%s\n", Get2sExponet(n).c_str());}return 0;
}
(3)习题
习题1:Fibonacci (难度:入门)
提交网址:http://t.cn/Ai0K3tU5
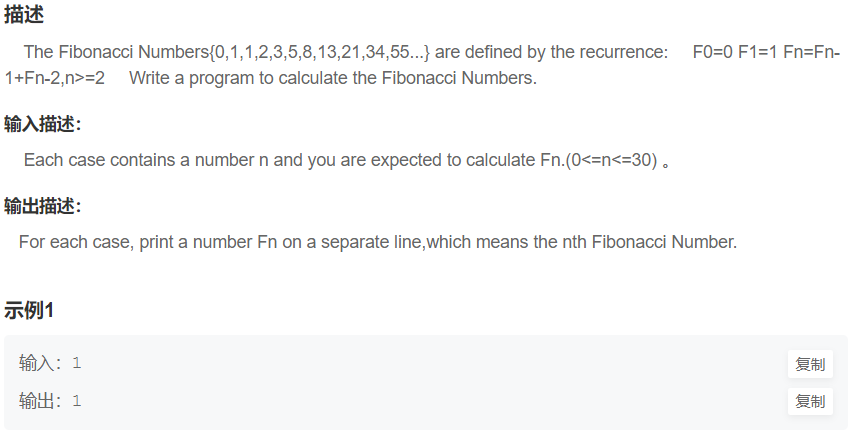
解法1:斐波那契数列,递归实现
C语言版本:
#include <cstdio>int Fibonacci(int n ){if(n == 0 || n == 1){return n;}else{return Fibonacci(n-1) + Fibonacci(n-2);}
}int main(){int n;while(scanf("%d",&n) != EOF){printf("%d\n",Fibonacci(n));}return 0;
}
C++版本:
#include <iostream>
using namespace std;int Fibonacci(int n){if(n == 0 || n == 1){return n;}else{return Fibonacci(n-1) + Fibonacci(n-2);}
}int main(){int n;while(cin >> n){cout << Fibonacci(n);}return 0;
}
解法2:斐波那契数列(非递归实现,循环实现)
#include <cstdio>int fib(int n){int n1 = 1;int n2 = 1;int ret = 0;if (n==1 || n==2){return 1;}for (int i = 3; i <= n; i++){ //通过循环计算n>=3时ret = n1 + n2;n1 = n2;n2 = ret;}return ret;
}int main(){int n = 0;scanf("%d", &n);int ret = fib(n);printf("%d\n",ret);return 0;
}
解法3:斐波那契数列(非递归实现,动态规划实现)
#include <cstdio>int dp[91];int Fibonacci(int n){dp[1] = 1;dp[2] = 2;for(int i = 3 ; i <= n; ++i){ //3-ndp[i] = dp[i-1] + dp[i-2];}return dp[n];
}int main(){int n;while(scanf("%d",&n) != EOF){printf("%d\n",Fibonacci(n));}return 0;
}
习题2:二叉树 (难度:简单)【递归】
提交网址:http://t.cn/Ai0Ke6I0
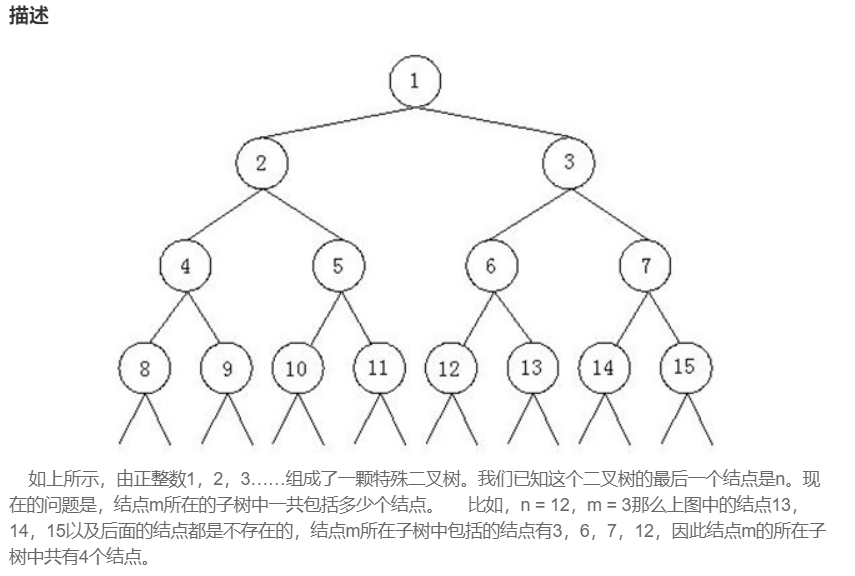

C++版本:根结点 + 左子树 + 右子树
如图,编号为m的结点,左孩子编号为2m,右孩子编号为2m+1
#include <iostream>
using namespace std;int binarytree(int m,int n){if(m > n){return 0;}else{ //如图,编号为m的结点,左孩子编号为2m,右孩子编号为2m+1return 1 + binarytree(2*m,n) + binarytree(2*m+1,n); //根结点 + 左子树 + 右子树}
}int main(){int m,n; //m为父结点编号,n为总结点数while(cin >> m >> n){if(m==0 && n==0) break;cout << binarytree(m,n) << endl;}return 0;
}
C语言版本:
#include <cstdio>int binaryTree(int m,int n){if(m>n){return 0;}else{return binaryTree(2*m,n) + binaryTree(2*m+1,n) + 1;}
}int main(){int m,n;while(scanf("%d %d",&m,&n) != EOF){if(m<=0 && n<=0){break;}printf("%d\n",binaryTree(m,n));}
}
习题3:骨牌铺地砖 (难度:简单) 【动态规划】
提交网址:https://www.acwing.com/problem/content/3690/
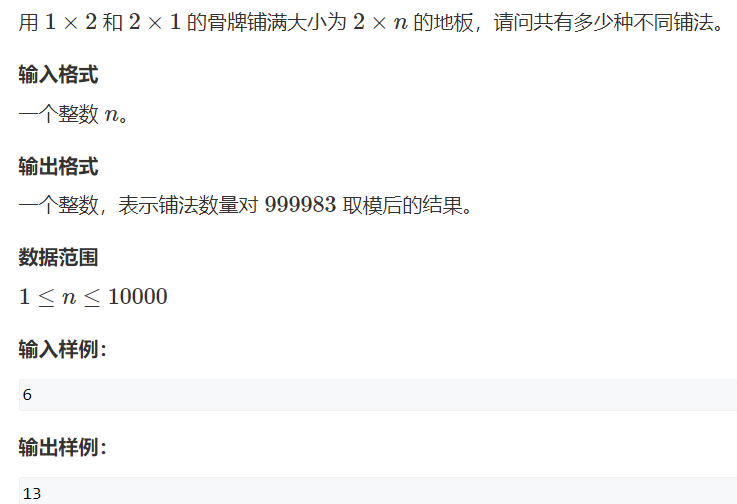
思路:
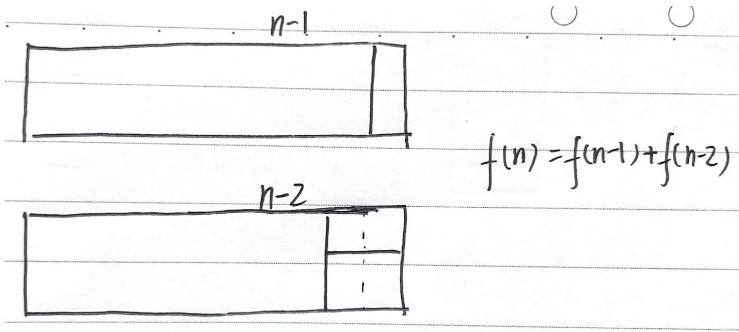
用递归会超时,改用动态规划,数组保存计算结果,避免重复计算
#include <iostream>
using namespace std;int dp[10010];long long Fibonacci(int n){dp[0] = 0;dp[1] = 1;dp[2] = 2;for(int i = 3; i <= n; ++i){dp[i] = (dp[i-1] + dp[i-2]) % 999983;}return dp[n];
}int main() {int n;cin >> n;cout << Fibonacci(n);return 0;
}
习题4:矩阵幂 (难度:中等) 【矩阵计算】
提交网址:https://www.acwing.com/problem/content/3690/
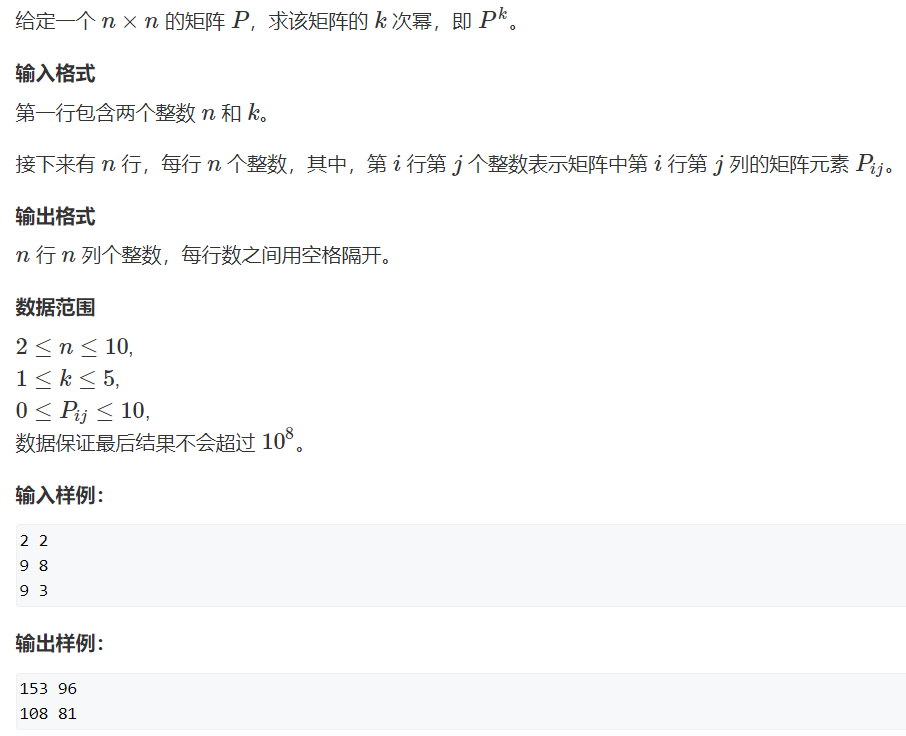
学会计算 矩阵C = A×B
核心代码:
for(int i = 0; i < n; ++i){for(int j = 0; j < n; ++j){for(int k = 0; k < n; ++k){ //矩阵C = 矩阵A × 矩阵B:C[i][j] += A[i][k]*B[k][j]; //C[i][j] = A的第i行×B的第j列所有对应元素}}
}
答案:
#include <iostream>
#include <cstring>
using namespace std;
const int N = 11;
int A[N][N],B[N][N],C[N][N];int main() {int n,m; //n为矩阵的阶,m为矩阵的幂cin >> n >> m;memset(A,0,sizeof(A));//输入矩阵Afor(int i = 0; i < n; ++i){for(int j = 0; j < n; ++j){cin >> A[i][j];}}//计算m次幂//(1)若m为1,输出原矩阵if(m == 1){for(int i = 0; i < n; ++i){for(int j = 0; j < n; ++j){cout << A[i][j] << " ";}cout << endl;}return 0;}//(2)若m>1,计算 矩阵 C = A×Bmemcpy(B,A,sizeof(A));while(--m){memset(C,0,sizeof(C));for(int i = 0; i < n; ++i){for(int j = 0; j < n; ++j){for(int k = 0; k < n; ++k){ //矩阵C = 矩阵A × 矩阵B:C[i][j] += A[i][k]*B[k][j]; //C[i][j] = A的第i行×B的第j列所有对应元素}}}memcpy(B,C,sizeof(C)); //这次的幂次运算结果C赋值给B}//输出矩阵Cfor(int i = 0; i < n; ++i){for(int j = 0; j < n; ++j){cout << C[i][j] << " ";}cout << endl;}return 0;
}
习题5:全排列 (难度:困难)【递归回溯法 - DFS】
提交网址:https://www.acwing.com/problem/content/3690/

来自一位网友的答案:
#include<bits/stdc++.h>
using namespace std;
void backtracking(string tmp,string s)
{if(tmp.size()==s.size())cout<<tmp<<endl;else{for(int i=0;i<s.size();++i){if(tmp.find(s[i])!=tmp.npos) continue;backtracking(tmp+s[i],s);}}
}
int main()
{string s,tmp=""; while(cin>>s)backtracking(tmp,s); return 0;}
相关文章:

机试指南:Ch5:线性数据结构 Ch6:递归与分治
文章目录 第5章 线性数据结构1.向量 vector2.队列 queue(1)队列的特点、应用(2)基本操作(3)例题例题1:约瑟夫问题2 (难度:中等) (4)习题习题1:排队打饭 (难度:中等) 3.栈 stack(1)栈…...

展厅设计的理念是什么
1、立足当地文化 升华本地精神 ,因地制宜,深入挖掘本土文化特色,撷取其精华,灵活运用、巧妙融入,做到掌控宏观全局。 重点突出,努力打造本土拳头品牌,挖掘其内涵,拓展延伸、着重展示…...

springboot 定时任务备份mysql数据库
记录在Linux 系统上定时备份MySQL数据库 1、在代码中添加备份 package org.jeecg.modules.xczxhhr.job;import lombok.extern.slf4j.Slf4j; import org.quartz.Job; import org.quartz.JobExecutionContext;import java.io.BufferedReader; import java.io.File; import java…...

PMP考试之20240301
1、在回顾项目团队最新的绩效报告时,项目经理注意到他们的产出出现了重大下降。项目经理决定: A.增加每个团队成员在截止日期前完成任务的压力 B.增加状态报告和团队评审会议的频率 C.为表现最好的团队成员提供特别奖励 D.改善和促进团队成员之间的信任和凝聚力…...
什么是MAC地址? win10电脑查看MAC地址的多种方法
您是否知道连接到家庭网络的每件硬件都有自己的身份?正如每个设备都分配有自己的 IP 地址一样,每个硬件都有一个唯一的网络标识符。 该标识符称为MAC 地址。MAC 代表媒体访问控制。您可能需要 MAC 地址来解决网络问题或配置新设备。在 Windows 中查找您…...
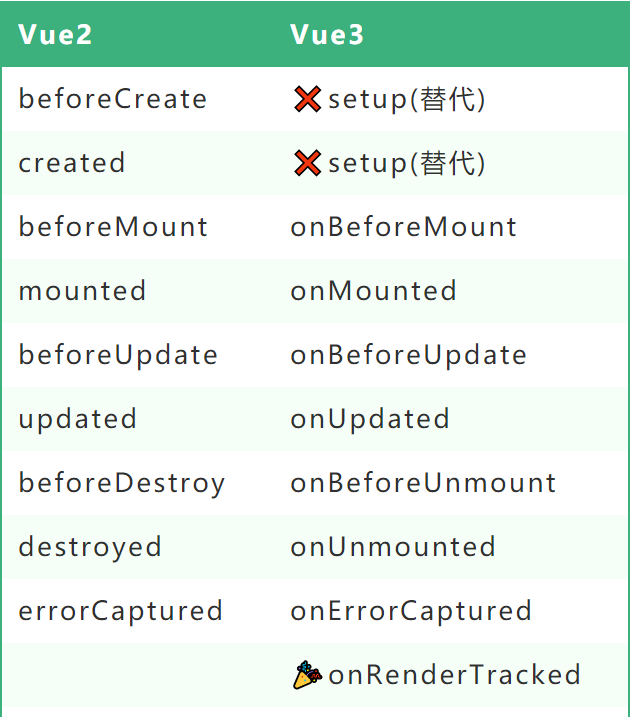
vue3中的基本语法
目录 基础素材 vue3的优化 使用CompositionAPI理由 1. reactive() 函数 2. ref() 函数 2.1. ref的使用 2.2. 在 reactive 对象中访问 ref 创建的响应式数据 3. isRef() 函数 4. toRefs() 函数 5. computed() 5.1. 通过 set()、get()方法创建一个可读可写的计算属性 …...

Timeplus-proton流处理器调研
概念 Timeplus是一个流处理器。它提供强大的端到端功能,利用开源流引擎Proton来帮助数据团队快速直观地处理流数据和历史数据,可供各种规模和行业的组织使用。它使数据工程师和平台工程师能够使用 SQL 释放流数据价值。 Timeplus 控制台可以轻松连接到不…...
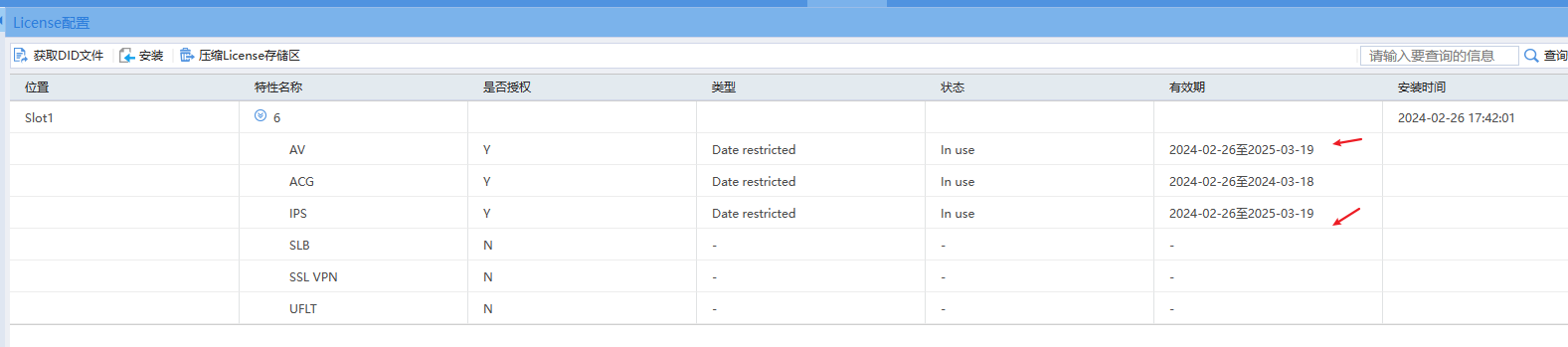
H3C防火墙安全授权导入
一、防火墙授权概述 前面我们已经了解了一些防火墙的基本概念,有讲过防火墙除了一些基本功能,还有一些高级安全防护,但是这些功能需要另外独立授权,不影响基本使用。这里以H3C防火墙为例进行大概了解下。 正常情况下,防…...

使用 OpenCV 通过 SIFT 算法进行对象跟踪
本文介绍如何使用 SIFT 算法跟踪对象 在当今世界,当涉及到对象检测和跟踪时,深度学习模型是最常用的,但有时传统的计算机视觉技术也可能有效。在本文中,我将尝试使用 SIFT 算法创建一个对象跟踪器。 为什么人们会选择使用传统的计…...

SHELL 脚本: 导出NEO4j DUMP并上传SFTP
前提 开通sftp账号 安装expect 示例 NEO4J_HOME/path/to/neo4j # neo4j 安装目录 DUMP_PATH/data/dump # DUMP本地保存目录 DUMP_FILEneo4j_$(date %F).dump #导出文件名称 UPLOAD_DIR/path/to/stfp/dump/ #上传目录 $NEO4J_HOME/bin/neo4j-admin dump --databaseneo4j --t…...

Vue 封装一个函数,小球原始高度不固定,弹起比例不固定、计算谈几次后,高度低于1米
## 简介 本文将介绍如何使用Vue封装一个函数,计算小球弹跳的次数,直到高度低于1米。函数的参数包括小球的原始高度和弹起比例。通过代码案例演示了如何使用Vue进行封装和调用。 ## 函数封装 vue <template> <div> <label for&qu…...

外地人能申请天津公租房吗?2024天津积分落户租房积分怎么加?
相关推荐:在天津工作的外地人可以申请天津公共租赁住房吗? 外地人可以申请天津公共租赁住房吗? 2024年定居天津租房如何加分? 根据《天津居住证积分指标及积分表》的规定,在天津租房也可以参加积分结算,每…...
)
毕业设计——基于springboot的聊天系统设计与实现(服务端 + 客户端 + web端)
整个工程包含三个部分: 1、聊天服务器 聊天服务器的职责一句话解释:负责接收所有用户发送的消息,并将消息转发给目标用户。 聊天服务器没有任何界面,但是却是IM中最重要的角色,为表达敬意,必须要给它放个…...

公告栏功能:自动弹出提醒,重要通知不再错过
发布查询时,您是否遇到这样的困扰: 1、查询发布时间未到,学生进入查询主页后发现未发布任何查询,不断进行咨询。 2、有些重要事项需要进入查询主页就进行强提醒,确保人人可见,用户需要反馈“我知道了”才能…...
网络编程学习
思维导图 代码练习 TCP实现通信 服务器端代码 #include <myhead.h> #define SER_IP "192.168.152.135" #define SER_PORT 8910 int main(int argc, const char *argv[]) {//1创建用于监听的套接字int sfd -1;sfd socket(AF_INET,SOCK_STREAM,0)…...
centos物理电脑安装过程(2024年1月)
开机时:CtrlAltDelete键重启电脑 重启开始时:按F11,桌面弹出蓝色框,选择第二个SSK SFD142 1.00,回车 选择install centos7安装 选择后弹出选择安装选项,选择语言 连接无线网络 安装设置,选择磁…...
Web自动化测试平台开发---Automated_platform
一、项目简介 历时一个假期,Automated_platform 第一版完工,是一款基于po模式的自动化测试平台,采用后端技术为DjangoceleryRabbitMQmysql 配置mysql数据库,进行数据迁移后,运行项目后,即可成功访问http://127.0.0.1:8…...

mybatis-plus: 多租户隔离机制
文章目录 一、TenantLineHandler1、介绍2、包含的方法 二、简单实例三、实践1、实现TenantLineHandler接口 一、TenantLineHandler 1、介绍 TenantLineHandler 是 Mybatis-Plus 中用于处理多租户的接口,用于实现多租户数据隔离的具体逻辑。通过实现这个接口&#…...

用Socks5代理游戏,绕过“网络海关”去探险
1. 出海大冒险的开始 在游戏世界,就像在现实生活中一样,有时我们需要越过海洋去探索未知的世界。但是,网络上也有一些“海关”,限制我们访问某些网站或游戏服务器。这就是我们今天要克服的挑战! 2. Socks5代理…...
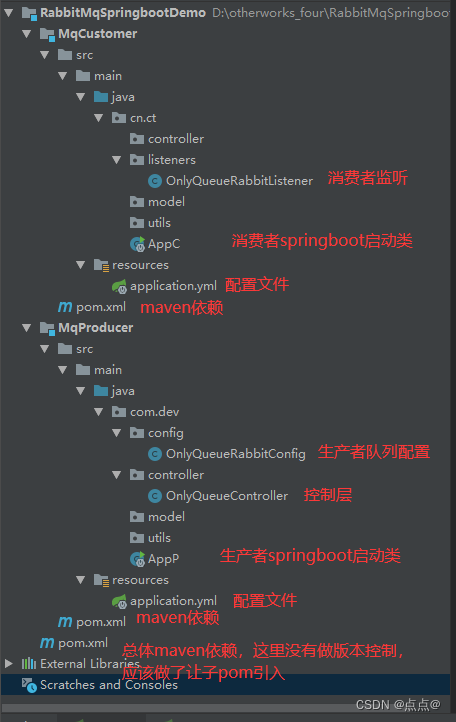
SpringBoot整合rabbitmq-直连队列,没有交换机(一)
说明:本文章只是springboot和rabbitmq的直连整合,只使用队列生产和消费消息,最简单整合! 工程图: A.总体pom.xml <?xml version"1.0" encoding"UTF-8"?><project xmlns"http://…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
