数据结构与算法 - 数组与二分查找 + Leetcode典型题
1. 什么是数组
数组是存放在连续内存空间上的相同类型数据的集合。
数组可以方便的通过下标索引的方式获取到下标下对应的数据。
C++中二维数组在地址空间上也是连续的。
需注意:
- 数组的下标从0开始。
- 数组内存空间的地址是连续的。
- 数组的元素是不能删的,只能覆盖。
2. 二分查找
力扣题目链接
之前的题解704. 二分查找中有一些地方不够清晰,此处补充说明。
数组为有序数组+数组中无重复元素 -> 考虑二分法
- 在计算
mid时,考虑数据溢出的可能,应将mid = (low + high) / 2;写为
int mid = left + ((right - left) / 2); //防止溢出
- 二分法根据选择的区间不同,有两种解决方式,分别为:左闭右闭 [left, right] 和左闭右开 [left, right)
-
在左闭右闭 [left, right] 的情况下,nums [right] 表示数组中最后一个元素,
while (left <= right)要使用 <= ,因为 left == right 是有意义的。且每次判断if (nums[mid] > target)后,由于nums[mid]一定不是target,right 要赋值为 middle - 1,right = mid - 1;,这表示下一次要查找的左区间结束下标位置为 middle - 1,即区间为 [left, middle - 1]。
同理,if (nums[mid] < target)时, left 要赋值为 middle + 1。 -
在左闭右开 [left, right) 的情况下,nums [right] 无意义,
while (left < right)中使用**<**,因为 left == right 在区间 [left, right) 是没有意义的。每次判断if (nums[mid] > target)后,nums[mid]不等于target,在左区间 [left, mid) 中继续寻找.
区间右开:right更新为mid。
区间左闭:if (nums[mid] < target)时,left 要更新为 mid + 1
- 二分查找时间复杂度为 O(log n)
相关题目1:35. 搜索插入位置
补充之前题解35. 搜索插入位置-二分查找中表达不清晰的地方。
这道题存在四种情况:
- 目标值在数组所有元素之前
- 目标值等于数组中某一个元素
- 目标值插入数组中的某一位置
- 目标值在数组所有元素之后
与上一道题的差别在于1,3,4情况下的返回值。在左闭右闭 [left, right] 的情况下,right = mid - 1;,(1情况下此时 right = -1;3情况下 right 指向应插入的前一个位置;4情况下 right 指向最后一个元素的位置)所以应返回 right + 1 ,即return right + 1;;在左闭右开 [left, right) 的情况下,right = mid;,所以应返回 right ,即return right;。
相关题目2:69.x的平方根 367.有效的完全平方数
题解:【LeetCode-简单】69.x的平方根 + 367.有效的完全平方数 - 二分法
相关题目3:【LeetCode-中等】34. 在排序数组中查找元素的第一个和最后一个位置 - 二分法
3. 移除元素 - 双指针
力扣题目链接
题解:【LeetCode-简单】27.移除元素 - 数组与双指针法
由于Leetcode中数组是用的vector,这道题可以用nums.erase(it);函数暴力破解,但要注意erase()函数在删除元素后会将位于该元素后方的剩余元素前移,这将导致数组长度的改变以及后续元素下标的变化,删除元素后迭代器 it 不需要 it++便已经指向了下一个元素。
不考虑vector的因素,由于数组的元素在内存地址中是连续的,不能单独删除数组中的某个元素,只能覆盖。本题可采用双指针的方法。
双指针法(快慢指针法): 通过一个快指针和慢指针在一个for循环下完成两个for循环的工作。
下面定义本题中的快慢指针:
- 快指针:寻找新数组(不含有目标元素的数组)的元素 ,即用于寻找不等于
val的元素 - 慢指针:指向更新新数组下标的位置,即指向需要被覆盖的等于
val的元素
最终慢指针一定指向了最终数组末尾的下一个元素,只要返回慢指针即可。
题目中提及元素的顺序可以改变,同向双指针和相向双指针都可以使用,如果要求不能改变元素顺序,则应该使用同向双指针。
4. 有序数组的平方 - 双指针
力扣题目链接
典型的双指针问题,暴力解法的时间复杂度是O(nlogn),而采用双指针的时间复杂度是O(n)。
题解:【LeetCode-简单】977. 有序数组的平方-双指针
5. 长度最小的子数组 - 滑动窗口
力扣题目链接
题解:【LeetCode-中等】209.长度最小的子数组-双指针/滑动窗口
所谓滑动窗口,就是不断的调节子序列的起始位置和终止位置,从而得出我们要想的结果。
在暴力解法中,是一个for循环滑动窗口的起始位置,一个for循环为滑动窗口的终止位置,用两个for循环完成了一个不断搜索区间的过程。滑动窗口只用一个for循环来完成这个操作。
而这个循环的索引,一定是表示 滑动窗口的终止位置。
直观的动画演示:
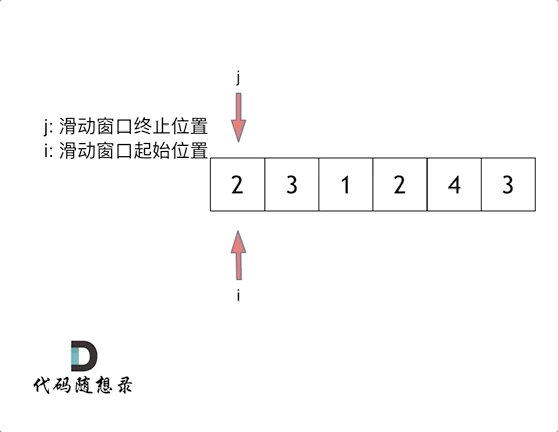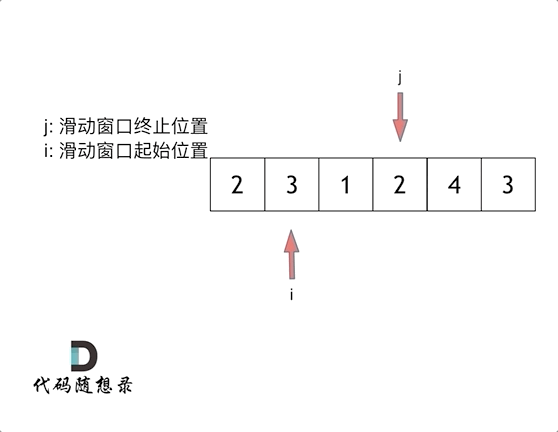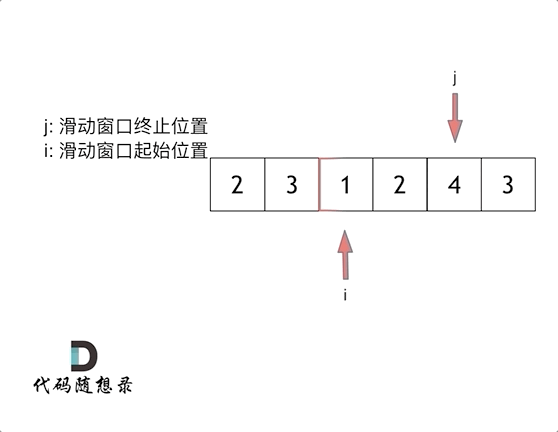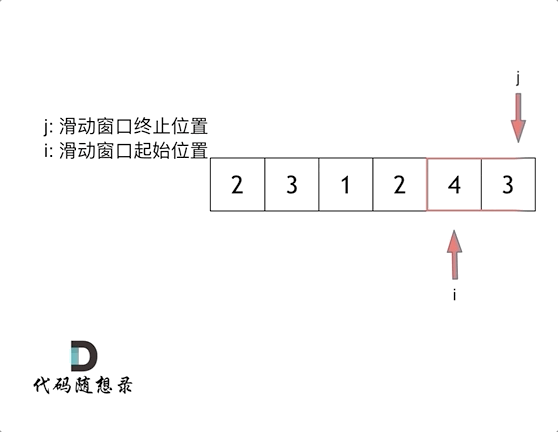
滑动窗口的精妙之处在于根据当前子序列和大小的情况,不断调节子序列的起始位置。从而将O(n^2)暴力解法降为O(n)。
while (sum >= s) {subLength = (j - i + 1); //取子序列的长度result = result < subLength ? result : subLength;这里体现出滑动窗口的精髓之处,不断变更i(子序列的起始位置)sum -= nums[i++]; }
6. 螺旋矩阵II - 模拟
力扣题目链接
题解:【LeetCode-中等】59.螺旋矩阵II - 二维数组
本题并不涉及到什么算法,就是模拟过程,还要注意边界情况。
相关文章:

数据结构与算法 - 数组与二分查找 + Leetcode典型题
1. 什么是数组 数组是存放在连续内存空间上的相同类型数据的集合。 数组可以方便的通过下标索引的方式获取到下标下对应的数据。 C中二维数组在地址空间上也是连续的。 需注意: 数组的下标从0开始。数组内存空间的地址是连续的。数组的元素是不能删的,…...
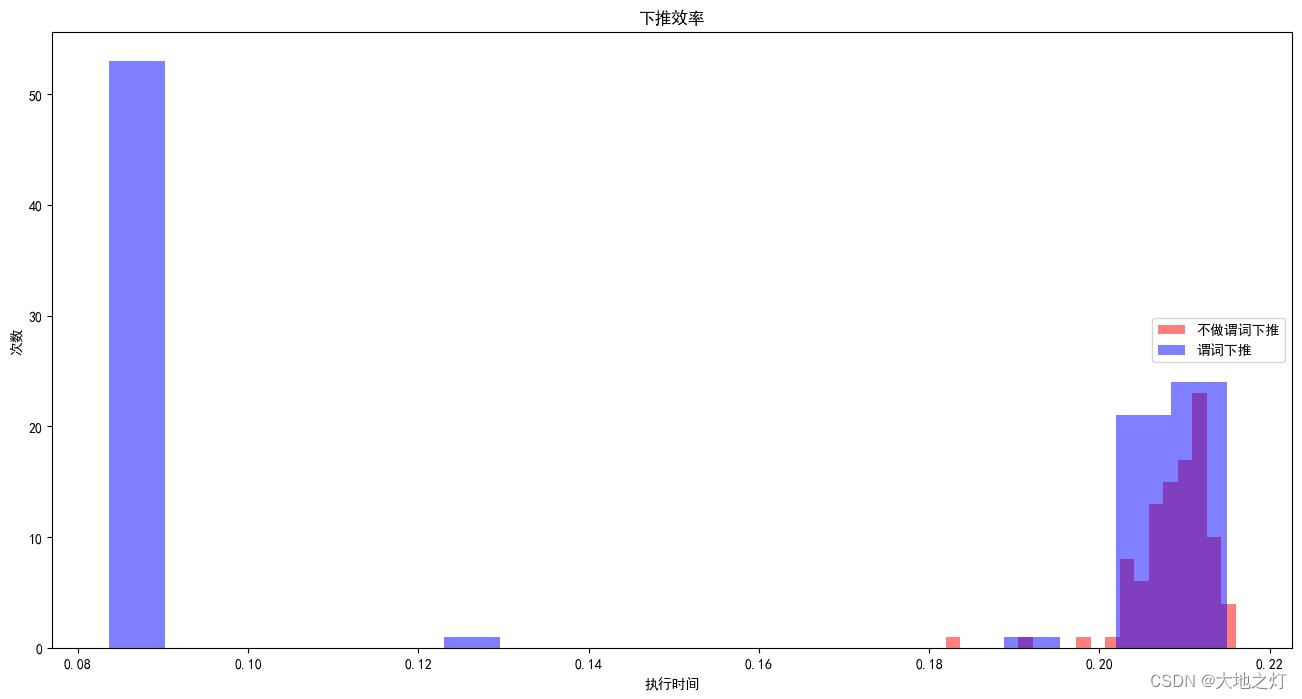
SQL进阶(三):Join 小技巧:提升数据的处理速度
复杂数据结构处理:Join 小技巧:提升数据的处理速度 本文是在原本sql闯关的基础上总结得来,加入了自己的理解以及疑问解答(by GPT4) 原活动链接 用到的数据:链接 提取码:l03e 目录 1. 课前小问…...

开发知识点-.netC#图形用户界面开发之WPF
C#图形用户界面开发 NuGet框架简介WinForms(Windows Forms):WPF(Windows Presentation Foundation):UWP(Universal Windows Platform):MAUI(Multi-platform App UI):选择控件参考文章随笔分类 - WPF入门基础教程系列...
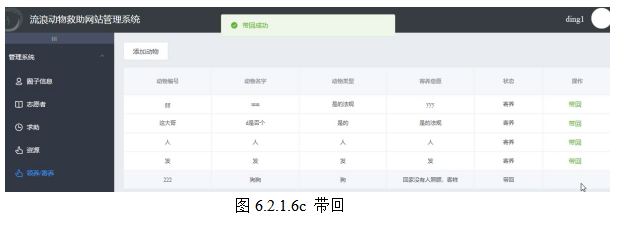
基于springboot实现流浪动物救助网站系统项目【项目源码+论文说明】
基于springboot实现流浪动物救助网站系统演示 摘要 然而随着生活的加快,也使很多潜在的危险日益突显出来,比如在各种地方会发现很多无家可归的、伤痕累累的、可怜兮兮的动物,当碰到这种情况,是否会立马伸出双手去帮助、救助它们&…...

灰度负载均衡和普通负载均衡有什么区别
灰度负载均衡(Gray Load Balancing)与普通负载均衡的主要区别在于它们服务发布和流量管理的方式。 灰度负载均衡 目的:主要用于灰度发布,即逐步向用户发布新版本的服务,以减少新版本可能带来的风险。工作方式&#x…...

【二分查找】朴素二分查找
二分查找 题目描述 给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。 示例 1: 输入: nums [-1,0,3,5,9,12], target 9…...
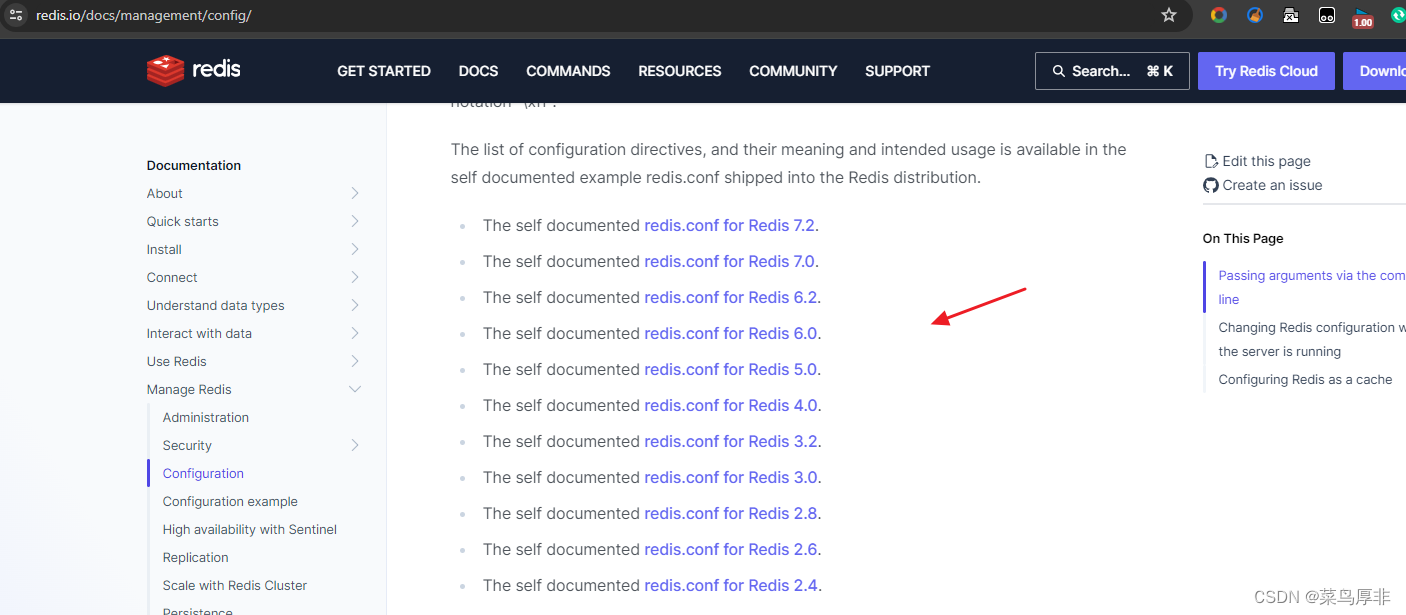
Windows Docker 部署 Redis
部署 Redis 打开 Docker Desktop,切换到 Linux 内核。然后在 PowerShell 执行下面命令,即可启动一个 redis 服务。这里安装的是 7.2.4 版本,如果需要安装其他或者最新版本,可以到 Docker Hub 中进行查找。 docker run -d --nam…...
什么是VR虚拟现实|虚拟科技博物馆|VR设备购买
虚拟现实(Virtual Reality,简称VR)是一种通过计算机技术模拟出的一种全新的人机交互方式。它可以通过专门的设备(如头戴式显示器)将用户带入一个计算机生成的虚拟环境之中,使用户能够与这个虚拟环境进行交互…...

高性能API云原生网关 APISIX安装与配置指南
Apache APISIX是Apache软件基金会下的顶级项目,由API7.ai开发并捐赠。它是一个高性能的云原生API网关,具有动态、实时等特点。 APISIX网关可作为所有业务的流量入口,为用户提供了丰富的功能,包括动态路由、动态上游、动态证书、A…...

Gradio Dataframe 学习笔记
Gradio Dataframe 学习笔记 0. 简介1. 使用场景2. 测试数据3. 学习代码4. 更多功能5. 学习资源6. 总结 0. 简介 Gradio是一个用于构建交互式机器学习界面的Python库。它可以轻松创建各种类型的界面,包括用于数据可视化和探索的界面。 Gradio Dataframe 组件是 Gra…...
深入理解计算机系统笔记
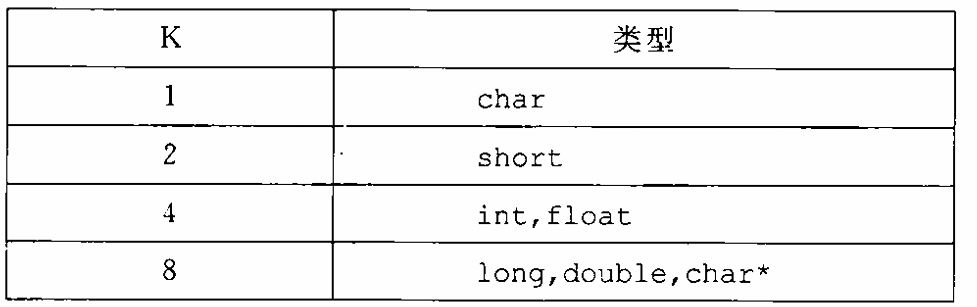
1.1 嵌套的数组 当我们创建数组的数组时,数组分配和引用的一般原则也是成立的。 例如,声明 int A[5][3]; 等价于下面的声明 typedef int row3_t[3]; row3_t A[5] 要访问多维数组的元素,编译器会以数组起始为基地址, (可能需…...
300分钟吃透分布式缓存(拉钩教育总结)
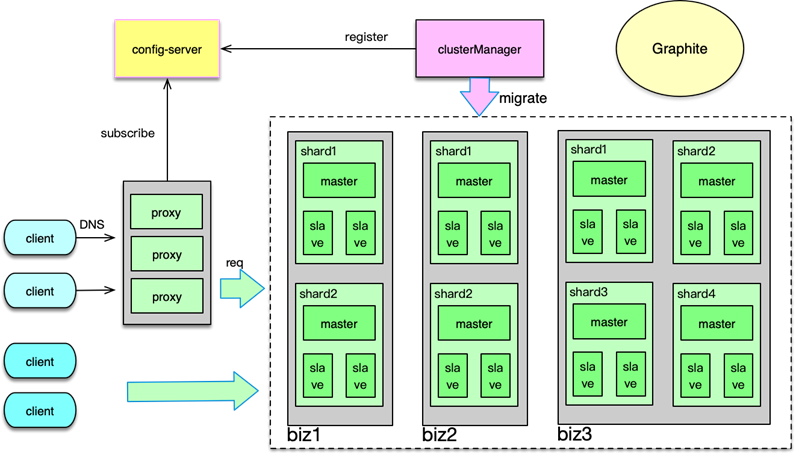
开篇寄语 开篇寄语:缓存,你真的用对了吗? 你好,我是你的缓存老师陈波,可能大家对我的网名 fishermen 会更熟悉。 我是资深老码农一枚,经历了新浪微博从起步到当前月活数亿用户的大型互联网系统的技术演进…...

2024亚马逊全球开店注册前需要准备什么?
在2023年出海四小龙SHEIN、Temu、速卖通AliExpress、TikTok Shop快速增长扩张,成为了中国跨境卖家“逃离亚马逊”的新选择。但是,跨境电商看亚马逊。当前,亚马逊仍然是跨境电商行业的绝对老大,占有将近70%成以上的业务份额。 作为…...
android Service 与 activity 通信 并不断传数据
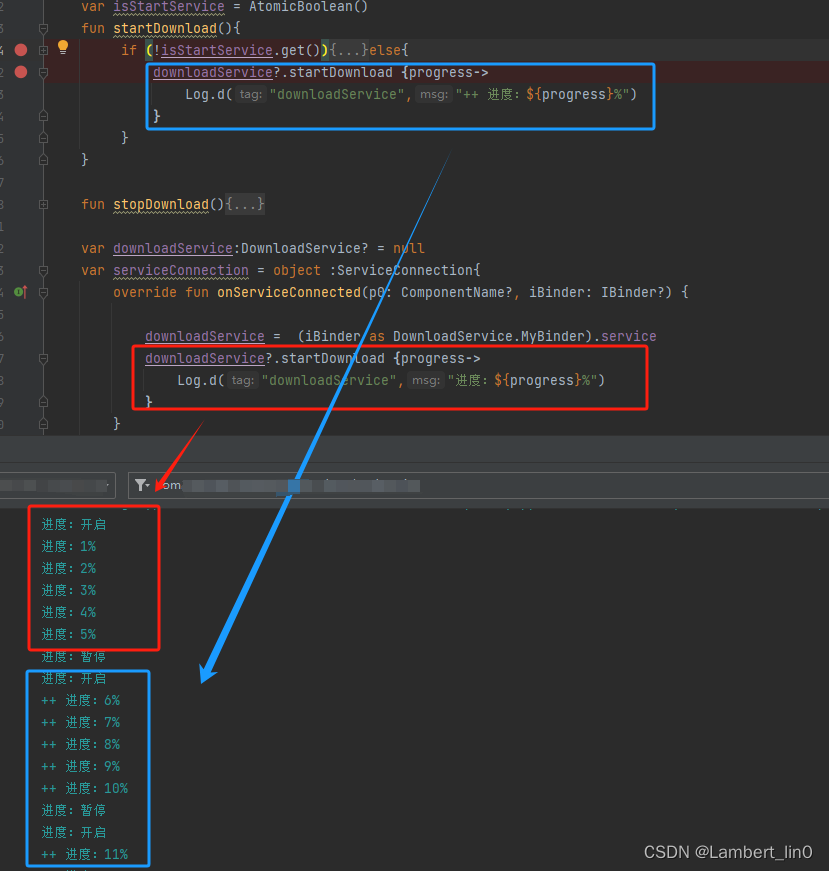
注:这只是个Demo 以下载为案例,实现开启下载,暂停下载,下载进度不断发送给activity class DownloadService : Service() {override fun onBind(intent: Intent?): IBinder? {return MyBinder()}inner class MyBinder : Binder…...
)
Acwing-基础算法课笔记之数学知识(扩展欧几里得算法)
Acwing-基础算法课笔记之数学知识(扩展欧几里得算法) 一、扩展欧几里得算法1、裴蜀定理2、过程模拟3、代码模板 二、线性同余方程1、定义2、模拟过程3、结论证明 一、扩展欧几里得算法 1、裴蜀定理 对于任意正整数 a a a, b b b࿰…...
)
简单排列组合题(python版)
文章预览: 题目解法一输出结果 解法二输出结果输出结果 题目 有四个数字:1,2,3,4能组成多少个互不相同且无重复的数字的三位数? 各式多少? 解法一 我们粗略看一下这个题既然我们要组成三位数,那我们就循环3层每一层出一个数,并且if语句判…...

【排坑】搭建 Karmada 环境
git clone 报错 问题:Failed to connect to github.com port 443:connection timed out 解决: git config --global --unset http.proxy【hack/local-up-karmada.sh】 1. karmada ca-certificates (no such package) 问题:fetching http…...

每日一类:Qt GUI开发的基石《QWidget》
深入探索QWidget:Qt GUI开发的基石 在Qt框架中,QWidget类扮演着构建图形用户界面(GUI)的基础角色。它不仅提供了窗口的基本功能,还允许开发者通过继承和定制来创建各式各样的用户界面元素。本文将详细介绍QWidget的关…...
人大金仓与mysql的差异与替换
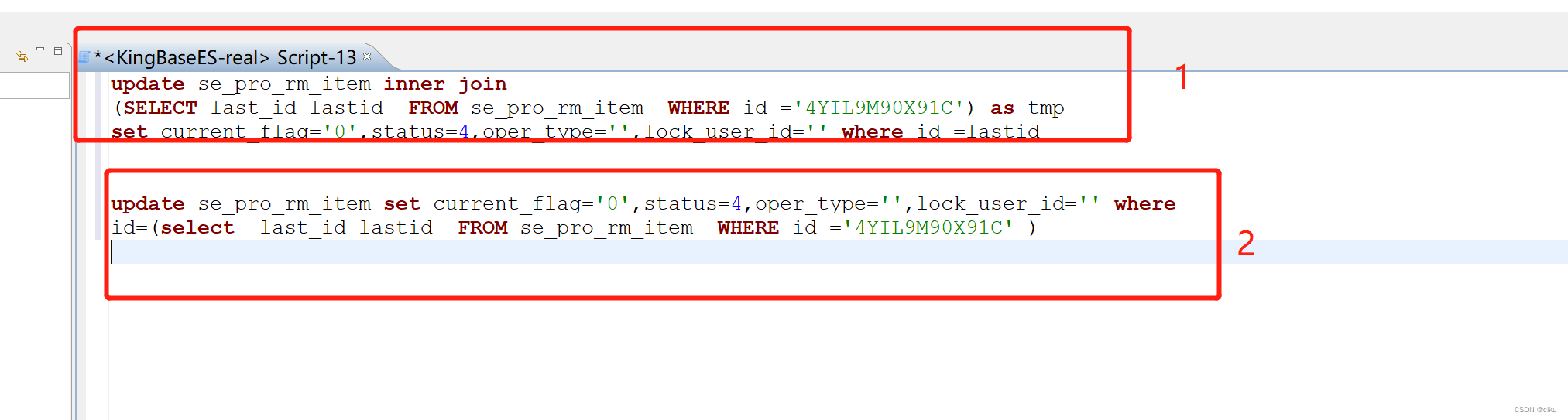
人大金仓中不能使用~下面的符号,字段中使用”,无法识别建表语句 创建表时语句中只定义字段名.字段类型.是否是否为空 Varchar类型改为varchar(长度 char) Int(0) 类型为int4 定义主键:CONSTRAINT 键名 主键类型&#x…...
Excel2LaTeX插件的使用、LaTeX表格
目录 一、下载Excel2Latex 二、使用Excel2Latex 1、将Excel2LaTeX文件添加到加载项 2、导出LaTex的表格数据 3、注意事项 1)生成的latex表格断断续续问题 2)改变线形的粗细 3)表格太大,需要缩小到适应大小 4)…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...
