MySQL 逗号分隔查询--find_in_set()函数
业务场景:
在使用MySQL的时候,可能的某个字段存储的是一个英文逗号分割的字符串(这里我们不讨论表设计的合理性),如图所示:

我们在查询的时候需要匹配逗号分割中的某个字符串,该怎么查询呢?
find_in_set函数:
函数结构:find_in_set(str,strlist)
- str:要查询的字符串。
- strlist: 字段名,示例中的 business_line_reviewer 字段。
为了方便理解,我们可以认为strlist是由多个str且以英文逗号分割组成的,函数返回的是str在strlist中的位置,返回值的范围在 1 到 N 之间,需要注意的是strlist不能以英文逗号开头。
find_in_set函数用法演示:
select id,business_line_reviewer from org_performance_approver where find_in_set('zt19379', business_line_reviewer) > 0
查询结果:

完美解决了在查询的时候需要匹配逗号分割中的某个字符串的场景。
索引使用情况:
explain select business_line_reviewer from org_performance_approver where find_in_set('zt19379', business_line_reviewer) > 0;

MySQL版本
select version();

总结:
在查阅资料寻求解决方案的时候,看到部分资料说 find_in_set 函数不支持英文逗号分割 ,我使用的 8.0.27 版本是支持的,可能是老版本不支持,这个待求证,也有资料 find_in_set 函数说不支持索引,同样我在使用的时候看了执行计划,也是支持索引的,可能也是老版本不支持。
如有不正确的地方请各位指出纠正。
相关文章:

MySQL 逗号分隔查询--find_in_set()函数
业务场景: 在使用MySQL的时候,可能的某个字段存储的是一个英文逗号分割的字符串(这里我们不讨论表设计的合理性),如图所示: 我们在查询的时候需要匹配逗号分割中的某个字符串,该怎么查询呢&am…...

【物联网应用案例】智能农业的 9 个技术用例
一、农业中的物联网用例 一般而言,农业物联网传感器以及农业物联网应用有多种类型: 1. 气候条件监测 气象站无疑是当今智能农业领域最受欢迎的设备。这款设备集成了多种智能农业传感器,能够在现场对各类数据进行收集,然后迅速将…...

前端开发——ElementUI组件的使用
文章目录 1. Tabs标签页2. 单选框 el-radio3. 复选框 el-checkbox4. 下拉框 el-select5. 表格 el-table6. 对话框 el-dialog7. 文字提示 el-tooltip8. 抽屉 el-drawer 1. Tabs标签页 <template><el-tabs v-model"activeName" tab-click"handleClick&q…...

Unity编写Shader内置各种矩阵和方法介绍
嗨,各位小伙伴们,我是你们的好朋友咕噜铁蛋!今天,我们要来聊一聊关于Unity中编写Shader时内置的各种矩阵和方法。作为Unity开发者,掌握Shader编写是非常重要的一项技能,而了解内置的矩阵和方法将帮助我们更…...
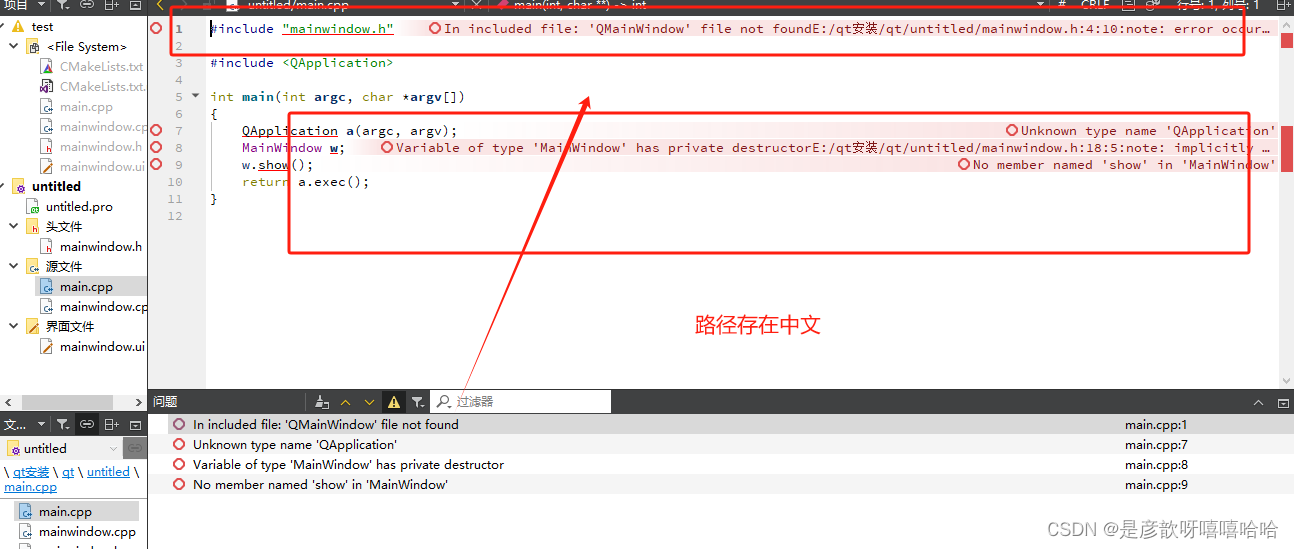
初学者如何使用QT新建一个包含UI界面的C++项目
文章目录 一、下载并安装QT51、下载安装包2、注册/登录账号3、安装qt6 二、新建QT Widget项目1、新建项目并且运行2、易错点:可能运行成功得到UI界面但是会报错(原因是使用了中文路径) 一、下载并安装QT5 1、下载安装包 进入下载网址 Windo…...

韦东山嵌入式Liunx入门驱动开发四
文章目录 一、异常与中断的概念及处理流程1-1 中断的引入1-2 栈(1) CPU实现a ab的过程(2) 进程与线程 1-3 Linux系统对中断处理的演进1-4 Linux 中断系统中的重要数据结构(1) irq_desc 结构体(2) irqaction 结构体(3) irq_data 结构体(4) irq_domain 结构体(5) irq_domain 结构…...
ubuntu基础操作(1)-个人笔记
搜狗输入法Linux官网-首页搜狗输入法for linux—支持全拼、简拼、模糊音、云输入、皮肤、中英混输https://pinyin.sogou.com/linux 1.关闭sudo密码: 终端(ctrl alt t)输入 sudo visudo 打开visudo 找到 %sudo ALL(ALL:ALL) ALL 这一行…...
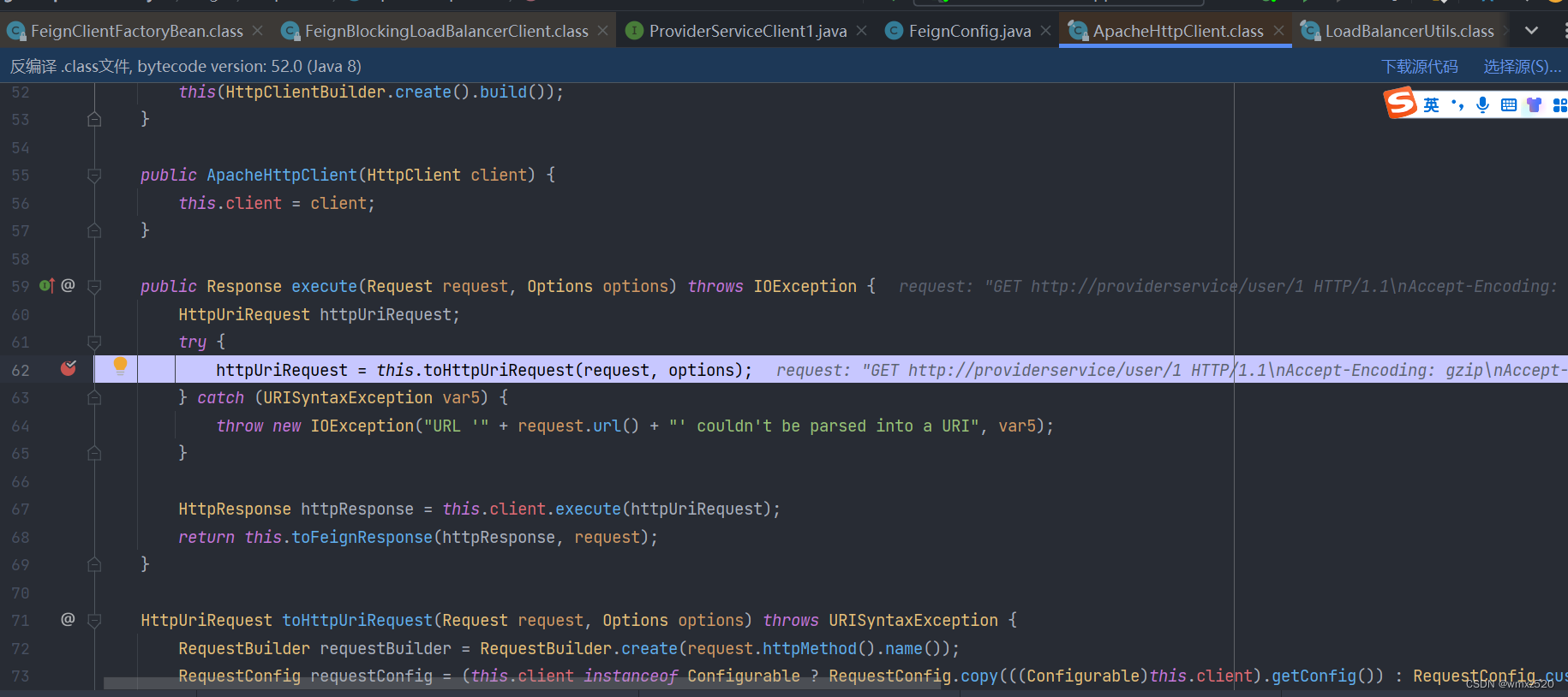
Spring Cloud2022之OpenFeign使用以及部分源码分析
OpenFeign使用 Feign和OpenFeign Feign是Netflix开发的⼀个轻量级RESTful的HTTP服务客户端,可以使用⽤它来发起请求,进行远程调用。Fegin是以Java接口注解的⽅式调⽤Http请求,而不是像RestTemplate那样,在Java中通过封装HTTP请求…...

【非比较排序】计算排序算法
目录 CountSort计数排序 整体思想 图解分析 代码实现 时间复杂度&优缺分析 CountSort计数排序 计数排序是一种非比较排序,不需要像前面的排序一样去比较。 计数排序的特性总结: 1. 计数排序在数据范围集中时,效率很高,但…...
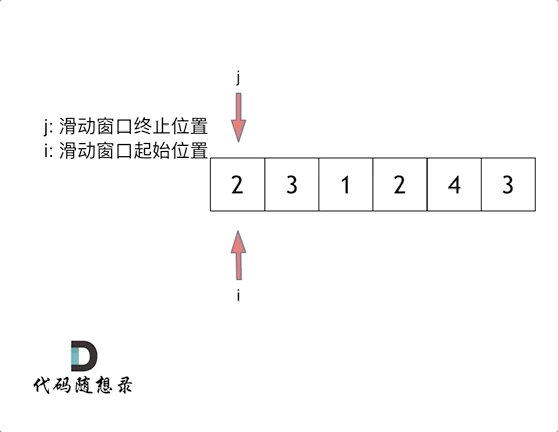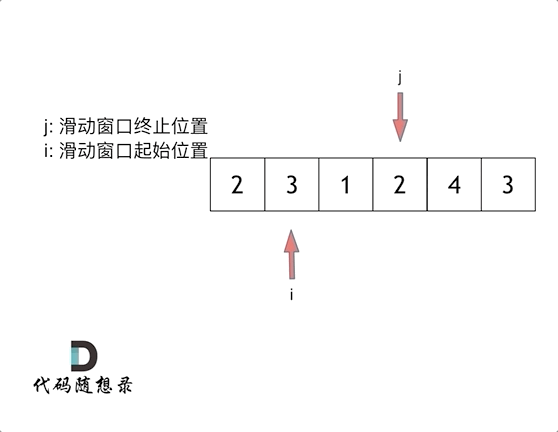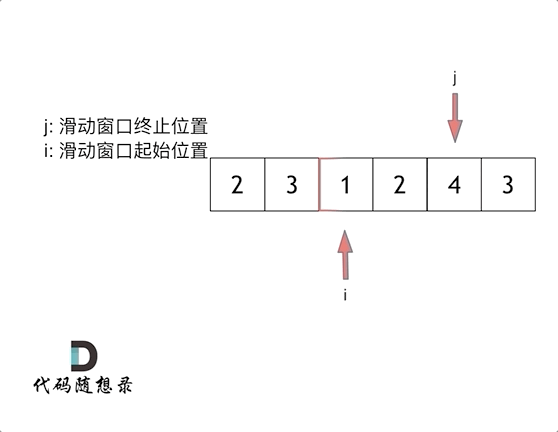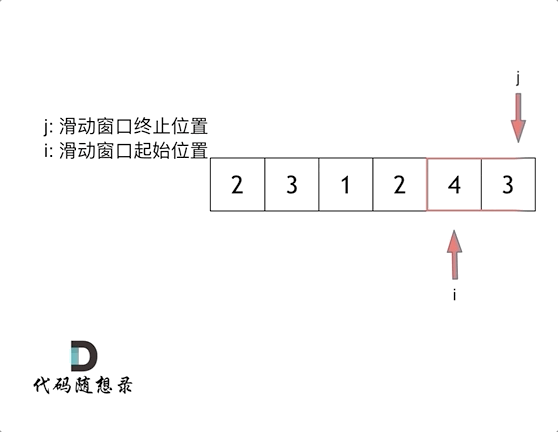
数据结构与算法 - 数组与二分查找 + Leetcode典型题
1. 什么是数组 数组是存放在连续内存空间上的相同类型数据的集合。 数组可以方便的通过下标索引的方式获取到下标下对应的数据。 C中二维数组在地址空间上也是连续的。 需注意: 数组的下标从0开始。数组内存空间的地址是连续的。数组的元素是不能删的,…...
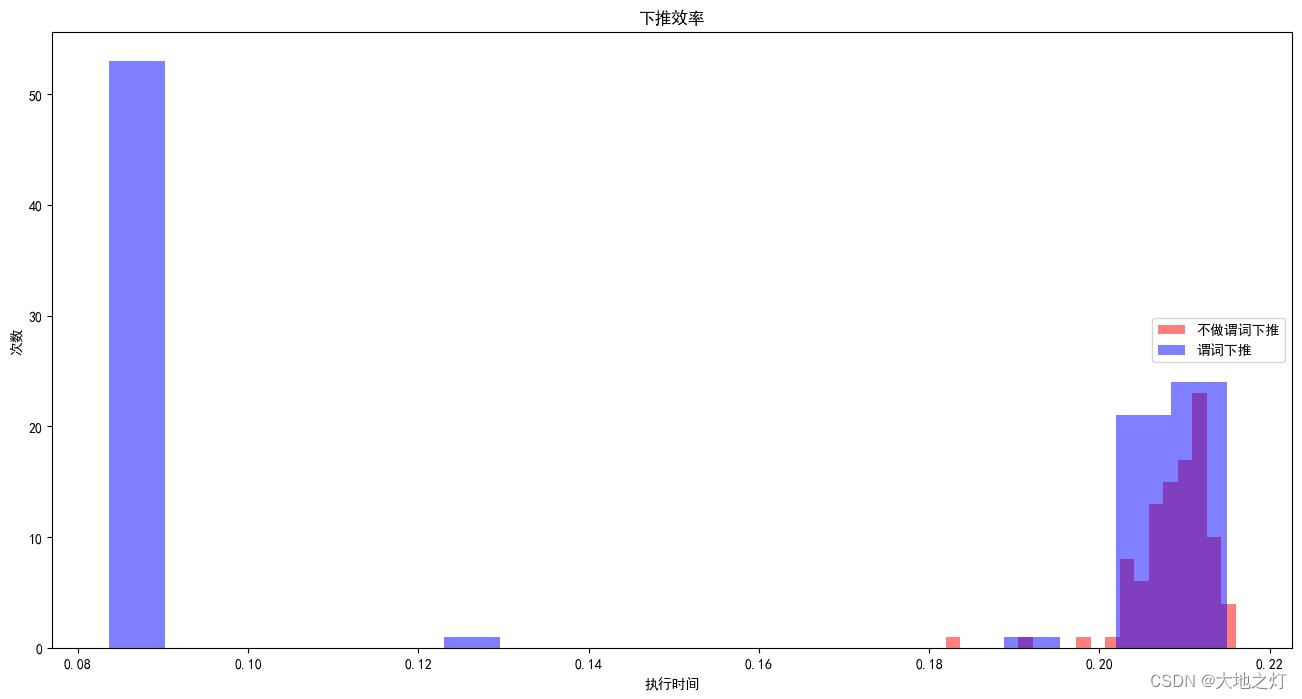
SQL进阶(三):Join 小技巧:提升数据的处理速度
复杂数据结构处理:Join 小技巧:提升数据的处理速度 本文是在原本sql闯关的基础上总结得来,加入了自己的理解以及疑问解答(by GPT4) 原活动链接 用到的数据:链接 提取码:l03e 目录 1. 课前小问…...

开发知识点-.netC#图形用户界面开发之WPF
C#图形用户界面开发 NuGet框架简介WinForms(Windows Forms):WPF(Windows Presentation Foundation):UWP(Universal Windows Platform):MAUI(Multi-platform App UI):选择控件参考文章随笔分类 - WPF入门基础教程系列...
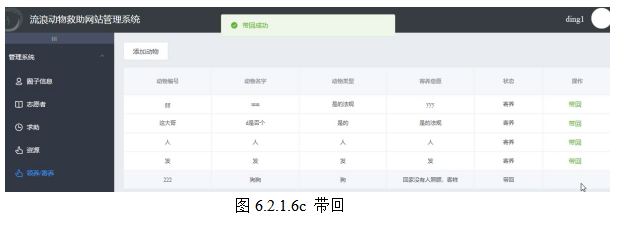
基于springboot实现流浪动物救助网站系统项目【项目源码+论文说明】
基于springboot实现流浪动物救助网站系统演示 摘要 然而随着生活的加快,也使很多潜在的危险日益突显出来,比如在各种地方会发现很多无家可归的、伤痕累累的、可怜兮兮的动物,当碰到这种情况,是否会立马伸出双手去帮助、救助它们&…...

灰度负载均衡和普通负载均衡有什么区别
灰度负载均衡(Gray Load Balancing)与普通负载均衡的主要区别在于它们服务发布和流量管理的方式。 灰度负载均衡 目的:主要用于灰度发布,即逐步向用户发布新版本的服务,以减少新版本可能带来的风险。工作方式&#x…...

【二分查找】朴素二分查找
二分查找 题目描述 给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。 示例 1: 输入: nums [-1,0,3,5,9,12], target 9…...
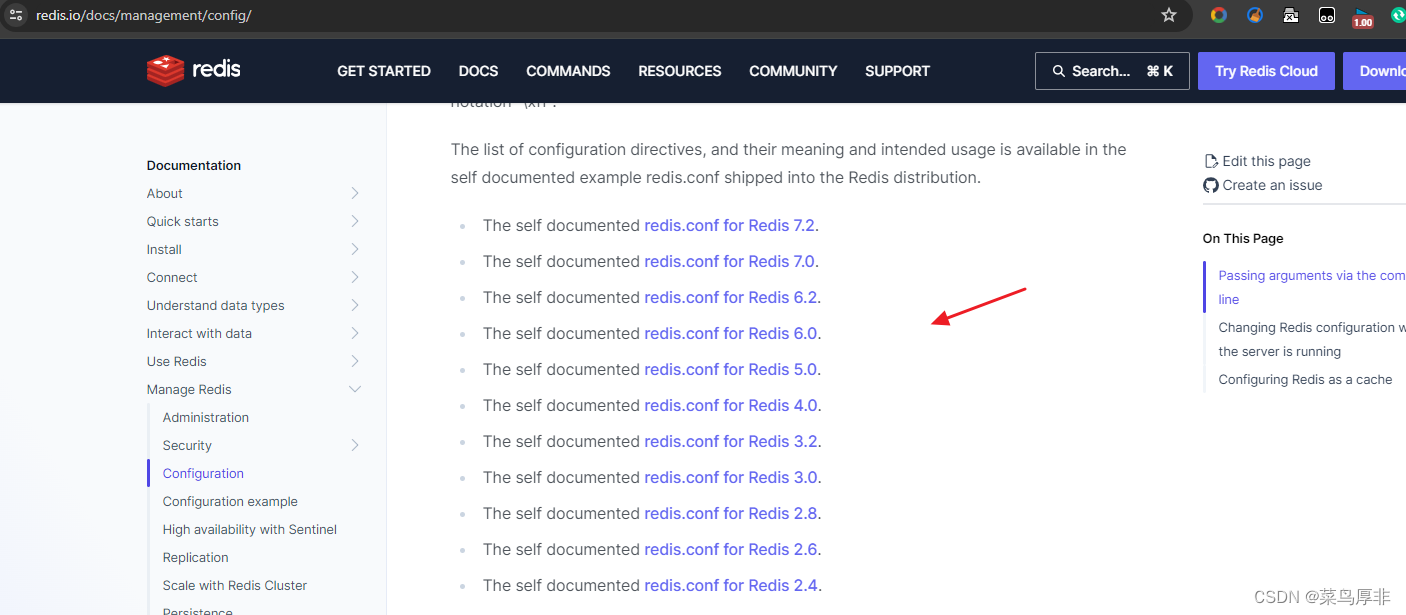
Windows Docker 部署 Redis
部署 Redis 打开 Docker Desktop,切换到 Linux 内核。然后在 PowerShell 执行下面命令,即可启动一个 redis 服务。这里安装的是 7.2.4 版本,如果需要安装其他或者最新版本,可以到 Docker Hub 中进行查找。 docker run -d --nam…...
什么是VR虚拟现实|虚拟科技博物馆|VR设备购买
虚拟现实(Virtual Reality,简称VR)是一种通过计算机技术模拟出的一种全新的人机交互方式。它可以通过专门的设备(如头戴式显示器)将用户带入一个计算机生成的虚拟环境之中,使用户能够与这个虚拟环境进行交互…...

高性能API云原生网关 APISIX安装与配置指南
Apache APISIX是Apache软件基金会下的顶级项目,由API7.ai开发并捐赠。它是一个高性能的云原生API网关,具有动态、实时等特点。 APISIX网关可作为所有业务的流量入口,为用户提供了丰富的功能,包括动态路由、动态上游、动态证书、A…...

Gradio Dataframe 学习笔记
Gradio Dataframe 学习笔记 0. 简介1. 使用场景2. 测试数据3. 学习代码4. 更多功能5. 学习资源6. 总结 0. 简介 Gradio是一个用于构建交互式机器学习界面的Python库。它可以轻松创建各种类型的界面,包括用于数据可视化和探索的界面。 Gradio Dataframe 组件是 Gra…...
深入理解计算机系统笔记
1.1 嵌套的数组 当我们创建数组的数组时,数组分配和引用的一般原则也是成立的。 例如,声明 int A[5][3]; 等价于下面的声明 typedef int row3_t[3]; row3_t A[5] 要访问多维数组的元素,编译器会以数组起始为基地址, (可能需…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

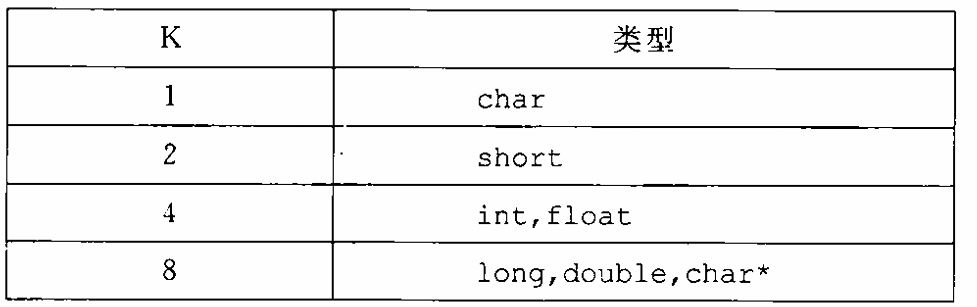
练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...
