当前位置： 首页 > news >正文

3dgs学习（二）—— 3d高斯与协方差矩阵及其几何意义

news 2026/2/8 19:44:01

协方差矩阵与3d高斯

3d高斯与椭球与协方差矩阵

3d高斯，及3维空间内的正态分布。
通过一元正态分布的坐标系图像不难想象，3维空间中的正态分布点集中在一片椭球空间中，各方向长轴取决于各方向正态分布的方差。
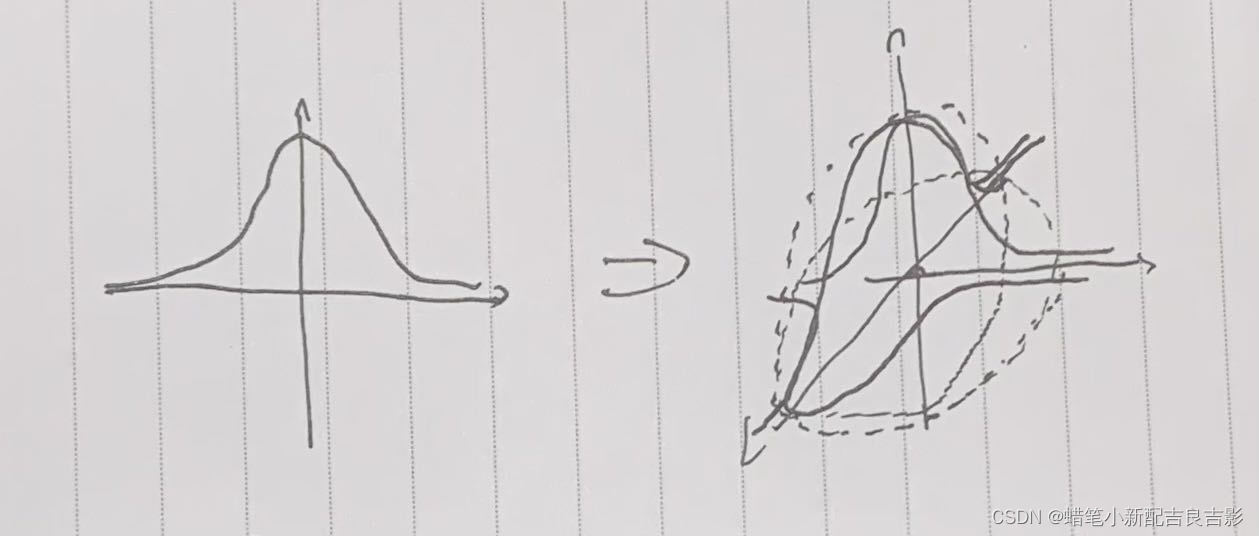
在这里插入图片描述

而协方差矩阵通过计算多元之间的协方差关系，反映了椭球在空间中所呈现的几何形态，具体表现方法见下文。

协方差矩阵的几何意义

参考文章：https://www.zhihu.com/tardis/zm/art/37609917?source_id=1005

  • 多元正态分布函数表达式如下：
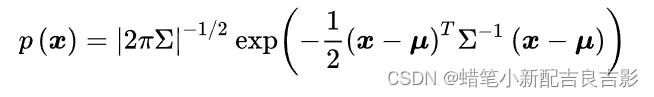
    在这里插入图片描述
  • 可简化为：（忽略常数，μ为0）
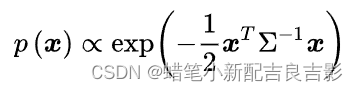
    在这里插入图片描述
  • 考虑线性变换 t = Mx
  • 引入缩放矩阵S

3维空间中则在3个轴上进行缩放，需要一个3*3*3的对角线矩阵

在这里插入图片描述

  • 引入旋转矩阵R
    在这里插入图片描述
  • 通过左乘变换矩阵的规则可知，变化矩阵M = RS
  • 又x = M⁻¹t，通过带入化简后的多元正态分布表达式，可以得到
    ∑ = MMᵀ
  • 综上可以得到 ∑ = RSSᵀRᵀ
    即得到协方差函数所表示的放缩/旋转几何意义
    对应该放缩/旋转操作所得到的空间内唯一形状的椭球
    及对应唯一的一组3d高斯表达。
  • 这样的变换会在后面的加快参数更新中得到应用

相关文章：

3dgs学习（二）—— 3d高斯与协方差矩阵及其几何意义

协方差矩阵与3d高斯 3d高斯与椭球与协方差矩阵 3d高斯，及3维空间内的正态分布。 通过一元正态分布的坐标系图像不难想象，3维空间中的正态分布点集中在一片椭球空间中，各方向长轴取决于各方向正态分布的方差。 而协方差矩阵通过计算多元之…...

编程日记 2024/3/1 19:43:04

ZStack Cube超融合入选IDC《中国超融合基础架构市场评估》报告

近日，IDC发布了《中国超融合基础架构市场评估，2023》。IDC针对中国超融合基础架构市场的发展现状展开了调研，明确了最终用户构建融合型云平台的痛点和难点，阐述了市场中各技术服务提供商的服务方案和优势，并对未来中国…...

编程日记 2024/3/1 19:42:03

每日一题——LeetCode1556.千位分隔符

方法一 个人方法： 把n转为字符串，逆序遍历n，把n的每个元素加入res，每三次加入.，最后将res翻转再转为字符串即为符合题目要求的结果 var thousandSeparator function(n) {nlet res[],lenn.length-1for(let ilen;i>…...

编程日记 2024/3/1 19:40:02

8.网络游戏逆向分析与漏洞攻防-游戏网络架构逆向分析-游戏底层功能对接类GameProc的实现

内容参考于：易道云信息技术研究院VIP课 上一个内容：通过逆向分析确定游戏明文接收数据过程 码云地址（master 分支）：https://gitee.com/dye_your_fingers/titan 码云版本号：bcf7559184863febdcad819e48aa…...

编程日记 2024/3/1 19:39:01

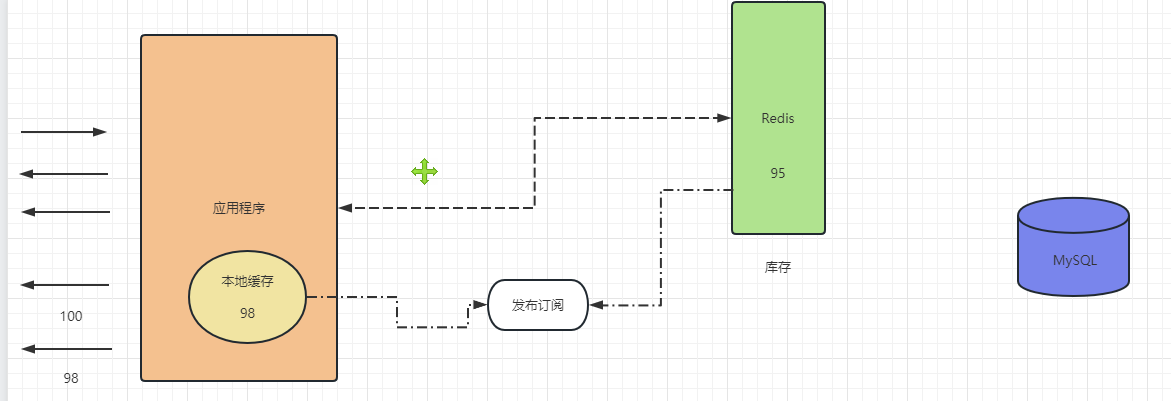
Redis冲冲冲——事务支持，AOF和RDB持久化

目录 引出Redis事务支持，AOF和RDB持久化1、Redis的事务支持2、Redis的持久化 Redis冲冲冲——缓存三兄弟：缓存击穿、穿透、雪崩缓存击穿缓存穿透缓存雪崩 总结 引出 Redis冲冲冲——事务支持，AOF和RDB持久化 Redis事务支持，AOF和…...

编程日记 2024/3/1 19:37:59

路由菜单路径匹配方法

优化路由菜单路径匹配算法：实现获取整条线路的路径 引言 在前端开发中，路由菜单的路径匹配是一个常见的需求。我们经常需要根据给定的路径，找到对应的菜单项，并获取整条线路的路径。本文将介绍一个优化的路由菜单路径匹配算法&…...

编程日记 2024/3/1 19:35:57

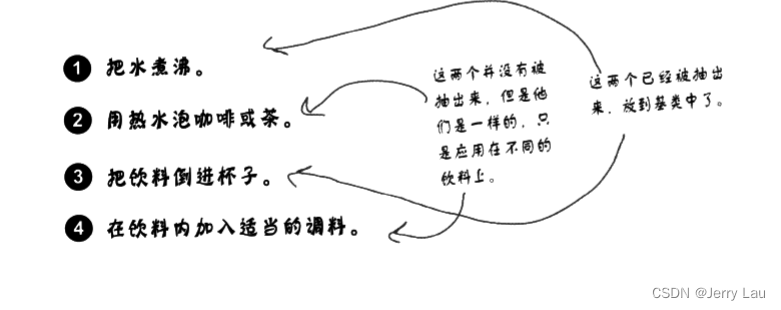
设计模式浅析(九) ·模板方法模式

设计模式浅析(九) 模板方法模式 日常叨逼叨 java设计模式浅析，如果觉得对你有帮助，记得一键三连，谢谢各位观众老爷😁😁 模板方法模式 概念 模板方法模式（Template Method Pattern）在Java中是…...

编程日记 2024/3/1 19:34:56

无用工作、UBI与AI

有些隐晦和黑暗的事实无法陈述，因为任何的系统中“无用”的结局都是被无情的抛弃和淘汰，AI监督下的人类结局更是如此。 什么是无用工作？ 无用无效工作通常指的是那些看似忙碌但实际上对社会或个人没有实质性贡献的工作。这类工作可能包括以下…...

编程日记 2024/3/1 19:33:56

【监控】grafana图表使用快速上手

目录 1.前言 2.连接 3.图表 4.job和path 5.总结 1.前言 上一篇文章中，我们使用spring actuatorPrometheusgrafana实现了对一个spring boot应用的可视化监控。 【监控】Spring BootPrometheusGrafana实现可视化监控-CSDN博客 其中对grafana只是打开了一下&am…...

编程日记 2024/3/1 19:31:54

Django常用命令

一、新建一个新项目 django-admin startproject project_name二、新建一个app 在Django中的一个app代表一个功能模块。开发者可以将不同功能的模块放在不同的app中, 方便代码的复用。 python manage.py startapp appa_name三、数据迁移(更新数据库) 编写好了Model后&#x…...

编程日记 2024/3/1 19:30:53

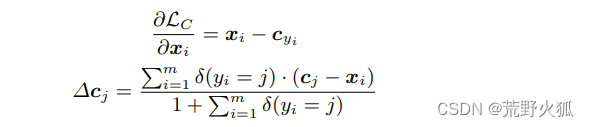
【center-loss 中心损失函数】 原理及程序解释（更新中）

文章目录 前言问题引出open-set问题抛出 解决方法softmax函数、softmax-loss函数解决代码（center_loss.py）原理程序解释 如何梯度更新首先了解一下基本的梯度下降算法然后 前言 学习一下： 中心损失函数，用于用于深度人脸识别的特…...

编程日记 2024/3/1 19:29:52

什么是 HTTPS 证书？作用是什么？

HTTPS 证书，即超文本传输安全协议证书（Hypertext Transfer Protocol Secure），是网站安全的关键组成部分。它通过 SSL/TLS 加密协议，确保用户与网站之间的数据传输是加密和安全的。 什么是 HTTPS 证书？ HT…...

编程日记 2024/3/1 19:26:49

为什么软考报名人数越来越多？

2020年软考报名人数404666人，广东省报考人数超过14万人。 ●2021年软考通信考试报名人数突破100万人，估计软考有90多万。 ●2022年软考通信考试共129万人，估计软考占了120多万人。 ●2023年软考具体报名人数没有公布，但工业和信…...

编程日记 2024/3/1 19:25:48

【投稿优惠|快速见刊】2024年图像，机器学习和人工智能国际会议（ICIMLAI 2024）

【投稿优惠|快速见刊】2024年图像，机器学习和人工智能国际会议（ICIMLAI 2024） 重要信息 会议官网：http://www.icimlai.com会议地址：深圳召开日期：2024.03.30截稿日期：2024.03.20 （先…...

编程日记 2024/3/1 19:23:45

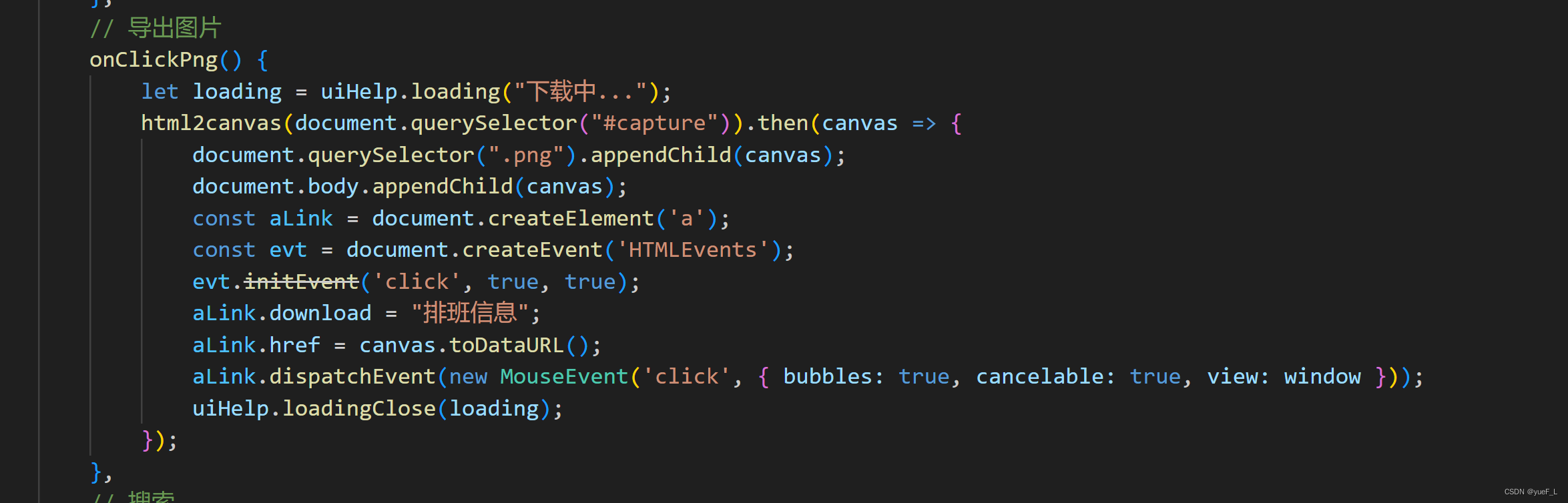
html2canvas 将DOM节点转成图片

官网地址：html2canvas - Screenshots with JavaScript 将js文件保存到本地 可以新建一个txt文件，然后丢进去修改后缀名称即可。 在项目中引入js文件： import html2canvas from "../html2canvas.min.js" 这是我准备画的DOM节点。…...

编程日记 2024/3/1 19:21:43

【多线程】常见锁策略详解（面试常考题型）

目录 🌴 乐观锁 vs 悲观锁🎍重量级锁 vs 轻量级锁🍀自旋锁（Spin Lock）🎋公平锁 vs ⾮公平锁🌳可重⼊锁 vs 不可重⼊锁🎄读写锁⭕相关面试题 常⻅的锁策略 注意: 接下来讲解的锁策略不…...

编程日记 2024/3/1 19:20:42

Python列表操作函数

在Python中，列表（list）是一种可变的数据类型，它包含一系列有序的元素。Python提供了一系列内置的函数和方法来操作列表。以下是一些常用的Python列表操作函数和方法： 列表方法 append(x) 将元素x添加到列表的末尾。 …...

编程日记 2024/3/1 19:19:41

Qt注册类对象单例与单类型区别

1.实现类型SingletonTypeExample #ifndef SINGLETONTYPEEXAMPLE_H #define SINGLETONTYPEEXAMPLE_H#include <QObject>class SingletonTypeExample : public QObject {Q_OBJECT public://只能显示构造类对象explicit SingletonTypeExample(QObject *parent nullptr);//…...

编程日记 2024/3/1 19:17:40

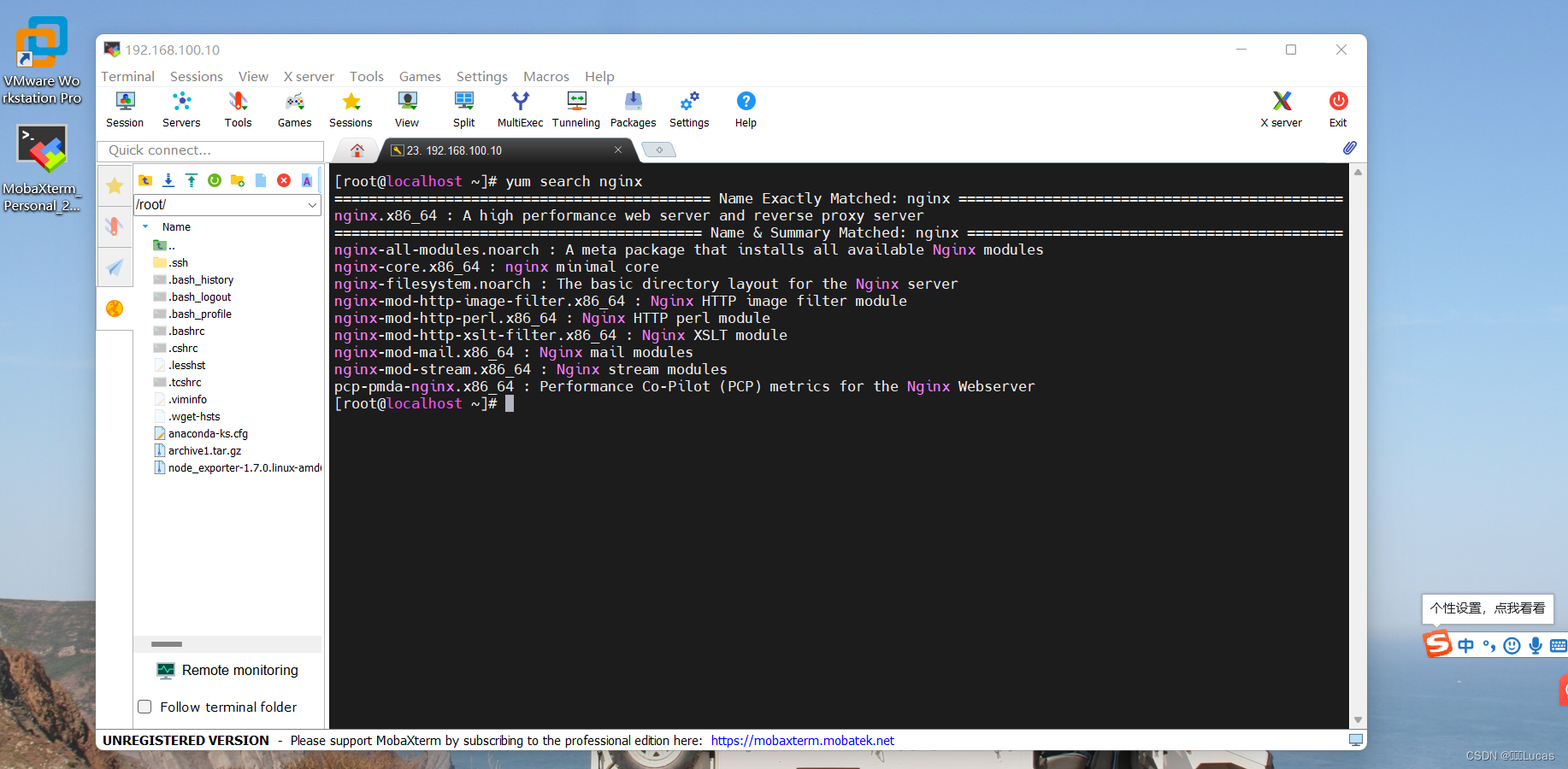
Rocky Linux 运维工具yum

一、yum的简介 ​​yum​是用于在基于RPM包管理系统的包管理工具。用户可以通过 ​yum​来搜索、安装、更新和删除软件包&#xff0c;自动处理依赖关系&#xff0c;方便快捷地管理系统上的软件。 二、yum的参数说明 1、install 用于在系统的上安装一个或多个软件包 2、seach 用…...

编程日记 2024/3/1 19:14:37

linux下的ollama

refs: https://github.com/ollama/ollama/blob/main/docs/linux.md 1)安装 curl -fsSL https://ollama.com/install.sh | sh 2)修改服务配置&#xff0c;打开端口允许所有IP地址 refs(https://github.com/ollama/ollama/blob/main/docs/faq.md#where-are-models-stored) C…...

编程日记 2024/3/1 19:13:37

1.3 VSCode安装与环境配置

进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件&#xff0c;然后打开终端&#xff0c;进入下载文件夹&#xff0c;键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

编程新知 2026/1/29 3:35:37

python爬虫：Newspaper3k 的详细使用（好用的新闻网站文章抓取和解析的Python库）

更多内容请见： 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

编程新知 2025/10/25 7:51:48

Python爬虫（一）：爬虫伪装

一、网站防爬机制概述 在当今互联网环境中&#xff0c;具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类&#xff1a; 身份验证机制&#xff1a;直接将未经授权的爬虫阻挡在外反爬技术体系&#xff1a;通过各种技术手段增加爬虫获取数据的难度…...

编程新知 2026/1/30 20:42:46

论文阅读：LLM4Drive: A Survey of Large Language Models for Autonomous Driving

地址&#xff1a;LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂&#xff0c;正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

编程新知 2026/2/4 4:39:19

深度剖析 DeepSeek 开源模型部署与应用：策略、权衡与未来走向

在人工智能技术呈指数级发展的当下&#xff0c;大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性&#xff0c;吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型&#xff0c;成为释放其巨大潜力的关键所在&…...

编程新知 2025/12/27 19:12:07

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程（6.3）

目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 ​编辑​编辑 UDP的特征 socke函数 bind函数 recvfrom函数&#xff08;接收函数&#xff09; sendto函数&#xff08;发送函数&#xff09; 五、网络编程之 UDP 用…...

编程新知 2026/2/6 5:57:59

ZYNQ学习记录FPGA(一)ZYNQ简介

一、知识准备 1.一些术语,缩写和概念&#xff1a; 1&#xff09;ZYNQ全称&#xff1a;ZYNQ7000 All Pgrammable SoC 2&#xff09;SoC:system on chips(片上系统)&#xff0c;对比集成电路的SoB&#xff08;system on board&#xff09; 3&#xff09;ARM&#xff1a;处理器…...

编程新知 2026/2/5 9:30:45

算术操作符与类型转换：从基础到精通

目录 前言&#xff1a;从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符&#xff1a;、-、*、/、% 赋值操作符&#xff1a;和复合赋值 单⽬操作符&#xff1a;、--、、- 前言&#xff1a;从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

编程新知 2026/2/5 4:00:38

字符串哈希+KMP

P10468 兔子与兔子 #include<bits/stdc.h> using namespace std; typedef unsigned long long ull; const int N 1000010; ull a[N], pw[N]; int n; ull gethash(int l, int r){return a[r] - a[l - 1] * pw[r - l 1]; } signed main(){ios::sync_with_stdio(false), …...

编程新知 2025/12/13 5:58:57

前端工具库lodash与lodash-es区别详解

lodash 和 lodash-es 是同一工具库的两个不同版本&#xff0c;核心功能完全一致&#xff0c;主要区别在于模块化格式和优化方式&#xff0c;适合不同的开发环境。以下是详细对比&#xff1a; 1. 模块化格式 lodash 使用 CommonJS 模块格式&#xff08;require/module.exports&a…...

编程新知 2025/12/16 16:11:02