c语言经典测试题8
在c语言经典测试题6的第一题,大家是否想过可不可以将递归参数改为s++呢?或许有的人已经试过了,但是发现好像不会有结果,其实是因为s++为后置++,先试用后加1,然而我们这个++是在s出了函数之后才会运行加1操作,又由于该函数为递归函数,不会直接出函数,所以该递归参数就一直是s不会改变,这样的话,代码就会陷入死递归。
1.题1
char ch;
int i;
float f;
double d;
如上图我们定义了4种类型的数据,则表达式: ch/i + (f*d – i) 的结果类型为?
其实在不同类型的数据进行计算时,会统一进行向最高级类型的转换,在这里基本数据类型的等级从低到高如下:char int long float double运算的时候是从低转到高的,表达式的类型会自动提升或者转换为参与表达式求值的最上级类型。所以该表达式的结果类型应该为double类型。
2.题2
#include <stdio.h>
int main()
{
int x = -1;
unsigned int y = 2;
if (x > y)
{
printf("x is greater");
}
else
{
printf("y is greater");
}
return 0;
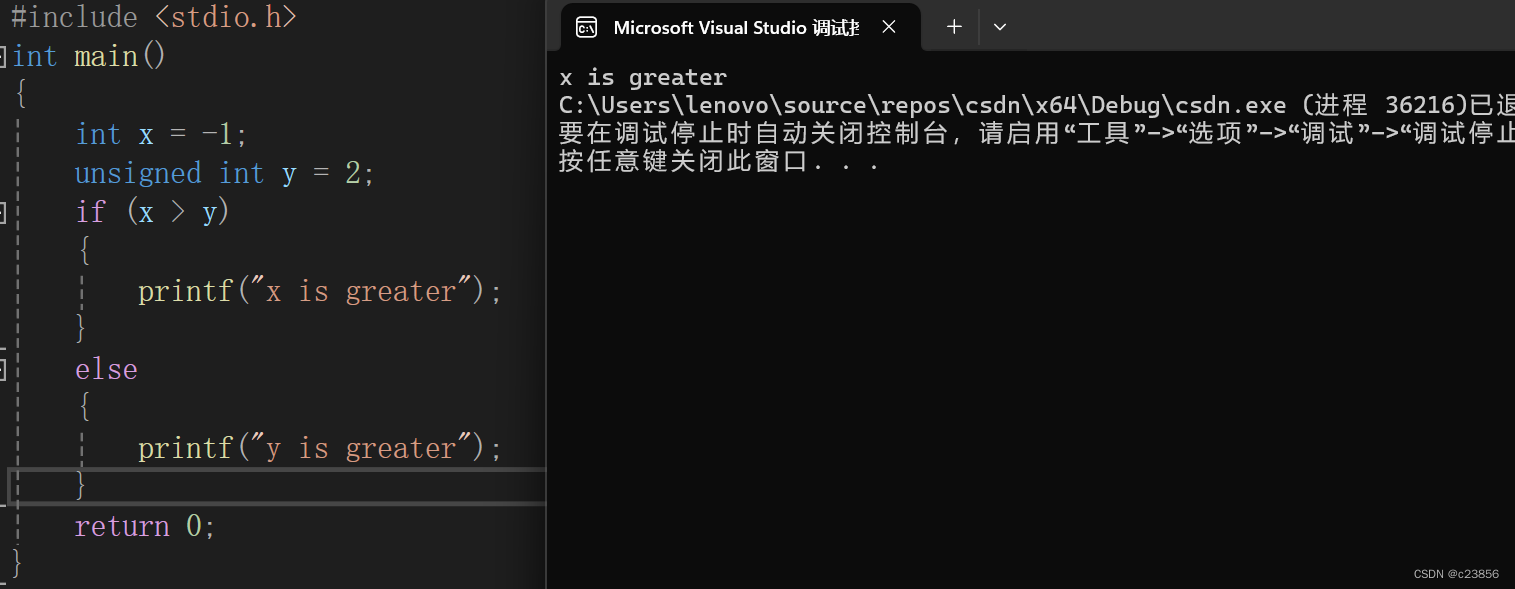
}上述代码运行结果会是什么呢?
我们来分析一下:首先我们创建了一个有符号的整型x,和一个无符号整型y,x是有符号数-1,内存中是全1,当有符号的x和无符号数进行比较时,x会隐式类型转换被当做无符号数,是一个很大的数,所以此时第一个if条件成立,结果应该是打印x is greater,我们运行看看:
3.题3
int k, a, b;
unsigned int w = 5;
double x = 1.42;
我们定义了上述数据类型,下列哪一个选项不符合c语言语法表达式:
A: x%3 B: w+=-20 C: k=(a=200,b=300) D: a+=a-=a=9
我们来分析一下:A选项其实很明显,%取模操作符的两个操作数必须为整数,而在上述类型中x是double类型得数据,故A错误。C选项其实是一个逗号表达式,其表达式的最终结果为最后一个表达式的结果。
4.题4
void func()
{
int k = 1^(1 << 31 >> 31);
printf("%d\n", k);
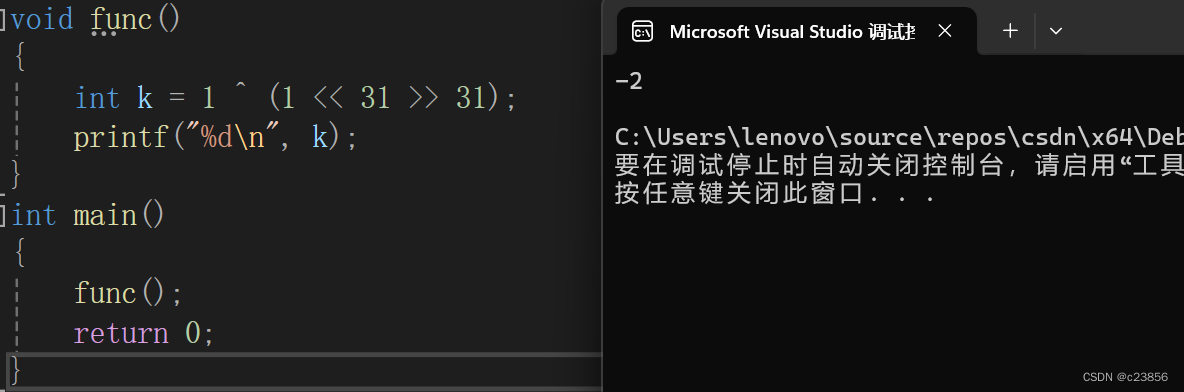
}上述代码的运行结果是什么?
我们来分析一下:我们知道^操作符的运算规则为,相同为0,相异为1。首先()的优先级最高所以先计算()里面的表达式,1<<31,后1的补码变为10000000000000000000000000000000
然后该补码又进行>>31,结果变为11111111111111111111111111111111,最后进行^操作后补码为
11111111111111111111111111111110,这里是补码·,我们将它还原为原码为10000000000000000000000000000010,这时的结果就为-2。所以其运行结果应该为-2,我们运行看看:
5.题5
给你一个含 n 个整数的数组 nums ,其中 nums[i] 在区间 [1, n] 内。请你找出所有在 [1, n] 范围内但没有出 现在 nums 中的数字,并以数组的形式返回结果。
int* findDisappearedNumbers(int* nums, int numsSize, int* returnSize){
for (int i = 0; i < numsSize; i++) {
if (nums[abs(nums[i]) - 1] > 0)
nums[abs(nums[i]) - 1] = -(nums[abs(nums[i]) - 1]);
}
int *ret = (int *)malloc(sizeof(int) * (numsSize));
*returnSize = 0;
for (int i = 0; i < numsSize; i++) {
if (nums[i] > 0) {
ret[*returnSize] = i + 1;
*returnSize += 1;
}
}
return ret;
}还是那句话,勤动脑,多动手。大家要勇于尝试,加油!祝大家都早日成为大佬。

相关文章:

c语言经典测试题8
在c语言经典测试题6的第一题,大家是否想过可不可以将递归参数改为s呢?或许有的人已经试过了,但是发现好像不会有结果,其实是因为s为后置,先试用后加1,然而我们这个是在s出了函数之后才会运行加1操作&#x…...

解决GitHub无法访问的问题:手动修改hosts文件与使用SwitchHosts工具
✨✨ 欢迎大家来访Srlua的博文(づ ̄3 ̄)づ╭❤~✨✨ 🌟🌟 欢迎各位亲爱的读者,感谢你们抽出宝贵的时间来阅读我的文章。 我是Srlua,在这里我会分享我的知识和经验。&#x…...
ETL数据仓库的使用方式
一、ETL的过程 在 ETL 过程中,数据从源系统中抽取(Extract),经过各种转换(Transform)操作,最后加载(Load)到目标数据仓库中。以下是 ETL 数仓流程的基本步骤:…...

POST参数里加号+变成空格的问题处理
今天遇到个这样的问题,从前端传到后端的加密报文,里面包含了号,但在后端日志输出看出,变成空格。这个是由于经过RSA加密后引起的 解决办法: 1.前端转码:使用encodeURIComponent对参数进行转码 2.后端解码…...

【华为面试基础题】检查是否存在满足条件的数字组合
描述 给定一个正整数数组检查数组中是否存在满足规则的数组组合 规则: AB2C 输入描述: 第一行输出数组的元素个数,接下来一行输出所有数组元素,用空格隔开 输出描述: 如果存在满足要求的数 在同一行里依次输出 规则…...
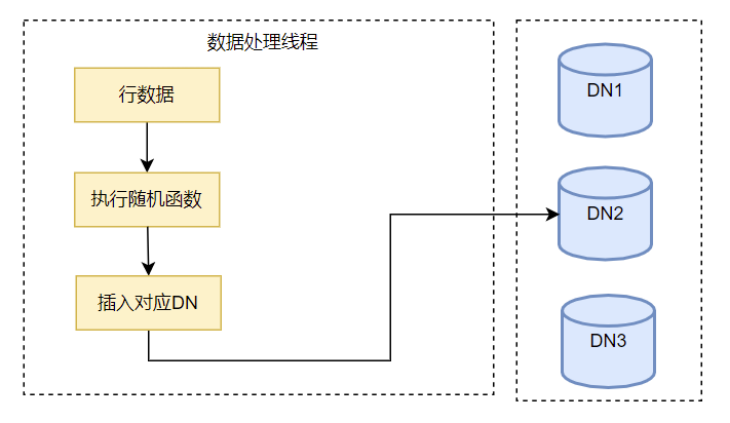
亚信安慧AntDB数据并行加载工具的实现(一)
1.概述 数据加载速度是评判数据库性能的重要指标,能否提高数据加载速度,对文件数据进行并行解析,直接影响数据库运维管理效率。基于此,AntDB分布式数据库提供了两种数据加载方式: 一是类似于PostgreSQL的Copy命令&am…...

面经 | Java创建线程的三种方式
利用JUC包创建线程的三种方式: 通过继承Thread类创建线程类实现Runnable接口创建线程类通过Callable和Future接口创建线程 继承Thread类创建线程 class Thread1 extends Thread {Overridepublic void run() {System.out.println("启动线程1");} }实现R…...

【计算机网络】五种IO模型与IO多路转接之select
文章目录 一、五种IO模型二、非阻塞IO1.fcntl2.实现函数SetNoBlock3.轮询方式读取标准输入 三、I/O多路转接之select1.初识select2.select函数原型3.socket就绪条件4.select的特点5.select缺点6.select使用案例--只读取数据的server服务器1.err.hpp2.log.hpp3.sock.hpp4.select…...

通过一篇文章让你了解数据结构和算法的重要性
通过一篇文章让你了解数据结构和算法的重要性 前言一、 什么是数据结构?二、什么是算法?三、数据结构和算法的重要性在校园招聘的笔试中:在校园招聘的面试中:在未来的工作中: 四、如何学好数据结构和算法4.1 死磕代码&…...

python代码优化学习
代码优化对比: 优化前: # 登录系统 xxljob_login() start_time time.time() # 循环处理需要补数的数据 for item in authId_lists: preSettleInfoHandler(item) count 1 print("运行了第" str(count) "个") …...

C#,数值计算,求解微分方程的吉尔(Gear)四阶方法与源代码
1 微分方程 微分方程,是指含有未知函数及其导数的关系式。解微分方程就是找出未知函数。 微分方程是伴随着微积分学一起发展起来的。微积分学的奠基人Newton和Leibniz的著作中都处理过与微分方程有关的问题。微分方程的应用十分广泛,可以解决许多与导数…...

2024年新提出的算法|LEA爱情进化算法(Love Evolution Algorithm)
Love Evolution Algorithm: a stimulus–value–role theory-inspired evolutionary algorithm for global optimization 爱情进化算法Love Evolution Algorithm,LEA,于2024年2月发表在中科院3区SCI期刊 The Journal of Supercomputing。 1、简介 本文提…...

javaWeb个人学习02
会话技术 会话: 用户打开浏览器,访问web服务器的资源,会话建立,直到有一方断开连接,会话结束.在一次会话中包含多次请求和响应 会话跟踪: 一种维护浏览器状态的方法,服务器需要识别多次请求是否来自于同一个浏览器,以便在同一次会话的多次请求之间共享数据 会话跟踪方案: …...

EchoServer回显服务器封装与测试
目录 类实现 编译测试 这一篇本质上是为了TcpServer而做的一层封装,让外界调用更加简洁 参考上文 TcpServer服务器管理模块(模块十)-CSDN博客 类实现 echo.hpp #include "../server.hpp"class EchoServer { private:TcpServer _server;private:void OnConnect…...

详解POCV/SOCV的时序报告
POCV/SOCV的时序报告中有如下变量: Mean: 高斯分布中的μ值(平均值) Sensit: sensitivity,也就是1个Sigma的值; Corner: Sigma边界的最差值 cell的delay Delay mean N * Delay sigma; cell 的Transition Sl…...
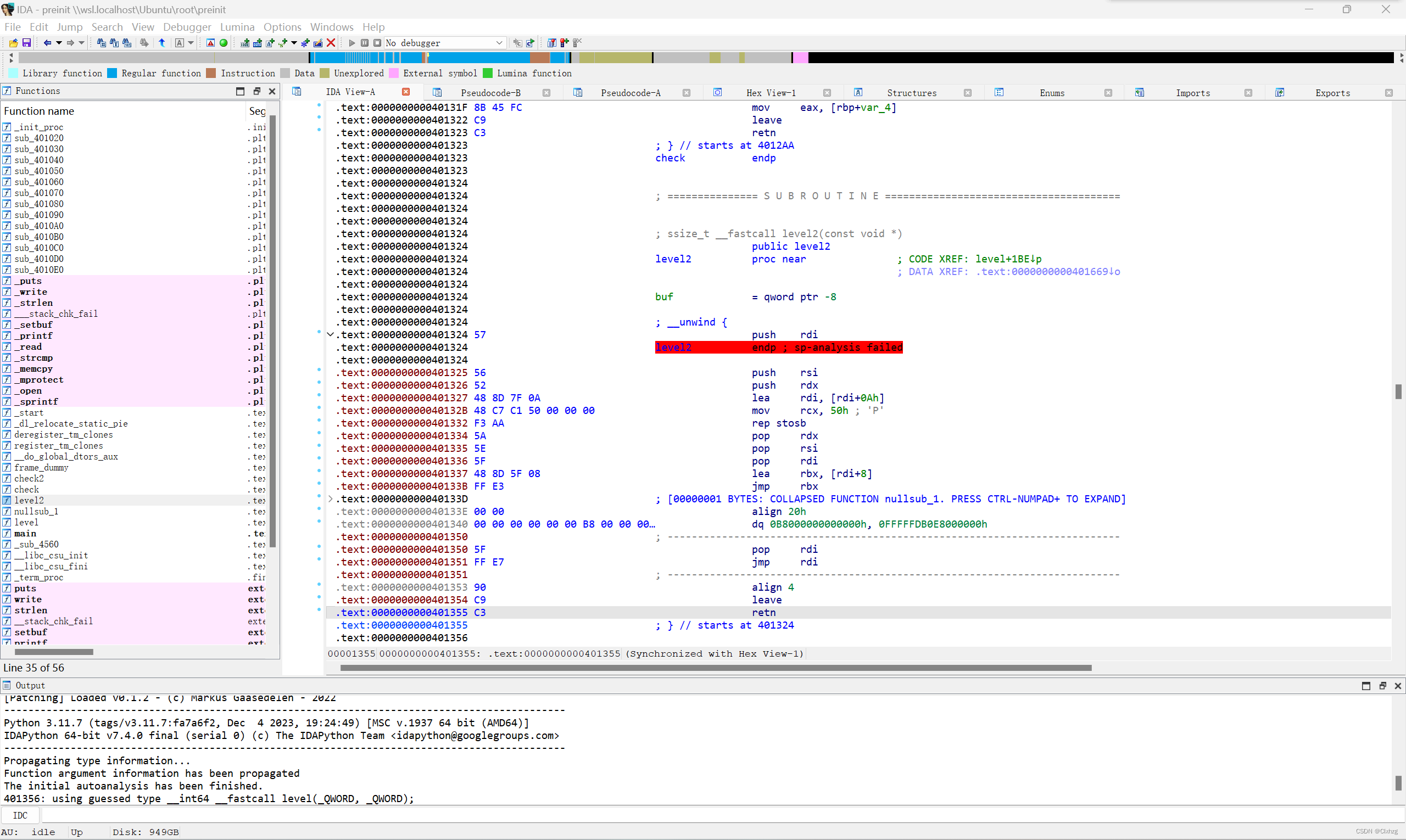
[VNCTF2024]-PWN:preinit解析(逆向花指令,绕过strcmp,函数修改,机器码)
查看保护: 查看ida: 这边其实看反汇编没啥大作用,需要自己动调。 但是前面的绕过strcmp还是要看一下的。 解题: 这里是用linux自带的产生随机数的文件urandom来产生一个随机密码,然后让我们输入密码,用st…...

网络通信技术
▶1.分组交换技术 在网络通信中,数据通过网络节点的某种转发方式,实现从一个端系统到另一个端系统之间的数据传输技术称为数据交换技术。数据交换技术有电路交换、报文交换和分组交换,计算机网络采用分组交换技术。 分组就是源主机(如服务器…...
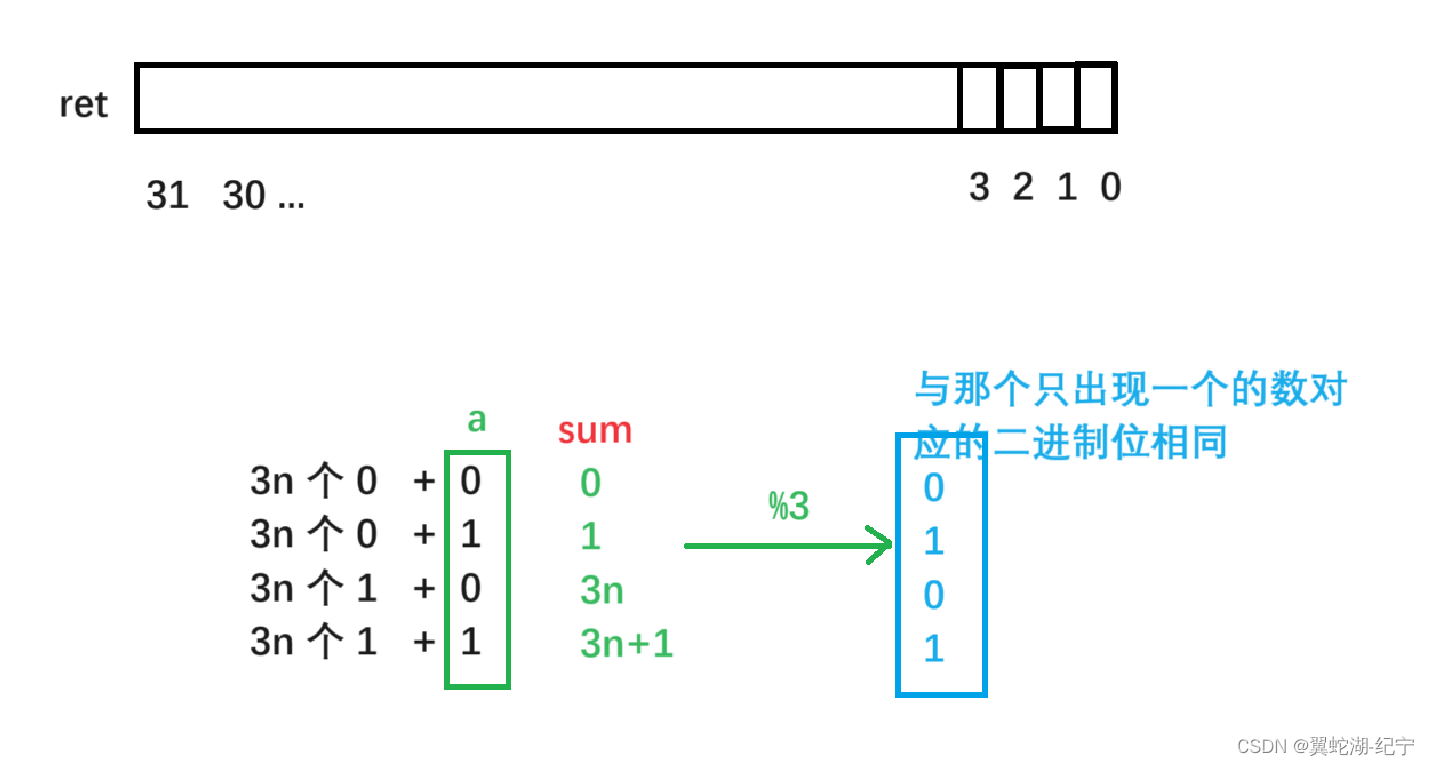
【刷题】位运算
消失的两个数字 消失的两个数字 “单身狗”进阶版思路 class Solution { public:vector<int> missingTwo(vector<int>& nums) {int ret 0;int n nums.size();for(int i 0; i < n; i){ret ^ (nums[i] ^ i);}ret ^ (n ^ (n 1) ^ (n 2));// 按位异或的…...

C++重新入门-string容器
目录 1.包含头文件 2.创建字符串 3.获取字符串长度 4.字符串拼接 5.字符串比较 相等性比较 大小比较 使用比较函数 6.访问字符串 7.查找子串 8.字符串修改 替换子串 插入字符或子串 删除字符或子串 9.提取子串 10.总结 当谈到C中的字符串时,std::str…...

C语言头歌:指针进阶
第1关:输出若干个学生成绩中的最高分.要求用指针函数实现 任务描述 题目描述:读入n(1 < n < 1000)个学生的成绩,成绩都为整数,用指针函数求出若干个学生成绩的最高分。用数组名作为函数参数,指针作为函数返回值。 ####相关…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...
