C#,数值计算,求解微分方程的吉尔(Gear)四阶方法与源代码

1 微分方程
微分方程,是指含有未知函数及其导数的关系式。解微分方程就是找出未知函数。
微分方程是伴随着微积分学一起发展起来的。微积分学的奠基人Newton和Leibniz的著作中都处理过与微分方程有关的问题。微分方程的应用十分广泛,可以解决许多与导数有关的问题。物理中许多涉及变力的运动学、动力学问题,如空气的阻力为速度函数的落体运动等问题,很多可以用微分方程求解。此外,微分方程在化学、工程学、经济学和人口统计等领域都有应用。
数学领域对微分方程的研究着重在几个不同的面向,但大多数都是关心微分方程的解。只有少数简单的微分方程可以求得解析解。不过即使没有找到其解析解,仍然可以确认其解的部分性质。在无法求得解析解时,可以利用数值分析的方式,利用电脑来找到其数值解。 动力系统理论强调对于微分方程系统的量化分析,而许多数值方法可以计算微分方程的数值解,且有一定的准确度。
2 数值解法
作为数值分析的基础内容,常微分方程数值解法的研究已发展得相当成熟,理论上也颇为完善,各类有实用价值的算法已经建立,并已形成计算机软件。它处理问题的思路与方法常可用于偏微分方程的数值求解。主要研究以下三类定解问题的数值解法:初值问题、两点边值问题与特征值问题。初值问题的数值解法应用广泛,是常微分方程数值解法的主要内容。在这方面有突出贡献的学者当推达赫奎斯特(Dahlquist,G.)、巴特赫尔(Butcher,J.C.)及吉尔(Gear,C.W.)等人。两点边值问题及特征值问题的研究相对较为薄弱,其中凯勒尔(Keller,H.B.)的工作影响较大。

Gear, C.William
3 源程序
using System;
using System.Collections;
using System.Collections.Generic;
namespace Legalsoft.Truffer.Algorithm
{
/// <summary>
/// 给定微分方程的一阶偏导方程
/// </summary>
/// <param name="x"></param>
/// <param name="y"></param>
/// <returns></returns>
public delegate double SDE_Equation(double x, double y);
/// <summary>
/// 求解微分方程的吉尔四阶方法
/// C# program to implement Gill's method
/// </summary>
public static partial class Algorithm_Gallery
{
public static SDE_Equation dydx = null;
/// <summary>
/// 求解微分方程的吉尔四阶方法
/// </summary>
/// <param name="x0">起点x坐标</param>
/// <param name="y0">起点y坐标</param>
/// <param name="x">求值点x坐标</param>
/// <param name="step">步长</param>
/// <returns></returns>
public static double SDE_Gill_Method(double x0, double y0, double x, double step)
{
int n = (int)((x - x0) / step);
double y = y0;
for (int i = 1; i <= n; i++)
{
double k1 = step * dydx(x0, y);
double k2 = step * dydx(x0 + 0.5 * step, y + 0.5 * k1);
double k3 = step * dydx(x0 + 0.5 * step, y + 0.5 * (-1 + Math.Sqrt(2)) * k1 + k2 * (1 - 0.5 * Math.Sqrt(2)));
double k4 = step * dydx(x0 + step, y - (0.5 * Math.Sqrt(2)) * k2 + k3 * (1 + 0.5 * Math.Sqrt(2)));
y = y + (1.0 / 6) * (k1 + (2 - Math.Sqrt(2)) * k2 + (2 + Math.Sqrt(2)) * k3 + k4);
x0 = x0 + step;
}
return y;
}
}
}
使用该方法的参考代码(POWER BY 315SOFT.COM):
using Legalsoft.Truffer.Algorithm;
namespace Legalsoft.Drive
{
public partial class Form1 : Form
{
public double func(double x, double y)
{
return x/2 + y*y;
}
private void button1_Click(object sender, EventArgs e)
{
Algorithm_Gallery.dydx = func;
MessageBox.Show("result="+ Algorithm_Gallery.SDE_Gill_Method(0.0,0.0,0.5,30));
}
}
}

4 源代码
using System;
using System.Collections;
using System.Collections.Generic;namespace Legalsoft.Truffer.Algorithm
{/// <summary>/// 给定微分方程的一阶偏导方程/// </summary>/// <param name="x"></param>/// <param name="y"></param>/// <returns></returns>public delegate double SDE_Equation(double x, double y);/// <summary>/// 求解微分方程的吉尔四阶方法/// C# program to implement Gill's method/// </summary>public static partial class Algorithm_Gallery{public static SDE_Equation dydx = null;/// <summary>/// 求解微分方程的吉尔四阶方法/// </summary>/// <param name="x0">起点x坐标</param>/// <param name="y0">起点y坐标</param>/// <param name="x">求值点x坐标</param>/// <param name="step">步长</param>/// <returns></returns>public static double SDE_Gill_Method(double x0, double y0, double x, double step){int n = (int)((x - x0) / step);double y = y0;for (int i = 1; i <= n; i++){double k1 = step * dydx(x0, y);double k2 = step * dydx(x0 + 0.5 * step, y + 0.5 * k1);double k3 = step * dydx(x0 + 0.5 * step, y + 0.5 * (-1 + Math.Sqrt(2)) * k1 + k2 * (1 - 0.5 * Math.Sqrt(2)));double k4 = step * dydx(x0 + step, y - (0.5 * Math.Sqrt(2)) * k2 + k3 * (1 + 0.5 * Math.Sqrt(2)));y = y + (1.0 / 6) * (k1 + (2 - Math.Sqrt(2)) * k2 + (2 + Math.Sqrt(2)) * k3 + k4);x0 = x0 + step;}return y;}}
}相关文章:

C#,数值计算,求解微分方程的吉尔(Gear)四阶方法与源代码
1 微分方程 微分方程,是指含有未知函数及其导数的关系式。解微分方程就是找出未知函数。 微分方程是伴随着微积分学一起发展起来的。微积分学的奠基人Newton和Leibniz的著作中都处理过与微分方程有关的问题。微分方程的应用十分广泛,可以解决许多与导数…...

2024年新提出的算法|LEA爱情进化算法(Love Evolution Algorithm)
Love Evolution Algorithm: a stimulus–value–role theory-inspired evolutionary algorithm for global optimization 爱情进化算法Love Evolution Algorithm,LEA,于2024年2月发表在中科院3区SCI期刊 The Journal of Supercomputing。 1、简介 本文提…...

javaWeb个人学习02
会话技术 会话: 用户打开浏览器,访问web服务器的资源,会话建立,直到有一方断开连接,会话结束.在一次会话中包含多次请求和响应 会话跟踪: 一种维护浏览器状态的方法,服务器需要识别多次请求是否来自于同一个浏览器,以便在同一次会话的多次请求之间共享数据 会话跟踪方案: …...

EchoServer回显服务器封装与测试
目录 类实现 编译测试 这一篇本质上是为了TcpServer而做的一层封装,让外界调用更加简洁 参考上文 TcpServer服务器管理模块(模块十)-CSDN博客 类实现 echo.hpp #include "../server.hpp"class EchoServer { private:TcpServer _server;private:void OnConnect…...

详解POCV/SOCV的时序报告
POCV/SOCV的时序报告中有如下变量: Mean: 高斯分布中的μ值(平均值) Sensit: sensitivity,也就是1个Sigma的值; Corner: Sigma边界的最差值 cell的delay Delay mean N * Delay sigma; cell 的Transition Sl…...
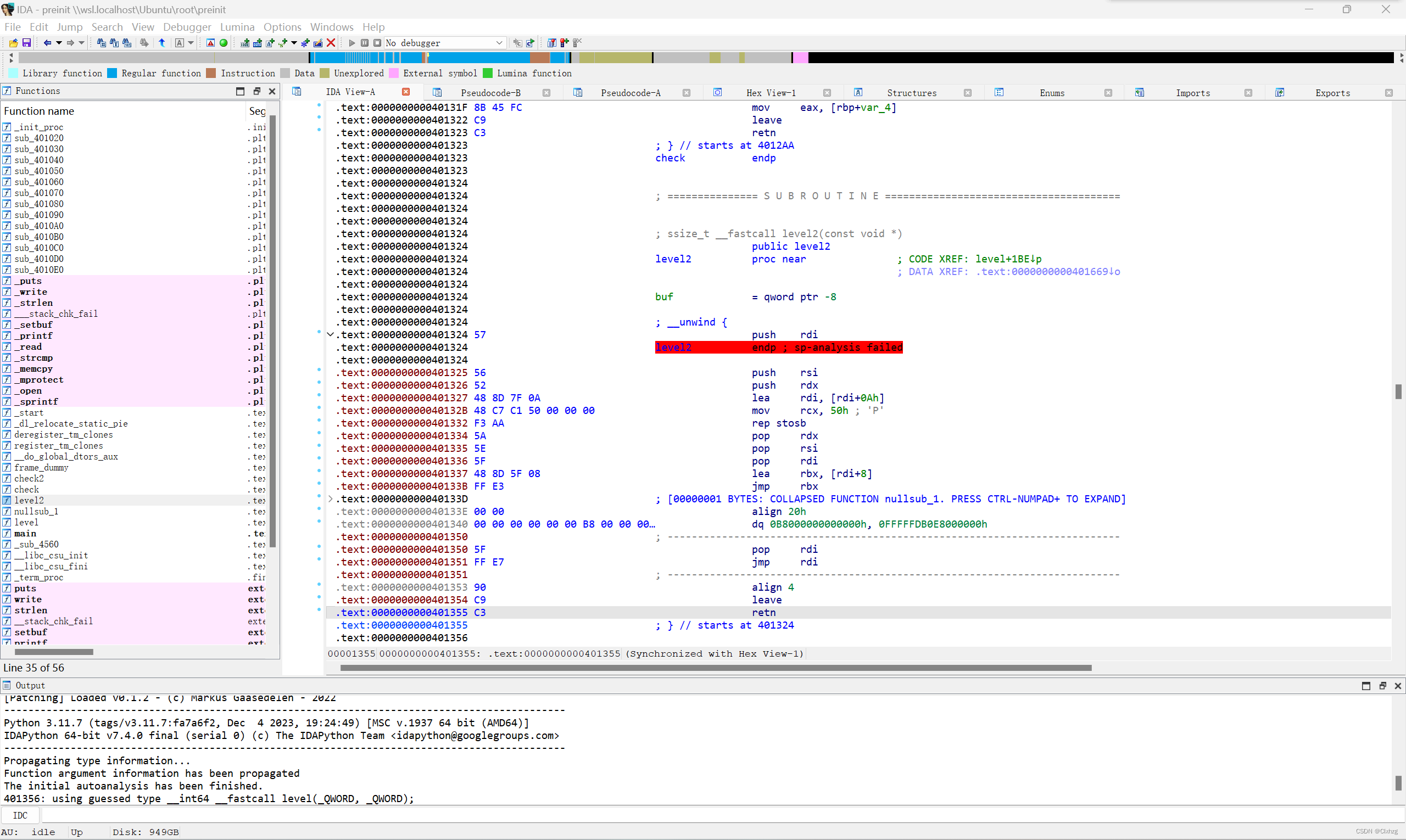
[VNCTF2024]-PWN:preinit解析(逆向花指令,绕过strcmp,函数修改,机器码)
查看保护: 查看ida: 这边其实看反汇编没啥大作用,需要自己动调。 但是前面的绕过strcmp还是要看一下的。 解题: 这里是用linux自带的产生随机数的文件urandom来产生一个随机密码,然后让我们输入密码,用st…...

网络通信技术
▶1.分组交换技术 在网络通信中,数据通过网络节点的某种转发方式,实现从一个端系统到另一个端系统之间的数据传输技术称为数据交换技术。数据交换技术有电路交换、报文交换和分组交换,计算机网络采用分组交换技术。 分组就是源主机(如服务器…...
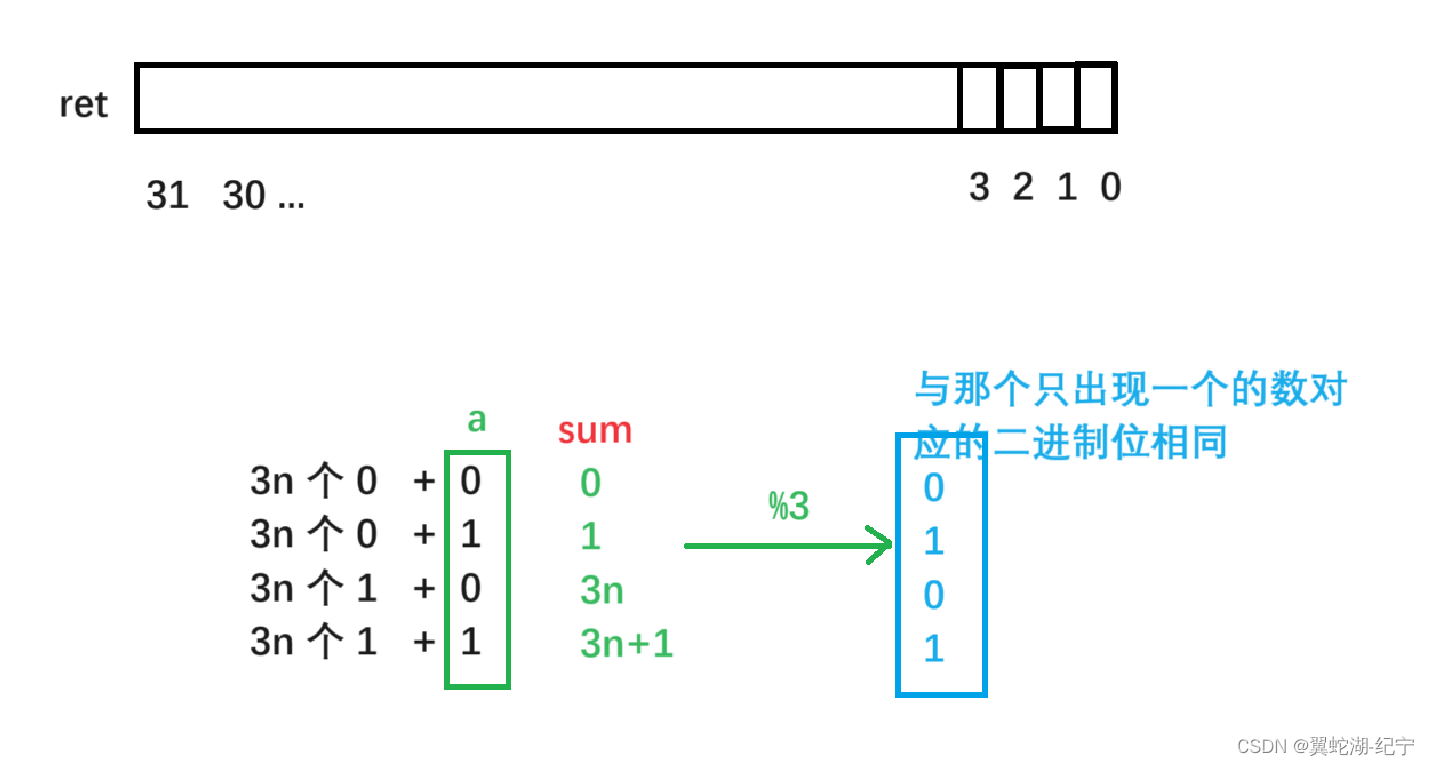
【刷题】位运算
消失的两个数字 消失的两个数字 “单身狗”进阶版思路 class Solution { public:vector<int> missingTwo(vector<int>& nums) {int ret 0;int n nums.size();for(int i 0; i < n; i){ret ^ (nums[i] ^ i);}ret ^ (n ^ (n 1) ^ (n 2));// 按位异或的…...

C++重新入门-string容器
目录 1.包含头文件 2.创建字符串 3.获取字符串长度 4.字符串拼接 5.字符串比较 相等性比较 大小比较 使用比较函数 6.访问字符串 7.查找子串 8.字符串修改 替换子串 插入字符或子串 删除字符或子串 9.提取子串 10.总结 当谈到C中的字符串时,std::str…...

C语言头歌:指针进阶
第1关:输出若干个学生成绩中的最高分.要求用指针函数实现 任务描述 题目描述:读入n(1 < n < 1000)个学生的成绩,成绩都为整数,用指针函数求出若干个学生成绩的最高分。用数组名作为函数参数,指针作为函数返回值。 ####相关…...

【C++】一个求数组中最大元素的函数模板
题目 设计一个分数类 F r a c t i o n Fraction Fraction,再设计一个名为 M a x e l e m e n t Max_element Maxelement 的函数模板,能够求数组中最大的元素,并用该模板求一个 F r a c t i o n Fraction Fraction 数组中的最大元素。 C…...

SpringCloud Alibaba(保姆级入门及操作)
第一章 微服务概念 1.0 科普一些术语 科普一下项目开发过程中常出现的术语,方便后续内容的理解。 **服务器:**分软件与硬件,软件:类型tomcat这种跑项目的程序, 硬件:用来部署项目的电脑(一般性能比个人电脑好) **服务:**操作系统上术语:一个程序,开发中术语:一个…...

SpringBoot集成Activiti案例
前言 Activiti项目是一项新的基于Apache许可的开源BPM平台,从基础开始构建,旨在提供支持新的BPMN 2.0标准,包括支持对象管理组(OMG),面对新技术的机遇,诸如互操作性和云架构,提供技…...
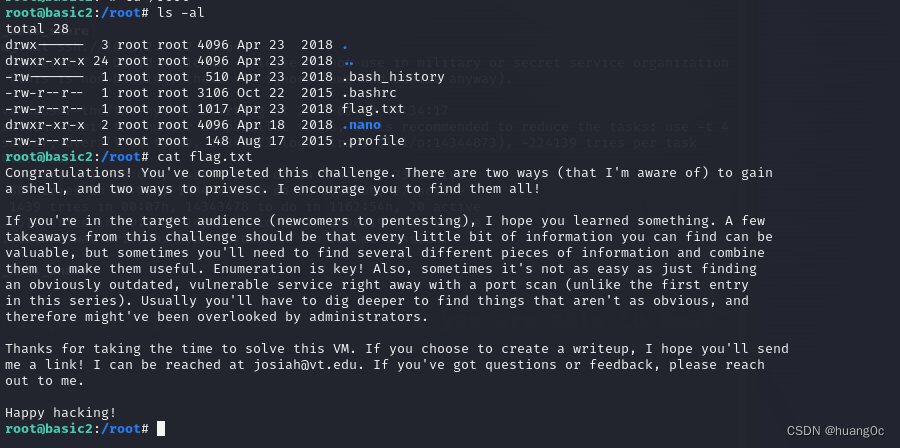
Vulnhub靶机:basic_pentesting_2
一、介绍 运行环境:Virtualbox 攻击机:kali(10.0.2.4) 靶机:basic_pentesting_2(10.0.2.7) 目标:获取靶机root权限和flag 靶机下载地址:https://download.vulnhub.c…...

复试PAT乙级day33
PAT乙级1106~1110 1106_2019数列有一个测试点过不了 1109_擅长C 这题不会,通过的是别人的代码 1110_区块反转 这题跟1105_链表合并 的处理很像。值得注意的是分段区间翻转用 大转小转 的方式。这题也有一个测试点通不过。...

npm ERR! path /Users/apple/.npm/_cacache/index-v5/11/77/cf18d9ab54d565b57fb3
在使用npm时,有时候您可能会遇到类似以下错误的权限问题: npm ERR! path /Users/apple/.npm/_cacache/index-v5/11/77/cf18d9ab54d565b57fb3 npm ERR! code EACCES npm ERR! errno -13 npm ERR! syscall open npm ERR! Error: EACCES: permission denie…...

震惊!python类型的自动化测试框架原来这么简单!
自2018年被评选为编程语言以来,Python在各大排行榜上一直都是名列前茅。目前,它在Tiobe指数中排名第三个,仅次于Java和C。随着该编程语言的广泛使用,基于Python的自动化测试框架也应运而生,且不断发展与丰富。 因此&am…...
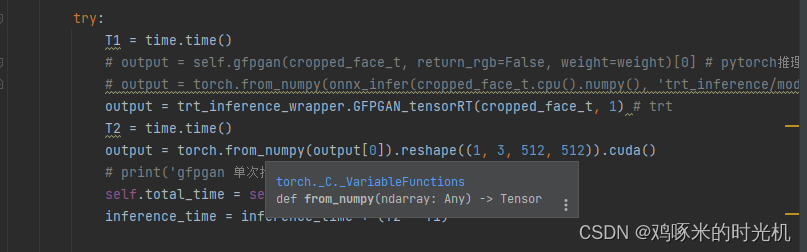
人脸高清算法GFPGAN之TensorRT推理
1. 综述 最近由于做数字人项目,采用的是wav2lip GFPGAN进行人脸面部高清,但GFPGAN模型本身比较大,所以想着使用TensorRT来代替原始的pth推理看看能否提升运行速度,于是便开始了这趟windows1之下进行GFPGAN的trt推理的折腾之旅。…...

05 OpenCV图像混合技术
文章目录 理论算子示例 理论 其中 的取值范围为0~1之间 算子 addWeighted CV_EXPORTS_W void addWeighted(InputArray src1, double alpha, InputArray src2, double beta,double gamma, OutputArray dst, int dtype -1 ); 参数1:输入图像Mat …...
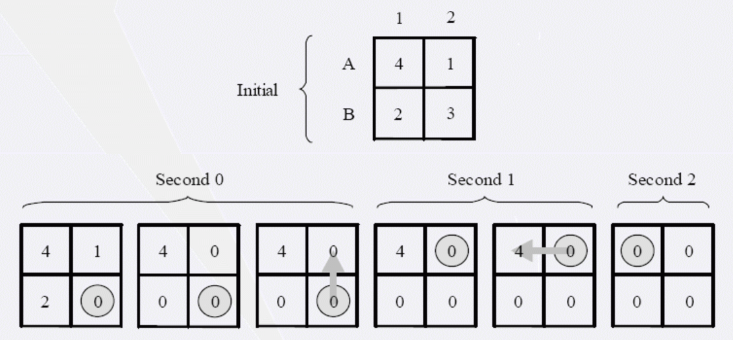
2326. 王者之剑(网络流,最小割,最大权独立集,最小点权覆盖)
活动 - AcWing 给出一个 nm 网格,每个格子上有一个价值 vi,j 的宝石。 Amber 可以自己决定起点,开始时刻为第 0 秒。 以下操作,在每秒内按顺序执行。 若第 i 秒开始时,Amber 在 (x,y),则 Amber 可以拿走 (x,y) 上的…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
