2326. 王者之剑(网络流,最小割,最大权独立集,最小点权覆盖)
活动 - AcWing
给出一个 n×m 网格,每个格子上有一个价值 vi,j 的宝石。
Amber 可以自己决定起点,开始时刻为第 0 秒。
以下操作,在每秒内按顺序执行。
- 若第 i 秒开始时,Amber 在 (x,y),则 Amber 可以拿走 (x,y) 上的宝石。
- 在偶数秒时(i 为偶数),则 Amber 周围 4 格的宝石将会消失。
- 若第 i 秒开始时,Amber 在 (x,y),则在第 (i+1) 秒开始前,Amber 可以马上移动到相邻的格子 (x+1,y),(x−1,y),(x,y+1),(x,y−1) 或原地不动 (x,y)。
求 Amber 最多能得到多大总价值的宝石。
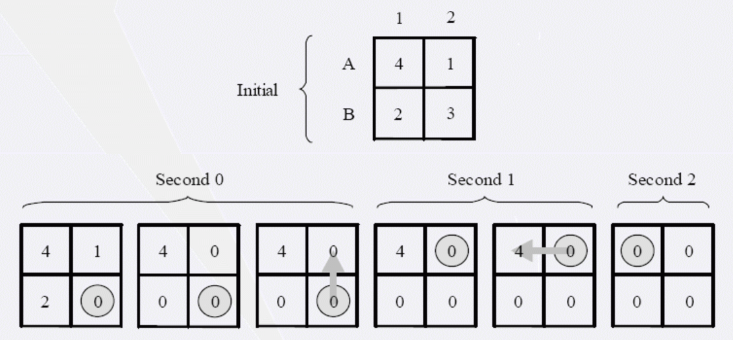
上图给出了一个 2×2 的网格的例子。
在第 0 秒,首先选择 B2 进入,取走宝石 3;由于是偶数秒,周围的格子 A2,B1 的宝石 1,2 消失;向 A2 走去。
在第 1 秒,由于 A2 的宝石已消失,无宝石可取;向 A1 走去。
在第 2 秒,取走 A1 的宝石 4。
全程共取得 2 块宝石:宝石 3 和宝石 4。
输入格式
第一行包含两个整数 n,m。
接下来 n 行,每行包含 m 个整数,用来描述宝石价值矩阵。其中第 i 行第 j 列的整数表示 vi,j。
输出格式
输出可拿走的宝石最大总价值。
数据范围
1≤n,m≤100
1≤vi,j≤1000
输入样例:
2 2
1 2
2 1
输出样例:
4解析:
最大权独立集=总权值 - 最小权点覆盖
性质:
(1)只能在偶数秒拿宝石
(2)不可能拿走相邻格子上的宝石
如果将相邻两个格子之间都连一条边,则能拿的宝石一定是一个独立集。而每个格子上都有一个权值,又是求获得宝石的最大值,可以发现本题已经非常像最大权独立集问题。
到此已经能将任意一个合法方案对应到二分图中的一个独立集。但是还需要证明任意一个二分图中的独立集都能对应到一个合法方案。其实对于任意一个独立集都能构造出一个合法方案,可以从最左上角的一个有宝石的格子开始走,依次去取别的宝石,假设当前距离下一个宝石还剩两步,停下来判断一下,如果当前是偶数秒,直接走过去拿宝石,如果当前是奇数秒,原地停一秒再走过去拿宝石。且保证每次都优先取最近的宝石。这样的行走方案一定能将独立集中的所有宝石拿走,可以自行按照以上思路证明,这里的构造方式非常多,只要掌握好停顿一秒的精髓就能随便构造。
由此得出任意一个合法方案和任意一个独立集都是一一对应的,因此要想求最大能取的宝石价值就等价于求最大权独立集,而最大权独立集 = 总权值 − 最小权点覆盖集。
最大权点独立集的相关概念
独立集: 给定一个一般图 G(V,E),选出图中的某一个点集,使得选出的所有点之间不存在边,则将这个点集称为原图的 独立集
-------------------------------------------------------------------------------------------------------------------
最大权独立集: 给定一个有向图 G(V,E),每个点上有一个非负权值,而图中权值和最大的独立集称为 最大权独立集
-------------------------------------------------------------------------------------------------------------------
如何求最大权独立集:
最大权独立集和最小权点覆盖集问题一样,在一般情况下都是一个 NP 完全问题(NPC 问题),只能用爆搜来解决,但是在二分图中却具有非常高效的特殊做法。
结论:最大权点独立集 = 所有点的总权值 − 最小权点覆盖集
若整个点集是 V,点覆盖集是 V1,那么补集就是 V2=V−V1。
这里有一个性质,任意一个点覆盖集的补集都一定是独立集。这里进一步证明这个性质。可以用反证法,假设点覆盖集 V1 的补集 V2 不是独立集,说明 V2 中存在两个点 u,v 之间存在一条边 (u,v)。由于 V1 同样是 V2 的补集,说明 V1 中一定不包含 u,v 这两个点,那么 (u,v) 这条边的两个点就都不在 V1 中,即 V1 不是一个点覆盖集,与条件矛盾,反证得出任意一个点覆盖集的补集都是一个独立集。
以上性质反过来,任意一个独立集的补集都一定是点覆盖集。同样用反证法,假设独立集 V2 的补集 V1 不是点覆盖集,就必然存在一条边 (u,v),使得这条边的两个点 u,v 都不在 V1,即一定在 V2 中,也就说明 V2 中存在两个点 u,v 之间是有边的,所以 V2 就不是一个独立集,反证得出任意一个独立集的补集都是一个点覆盖集。
可以发现独立集和点覆盖集之间是存在补集这样一个对应关系的,然后看一下两者之间的数量关系,数量关系就非常明显了,因为 V1 和 V2 互为补集,所以两个集合的权值总和就等于所有点的权值和,即 w(V1)+w(V2)=w(V),而 w(V) 是一个固定值,因此想让 w(V2) 取最大,w(V1) 就必然取到最小,因此要想求最大全独立集,只需要求一下最小权点覆盖集,最小权点覆盖集的补集就是最大权独立集,由此得证结论。
——————————————————————————————————————
作者:小小_88
链接:https://www.acwing.com/file_system/file/content/whole/index/content/6381812/
来源:AcWing
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。(非常棒的作者,建议看原题解)
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
#include<unordered_map>
#include<unordered_set>
#include<bitset>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
const int N = 1e4 + 10, M = (2e4 + N ) * 2 + 10, INF = 0x3f3f3f3f;
int n, m, S, T;
int h[N], e[M], f[M], ne[M], idx;
int q[N], d[N], cur[N];int get(int a, int b) {return (a - 1) * m + b;
}void add(int a, int b, int c) {e[idx] = b, f[idx] = c, ne[idx] = h[a], h[a] = idx++;e[idx] = a, f[idx] = 0, ne[idx] = h[b], h[b] = idx++;
}bool bfs() {int hh = 0, tt = 0;memset(d, -1, sizeof d);q[0] = S, d[S] = 0, cur[S] = h[S];while (hh <= tt) {int t = q[hh++];for (int i = h[t]; i != -1; i = ne[i]) {int j = e[i];if (d[j] == -1 && f[i]) {d[j] = d[t] + 1;cur[j] = h[j];if (j == T)return 1;q[++tt] = j;}}}return 0;
}int find(int u, int limit) {if (u == T)return limit;int flow = 0;for (int i = cur[u]; i != -1 && flow < limit; i = ne[i]) {int j = e[i];cur[u] = i;if (d[j] == d[u] + 1 && f[i]) {int t = find(j, min(f[i], limit - flow));if (!t)d[j] = -1;f[i] -= t, f[i ^ 1] += t, flow += t;}}return flow;
}int dinic() {int ret = 0, flow;while (bfs())while (flow = find(S, INF))ret += flow;return ret;
}int main() {int dx[] = { 0,0,1,-1 }, dy[] = { 1,-1,0,0 };cin >> n >> m;S = 0, T = m * n + 1;memset(h, -1, sizeof h);int tot = 0;for (int i = 1; i <= n; i++) {for (int j = 1,a; j <= m; j++) {scanf("%d", &a);if (i + j & 1) {add(S, get(i, j), a);for (int k = 0; k < 4; k++) {int x = i + dx[k], y = j + dy[k];if (x > 0 && x <= n && y > 0 && y <= m)add(get(i, j), get(x, y), INF);}}else add(get(i, j), T, a);tot += a;}}printf("%d\n", tot - dinic());return 0;
}
相关文章:

2326. 王者之剑(网络流,最小割,最大权独立集,最小点权覆盖)
活动 - AcWing 给出一个 nm 网格,每个格子上有一个价值 vi,j 的宝石。 Amber 可以自己决定起点,开始时刻为第 0 秒。 以下操作,在每秒内按顺序执行。 若第 i 秒开始时,Amber 在 (x,y),则 Amber 可以拿走 (x,y) 上的…...
内网信息搜集
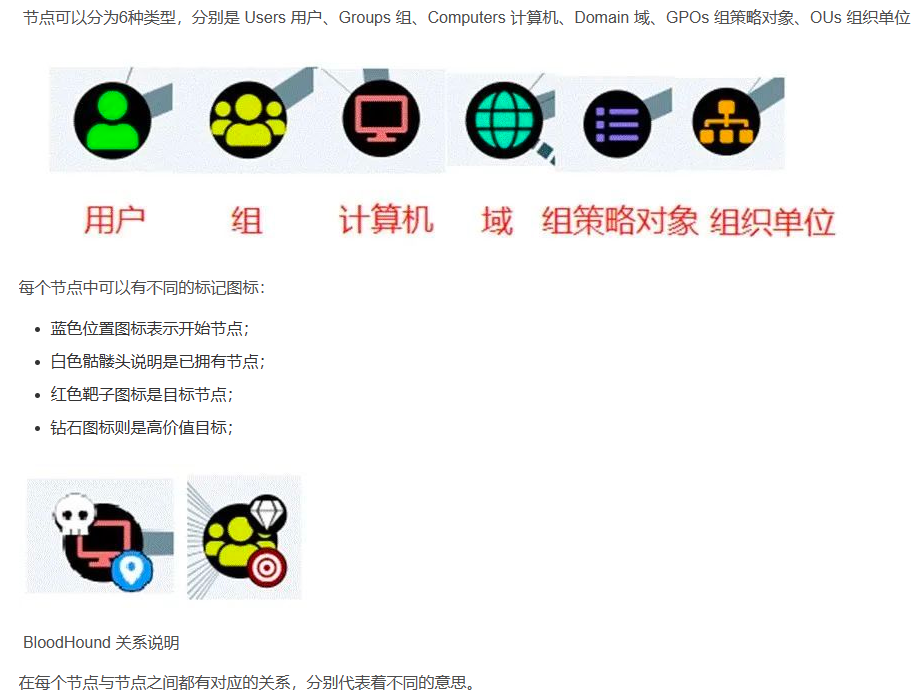
目录 内网基础知识 基本流程图 怎么判断是否在域内 常规信息类收集-应用&服务&权限等 cs信息搜集 bloodhound安装及使用 内网基础知识 工作组:将不同的计算机按照功能分别列入不同的组,想要访问某个部门的资源,只要在【网络】里…...

微型力量,巨大作用:嵌入式技术的创新应用
微型力量,巨大作用:嵌入式技术的创新应用 嵌入式技术是一种将计算机技术嵌入到各种设备和系统中的技术,它的应用范围非常广泛,包括但不限于智能手机、智能家居、医疗设备、工业自动化等领域。这种微型的技术在各个领域中发挥着巨…...
华为 OD 一面算法原题
2.2 亿彩票公布调查结果 昨天,闹得沸沸扬扬的《10 万中 2.2 亿》的彩票事件,迎来了官方公告。 简单来说,调查结果就是:一切正常,合规合法。 关于福利彩票事件,之前的推文我们已经分析过。 甚至在后面出现《…...
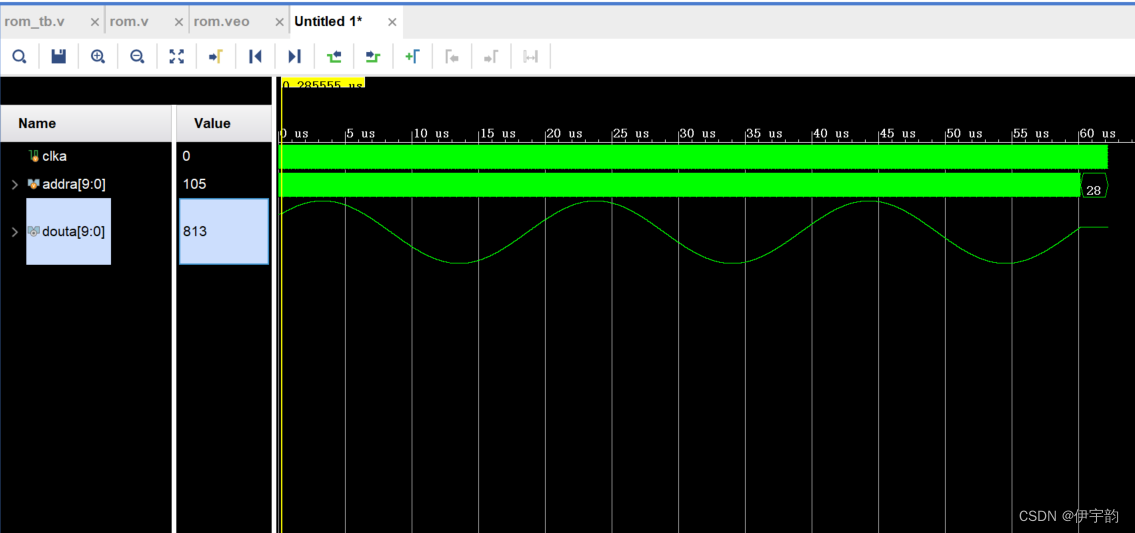
FPGA-学会使用vivado中的存储器资源ROM(IP核)
问题: 某芯片,有500个寄存器,需要在上电的时候由FPGA向这些寄存器中写入初始值,初始值已经通过相应的文档给出了具体值,这些值都是已知的。 分析关键点: 数据量比较多(Verilog代码,通过case语句、always语句这种查找表的方式,数…...

自测-1 打印沙漏
文章预览: 题目算法代码 题目 算法 以前做过这个,那次是c语言写的,一点一点处理一层一层完成,这次我换了一种语言用了另一种思想使用递归去写,还是我们要先求出应该有多少层这个很容易,中间输出部分我们算…...
)
高级语言期末2009级B卷(计算机学院)
1.编写一个名为mystrcpy的函数,实现将字符串str1的偶数位子的字符的拷贝到另一个字符串str2中。并编写主函数,在主函数中从键盘读入一个长度<100的字符串str1,然后调用函数mystrcpy;最后输出str2,例如,读…...

c# using 用法
using命令空间 导入命名空间中的所有类型 如:using System.Text; using别名 using别名包括详细命名空间信息的具体类型,这种做法有个好处就是当同一个cs引用了两个不同的命名空间,但两个命名空间都包括了一个相同名字的类型的时候。当需要…...

【Django】执行查询—跨关系查询中的跨多值关联问题
跨多值查询 跨越 ManyToManyField 或反查 ForeignKey (例如从 Blog 到 Entry )时,对多个属性进行过滤会产生这样的问题:是否要求每个属性都在同一个相关对象中重合。 filter() 先看filter(),通过一个例子看…...

Spring八股 常见面试题
什么是Spring Bean 简单来说,Bean 代指的就是那些被 IoC 容器所管理的对象。我们需要告诉 IoC 容器帮助我们管理哪些对象,这个是通过配置元数据来定义的。配置元数据可以是 XML 文件、注解或者 Java 配置类。 将一个类声明为 Bean 的注解有哪些? Com…...

今年面试潮,说实话这个开发岗能不能冲?
自打华为 2019 年发布鸿蒙操作系统以来,网上各种声音百家争鸣。尤其是 2023 年发布会公布的鸿蒙 4.0 宣称不再支持 Android,更激烈的讨论随之而来。 当下移动端两大巨头瓜分了绝大部分市场: iOS 是闭源的,只有唯一的一家厂商&am…...
【前端素材】推荐优质在线花卉商城电商网页Flowery平台模板(附源码)
一、需求分析 1、系统定义 在线花卉商城是一个通过互联网提供花卉销售服务的电子商务平台,用户可以在该平台上浏览、选择和购买各种花卉产品。 2、功能需求 在线花卉商城是一个通过互联网提供花卉销售服务的电子商务平台,用户可以在该平台上浏览、选…...
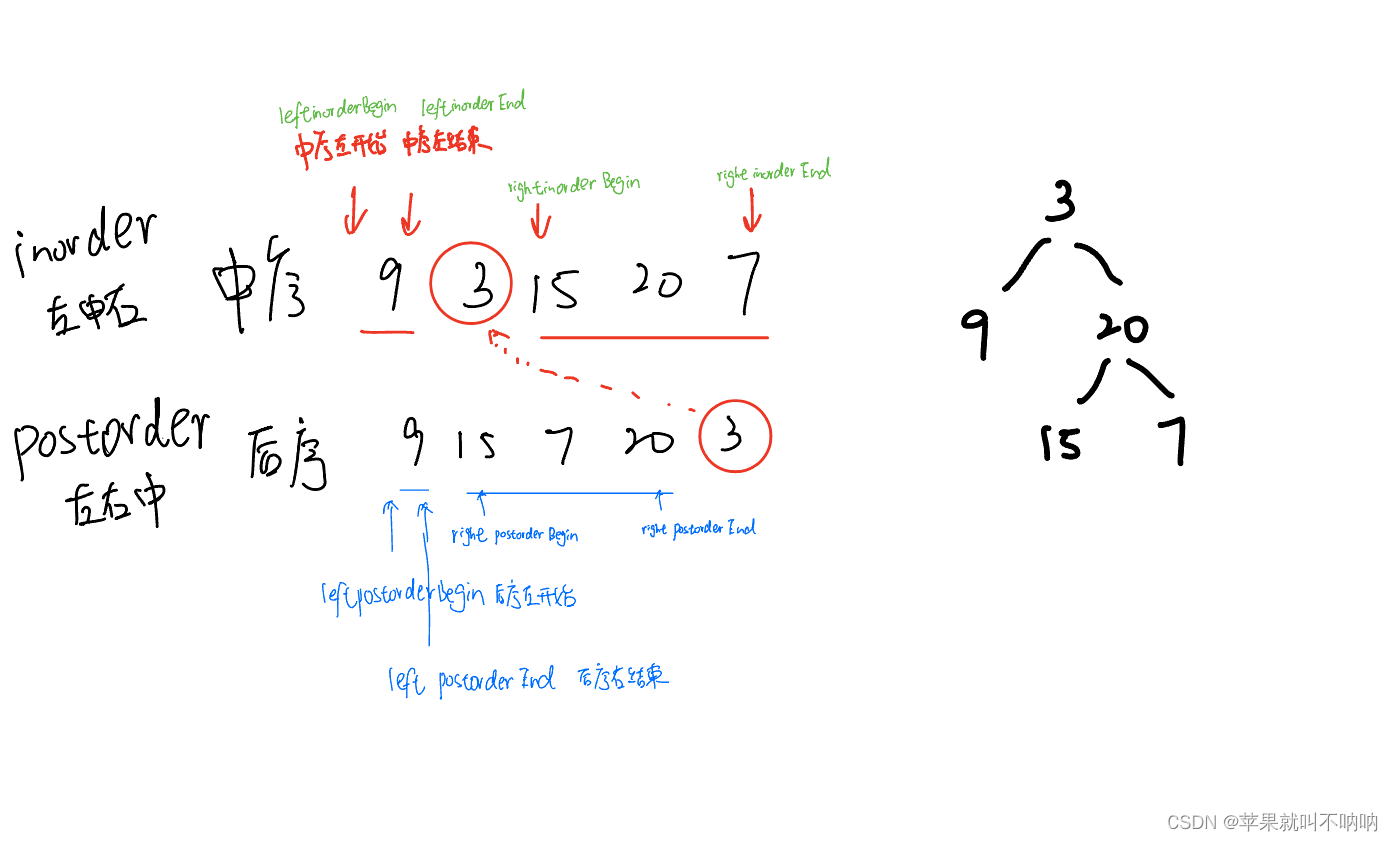
★【递归】【构造二叉树】Leetcode 106.从中序与后序遍历序列构造二叉树
★【递归前序】【构造二叉树】Leetcode 106.从中序与后序遍历序列构造二叉树 105. 从前序与中序遍历序列构造二叉树 106.从中序与后序遍历序列构造二叉树:star:思路分析递归解法 105. 从前序与中序遍历序列构造二叉树递归解法 凡是构造二叉树>>>>>>>>&…...

linux检测和重启python脚本
#!/bin/bash# 检测Flask应用是否挂了 if ! pgrep -f "flask_app.py" >/dev/null; then# 重启Flask应用cd /path/to/your/flask/appnohup python3 flask_app.py >/dev/null 2>&1 & fi这是一个简单的bash脚本,用于检测Flask应用是否挂掉&a…...

HTML+CSS+JS:花瓣登录组件
效果演示 实现了一个具有动态花朵背景和简洁登录框的登录页面效果。 Code <section><img src"./img/background.jpeg" class"background"><div class"login"><h2>Sign In</h2><div class"inputBox"…...

Unity中URP下实现水体(水面反射)
文章目录 前言一、原理1、法一:使用立方体纹理 CubeMap,作为反射纹理使用2、法二:使用反射探针生成环境反射图,所谓反射的采样纹理 二、实现水面反射1、定义和申明CubeMap2、反射向量需要什么3、计算 N ⃗ \vec{N} N 4、计算 V ⃗…...

基于FastJson实现Json数据文件导入导出解析
哈喽,大家好,我是灰小猿,一个超会写bug的程序猿! 今天来记录一个在项目实战中比较实用的方法,主要是针对一些需要存在简单数据文件导入导出的场景,如:数据文件的简单备份、软件升版前后配置导入…...

JVM内存分配与垃圾收集流程
3.8 实战:内存分配与回收策略 3.8.1 对象优先在Eden分配 大多数情况下,对象在新生代Eden区中分配。当Eden区没有足够空间进行分配时,虚拟机将发起一次Minor GC。 3.8.2 大对象直接进入老年代 HotSpot虚拟机提供了-XX:Prete…...

【python】yaml转成json
姊妹篇:【python】json转成成yaml yaml数据: address:city: 北京市postalCode: 100000street: 北京路123号 age: 30 cart: - product:name: 笔记本电脑price: 1199.99quantity: 2 - product:name: 智能手机price: 599.99quantity: 1 children: - age: …...

css5定位
css 一.定位1.概念(定位定位模式边位移)2.静态位移static(不常用)3.相对定位relative(不脱标)(占位置)4.绝对定位absolute(脱标)(不占位置&#x…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...
